Восстановление параметров акустических полей, измеренных волоконной многосенсорной системой, на срезе сопла турбомашины

На практике контроль и измерение пространственных распределений акустических полей на основе волоконно-оптических датчиков различной физической природы осуществляют путем регистрации сигналов от датчиков, размещаемых в совокупности точек контроля [1; 2]. Подобные системы контроля будем называть многоточечными, хотя они могут состоять и из одного датчика, перемещаемого по точкам контроля. Рассмотрим задачу размещения точек контроля и задачу восстановления пространственного распределения поля по измерениям по конечной совокупности точек в отдельности.

Распределенные волоконно-оптические датчики, обеспечивают много преимуществ такие, как высокую чувствительность к изменению физических полей и нечувствительность к электромагнитной интерференции, возможность удаленного зондирования, низкая стоимость и размеры, также их можно использовать в агрессивных средах. Эти преимущества дают основания для применения оптического волокна при использовании его в качестве контролирующего датчика для аэроакусти-ческих измерений на срезе сопла турбомашины и ГТД [3–6].

измерительных линий (рис. 1). Из известных равномерных укладок нами выбраны горизонтальновертикальная и диагональная укладки соответственно для прямоугольного и круглого сопла, как показано в правой части рис. 1.

Для прямоугольных и круглых сопел турбомашин схемам укладки оптических сенсорных волокон, приведенным на рис. 1, присуща «большая ракурсность», то есть множественность числа направлений наблюдений p . Известно [7–10], что в случае полных данных p = 360, то есть когда известны достаточно качественные проекции по всем 360 ракурсам углового диапазона, могут быть получены реконструкции хорошего качества. Для сравнения в медицинской или промышленной томографии для получения качественных изображений необходимое число ракурсов p = 102–103, а для их анализа используются аналитические методы решения уравнений. Поэтому в нашем случае, при значительно превышающей ракурсности стандартные аналитические методы неприемлемы, необходимо решение оптимизации и выбор количества устанавливаемых датчиков.

Так как размещаемые в плоскости среза сопла турбомашины (или иного технического устройства) волоконно-оптические датчики контроля акустического поля могут привести к искажению формы самого поля, это неизбежно приведет и к иск ажению по ля давления. Следовательно, возни-

LM^^e © Виноградов В.Ю., Анфиногентов В.И., 2019

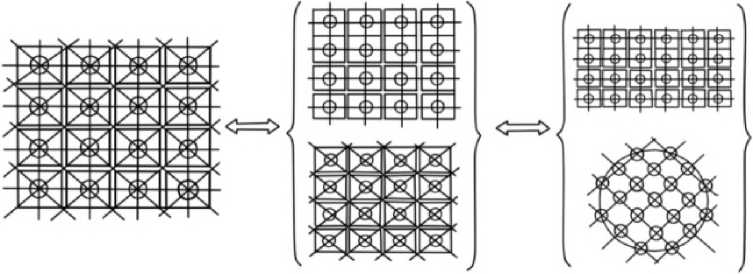
Рис. 1. Выбор схемы укладки измерительных линий волоконно-оптических датчиков для сопел турбомашин прямоугольной и круглой конфигурации

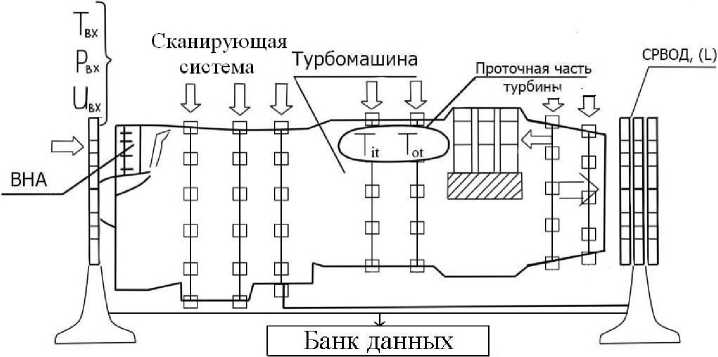
Рис. 2. Автоматизированное диагностическое устройство окружного и построчного контроля акустических параметров на срезе сопла ГТД (СРВОД – система распределенных волоконно-оптических датчиков в соответствии с укладкой по рис. 1)

кает задача размещения минимально возможного числа датчиков контроля для получения заданной точности контроля акустического поля. При этом под контролем будем понимать создание текущего состояния акустического поля в виде непрерывных функций пространственных координат. С этой задачей тесно связана задача осуществления максимально достоверного контроля полей при ограниченном числе датчиков.

Решение задач

Выбирая определенное число точек контроля на периоде самой высокочастотной компоненты в спектре акустического поля, получим общее количество контрольных точек. Однако данный подход к выбору контрольных точек может привести к тому, что общее число точек контроля будет недопустимо большим. В данном разделе для выбора точек контроля предлагаются подходы, основанные на учете более полной априорной информации о подлежащих контролю полях.

Измерительная часть, включающая датчики и блок измерения, предназначена для контроля акустического давления в плоскости среза сопла тур- бомашины или иного технического устройства. Присущие этой плоскости среза сопла размеры и особенности источников возбуждения акустического поля определяют некоторые устойчивые признаки подлежащих контролю полей, что может быть использовано при проектировании системы контроля этих полей, которая представлена на рис. 2.

На каждом цикле измерений поля описываются детерминированными, но заранее неизвестными функциями пространственных координат, изменяющимися от одного цикла измерения к другому. В связи с этим, функцию T ( X ), описывающую зависимость, например, акустического поля от пространственных координат, будем считать реализацией из некоторого статистического ансамбля функций [11].

Изложим предлагаемый подход к проектированию системы контроля для акустического поля.

Зададимся достаточно большим числом базисных функций T ( X ) по различным ракурсам i [12].

Тогда любую реализацию акустического поля по пространственным координатам можно представить с требуемой точностью в виде разложения по базисным функциям:

I

T ( X ) = ^ a i T i ( X ),                                       (1)

i = 1

где a i - коэффициенты, имеющие случайный характер и однозначно определяющие конкретную реализацию акустического поля.

Их статистические характеристики могут быть определены, например, путем цифрового моделирования или экспериментального измерения в лабораторных условиях достаточно полного набора реализаций акустического поля. В дальнейшем предполагается, что a i - центрированные случайные величины, распределенные по нормальному закону с заданной матрицей корреляции R .

Синтез системы контроля пространственного акустического поля включает две основные задачи: определение координат Xm размещения умеренного числа M датчиков и восстановление непрерывной функции T(х) по измеренным значениям поля в разных точках контроля T(Xi), T(X2), ..., T(хм). Восстановление непрерывной реализации акустического поля по значениям в точках контроля сводится к определению по некоторому правилу оценок ai коэффициентов ai. Восста- новленная реализация поля имеет вид:

I

T ( х ) = ^ a i T i ( X ).                                       (2)

i = 1

Точность восстановления акустического поля оценим следующим выражением:

₆ 2 = M         .       ,                                       (3)

MT ( X)||²

где символом M обозначено усреднение по множеству реализаций подлежащих восстановлению полей.

Если функции T i (X ), T 2 ( х ), ..., Tm ( х ) образуют ортонормированную систему функций, то величина 5 ², определяющая близость функций T ( х ) и T ( х ) совпадает с величиной, характеризующей близость коэффициентов a i и a i , так как:

m|t (х) - T (X )|2 = dx =

II

= Ш ^M ^ ^a i T i ( ^X ) - E ^a i T i ( ^X )

Q

= Z ^M l^a i ^-a i |² = M l I^a-a| |².

i = 1

Поэтому точность восстановления акустического поля будем определять выражением:

m| |a-a||

M i a 2

Точность оценки исходного поля зависит от числа и расположения точек контроля х m и от алгоритма определения оценок a i коэффициентов a i . Одновременная оптимизация координат точек контроля и алгоритма вычисления оценок представляет трудноразрешимую проблему, поэтому задачи выбора координат точек контроля и алгоритма вычисления оценок a i коэффициентов a _i будем рассматривать раздельно.

В предположении о том, что известны вероятностные характеристики подлежащих контролю акустических полей, каждой дискретной выборке значений поля в точках контроля может быть поставлено в соответствие количество содержащейся в ней информации. Для нахождения координат точек контроля целесообразно использовать критерий минимума энтропии. Каждой реализации случайного акустического поля T(X) соответствует значение плотности вероятности, характеризующее частоту появления этой реализации. То есть можно говорить о «более вероятных» и «менее вероятных» реализациях. Имея это в виду, задачу восстановления акустического поля T(х) по измеренным в точках контроля значениям можно сформулировать следующим образом: среди всех непрерывных функций T(х), имеющих в точках контроля измеренные значения, найти такую функцию T(х), для которой значение плотности вероятности w (T (X)) будет наибольшим.

Восстановление акустического поля по значениям в контрольных точках является задачей интерполяции непрерывной функции по дискретной выборке. Эта задача решается неоднозначно, что объясняется в частности тем, что по значениям функции T ( х ) в M точках контроля, т. е. по M уравнениям нужно определить коэффициенты i, число которых много больше M. Обычный прием состоит в том, что в разложении (1) сохраняют лишь M базисных функций. При этом вопрос о том, какие из базисных функций выбрать, решается интуитивно.

Даже в рамках такого подхода целесообразно использовать информацию о статистике подлежащих контролю акустических полей, например, в излагаемом ниже варианте,

Среди I базисныхфункций T ( х ), покоторымосу-ществляется разложение акустического поля T ( X ),

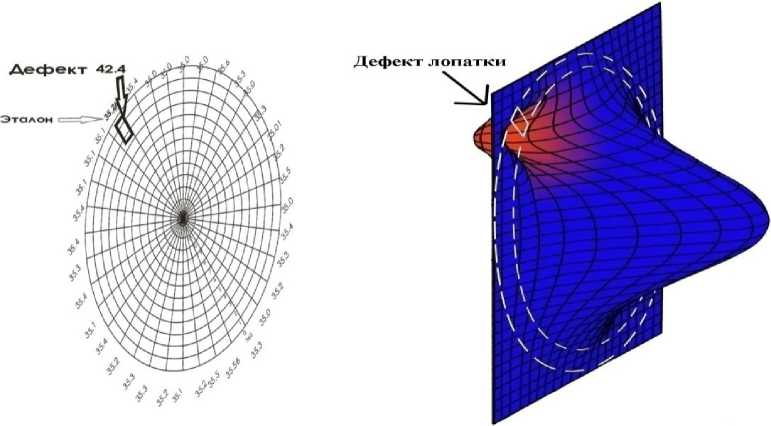
Рис. 3. Результаты визуального представления восстановленного акустического поля с формированием картографического портрета дефекта рабочих лопаток турбомашин в 2D и 3D форматах

выбираются M таких функций, случайные коэффициенты a i при которых имеют наибольшие дисперсии ст 2 , и по результатам измерения акустического поля в дискретном наборе M точек восстанавливаются лишь коэффициенты разложения по выбранным базисным функциям. Таким образом, в данном варианте задача восстановления сводится к решению системы линейных алгебраических уравнений M -го порядка относительно коэффициентов & i :

M

Z & i T im = T m , m = ^ M .                (5)

i = 1

турбомашин разрабатывается для всех типов турбомашин сразу, то в реальных ситуациях, не поддающихся аналитическому расчету, должен быть организован эксперимент по воссозданию рабочих режимов возбуждения акустического поля и проведено измерение совокупности реализаций акустического поля T ( x ) с помощью универсальной измерительной системы (ВСС) с большим числом датчиков. После чего вычисляются необходимые

При этом точность восстановления исходного акустического поля по дискретным значениям характеризуется величиной:

Б ² = 1

—

M ( M

Z 2 Z(T1)

m = 1

mi

T ■ mi

MIM    ²

— ZZZ ( T - ) mi T ст 2 m = 1 j = 1 i = 1

ст:

m

—

I

/ Z ct 2 .

i = 1

Однако использовать имеющуюся априорную информацию можно существенно шире, если из условия оптимизации по какому-либо критерию определять все I коэффициентов.

В завершение необходимо еще раз отметить то обстоятельство, что изложенные выше алгоритмы определения пространственного размещения точек контроля и восстановления акустического поля по дискретным отсчетам основаны на априорной информации о статистике подлежащих восстановлению полей [7–10]. Так как каждая аэроакустическая система контроля параметров

статистические характеристики: математические ожидания и матрица корреляции.

Получены расчетные зависимости дисперсии и погрешности восстановления акустического поля по данным волоконно-оптических измерений.

Число датчиков, обеспечивающее допустимое значение погрешности восстановления акустического поля б ² <  0.01 для значений угла a i равных 15, 45 и 90 ° от вертикали против часовой стрелки, составляет 3, 6 и 8 соответственно. Значения диагональных элементов матрицы R (дисперсия коэффициентов разложения поля излучения F ( ф ) по функциям cos(2 n ф )) проводилось при учете лишь десяти членов ряда. Результаты расчетов показали, что наличие корреляции между коэффициентами разложения акустического поля по функциям cos(2 n ф ) приводит к уменьшению необходимого для достижения заданной точности восстановления числа датчиков. При этом значения дисперсий коэффициентов разложения акустического поля незначительно изменяются при изменении a i .

Для примера на рис. 3 показана визуализация дефекта с ракурсом по углу 15 ° против часовой стрелки от вертикали.

Применение методик восстановления параметров акустических полей с использованием данных волоконно-оптических измерений также было успешно использовано при разработке систем мониторинга вибраций [13], эффективных глушителей для ГТД [14], мобильных комплексов аэроакустической картографии [15] и т. д.

Заключение

Предложена структура аэроакустического комплекса в виде системы автоматического контроля акустических параметров газо-воздушного потока на срезе сопла турбомашины в виде различных по форме измерительных линий волоконно-оптического контроля давления в зависимости от формы контролируемых объектов.

Разработаны и представлены методики восстановления акустического поля, создаваемого газовоздушным потоком турбомашины, реализуемые по данным измерений на выходе СРВОД, с использованием только статистического подхода.

Восстановление поля представлено в виде непрерывных функций пространственных координат, построенных по результатам измерения в дискретной совокупности точек при наличии априорной информации о свойствах измеряемых акустических полей.

Рассмотрены перспективы применения указанных методик и средств для решения близких задач аэроакустической картографии.