Восстановление параметров течения вязкой теплопроводной жидкости по некоторым измерениям на ее поверхности

Рассматривается задача определения температуры и поля скоростей жидкости, движущейся в некоторой области Ω ⊂ R2 , по некоторым заданным условиям на границе области Ω . Математическая модель стационарной тепловой конвекции вязкой несжимаемой неоднородной жидкости включает в себя стационарное уравнение Навье–Стокса вместе с уравнением несжимаемости для определения поля скоростей жидкости и стационарное уравнение теплового баланса для определения ее температуры. На границе Г = dQ пространственной области задаются соответствующие граничные условия для скорости и температуры. При этом некоторые граничные условия задаются только на части границы (условия с недостатком), а на других участках границы задаются дополнительные условия (условия с избытком). Соответствующую краевую задачу для определения поля скоростей и температуры в области Q назовем обратной граничной задачей (или просто обратной задачей).

Рассматриваемая обратная задача является некорректной в том, что и не обладает свойством устойчивости [1, 2], малое возмущение исходных данных на участке границы с переопределением приводит к неконтролируемым ошибкам в реконструкции искомых величин. Для численного решения неустойчивых задач требуется разработка специальных методов и алгоритмов. В данной работе будет представлен конструктивный метод устойчивого численного решения рассматриваемой обратной задачи. Этот метод основан на сведении исходной некорректной задачи к вариационной задаче на минимум целевого функционала среднеквадратичной невязки [1–3]. Для решения экстремальной задачи выбрана одна из реализаций метода сопряженных градиентов. При таком алгоритме решения исходная задача заменяется на последовательное решение аналитически полученных краевых задач граничного управления, для которых соответствующие граничные данные определены полностью.

Обратные задачи восстановления тепловых режимов в геофизических процессах составляют новое направление в моделировании различных технологических и природных процессов (см., например, [4–9]). Необходимо отметить большой интерес к решению подобных задач среди специалистов в области моделирования геодинамических процессов, процессов химического синтеза и многих других отраслей знаний [7–9]. Этому способствует совершенствование методов обработки данных и накопление статистической информации о природном процессе или явлении. Решение обратных задач на сегодняшний день довольно наукоемко и сопряжено с большими затратами ресурсов ЭВМ. Благодаря сочетанию аналитических методов теории управления с алгоритмами численного решения систем дифференциальных уравнений с частными производными, в данной работе удалось получать результаты хорошего качества при сравнительно небольших затратах на компьютерную реализацию. Результаты данного численного моделирования могут дополнить уже известные методы исследования природных процессов распространения потоков вулканической лавы. Некоторые вопросы разрешимости задач граничного управления, необходимые и достаточные условия оптимальности и процедуры их численного решения исследованы в [7, 8].

Проведены серии вычислительных экспериментов, показавших работоспособность и эффективность предложенного метода. Работа продолжает исследования [9, 11].

Постановка задачи

В области Q с R ² с границей Г = dQ рассматривается установившееся конвективное движение вязкой несжимаемой неоднородной теплопроводной жидкости, находящейся в поле силы тяжести. Математическая модель представлена следующими обезразмерными уравнениями в приближении Буссинеска [4]:

• - Re (u , V) u + V- ( p ( V u + V u T ) ) = V p - RaT e ₂, (1)

V- u = 0 , (2)

• V- ( k V T ) = (u , V T ), (3) где x eQ - точка пространства; u = ( u 1 ( x ); u ₂ ( x )) - вектор скорости; T = T ( x ) - температура; p = p ( x ) - давление; p = p ( T ) - вязкость; к (T ) = k ( T )/( c p * ) - коэффициент температуропроводности; p * - температурно независимая плотность; k = k(T ) - коэффициент теплопроводности; c – удельная теплоемкость; Ra – число Рэлея [3, с. 7]; Re – число Рейнольдса [4, с. 87]; e ₂ = (0,1) - единичный вектор; ^T - транспонирование тензора; (•,•) - скалярное произведение векторов; V - градиент; V » - дивергенция.

Короткий А.И., Цепелев И.А.

На границе Г = Г 1 иГ 2 иГ 3 иГ 4 (см. рис. 1) рассматриваются следующие граничные условия:

(Vp , п) = 0,

(V p , п) = 0, Р = ⁰, а п - ( а п , п^п = 0, (V p , п^ = 0,

Г 1 :          Т = Т„

Г 2 :        (V Т , п) = 0,            u = 0,

Г ₃:        V T , п) = 0,        (V u , п^ = 0,

Г4: Т = Т4, - k (Vт,п) = ф,   (u,п) = 0, где а

= ^(Vu + Vuт) - тензор вязких напряжений. На границе Г1 жидкость втекает c априори известной температурой T1 , и ее скорость на этой границе считается неизвестной. На границе Г3 она вытекает, напряжения равны нулю, и теплообмен осуществляется только с потоком жидкости. На границе Г4 проводятся измерения температуры т4 и потока тепла ф, для скорости заданы условия непротекания и идеального скольжения. На нижней границе Г2 области заданы условия теплоизолированно-сти для температуры и прилипания для

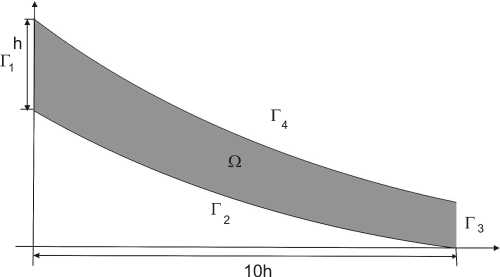
Рис. 1. Расчетная область Ω

скорости.

Наша конкретная обратная граничная задача состоит в том, чтобы по результатам измерений на Г4 температуры и теплового потока

найти температуру и поле скоростей жидкости во всей области Q, т. е. требуется найти решение задачи (1) - (4).

Задача (1)-(4) обладает свойством неустойчивости [11]. Если эту задачу решать численно, то малые ошибки в измерениях исходных данных задачи, в частности, ошибки при измерении наблюдаемых величин температуры Т4 и теплового потока ф = -k(T)дТ/ дп на Г4 и промежуточ- ные вычислительные погрешности приводят к неконтролируемым вычислительным ошибкам при определении температуры и других искомых величин в исходной задаче. Поэтому для этой задачи разрабатываются специальные устойчивые численные методы.

Обратной задаче (1) - (4) поставим в соответствие вспомогательную задачу граничного управления, которую будем называть прямой задачей. Эта задача в расчетной области описывается системой уравнений (1) - (3) со следующими граничными условиями:

Г , :     Т = Т„         u = § ,

( V p , п) = 0, (V p , п) = 0, p = 0,

Г ₂: (V Т , п) = 0,       u = 0,

Г 3 : (V Т , п) = 0, (V u , п) = 0,

Г ₄:      Т = Т ₄,       (u ,п^ = 0, а п - ( а п , п^п = 0, (V p , п) = 0.

С содержательной стороны данная прямая задача состоит в определении температуры и скорости вязкой жидкости в заданной области определения. Известны все соответствующие граничные данные в модели (5). Также искомыми характеристиками в этой задаче являются давление, вязкость и коэффициент температуропроводности. Вопросы математической корректности данной прямой задачи исследованы в работах [4, 11].

Метод решения обратной задачи

Для построения алгоритма решения задачи перейдём к вариационной постановке обратной задачи [6-9]. Пусть наблюдаемый поток тепла ф на Г4 в обратной задаче соответствует некоторому заранее неизвестному распределению скорости (управляющему параметру) u = § на грани це Г1 в прямой задаче (1)-(3), (5). Обозначим u* - компоненту скорости решения прямой задачи (Т*, u*, P*) в области Q при заданном условии на границе Г1 в (5) таком, что ф = -к(Т*)д Т*/ д п на Г4 . Пусть V - некоторое множество допустимых распределений скоростей на Г1, включающий в себя элемент * . Рассмотрим функционал качества

J ( j ) = J ( k(T j ) (v T j , n) - р ) d Г,      j e V,

Г 4

где Ге - компонента решения прямой задачи с условием u = ^ на Г1 в (5). Для искомого решения задачи данный функционал должен принимать нулевое значение при ^ = 5 , J(j ) = 0. Искомое граничное управление * на Г1 является минимизирующим элементом в вариационной задаче

J ( j ) ^ min : j e V •

Таким образом, от решения обратной задачи можно перейти к решению вариационной задачи (6). Для решения данной задачи применим устойчивый итерационный метод сопряженных градиентов Полака-Рибьера [10]. Метод сопряженных градиентов является одним из наиболее эффективных градиентных методов, если рассматривать такие критерии, как точность результатов, затраты компьютерных ресурсов и реализацию его на современных ЭВМ.

Последовательность аппроксимаций задачи (6) строится по правилу:

е(n+1) = е(n) + Yn)d(n), n =1,2,3,...,(7)

d ( n ) = j

-v j ( j ⁿ ) ), n = 1,

-vJ (j( n)) + в-n) d(n-1), n = 2,3,..., вn)=(vj(jn)),vj(jn))-vj(jn-1))) ||vj(jn-1))|I-2, n=2,3,...,

Г!

Yn) = -(d(n), vJ(е(n))) |vA(j(n))d(n)|Г2 d(n),(8)

Fj vJ(j) = qn - M(Tj(vw + vwT )| Г1 , vA^Z =(v^,n)^4 , где (w,q) - компонента решения (w,z,q) сопряженной задачи

- Re (vuYT w-vwuY ) + v-( ^CT) (vw + vwT )) = v q + zvT, v-w = 0, v - (k(T)vz) + (u^, vz)+Ra (w,e2) = ^(T^[vw + vwT, vu f + vuj ] + K^)( 7Tf, vz);      (9)

с граничными условиями:

Г 1 u Г ₂ :             z = 0,                   w = 0, (v q , n) = 0,

Г ₃:                  z = 0,             (v w , n) = 0, q = 0, k ( T j ) = 0,

Г4:      z = 2(k(Tj)(vTj,n -^),       w = 0, (vq,n = 0, и to - компонента решения (v, to, p) следующей задачи:

- Re (( v , v^ u j + (u j , v^ v ) + v •( Ц t r ) +v - ( ц '( T j ) to ( v u j + v u j ) ) = v p - Ra to e ₂, v - v = 0,

(v , v T j + (u _j , v to = v - ( k_j v to ) + v - ( k '( T _j ) to v T _j ) ;

с граничными условиями: Г 1 :       to = 0,

Г ₂ : (v to , n) = 0, Г ₃ : (v to ,n) = 0, Г ₄:       to = 0,

v = X, v = 0,

(v v , n) = 0,

(v,n) = 0,    r n - (ст n , n^n

(v p , n) = 0,

(v p , n) = 0, p = 0,

0, (v p , n) = 0, r = v v + v v ^T .

Короткий А.И., Восстановление параметров течения вязкой теплопроводной Цепелев И.А. жидкости по некоторым измерениям на ее поверхности

Вывод сопряженной задачи основан на линеаризации функций k ( T ξ + χ ) = k ( T ξ ) + k ′ ( T ξ ) T + ο ( II χ ) и µ ( T _{ξ + χ} ) = µ ( T _ξ ) + µ '( T _ξ ) T + ο ( II ^χ I ) , где T _{ξ + χ} , T _ξ компоненты решений ( T _{ξ + χ} , u _{ξ + χ} , p _{ξ + χ} ) и ( T _ξ , u _ξ , p _ξ ) прямой задачи (1)–(3), (5) для граничных условий u = ξ + χ и u = ξ на границе Γ ₁ соответственно (см. также [8]). Для вычисления шага спуска в (8), нелинейный оператор A _ξ : ξ ∈ L ²₂( Γ ₁) → k ( T _ξ ) ∇ T ξ , n ∈ L ₂ ( Γ ₄ ) для u = ξ + χ на Γ ₁ аппроксимируется выражением A _{ξ + χ} ( ξ + χ ) ≈ A _ξ ( ξ ) + ∇ A _ξ ( ξ ) χ .

Таким образом, решение исходной неустойчивой задачи (1) - (4) заменяется на устойчивый итерационный метод сопряженных градиентов решения задачи (7). Прямая задача (1) - (3), (5) и сопряжённая к ней задача (9), (10) позволяют аналитически выписать и достаточно просто вычислить градиент функционала для метода сопряженных градиентов, а задача (11), (12) позволяет вычислить шаг спуска в методе. Основная вычислительная нагрузка в реализации метода лежит на достаточно качественном и быстром решении задач граничного управления. Вопросы разрешимости таких задач (математическая корректность) исследованы в работе [11]. При достаточно большом числе Рэлея (например, большем 10⁶) итерационный метод решения прямой задачи (совместного определения поля скоростей, давления и температуры) в (1) - (3), (5) или аналогично в (9), (10) и (11), (12) замедляет сходимость и на некоторых исходных данных (например, при скачке вязкости от 1 до 10⁶) демонстрирует расходимость. Этот факт накладывает на метод соответствующие ограничения в его применимости.

Численное моделирование

Для тестирования приведенного алгоритма были разработаны программные коды в пакете OpenFOAM ( Open Source Field Operation And Manipulation ). Данный пакет – это объектноориентированная платформа, в которой на языке программирования С++ реализован широкий набор эффективных процедур аппроксимации дифференциальных операторов с различными типами граничных условий, полученных в моделях механики жидкости и газа, а также алгоритмов решения систем линейных алгебраических уравнений (СЛАУ), которые возникают после дискретизации краевых задач в пространственных областях с различной геометрией. В программные коды легко вносить изменения при изменении исходной математической модели и замене структуры вычислительного кластера. Информация о возможностях пакета представлена на официальном сайте разработчика [12].

Задачи граничного управления дискретизировались методом конечных объемов. Демонстрируемый пример рассчитывался на сетке из 10⁴ полиэдральных ячеек. Для определения поля скоростей и давления при заданном распределении температуры применялся SIMPLE-алгоритм ( Semi-Implicit Method for Pressure-Linked Equations ) [13]. Тестовые расчеты показывают, что полиэдральная сетка имеет преимущества в качестве перед гексаэдральной (что оказывает существенное влияние на скорость сходимости SIMPLE метода) и преимущества в размерности дискретных задач перед тетраэдральной сеткой (что значительно сокращает время расчетов). Для реализации данного алгоритма решались СЛАУ с положительно определенными и симметричными матрицами с реализацией многосеточного метода GAMG (Geometric Agglomerated Algebraic Multigrid) [14]. После дискретизации уравнения теплового баланса для решения СЛАУ применялся бинаправленный метод сопряженных градиентов [15]. Линейная схема Гаусса с коррекцией потока выбиралась везде для аппроксимации операторов Лапласа для аппроксимации конвективного оператора, который является доминирующим – TVD схема с ограничителем min-mod [16], что обеспечивает монотонность вычисляемых аппроксимаций температуры. Для расчетов использовалось одно ядро CPU Intel Core i5, 2,6 GHz, RAM 16 MB, OS Linux. Тестовый пример рассчитывается примерно 5 мин.

Для проведения вычислительного теста фиксируем следующие характерные значения параметров в модели, соответствующие усредненным значениям в потоке вулканической лавы [8, 9, 17, 18]: α = 10^–5 K^–1, g = 9,8 м/с², h = 10 м, ρ _ref = 2950 кг/м³, µ _ref = 3,5·10⁶ Па с, T_ref = 300 K, T _* = 1473 K, ∆ T = 100 K, κ _ref =10^–6 м²/c, c_ref = 1200 J/кг K, u_ref = 10^–3 м/c, вычисляем значения Ra ≈ 27000, Rе ≈ 2,75·10^–9.

Зависимость вязкости от температуры учитывает кристаллизацию жидкости при понижении температуры

µ(T)=min(106,exp(n(T*-T))ηɶ(φ(T)/φ*)), где exp(n(T* - T)) учитывает зависимость вязкости жидкости от температуры, и ηɶ(φ(T) /φ*) учи- тывает ее кристаллизацию (аналитическая зависимость рассматривалась в [17]).

Зависимость коэффициента теплопроводности от температуры выражается формулой [18]

k ( T ) =

'1,15 + 5,9 ■ 10 - 7 ( T - T ) 2 ,

^ 1,15 + 9,7 ■ 10 ^{- 6} ( T - T ) ² ,

T < T ,

T > T .

Зависимость вязкости и коэффициента теплопроводности от температуры показана на рис. 2.

Для проверки качества вычисления градиента функционала в задаче проводился следующий тест [19]. Для некоторого значения управления ξ на Γ ₁ ( ξ ≠ ξ ^* ) вычислим вектор e V J( § )/ 1| V J ( £ )||, где ее | 10 ^{- 9} , 0 J и рассмотрим функцию

J ( ξ + ε ∇ J ( ξ )/ ∇ J ( ξ )) - J ( ξ ) ν ( ε ) =           _{ε ∇} J ( _ξ )            = 1 + O ( ε ) .

На рис. 3 функция ν(ε) принимает значения близкие к единице в диапазоне параметра ее | 10-7,10-1 |, что демонстрирует качественное вычисление градиента функционала невязки через решение прямой и сопряженной задач.

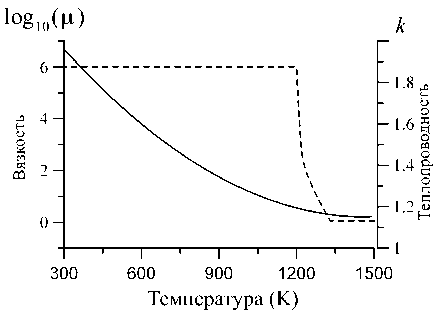
Рис. 2. Зависимости вязкости (пунктирная ли ния) и коэффициента теплопроводности (сплошная линия) от температуры

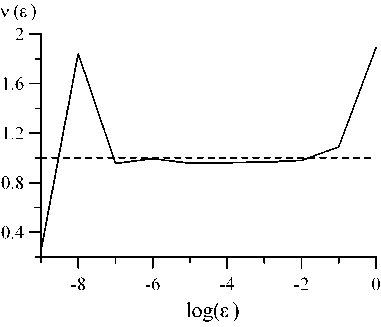
Рис. 3. Тест качества вычисления градиента функционала

Ранее в работе [9] рассматривалась аналогичная задача восстановления теплового поля в модели (1) - (4). Данная методика применялась в задаче восстановления характеристик лавового потока без учета кристаллизации вещества. В качестве управляющего параметра была выбрана температура жидкости на нижней границе области. Было установлено, что в случае доминирования диффузии в модели метод решения из [9] позволяет получить качественное восстановление искомых характеристик. Однако при увеличении магнитуды скорости наведенной конвекции точность вычисления градиента функционала падает (что проявляется в том, что не удается стабилизировать функцию ν ( ε ) близко к единице), и в методе сопряженных градиентов не удается гарантировать устойчивую сходимость аппроксимаций и получить качественное решение задачи. Подход, предлагаемый в данной работе, является альтернативным, позволяет проводить расчеты в широком диапазоне величины скорости течений жидкости и дополняет ранее изложенные результаты.

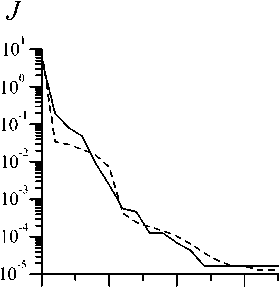
При решении обратной задачи методами сопряженных градиентов было замечено, что невязка на первых итерациях убывает довольно быстро, но затем, когда устойчивые аппроксимации

Короткий А.И., Восстановление параметров течения вязкой теплопроводной Цепелев И.А. жидкости по некоторым измерениям на ее поверхности довольно близко подходят к искомому решению, изменения невязки резко падает. Поведение итерационного процесса, демонстрируемого на рис. 4, является типичным для такого рода задач. Учитывая тот факт, что (8) является решением нелинейной экстремальной задачи y^ n ) = argmin { J ( k ( n ^{+ 1)} ): y ⁽ n) >  о } , для контроля качества итерационного процесса мы рассматривали неравенство J ( k ⁽ i ) ) >  J ( k ⁽ i ^{+ 1)}) и останавливали процесс при выполнении равенства J ( k ⁽ i ^{+ 1)})/ J ( k ⁽ i ) ) = £ 0 , где £ 0 выбирается близким к 1, например, 0,99. При этом приемлемое решение задачи достигалось за 20 итераций. В тестовом расчете принималось k *( x ) = 1000 e 1 , k ⁽⁰⁾( x ) = 100 e 1 , x еГ 1 . На рис. 5 изображены погрешности восстановления температуры ^j t = I T ^{( N} ) - ^T 1 L о , ^/ i T L,^ и ••■ ^j u = i u ⁽ ’ ) - # * L 2 ( _O , ^/ k * L2 ( r , ) ^{в расчетн}°^й-^ и

Заключение

В работе был предложен подход к численному решению некорректной обратной граничной задачи конвективного течения вязкой несжимаемой жидкости, устойчивый к погрешностям вычислений. Алгоритм решения основан на сочетании аналитических методов исследования задач граничного управления и эффективных устойчивых методов решения экстремальных задач. Построен численный метод совместного решения стационарного уравнения Навье–Стокса, уравнения несжимаемости и уравнения теплового баланса с нелинейными коэффициентами, и различными типами граничных условий на неструктурированных сетках. Реализация алгоритма в пакете OpenFOAM позволила создать программные коды для решения рассматриваемой задачи, соответствующие современному уровню развития вычислительной техники, в том числе на параллельных вычислительных кластерах. Проведены численные расчеты характерного примера обратной задачи.

Работа выполнена при поддержке Комплексной программы фундаментальных научных ис

-1-8).

1П1

p0.08

-0.06

-0.04

-0.02

Г^1” I 0

следований УрО РАН (проект 18-

0       5      10      15      20     25

Номер итерации

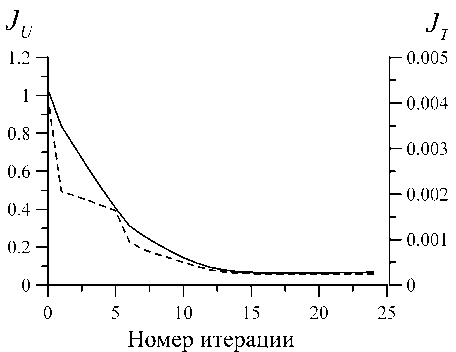
Рис. 5. Качество восстановления температуры J T (пунктирная линия) и скорости J U (сплошная линия)

Рис. 4. Функционал качества (сплошная линия) и его градиент (пунктирная линия)