Возбуждение квантового осциллятора Морзе лазерными импульсами: модельный расчет вероятности процесса

1.    Возбуждение квантового осциллятора Морзе однополярным субцикловым импульсом

Вероятность возбуждения квантового осциллятора Морзе из основного состояния однополярным субцикловым импульсом, полученная в рамках приближения внезапных возмущений [1], равна (Г(д) — гамма-функция):

w(м) _ 2вп |Г(2^с - п - iy)|2     Г(1 + iy)

⁰ ^ ^п = п! r(2so)r(2so - п + 1) Г(1 - п + iy)

где

У _ «^ ,s„ _^А^0 - п - 1/2,(2)

аа

(с) Астапенко В. А., Сахпо С. В., 2024

• (с) Федеральное государственное автономное образовательное учреждение высшего образования «Московский физико-технический институт (пациопальпый исследовательский университет)», 2024

Q — заряд осциллятора, ц — его масса, Uq — энергия диссоциации осциллятора, в — угол между осью осциллятора и электрическим полем импульса, a — параметр потенциала Морзе и

SE = I Е(t)dt(3)

- электрическая площадь импульса,

Se = V^Evt(4)

- электрическая площадь импульса униполярного гауссовского импульса, напряженность которого определяется выражением

Е(t) = Eq exp(-t2/2т2),(5)

т - длительность импульса. E q - его амплитуда..

В дальнейшем рассматривается также возбуждение осциллятора гауссовским импульсом с несущей частотой ш_с:

E(t) = Eq exp(-t2/2T 2)cos(wct).(6)

Цель работы - обобщить рассмотрение статьи [1] на импульсы произвольной длительности и несущей частоты.

• 2.    Сравнение между возбуждением осциллятора Морзе и гармонического осциллятора

Для вероятности возбуждения гармонического квантового осциллятора из основного состояния имеем

ИЯ) = ^у exp(-^).                              (7)

п!

Это выражение следует из общей формулы Швингера для возбуждения квантового осциллятора классическим электрическим током [2]. Ключевой безразмерный параметр п в случае возбуждения электрическим полем равен [3]:

п = Q- |ЕН,т)|² ,                             (8)

2цшо

E ( u q ,t ) - фурье-образ напряженности электрического поля, рассчитанный на собственной частоте гармонического осциллятора.

Сравнение вероятности возбуждения осциллятора Морзе и гармонического осциллятора в зависимости от длительности импульса представлено на рис. 1. На этом рисунке показано возбуждение гармонического осциллятора гауссовыми импульсами без несущей частоты и с несущей частотой и возбуждение осциллятора однополярным импульсом (5) из основного состояния осциллятора. Расчеты выполнены для E q = 0.1 а.е., в = 0 и для следующих молекулярных параметров: в = 2.1 а.е., U q = 0.11 а.е., ц = 18380 а.е., Q = 1 а.е. [1].

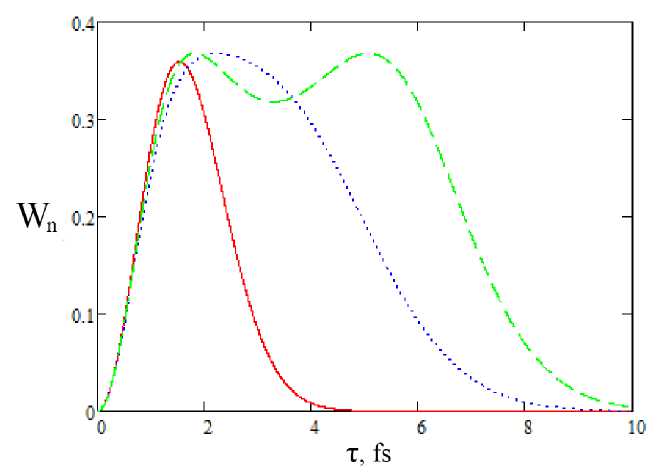
Рис. 1. Вероятность возбуждения квантового осциллятора на переходе 0 ^1 как функция длительности импульса: сплошная линия - расчет по формулам (1) - (2), пунктирная линия - расчет по формуле Швингера (7) для гауссовского импульса с несущей частотой, равной собственной частоте осциллятора, штриховая линия - расчет по формуле Швингера для гауссовского импульса с пулевой несущей частотой

Из этого рисунка видно, что приведенные выше зависимости для возбуждения осциллятора Морзе и гармонического осциллятора совпадают друг с другом только при малых длительностях импульсов, когда справедливо приближение внезапных возмущений.

3.    Модель

Наша модель основана на следующем соответствии между электрической площадью импульса и его фурье-образом:

S e ^ ¹^ ^(шом )|,

(Ю)

здесь введена собственная частота осциллятора Морзе согласно равенству

2Uo шом = А --- а. V

Это определение следует из гармонического предела потенциала Морзе. Для вышеприведенных параметров осциллятора Морзе имеем: шом = 0.198 эВ.

В дальнейшем мы используем выражения (9) и (10), подставленные в формулы (1) -(2), для расчета вероятности возбуждения осциллятора Морзе из его основного состояния. Используя предложенную модель, можно описать возбуждение осциллятора Морзе вне рамок приближения внезапных возмущений, т.е. для любых длительностей импульса и для возбуждения общим типом импульса (6) с несущей частотой.

4.    Результаты и обсуждение

Результаты расчетов т-зависимости (зависимости от длительности импульса) вероятности возбуждения осциллятора Морзе и гармонического осциллятора в различные возбужденные состояния представлены на рис. 2-3.

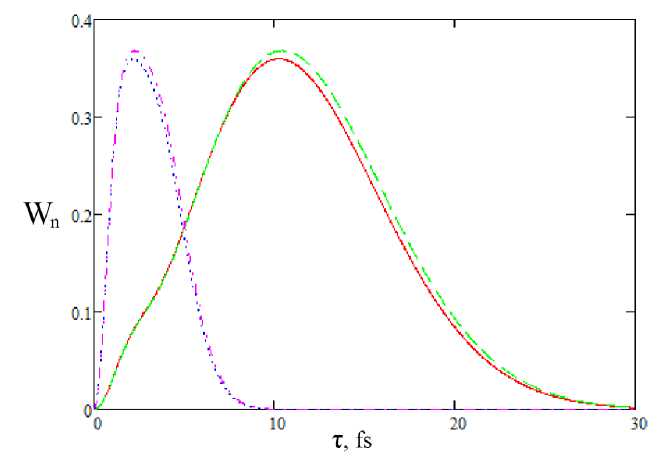
Рис. 2. Возбуждение перехода 0 ч 1: сплошная линия - осциллятор Морзе, E q = 0.03 а.е., пунктирная линия - осциллятор Морзе, Ео = 0.1 а.е., штриховая линия - гармонический осциллятор, Ео = 0.03 а.е.. штрих-пунктирная линия - гармонический осциллятор. Ео = 0.1 а. е.. w_c = w q

Из рисунка 2 видно, что при возбуждении перехода 0 ^1 практически нет разницы между осциллятором Морзе и гармоническим осциллятором при малых и больших значениях амплитуды импульса. Это связано с тем, что при малой энергии возбуждения осциллятор Морзе эквивалентен гармоническому, а при высоком уровне возбуждения между этими осцилляторами наблюдается существенная разница, как это видно из рис. 3.

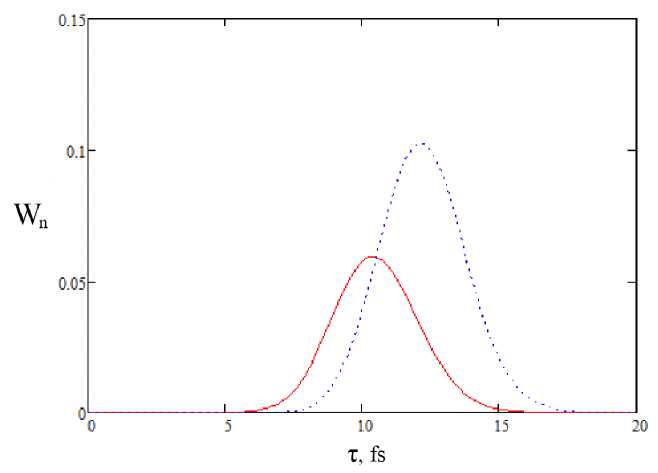
Рис. 3. Возбуждение перехода 0 ^ 15: сплошная линия - осциллятор Морзе, пунктирная линия -гармонический осциллятор, E q = 0.1 а.е., w _c = w q

Заметим, что максимум вероятности возбуждения для гармонического осциллятора смещается в сторону более длинных импульсов по сравнению с осциллятором Морзе для возбуждения на высокий энергетический уровень.

Спектры вероятности возбуждения, т.е. зависимость вероятности от несущей частоты импульса, показаны на рис. 4-6 для возбужденных состояний с низкой и высокой энергией.

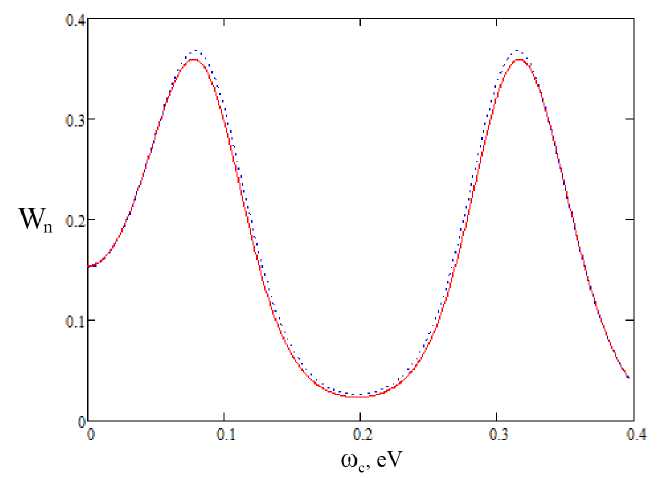
Рис. 4. Возбуждение перехода О Д 1 . т = 7.2 фс, Е о = 0.1 а.е.: сплошная линия - осциллятор Морзе, пунктирная линия - гармонический осциллятор

Из рисунка 4 видно, что при возбуждении на низкоэнергетический уровенв разницы между осциллятором Морзе и гармоническим осциллятором практически нет, тогда как при возбуждении на высокий уровенв эта разница существенна (рис. 5, 6).

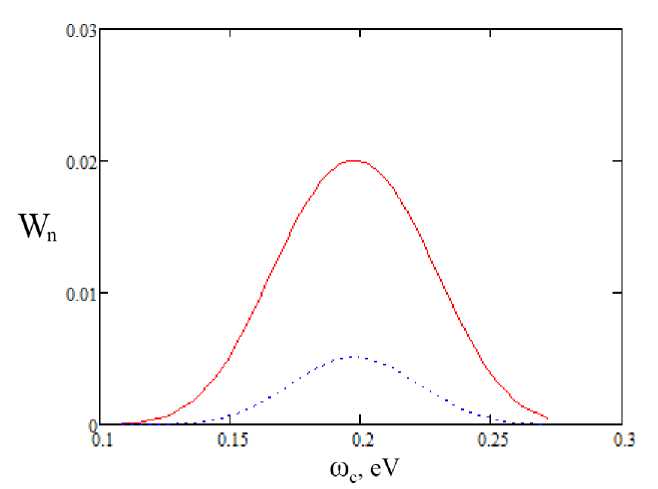
Рис. 5. Возбуждение перехода 1 Д 12, т = 7.2 фс, Ео = 0.1 а.е.: сплошная линия - осциллятор Морзе, пунктирная линия - гармонический осциллятор

Рисунки 5 и б демонстрируют также переход от слабого возмущения к режиму сильного возмущения при возбуждении осциллятора лазерным импульсом. В последнем случае вместо максимума в спектре вероятности возбуждения возникает минимум, и появляются два боковых максимума.

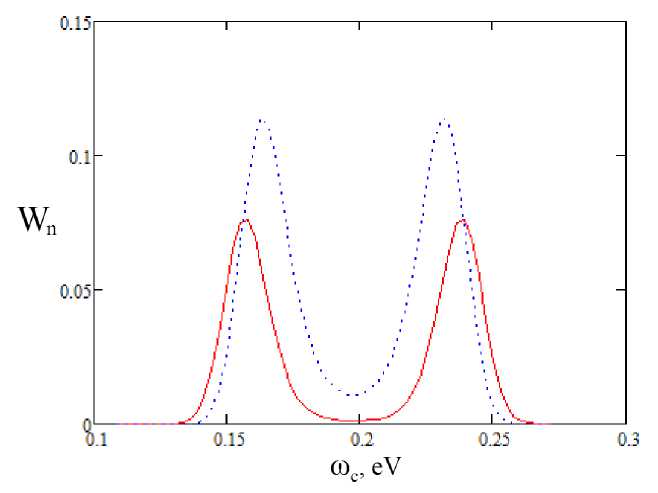
Рис. 6. Возбуждение перехода 0 ^ 12, т = 14.4 фс, Е о = 0.1 а.е.: сплошная линия - осциллятор Морзе, пунктирная линия - гармонический осциллятор

Исследование выполнено за счет гранта Российского научного фонда № 24-49-10004, / project / 24-49-10004/