Воздействие режимов лазерного оплавления на адгезионную прочность клеевых покрытий системы железо-хром-бор-кремний

Широко известен способ получения износостойких покрытий сочетанием плазменного напыления с последующим лазерным оплавлением [ 3 ] . Этот метод весьма успешно зарекомендовал себя при изготовлении и восстановлении длинномерных, крупногабаритных деталей и деталей сложной конфигурации. Однако данная технология достаточно затратная.

Покрытия после лазерного оплавления обладают высоким комплексом физикомеханических и эксплуатационных свойств. Для сравнения часть образцов подвергали лазерному оплавлению после клеевого метода нанесения покрытий.

Покрытия, нанесённые на деталь, в процессе эксплуатации подвергаются воздействию механических нагрузок, а адге- зионная прочность лимитирует их применение. Лазерная обработка клеевых покрытий позволяет повысить прочность сцепления покрытия с основой при максимальном сохранении исходной структуры и свойств порошка. Для оценки работоспособности изделия подвергаются испытаниям на отрыв по ГОСТ 14760-69 «Метод определения прочности при отрыве».

Целью работы являлось исследование адгезионной прочности и фазового состава покрытий из самофлюсующихся сплавов на железной основе (клеевых и после плазменного напыления, оплавленных лазером и горелкой).

Обозначения:

А – площадь торцевой поверхности штифта, мм²;

B ij – коэффициенты регрессии, описывающие направление и степень влияния каждого из факторов на параметры оптимизации;

С В – концентрация бора в обмазке;

С MD – концентрация связанных атомов покрытия и подложки;

d l – диаметр луча лазера, мм;

d – диаметр штифта мм;

D 2 – комплексы с насыщенными связями, образуемые атомами подложки;

Δ E ∂ – часть энергии диссипирования пятна за счёт скоростей, вязких деформаций и напряжений, Дж;

Н – микротвёрдость, МПа;

I – ток дуги при плазменном напылении покрытий, A;

К – константа скорости образования квазихимических связей;

k – постоянная Больцмана;

k пер – коэффициент перекрытия лазерных дорожек;

2 М – атомные комплексы, образуемые активированными атомами частиц покрытия;

2 MD – конечное состояние системы комплексов связанных атомов покрытия и подложки после преодоления потенциального барьера, при котором образуется прочная связь между частицами подложки и покрытия;

2 М + 2 D – активированное состояние системы атомных комплексов, образуемое атомами покрытия и подложки на высоте потенциального барьера;

2 М + D 2 – начальное состояние системы комплексов, образуемое разобщёнными активированными атомами частиц покрытия и подложки;

N – мощность лазерной установки ЛГН-702, Вт;

n – число факторов;

N ef – эффективная мощность, передаваемая слою покрытия и превращаемая в тепло, с поправкой на потери (т.е. мощность, непосредственно передаваемая слою покрытия);

P e – внешнее давление в области контакта луча лазера и покрытия, ГПа;

P н – давление плазмообразующих газов при напылении, ГПа;

P 0 – усилие, соответствующее моменту отрыва покрытия от штифта, ГПа;

Q – число опытов;

q _п – поток теплоты в покрытии;

ΔS a – изменение энтропии в области присоединения покрытия к основе,

Дж ;

К ⋅ моль

∆F a – площадка активации, м²;

T – температура на границе покрытия и основы, К

T k – температура в области контакта покрытия и основы, К;

t – время движения луча лазера, с;

Т – температура в центре пятна, К;

T 0 – начальная температура, 300К;

U – напряжение электрической дуги при плазменном напылении, B;

∆ U а – изменение внутренней энергии в области присоединения покрытия к основе;

• V    – обобщённая скорость движения луча лазера относительно детали, мм/мин;

• V 1    = 50, V 2 = 100, V 3 = 150, V 4 =200, V 5 = 300 – скорости движения луча лазера относительно детали, мм/мин;

ξ – координата реакции;

• Х 1 – скорость перемещения лазерного луча, мм/мин;

Х 2 – диаметр луча лазера в месте соприкосновения с поверхностью материала, мм;

Х 3 – коэффициент перекрытия лазерных дорожек;

∆х = d l – протяжённость области, примыкающей к пятну расплава, м;

Y – параметр оптимизации адгезионной прочности;

Ф – термодинамический потенциал Гиббса;

∆ Ф а – величина потенциального барьера энергии Гиббса для активной области , в которой реализуются связи между атомами основы и частицами покрытия;

∆ Ф 0 – доля приращения термодинамического потенциала Гиббса без учёта включений, Дж;

Ф> - диссипативная функция, Вт;

Ω – атомный объём;

π ( d l /2)² – площадь пятна лазерного луча;

^ _ав — компоненты тензора скоростей деформации, с 1 ; а , в = 1, 2, 3;

λ – коэффициент теплопроводности, Вт/(см∙град);

σ – коэффициент поверхностного натяжения, Дж/м²;

σ αβ – компоненты тензора напряжений, Па;

σ 0 – коэффициент поверхностного натяжения без учёта примеси бора, Дж/м²;

σ _max – максимальная прочность сцепления покрытия и основы, МПа;

σ _с – прочность сцепления покрытия и основы, МПа;

τ – время, в течение которого луч лазера проходит отрезок, равный его диаметру, с;

1/ τ_а – частота колебаний атомов в решётке кристалла.

Индексы : В - бор; ef - эффективный; ij – номер коэффициента модели (совпадает с порядковым номером); max – максимальный; ∂ – диссипация; а – активация; e – внешний; l – луч лазера; MD – прочная связь между атомами подложки и покрытия; н – напыление; нас – насыщенный; п – покрытие; пер – перекрытие; с – сцепление покрытия и основы; ш – штифт; α , β = 1, 2, 3 – индексы координатных осей в тензорах напряжений и скоростей деформации (по этим индексам выполняется суммирование).

Методика исследований. В качестве материала для нанесения клеевых покрытий и напыления использовали самофлю-сующийся сплав из порошка ПР-Х4Г2Р4С2Ф следующего химического состава (в %): Fe (83.1 – 87.6), B (3.3 – 4.3), Cr (3.5 – 4.5), Si (2.0 – 2.5), Mn (2.0 – 2.5), C (1.0 – 1.2), V (0.5 – 0.9), Al (0.05 – 0.5), Cu (0.05 – 0.5). На подготовленную поверхность штифтов клеевым способом его наносили кисточкой, а также методом плазменного напыления с использованием установки УПУ-3Д с источником питания ИПН-160/600 и плазмотроном ПП-25 на режимах: I = 250 A, U = 80 B, P = 0.06 ГПа. Толщина слоя составляла 0.6 мм.

Исследования адгезионной прочности проводились на разрывной машине «RIEHLE» с плавно изменяющимся усилием от 0 до 50000 Н на штифтах из стали 40Х, вставленных один в другой и притёртых друг к другу. Торцы конусов представляли собой концентрические кольца. Диаметр меньшего конуса –12 мм, большего – 20 мм. Такая конструкция штифтов позволяет получить более однородный отрыв.

Применявшийся метод штифтовой пробы основан на непосредственном определении силы, направленной перпендикулярно к напылённой и оплавленной поверхности и отрывающей покрытие от основного материала [ 4, 5 ] . Для закрепления образца в разрывной машине использовались специальные оправки, соединяемые с захватами разрывной машины при помощи гибких тросов. Это обеспечивало перпендикулярность усилия отрыва торцевой поверхности образца. Применялась минимальная скорость нагружения, обеспечивающая статический характер нагрузки. Усилие P о , соответствующее моменту отрыва покрытия от штифта, отмечалось на шкале, проградуированной в килограммах, а затем переводилось в ГПа. Прочность сцепления и площадь торцевой поверхности штифта определялись по формулам

" с = А '

A =

п • d ¹

С целью сопоставления получаемых значений σ с для разных образцов толщина напыляемых и клеевых покрытий выдерживалась постоянной и составляла 0.6 мм. Неизменным сохранялся интервал времени между дробеструйной обработкой и нанесением клеевых покрытий, а также напылением. Для обеспечения статистической достоверности использовалось по десять образцов с покрытиями, нанесёнными при одинаковых режимах.

Поверхность штифта под клеевые и плазменно-напылённые покрытия готовили следующим образом: вначале её обезжиривали этиловым спиртом, затем производили обдувку дробью. После дробеструйной обработки штифт проворачивали в приспособлении для устранения погрешности. На поверхность образца наносили порошковый сплав клеевым методом (в порошковый слой для клеевого покрытия добавлено 3% клея «AGO» к ацетону) или напыляли [ 1 ] . Далее на плазменно - напылённый слой наносилось поглощающее покрытие (жёлтая гуашь). При клеевом методе вместо него использовалась легирующая обмазка на основе карбида бора.

Оплавление осуществляли непрерывным лазером ЛГН-702 мощностью N = 800 Вт и диаметре пятна лазерного луча от d l = 1.0 10^–3 м до d l = 3.0 · 10^–3 м со скоростями перемещения V 1 = 50 мм/мин, V 2 = 100 мм/мин, V 3 = 150 мм/мин, V 4 = 200 мм/мин, V 5 = 300 мм/мин и коэффициентами перекрытия k пер = 0.8 и k пер = 1.2 с целью получения единого фазового состава и заданных свойств по всей толщине покрытия.

В случае лазерного легирования клеевых покрытий карбидом бора режимы оплавления подбирали, а полученные данные исследовали одним из методов математического планирования – методом полного факторного эксперимента [ 6 ] .

Поскольку число варьируемых параметров невелико, оказалось возможным реализовать полную реплику, в которой число опытов Q = 2 в степени, соответствующей числу факторов n, позволяющую в ходе эксперимента варьировать одновременно несколько параметров различной физической природы и получать раздельную, независимую оценку коэффициентов, что невозможно, например, при реализации дробной реплики. При этом необходимо, чтобы все независимые переменные, влияющие на процесс, изменялись на двух уровнях: минимальном и максимальном.

Серия состояла из 8 основных опытов. Полученная модель считалась линейной и учитывала взаимодействие факторов

• Y=B 0 +B 1 X 1 +B 2 X 2 +B 3 X 3 +B 12 X 1 X 2 +B 13 X 1 X 3 +B 23 X 2 X 3 . (2)

Для составления таблицы данных (матрицы планирования) находили пределы изменения основных входных параметров, в качестве которых были приняты технологические параметры лазерной обработки (табл. 1, 2).

Таблица 1. Матрица планирования эксперимента

Природа варьируемого фактора	V , мм/мин	d l , мм	k пер
Код фактора	Х 1	Х 2	Х 3
Основной уровень	100	2	1
Интервал варьирования	50	1	0.2
Величина факторов в опытах (по номерам) основной матрицы
Опыт  1	—	—	—
2	+	—	—
3	—	+	—
4	+	+	—
5	—	—	+
6	+	—	+
7	—	+	+
8	+	+	+

Таблица 2. Зависимость σ с от режимов обработки

№ образца	Вид, режимы обработки и код			σ с МПа
	Х 1	Х 2	Х 3
	Клеевое покрытие, оплавленное лазером
1	50	1	0.8	92
2	150	1	0.8	67
3	50	3	0.8	73
4	150	3	0.8	53
5	50	1	1.2	76
6	150	1	1.2	58
7	50	3	1.2	70
8	150	3	1.2	42
	Плазменное покрытие без оплавления
9	–	–	–	31
	Плазменное покрытие, оплавленное лазером
10	50	1	0.8	156
11	100	1	0.8	129
12	300	1	0.8	113
	Плазменное покрытие, оплавленное горелкой
13	–            |	–            |	–	142

Технологические факторы Х 1 , Х 2 и Х 3 выбирали исходя из возможности их изменения при условии точного измерения их величин, а также учитывая их взаимную независимость (ортогональность).

Для оценки достоверности результатов и адекватности модели повторные опыты проводили трижды на основном уровне с использованием карбида бора в качестве упрочняющей добавки.

Параметром оптимизации служила прочность сцепления покрытия и основы Y .

Рентгеновские съёмки производились на дифрактометре ДРОН 3.0 при скорости поворота образца 1 град/мин в медном мо-нохроматизированном излучении в максимально возможном интервале углов от 10° до 75° для качественного и количественного фазового анализа.

Результаты исследований и их обсуждение. Фактором, лимитирующим прочность сцепления газотермических покрытий из самофлюсующихся сплавов на основе железа, является раскисление окисных плёнок между покрытием и подложкой и установление химических связей. Время, необходимое для раскисления ок- сидов железа при Т = 1300 – 1500 К, составляет 0.75 - 0.9 с [7].

В процессе исследования наблюдался адгезионный и адгезионно-когезионный характер разрывов образцов, когда покрытие отрывалось полностью либо часть его оставалась на штифте, причём первый случай характерен для больших скоростей сканирования луча лазера.

Разрушение покрытия начинается с торцов [ 8 ] , где меньше толщина клеевого слоя и существуют дефекты, т. е. нет удовлетворительного контакта клея с материалом. В этих местах концентрируются значительные напряжения. При увеличении нагрузки в них возникают микротрещины, которые постепенно распространяются к центру склеивания. Когда число микротрещин достигает определённого уровня, создаются условия для их соединения в трещину значительных размеров, что приводит к разрушению.

Для покрытий, напылённых плазмой без легирования, максимальное значение σс = 156 МПа наблюдается при минимальной скорости движения луча лазера V1 = 50 мм/мин (см. табл. 2, образец № 10), с повышением скорости луча относительно детали до V5 = 300 мм/мин σс = 113 МПа (образец № 12). Это связано с сокращением времени нахождения детали в зоне лазерного нагрева.

Минимальное значение σ с = 31 МПа наблюдается у покрытий, напылённых плазмой без оплавления, из-за наличия пор и большого количества окисных плёнок (образец № 9).

Что касается клеевых покрытий, легированных В 4 С, то наибольшая прочность сцепления покрытия с основой σ с наблюдается при V 1 = 50 мм/мин, d l = 1 мм и k пер = 0.8, а именно 92 МПа (образец № 1). Покрытие находится в зоне воздействия луча лазера достаточно долго и успевает полностью проплавиться. С увеличением коэффициента перекрытия до 1.2 прочность сцепления снижается до 76 МПа (образец № 5). Это связано, по-видимому, с расфокусировкой луча.

При V 1 = 50 мм/мин, d l = 3 мм и k пер = 0.8 σ с уменьшается до 73 МПа (образец № 3). Это связано, по-видимому, с уменьшением энерговклада. При той же скорости и том же диаметре луча лазера, но при увеличении коэффициента перекрытия до 1.2 (образец № 7) σ с уменьшается до 70 МПа. С повышением скорости луча лазера относительно детали до 150 мм/мин при d l = 1 мм и k пер = 0.8 (образец № 2) σ с снижается до 67 МПа. Это связано с тем, что время нахождения покрытия в зоне лазерного воздействия уменьшилось. При той же скорости и том же диаметре луча, но с увеличением коэффициента перекрытия до 1.2 (образец № 6), σ с снижается до 58 МПа. При V 3 = 150 мм/мин, d l = 3 мм и k пер = 0.8 (образец № 4) σ с уменьшается до 53 МПа. При максимальных значениях скорости, диаметра и коэффициента перекрытия V 3 =

150 мм/мин, d l = 3 мм и k пер = 1.2 (образец № 8) σ с минимальна – 42 МПа.

Полученная адекватная модель поверхности отклика позволяет судить о степени влияния параметров Х 1 – Х 3 на адгезионную прочность Y при лазерном легировании клеевых покрытий.

y = 67.458 – 9.708 X 1 – 6.042 x 2 – 5.958 x 3 – 5.375 X 1 X 2 . (3)

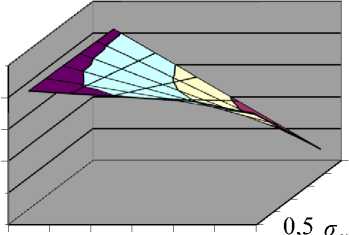
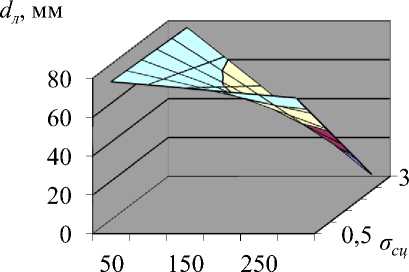
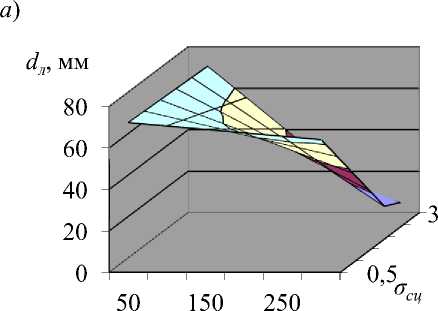
Построены зависимости прочности сцепления покрытия с основой после лазерного легирования В 4 С от коэффициента перекрытия k пер = 0.8, 1.0 и 1.2 (рис. 1). Отчётливо прослеживается зависимость адгезионной прочности для клеевых покрытий, легированных В 4 С: с повышением скорости луча лазера σ с уменьшается. При V 1 = 50 мм/мин время нахождения покрытия в зоне лазерного нагрева больше, покрытие проплавляется сильнее, что и вызывает повышение адгезионной прочности. При увеличении диаметра луча до 3 мм вследствие расфокусировки уменьшается энерговклад, покрытие проплавляется слабее и σ с меньше, чем при d l = 1 мм. При обработке покрытий с коэффициентом перекрытия 0.8 из-за наложения лазерных дорожек одной на другую происходит дополнительный переплав покрытия, приводящий к увеличению σ с . Для плазменных покрытий без оплавления σ с наименьшая из-за трещин, крупных сфероподобных полостей и мелких пор, а также большого количества окисных пленок. У плазменных покрытий, оплавленных лазерным излучением, с уменьшением скорости обработки σ с повышается. В случае испытаний плазменно-напыленных покрытий, оплавленных горелкой, σ с зависит от выбранных режимов оплавления и несколько меньше, чем при оплавлении лучом лазера.

d_л , мм

сц

20 0

50    150   250

V , мм/мин

V , мм/мин

V , мм/мин

б )

в )

Рис. 1. Зависимости прочности сцепления покрытия после лазерного легирования В 4 С: а ) k пер = 0.8, б ) k пер = 1, в ) k пер = 1.2

На свойства покрытий, как известно, оказывает влияние не только прочность сцепления, но и их фазовый состав, особенно количество упрочняющей фазы. Данные рентгеноструктурного анализа клеевых, плазменных покрытий после оп- лавления лазерным лучом и горелкой представлены в таблице 3 и 4.

Из таблиц видно, что с повышением скорости движения луча лазера, ростом диаметра луча и коэффициента перекрытия уменьшается количество боридов железа, а также адгезионная прочность σ _с .

Таблица 3. Состав фаз после нанесения клеевых покрытий и лазерного легирования

В 4 С

	Номера образцов и режимы обработки
	1	2	3	4	5	6	7	8
	V 1 = 50	V 3 =150	V 1 =50	V 3 =150	V 1 =50	V 3 = 150	V 1 =50	V 3 =150
Фазы	d l =1.0	d l =1.0	d l =3.0	d l =3.0	d l =1.0	d l =1.0	d l =3.0	d l =3.0
	k пер =	k пер =	k пер =	k пер =	k пер =	k пер =	k пер =	k пер =
	=0.8	=0.8	=0.8	=0.8	=1.2	=1.2	=1.2	=1.2
Fe	27.3	34.4	33.1	37.8	30.6	29.3	30.7	28.3
Бориды Fe	29.5	27.1	27.9	27.1	28.6	25.1	29.1	22.3
Карбид Fe	11.5	8.5	10.1	11.6	8.4	9.7	13.0	9.0
Карбиды	23.3	21.9	22.1	19.3	25.8	23.3	23.6	26.3
Бориды Cr	8.4	8.1	6.7	4.2	6.3	12.6	3.7	14.0
Н, МПа	1136	1313	1223	1210	1180	1285	1243	1386

Таблица 4. Состав фаз в зависимости от режимов обработки для оплавленных горелкой и лазером плазменных покрытий без легирования (при dl =1.0 мм, kпер= 0.8)

Фазы	Номера образцов и режимы обработки
	9	10	11	12
	Оплавленны	е лазером плазменны	е покрытия	Напылённое и оплавленное горелкой покрытие
	V 1 =50	V 2 =100	V 3 =300
Fe	56.2	55.7	55.8	27.6
Бориды Fe	13.9	14.9	14.0	16.8
Карбид Fe	7.1	7.5	7.6	10.4
Карбиды	12.7	14.5	15.6	27.0
Бориды	8.6	10.4	7.0	16.7
Н, МПа	939	1050	1121	1015

Расчёт адгезионной прочности в зависимости от концентрации бора в покрытии. Теорию прочности сцепления рассмотренных выше покрытий построим на основе следующих представлений: кинетика образования квазихимических сил изучена исходя из модели, в соответствии с которой процес- сы протекают только в области, примыкающей к пятну расплава, протяженностью ∆x = dl (см. рис. 2, 3) [8]. Положения, лежащие в основе данной модели, подробно описаны в работе [9].

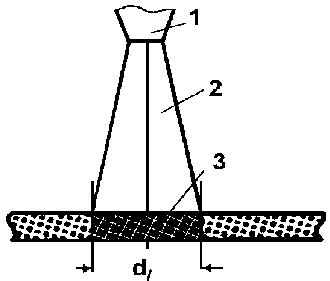
Рис. 2. Схема расположения луча лазера и оплавляемого им покрытия: 1 – лазер; 2 – луч; 3 – расплав

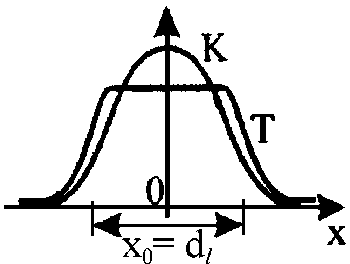
Рис. 3. Изменение константы скорости образования квазихимических связей в зависимости от координаты х луча лазера

На рис. 3 показано, что константа скорости образования квазихимических связей К заметно отлична от нуля только в области пятна, поскольку экспоненциально зависит от температуры:

К = —exp l

Та      ।

—

Аф ^ , ^Ф_a = ^U_a — TAS a + P e Q ., (4) kT k J

В (4) у нас 1 – частота атомных коле

Та баний в кристаллической решётке металла; k – постоянная Больцмана; Tk – температура в области контакта частиц покрытия с основой; АФа - изменение термодинамического потенциала Гиббса, отнесённое к

атомному объёму Q в котором, согласно модельным представлениям [8, 9], протекает процесс образования прочных квази-химических связей между парами атомов М частицы покрытия и D подложки; AU _a -соответствующее этому процессу изменение внутренней энергии; A S_a - изменение энтропии; P e – внешнее давление в области контакта.

Для оценки температуры Т в области пятна лазера можно воспользоваться величиной баланса тепловых потоков q e от лазе-

ра и q _п в покрытии.

Имеем:

qe

Nef п (di/ 2)

q n = ^Х

T — T 0 , d l / 2

q n = q e . (5)

Из (5) следует, что

2 N          0

Т = Т0 +----ef— = Т 0 + Т п • Хп • dl

Здесь Т 0 – начальная температура по- 0

крытия; Т – температура в центре пятна; N ef – эффективная мощность лазерного излучения, передаваемая металлу; Х п - ко-

эффициент теплопроводности покрытия; d l – диаметр лазерного пятна (рис. 2).

Для точной оценки температуры T k в области контакта частиц с подложкой можно воспользоваться известным соотношением [8, 9]:

T = b n T + b о T o . (7) ^ь п ⁺ b о

В ^{(7) ь} п = V ^р п ^с п ^Х п ^, b о = V ^р о C о ^Х о ^{- ко} эффициенты аккумуляции теплоты для покрытия и, соответственно, основы; р п -плотность покрытия; С п - теплоёмкость покрытия; р о - плотность материала подложки; Х о - теплоёмкость подложки.

Суть применяемой нами модели [8, 9] состоит в следующем. В частицах покрытия атомы М за счёт высокой температуры частиц (6) в области лазерного пятна находятся в активированном состоянии с ненасыщенными междуатомными связями, а атомы подложки D связаны попарно так, что на каждую пару атомов частицы 2М приходится пара D 2 связанных атомов в решётке металла подложки. Это состояние пар атомов 2M + D 2 на рис. 4 представлено точкой А. Чтобы разорвать связь в паре D 2 системе атомов 2M + D 2 требуется преодолеть потенциальный барьер АФ_а вдоль координаты реакции ^. Активированному состоянию системы 2M + 2D отвечает (рис. 4) точка В. Необходимая системе энергия активации АФ_а получается за счёт тепловой флуктуации в системе при достаточно высокой температуре контакта (7). В системе атомов 2M + 2D становится возможным формирование прочных квазихи-мических связей, и она переходит в состояние, показанное на рис. 4 точкой С. Имеем здесь состояние 2MD.

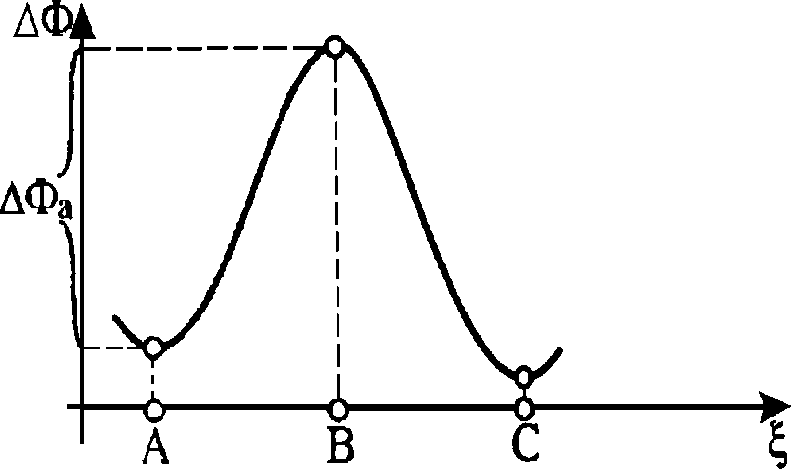
Рис. 4. Зависимость термодинамического потенциала Гиббса образования квазихимических связей от координаты реакции

Сказанное соответствует топохимической реакции [8]:

2M + D ₂ > 2M, 2D >  2MD,      (8)

Если ввести концентрацию C MD связанных пар атомов частицы покрытия и подложки, то скорость протекания её можно выразить уравнением:

d l C MD = ( 1 - C MD ) K - dt

Здесь AF_a - площадь области контакта для системы атомов 2M + 2D,   ■   8Ф _А -

’ - AE_a =---< 0

⁸     81

диссипация термодинамической энергии АФ_а за счёт вязких процессов в области пятна. Можно положить для диссипативной функции A E 8 :

АЕд= 1 аареар-         (12)

В (9) константа скорости реакции (8) представлена уравнением (4). Учитывая, что реакция (8) протекает вдоль лазерного пятна, т.е. вдоль координаты x , как это показано на рис. 3, имеем:

dC _MD dC _MD dx dC _MD , (10) dt dx dt dx

В (12) о_а р - тензор вязких напряжений (а, в = 1, 2, 3 ), Ё ^ _ар - тензор скорости вязких деформаций в металле.

Далее, как известно

8 Ф

----= ( 7 ,

8 F

где V – скорость перемещения лазерного луча.

В выражении (4) можно приближённо принять, различая АФ _а по малым значениям AF a и t = x / V :

АФ а «АФ 0 +

I аг /

{ ⁸F 7 о

. Р  ( дФ ]

■AF + --- t, a A t J о

– коэффициент поверхностного натяжения, для которого, согласно [7], можно положить

7 = 7 о - 7 1 С в , (14)

где C B – концентрация бора в области контакта.

Интегрируя (9) с учётом разложения (11), имеем:

• - Ц1 - C^)« 2K0sh fAEd dj- )• T-,

MX0 l     2V j_A e

Здесь положено:

• 1 f AФ   a A F   ст,C. A F )

K„ = —exp\a-0—a‘—B—a ,

• 0  та    (  kT.     kTt       kTtJ

Далее можно принять, что C MD << 1 и

—ln(1 — Cmd) ® Cmd,

• а также разложить в ряд ^f A E d ^d> | для

L kT 2V J малых значений аргумента:

fAEa d, )  AE, d 1 fAEa d, )3

2sh ~ 1+ ...

L kT_k 2V J   kT_k V 3 L kT_k 2V J

Представляется естественным положить [8] для прочности сцепления покрытия с основой ac / ^max  CMD,    (19)

Тогда находим окончательно:

_п ~ _n v ^f d_+ 1 , (20) ^ac ~ ^ac max ^K 0 1 у + ^..‘ I

Полученное выражение отражает зависимость прочности сцепления от величин d l , V и C B , наблюдавшуюся в эксперименте.

Выводы

• 1.    Максимальное значение адгезионной прочности σ _с наблюдается у оплавленных лазером плазменных покрытий без легирования при минимальной скорости движения луча лазера относительно детали.

• 2.    Для клеевых оплавленных лазером покрытий с повышением скорости луча лазера относительно детали от 50 мм/мин до 150 мм/мин, увеличением диаметра луча от 1 до 3 мм и ростом коэффициента перекрытия от 0.8 до 1.2 количество боридов железа уменьшается и снижается адгезионная прочность σ _с.

• 3.    Экспериментально и теоретически установлено, что увеличение концентрации бора С В приводит к повышению адгезионной прочности и улучшению структуры границ зёрен.