Возможность использования инновационных моделей при уточнении наиболее оптимального подхода по управлению поведением коммерческой организацией

Актуальность рассматриваемой проблемы обусловлена рядом существенных факторов, суть которых может быть сведена к следующему очевидному в настоящее время постулату: нецелесообразно рассматривать современную экономическую ситуацию в любой организации Для цитирования

или в целом по отрасли без использования имитационных или математических методов и моделей. При этом нужно учитывать, что нет единообразных методологий исследования систем, базирующихся на экономико-математических подходах к анализу устойчивости и управляемости социальных систем, которые могут быть

This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License

использованы в различных организациях и отраслях, так как в любой ситуации подвергается индивидуальному анализу внешняя и внутренняя среда, определяющая направленность исследований. Все это диктует потребность в разработке теоретически аргументированного и практически реализуемого аппарата анализа влияния оптимального управления на дальнейшую стратегию организаций и целых регионов.

Практическое моделирование использует не только теоретические подходы, но и управленческие вопросы, поэтому сравнивать теоретические и математические модели не совсем корректно. Неразбериха между моделями такого сорта появляется еще на раннем при изучении экономической теории. Заметим, что понятие спроса существует как самостоятельная единица, имеет самостоятельное значение, а модель спроса представима в виде возрастающей кривой и как любая модель содержит различные явные и неявные условия.

Формализованное представление задачи

Вообще говоря, любая используемая в экономических исследованиях или управленческой практике экономико-математическая модель представляет собой самостоятельный объект, который не может полностью описывать происходящие процессы. Следовательно, экономико-математическую модель это автономный объект, способный отвечать на возникающие вопросы, с другой стороны, этот объект может и сам предъявлять требования различного характера в экономической или управленческой сфере. Для этого модели должна соответствовать определенная атрибутика, в том числе и паспорт модели, являющимся идентификатором моделей и позволяющим различать модели. Рассмотрим возможные варианты структуры верхнего уровня, которая может быть использована для классификации данных, отражаемых в паспорте модели:

• 1.    Представление (указание) обозначенного объекта моделирования.

• 2.    Список сторон функционирования объекта, которые должны быть отражены моделью.

• 3.    Перечень вопросов, а также задач, реализация которых должна произойти с использованием построенной модели.

• 4.    Детализированное описание исходного объекта моделирования, включающее его представление в виде целостной системы; при этом для упрощения будем использовать хорошо сформулированные экономико-математические предпосылки.

• 5.    Формализованное представление аппарата, используемого при построении модели,

• 6.    Способы инструментального и функционального распознавания, используемые при построении модели.

• 7.    Способ представления границ допустимого истолкования элементов модели.

набора переменных, их взаимосвязей и других частей модели.

Проведение усовершенствования и оптимизации структур организации, стремящейся повысить свою рентабельность, а также построение оптимальных математических моделей и наибольшая формализация поставленных задач, позволяют в полном объеме использовать средства вычислительной техники.

Первоначально зададимся вопросом: что мы можем сказать о числе аргументов числовой функции, учитывая область значений, которые она принимает сфере единичного радиуса? В общем случае ответ будет однозначен: ничего точно сказать нельзя. Однако, представляется возможным подтвердить, что иногда получит неожиданные оценки числа аргументов.

• 1.    Первоначально сформируем форму, проанализировав квадратичную форму f ( x ) = ( Ax , x ) с нормальным оператором А и пометив, используя круглые скобки, скалярное произведение принадлежащее соответствующему пространству Cn. Очевиден факт того, что число вершин многоугольника, определяющего числовую область матрицы, выстроенной в комплексной плоскости, не может ответить на вопрос о числе собственных чисел, с учетом их кратности, поскольку мы не знаем число вершин, находящихся внутри этого многоугольника. Известно лишь о существовании взаимно однозначного соответствия между вершинами многоугольника и собственными числами.

• 2.    Отыщем плотность множества относительно центра, определенного как точка начала координатных осей. Первоначально сформулируем определение.

Определение. Величина w, в формуле (1), определяет плотность М относительно точки начала координат, определяющей центр:

где р соответствует расстоянию между точками i и О, р определяет меньший из углов определенных векторами pt и р. .

Найдем плотность числовой области соответствующего оператора в виде:

помощи (4) установим количество ограничений

на используемые варианты игры:

w (A) =

- max ^

2 A * A

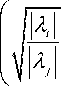
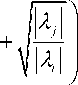
° ‘j cos —

Плотность w ( A ) представим const относительно преобразований плоскости, воспользовавшись определением диагональной доминанты:

I au\ > EI a^ ,¹=1, n .

i * j

Затем сформулируем утверждение, которое будет использовано на этапе графической реализации модели управления коммерческой организации, помогающей проведению анализа различных ее вариантов с дальнейшим выбором

наилучшего из них.

Утверждение. Реализация неравенства (2)

строго соответствует условию существования

матрицы с диагональным преобладанием в любом

ортонормированном базисе, соответствующем

оператору А.

w ( A ) <. ---- , n * 1

^V ’ V n - 1

3. Вычисления опровергают факт существования диагонального доминирования у матрицы, определяющей суть задачи. В качестве примера такого сорта матриц можно назвать платежную матрицу в разделе линейного программирования [2]. Рассмотрим случай, в котором устроитель игры обозначает некоторую область выигрышей, на основе вероятностного подхода. Далее ему нужно выстроить такие правила, которые расположат выигрыш в нужной нам области. Игра по-прежнему должна остаться содержательной, что влечет к отсутствию диагональной доминанты в платежной матрице. Сформулированное утверждение приводит к равнозначности выполнения неравенства вида

w (A) >

n

-----, n * 1 n - 1

Очевидна необходимость геометрических построений при исследовании плотности w ( A ). Формула (3) определяет условия размерности матрицы и, как следствие, число аргументов квадратичной формы ( Ax , x ):

w2 (A) n > A w2 (A)-1

Допустим, что оператор А определяет платежную матрицу произвольной игры. При

N >  1 +

w2 (A) w2 (A)-1

После того как устроителем будет получено число стратегий игры, не меняющих ее содержательности, можно будет выстраивать стратегии для каждого случая.

Неравенство (4) подтверждает, что геометрическая плотность собственных чисел достигает единицы, что соответствует наименьшему возможному значению, и ее увеличение до больших размеров приводит к отсутствию диагонального доминирования.

Заметим, что геометрический анализ функциональных особенностей такого множества существенным образом находится под влиянием различных нюансов, определенных геометрической плотностью.

Проведенное исследование экономической составляющей коммерческой организации и формализация этого исследования, с учетом конкретизации возможности использования IT-технологий, идентификация составляющих компонент, отбор предпочтений в параметрах, уточняющих эту идентификацию, подтвердил возможность построения и дальнейшей эксплуатации имитационной модели управления с использованием операторного подхода.

Рассмотрим возможность использования многокритериального подхода к выбору наиболее адекватного управленческого решения. Величина случайного показателя двух и более альтернатив f ( A ) и f ( A ) зададим, воспользовавшись функцией распределения p{f ( A r ) >  b r } = P r , p { f ( A ) >  b } = P или двумя следующими соотношениями: p^{{f (} A r ) е[ b k , b^ ] ^} = Pk и p{P, ( A , ) g[ b k , bp ] } = P ‘ , i = 0,..., T .

Через b и bⁱ обозначим i-й параметр эффективности, k = 1,..., K , а P , P_k , P_lk , P i вероятности того, что значение его в альтернативных вероятностях не превзойдет значения P или принадлежат интервалу значений.

Сравнение одинакового показателя эффективности у двух различных альтернатив допускает рассмотрение различных детерминированных величин, которые устанавливаются с использованием вероятностного подхода: b_k

V ik ^{( A} k ) = Р ^{ fi ⁽ A i ) >  ^b ik ^} = J fi ^{( x} I ^A r ) dx

-да

+да

Vik (Ak ) = P{fi (A. ) < dik } = J fi (x 1 Ar )dx bk

Значение показателя, достижение которого гарантируется, с вероятностью, не ниже априорной:

Ф k ( A k ) = ШР f i ( A ) >  К ] >  P k }

Ф k ( A k ) = d | p[f, ( A ) < d k ] >  Y }

Также, показателями могут служить моменты более высоких порядков. Полагаем, что условия Re соответствуют условиям приоритетности одной функции распределения перед другой в соответствующую сторону.

Кроме этого, в роли таких показателей могут выступать моменты распределения более высоких порядков

T                        ³

Ф к ( A r ) = * { f 1 ( A )} = £ [ mf ( A r ) - b k ] в ;

i = 1

T                       4

Ф k ( A r ) = ^ { f 1 ( A r )} = E [ mf(A r ) — b k ] Pk -

= 1

Допустим, что условия Re соответствуют условиям приоритетным предпочтениям.

Функции распределения i-го показателя эффективности соответствующей альтернативы ставим в соответствие абсолютную приоритетность относительно функции распределения этого показагеля    p{f(A) > bk}  bk}, с учетом pf (Ar) > bk } >Re p{ft(A) > bk}, в слу- чае выполнения каждого из неравенств системы:

Ф п⁽ A r ) >  Ф пХ A i ); Ф 3 qi⁽ A r ) >  Ф 3 q/ ( A );              ₍₅₎

q = 1,..., Q ₁; Ф 5 qi ( A r ) <  Ф 5 qi ( A ); q = 1,..., Q , ;

ф , i ⁽ A r ) <  ф , , ⁽ A ); Ф 4 qi ⁽ A r ) >  Ф 4 qi ⁽ A );

g = 1,..., G ₁; ф 6 q, ( A r ) <  Ф б qi ( A , ); g = 1,..., G ₂;

или p{ fl (Ar ) > bik }>-Re p{/i (Ai) > bik } с учетом p{fl(Ar) >bik} bik}, с учетом вы полнения каждого из неравенств системы:

Ф 1 , ( A r ) >  Ф 1 i ⁽ А ); Ф 3 qi ⁽ Ar ) >  Ф 3 qi ⁽ А );         ^

q = ^1,...^, Q 1 ; Ф 5 qi ⁽ A,. ) >  Ф 5 q ⁽ A , ); q = ^1,...^{, Q} , ;

Ф ₂ , -⁽ A r ) <  Ф ,, ( A i ); Ф 4 qi ⁽ A r ) >  Ф 4 qi ⁽ A );

g = 1,..., G 1 ; Ф 6 qi (A r ) >  Ф 6 qi ( Ai ); g = 1,..., G , ;

Если не выполняется хотя бы одно из условий (5)–(6), то мы говорим об условиях относительного предпочтения [3].

Сформируем комплексный показатель оценки функции распределения i-го критерия в следующей форме:

_        Q1_ ф,(Ar) = ацфц( Ar) + E «3,Ф3 i (Ar)+ q=1

Q,    __

+E а5,Ф5 i (Ar) - «, ,Ф, i (Ar) - q=1

G1

• ^- E ^a 4 Ф4 i ⁽ A r ) ^-E ^a 6 , Ф б, ⁽ A r );

g=1

G1

ф(Ar)=E a4-^4i(a) +E аФ«(Ar) -g=1

• - «„Фи (Ar ) - «1Ф (Ar ) -

• Q1     _         Q,_

• - E a3qiФзqi (Ar ) —E а5,Ф5qi (Ar q=1

Здесь

о < a < 1, о < a < 1, о < a < 1, k = 3,4,5, 6, s = q = 1,...,Qx;         - весовые s = g = 1,...,G,; s = g = 1,...,G, коэффициеты, который удовлетворяют усло- вяим нормировки:

Q1

«11 + «2 i +Ea3 qi+Ea5 qi + q=1

G1

+Ea4gi+Ea6gi= 1. g=1

Необходимо заметить, что в зависимости от формулировки исходной задачи некоторые из значений, определенных в комплексных показателях оценки функции распределения могут отсутствовать. Это достигается, в случае равенства 0 весовых коэффициентов a_ik .

С учетом того, что ф _gi ( A r ), Ф ,gi ( A r ),

Ф_§ /( A ), Ф₈ /( A ), выражены в единицах измерения конкретного показателя, то они могут быть применены в выражениях (5) – (6) после нормировки и представлены на интервале Ф pg₁ ( A r ) е [0,1] [4].

Заметим, что в зависимости от исходной постановки конкретной задачи многие из детерминированных значений в плоскости адди-тиваных комплексных показателей оценок функции распределения могут отсутствовать. Это может быть достигнуто, если положить значения соответствующих весовых коэффициентов Ой равными нулю.

В качестве комплексных критериев, наиболее объективно оценивающих эффективность альтернатив, можем использовать аддитивные показатели, представленные в следующем виде:

n

F ⁺ ( A r ) = E wp> * ( A r );

i = ¹                           (12)

f ^- ( A r ) = E w p - ( A .- );

i = 1

n где 0< w < 1, i = 1,...,n;  Vw = 1.

ii

, = 1

Альтернативе A , соответствует сформированная функциями распределения n частных показателей, имеет условный приоритет перед функцией A сформированной функцией распределения n аналогичных частных показателей только в случае выполнения следующих соотношений:

A_r > _Re A , О F ⁺ ( A_r ) >  F ⁺ ( A , );

A_r < r_c A , О F - ( A_r ) >  F - ( A , ).

Таким образом, после введения и вычисления различных оценок эффективности каждого частного показателя, а также первого шага алгоритма исключения, на основе установления фактов абсолютного предпочтения подмножества альтернатив, не принадлежащих множеству Парето, алгоритма обобщенных показателей эффективности, как частных показателей на основе выражений (5)–(6), так и обобщенных показателей для каждой альтернативы, последующие шаги алгоритма совпадают с алгоритмом принятия решений в однокритериальном случае.

Заключение

Предложенный и обоснованный, с точки зрения математической формализации, подход к принятию наиболее оптимального решения по управлению поведением коммерческой организации основанный на предварительном мониторинге экономического функционирования, представляет собой интерес с точки зрения следующих аспектов:

• 1 . возможности отождествления ключевых элементов, определяющих систему, 2. в выборе формата, характеризующего состояние интересующих элементов;

• 3 . разработке виртуальной модели, воспроизводящей поведенческие особенности моделируемой системы.