Возможности использования математических моделей для теплового контроля дефектов многослойных биметаллических пластин

Для многослойных биметаллических материалов актуальной задачей является выявление дефектов расслоения. С этой целью широко применяют различные методы неразрушающего контроля, наименее затратным из которых можно считать сравнительно простой и доступный метод активного теплового контроля. Его суть заключается в дистанционной регистрации, визуализации и анализе тепловых (температурных) полей объектов. Температура поверхности объекта неоднородна под влиянием теплофизических, геометрических характеристик, параметров тепловой нагрузки и особенностей внутренней структуры объекта. Дефекты внутренней структуры вызывают появление аномальных температурных зон на поверхности объекта, анализ которых позволяет судить о наличии неоднородностей в материале в целом или на отдельных участках.

В.П. Вавилов и В.В. Ширяев [1] показали, что экстремумы производных от температуры по любой из поверхностных координат dT/dx в точности соответствуют проекциям границ внутренних дефектов на контролируемую поверхность. На рис. 1 показан пример расчетного профиля, полученного для дефекта радиусом r d = 1 мм на глубине 0,5 мм и высоте дефекта 0,2 мм, в изделии из алюминия при импульсном воздействии теплового потока 1 МВт/м². Причем для алюминия точные оценки размеров дефекта имеют место при малых временах (τ₁) наблюдения (менее 0,01 с), в то время как при больших временах (τ₂) происходит существенное расплывание температурного отпечатка.

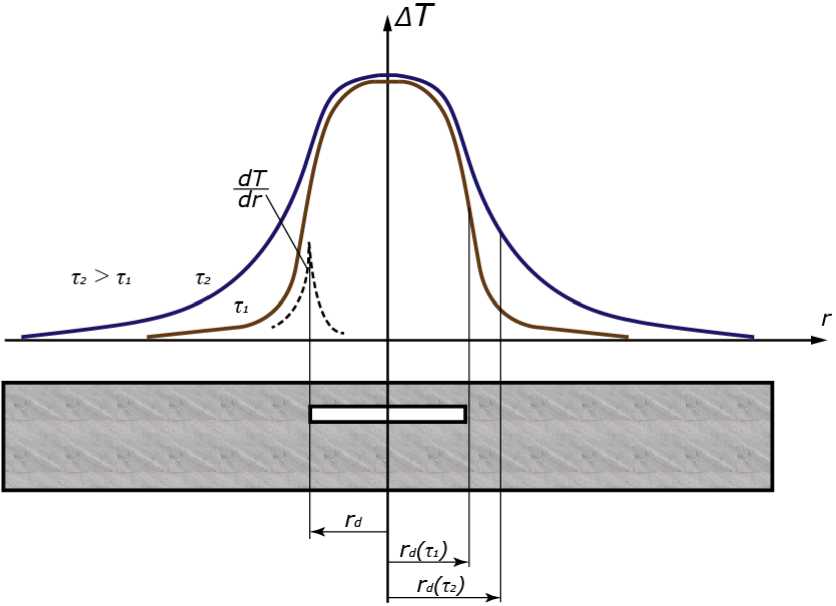
Рис. 1. Нормализованные профили температуры над воздушным дефектом в алюминиевой пластине Fig.1. Normalized temperature profiles over an air defect in an aluminum plate

Тепловой контроль (ТК) позволяет выявить различные виды дефектов: трещины, расслоения в местах сварки или склейки, поры, пустоты и раковины, нарушения изоляции, наличие посторонних включений и примесей.

Опыт исследований и практического применения ТК показывает его пригодность для контроля изделий из металлов, пластмасс и полимеров, биметаллов и композитных материалов с различными формами и качеством поверхности. Можно проводить контроль объектов без вывода их из эксплуатации или производственного процесса, используя при этом собственное тепловое излучение объекта или внешний источник тепловой стимуляции [1].

При анализе записи температурного поля (например, в виде термограммы) можно выявить участки объекта, различающиеся по температуре. Однако понять, есть ли дефект под аномальным участком и каковы его параметры, можно лишь при наличии адекватной математической модели, теоретически описывающей зависимость результатов контроля от свойств объекта и выбранных технологических режимов. В ходе построения модели расчетные результаты сравниваются с результатами натурных экспериментов, полученных при разрушении образцов. В результате обработки накопленной информации о тепловых полях постепенно формируются зависимости, позволяющие по результатам обработки термограмм не только найти дефект, но и определить его тип, геометрические параметры, например глубину залегания и пр. Таким образом, математическая модель объекта теплового контроля является неотъемлемой составляющей систем ТК.

Для одного и того же объекта или процесса может быть составлено некоторое множество математических моделей, отличающихся числом учитываемых факторов, принятых допущений, полнотой и точностью описания состояния объекта или условий протекания процесса. Одно из главных требований к модели состоит в необходимости учета всех основных факторов и взаимосвязей, существенно влияющих на рассматриваемый процесс, и исключения второстепенных факторов и связей. Набор факторов определяется достижением цели проводимого исследования, при этом всегда стремятся к упрощению модели для удобства работы с ней и снижения затрат вычислительного времени при ее практическом применении. При этом простые модели должны быть адекватными поставленной цели и должны быть теоретически обоснованы.

На практике используются стационарные и нестационарные (динамические), линейные и нелинейные, одномерные и многомерные модели. Математические модели теплообмена в сложных технических системах строятся с использованием комбинации моделей теплообмена в отдельных элементах системы. Разбиение системы на элементы (с точки зрения математического моделирования) определяется как способом внешнего воздействия, так и конструктивным исполнением системы [2].

Для однозначного определения модели теплового состояния необходимо описать ряд характеристик объекта и процесса теплообмена. К характеристикам объекта относятся его форма и материал. Геометрическую форму тела сводят к одной из шести стандартных форм (полуогра-ниченное тело, неограниченная пластина, сплошной или полый цилиндр, сплошной или полый шар) или их комбинации. Материал объекта определяется при помощи теплофизических характеристик (ТФХ). К ним относят коэффициент теплопроводности λ, теплоемкость С и плотность ρ. Также используются динамические характеристики – коэффициент температуропроводности a = X( ( C p ) и коэффициент тепловой активности, или тепловой инерции e = ^XC р , являющийся характеристикой теплового контакта.

При решении краевой задачи теплопроводности важным является правильное задание начальных и граничных условий, а также характеристик внешних источников тепла. Для моделируемого объекта иногда приходится учитывать влияние внутренних источников тепла. По характеру действия источники бывают точечные, линейные, плоские и объемные, мгновенного или непрерывного действия, постоянные или переменные во времени, а также подвижные и неподвижные. Чаще всего из условий однозначности требуется определить характеристики теплового состояния, что относится к прямым задачам теплопроводности. Для выявления дефектов внутренней структуры мы анализируем появление аномальной температурной зоны на поверхности тела и по ним оцениваем параметры размеров дефекта, в этом случае решается обратная задача теплопроводности [3].

1.    Объект исследования

Для разработки модели теплового контроля многослойного биметаллического материала с дефектами опишем свойства объекта и условия проведения измерений.

Рассматриваемый объект представляет собой трехслойную пластину, один из наружных слоев которой изготовлен из аустенитной нержавеющей стали ( 1 , h ₁), другой – из аустенитной либо ферромагнитной нержавеющей стали ( 3 , h 3 ), а между ними находится теплораспределительный слой ( 2 , h ₂) из алюминия или меди (рис. 2). Понятно, что основные теплофизические характеристики претерпевают существенные изменения вдоль направления теплового потока q изл (по нормали к слоям).

Дефекты расслоени я могут присутствовать в местах контакта наружных слоев изделия с внутренним теплораспределительным слоем с одной или другой его стороны. Не исключено наличие двух дефектов, расположенных один над другим, различного размера, с частичным или полным перекрытием. Поперечные размеры дефектов ( d , δ) ограничены и в несколько раз меньше размера пластин.

При обнаружении скрытых дефектов в большинстве случаев используют процедуры импульсного активного ТК, поскольку в стационарном режиме сигналы от дефектов нивелируются из-за выравнивания температуры по объему тела, а в условиях теплообмена с окружающей средой разность температур среды и тела не позволяет достичь достаточного значения амплитуды сигнала.

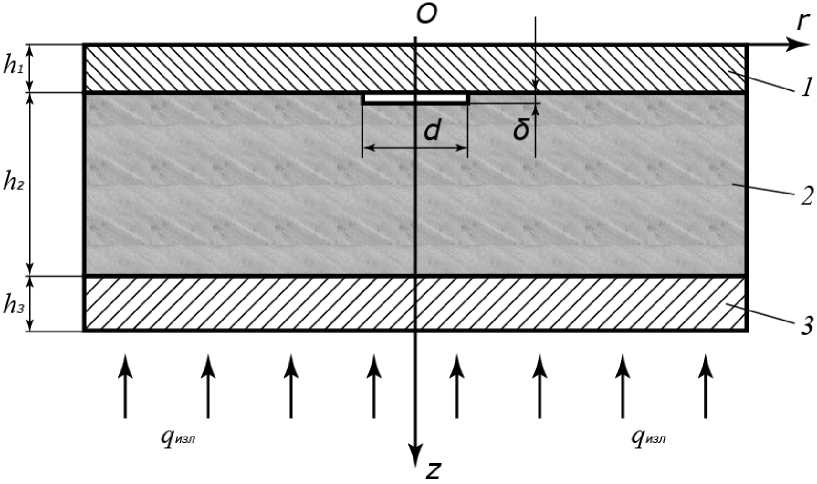
Рис. 2. Многослойная пластина с цилиндрическим дефектом, ее основные размеры Fig. 2. Multilayer plate with a cylindrical delamination, its main dimensions

В активных процедурах ТК мощность потока нагрева обычно значительно превышает мощность встречного потока теплоотдачи от тела за счет конвекции и излучения, поэтому теплообмен со стороны источника теплового нагружения можно представить как адиабатический и свести модель к более простому виду [1].

Прямой задачей является определение температурного поля с передней (нагреваемой) и обратной стороны многослойной пластины как в бездефектной области, так и с учетом различных возможных случаев расположения дефектов. При решении обратной задачи необходимо определить размеры дефектов и глубину их залегания, а также толщину и теплофизические характеристики (материал) теплораспределительного слоя.

2.    Основные допущения и ограничения математической моделитеплового состояния многослойной пластины

На основе проведенного анализа можно сформулировать требования и допущения к математической модели исследуемого объекта, показанного на рис. 2.

Для обеспечения возможности определения поперечных размеров дефектов необходимо уходить от одномерной постановки задачи.

В начальный момент времени считаем, что температура во всех точках расчетной области равна температуре окружающей среды.

Процесс нагрева должен соответствовать условиям проведения импульсного активного ТК. При этом влияние конвективной составляющей теплового потока со стороны нагрева можно учитывать только для периода остывания образца. Для выявления дефектов с обеих сторон теплораспределительного слоя модель должна учитывать условия проведения односторонней и двусторонней процедур ТК.

Контакт между отдельными слоями пластины полагаем идеальным, то есть на границе раздела выполняется равенство температур и тепловых потоков. Передачей тепла в цилиндрическом воздушном зазоре можно пренебречь.

Таким образом, при моделировании теплового состояния многослойной пластины был принят ряд допущений и ограничений.

• 1.    Для температурного поля имеет место осевая симметрия (dT/dф = 0), считаем, что температурное поле нестационарное и двухмерное – T(r, z, τ).

• 2.    Все пластины имеют форму цилиндра радиуса R, причем R >> hi.

• 3.    Передачей тепла в цилиндрическом воздушном зазоре можно пренебречь.

• 4.    Отсутствует термическое сопротивление в контакте стальной и алюминиевой пластин. Считаем, что контакт между отдельными слоями является идеальным, то есть на границе раздела выполняется равенство температур и тепловых потоков [4].

3.    Выбор математической модели

Полученные результаты применены авторами при разработке модели для трехслойной сталеалюминиевой пластины с одним дефектом в виде цилиндрического воздушного зазора.

Большинство моделей теплопроводности твердых тел базируется на дифференциальном уравнении теплопроводности параболического типа различной размерности в декартовых, цилиндрических или сферических координатах [1, 3, 5].

Большое количество аналитических решений одномерных задач нагрева (охлаждения) неограниченной пластины для расчета температур в бездефектных областях можно найти в классической литературе по теории теплопроводности [6, 7].

Одномерные модели используют при разработке систем теплозащиты, основываясь на недопустимости большой глубины прогрева теплозащитной конструкции при взаимодействии с внешней средой [2, 8]. Хорошо систематизированы классические решения для однослойной пластины в различных условиях нагрева (равномерно-распределенным тепловым потоком в виде непрерывного стационарного потока, прямоугольного теплового импульса, мгновенного импульса Дирака, а также тепловых волн) [1, 3]. При переходе к многослойным объектам применяют принцип суперпозиции [2, 3].

Запись граничных условий зависит от применяемой методики теплового контроля. В общем случае при неадиабатическом теплообмене на нагреваемой поверхности объекта контроля имеет место смешанное граничное условие II и III рода, которое выражает условие баланса трех потоков на поверхности изделия: потока нагрева, потока, уходящего в глубину объекта за счет теплопроводности, и потока теплообмена с окружающей средой за счет конвекции и излучения. При отсутствии теплообмена на поверхности (мощность потока конвекции и излучения много меньше падающего на поверхность теплового потока) условия приближаются к адиабатическим. В ТК такие условия возникают при активном тепловом контроле с импульсным нагревом и малыми временами наблюдения [9].

В многослойных объектах при переходе через границу слоев выполняются граничные условия IV рода – условия неразрывности теплового потока и температуры на границе слоев:

• . d T 5 T + i

• ^Х i =^ i + 1 д ; T i = T + 1 ^{. (1)} б Z О Z

Задача усложняется при моделировании многослойных объектов с дефектами расслоения – плоскими воздушными промежутками между слоями. Теплопередача в таких дефектах в общем случае происходит путем теплопроводности, конвекции и излучения. Однако анализ составляющих теплового потока, проведенный в [1], показывает, что в тонких дефектах (до 250 мкм) мощность потока теплопроводности существенно превышает величину потоков конвекции и излучения, тогда как с ростом толщины дефекта при его размерах 5–25 мм в нем может развиваться конвекция (при сохранении низкой мощности потока излучения). Излучение становится существенным при разнице температур между границами дефекта более 500 °С.

На границах раздела слоев рассматривают два типа ГУ. Дополнительные условия неразрывности (ГУ IV рода) формулируют при прохождении границы дефекта и основного материала. При этом распределение температуры зависит в том числе от теплоемкости слоя, поэтому такие дефекты называют емкостными. Если теплоемкостью дефектного слоя ( i+ 1) толщиной l i _{+ 1} можно пренебречь, то его основной характеристикой становится тепловое сопротивление

Ri+1, и соответствующие дефекты называют резистивными. На границах резистивных дефектов температура изменяется скачкообразно, а тепловой поток остается неразрывным:

T -+ 1 - T- = R i + 1

^{д T}i +1 .   _R _ li +1 -

;    R i + 1 =        ;

^d z              ^ i + 1

-Х,^=-хы i                 i +1

б z

8 T i + 1 б z

.

Рассмотренные зависимости и допущения реализованы в модели односторонней процедуры теплового контроля трехслойной пластины при нагреве импульсом Дирака [10]. Модель отличается тем, что внутренний слой поочередно рассматривается как слой с идеальным контактом либо как резистивный дефект между двумя слоями. Пренебрежение теплоотдачей на наружных поверхностях пластины позволяет авторам получить аналитическое решение, пригодное для дальнейшего использования в обратных задачах тепловой дефектометрии.

Трехслойная одномерная модель неограниченной пластины в неадиабатических условиях предложена для решения различных задач теплового контроля (многослойное изделие, покрытие на подложке и др.). В данной модели средний слой поочередно рассматривается либо как емкостный дефект, либо в качестве связующего материала. Модель основана на одномерном дифференциальном уравнении теплопроводности параболического типа. Граничные условия учитывают теплоотдачу на нагреваемой и обратной поверхности пластины и неразрывность тепловых потоков и температуры на границах слоев.

Авторы [1] приводят достаточно сложное аналитическое решение задачи нагрева объекта и отмечают, что расчет подобных задач для неадиабатических пластин с числом слоев более трех в аналитическом виде теоретически возможен, но практически весьма трудоемок вследствие громоздкости результатов преобразований, и в этом случае чаще применяют численные методы. При этом аналитические модели можно использовать для оценки точности численных решений в дефектных областях, для которых классические решения [6, 7] не применяют.

Также отмечено, что при наличии в теле нескольких тепловых барьеров (зон контакта различных материалов и дефектов) односторонним методом теплового контроля удается исследовать не более 2–3 барьеров, наиболее близко расположенных к поверхности нагрева. Для выявления глубоко залегающих дефектов предложено применять двухстороннюю процедуру теплового контроля (расположение источника нагрева и регистрирующих устройств с разных сторон контролируемого объекта) и соответствующим образом модифицировать математическую модель.

Для моделирования нагрева двухслойного биметаллического материала с идеальным контактом между слоями подвижным точечным источником тепла постоянной плотности разработана одномерная модель температурного поля [4]. На ее основе выполнена оценка требуемых энергетических параметров излучения источника тепла и определены толщины слоев и теплофизические характеристики биметалла.

Одномерная модель ТК многослойного объекта с термическим сопротивлением между слоями применяется для решения задачи контроля пористости металлического каркаса и измерения толщины заполняющего его фторопластового слоя [11].

При использовании одномерных моделей для решения задач дефектометрии можно определить глубину залегания дефекта и величину его раскрытия («толщину»), но невозможно определить поперечные размеры (протяженность). Многомерные модели позволяют учитывать рассеяние тепла в материале объекта вокруг дефектов и более корректно определять температурный сигнал над дефектом. При исследовании двумерной модели объекта с дисковидным дефектом для различных материалов [1] определены критические значения отношения радиуса дефекта к глубине залегания, для которых амплитуда сигнала достигает возможного максимума.

При переходе от одномерной постановки задачи к двумерной усложняются уравнения, описывающие процессы внутри материала. В качестве примера можно привести моделирование процессов активного ТК для определения дефектов в многослойных пластинах из углепластика. В первой части [12] представлена одномерная модель многослойной пластины с дефектами, для которой предложено аналитическое решение. Во второй части [13] выполнен переход к двумерной модели и используется численное решение обратной задачи тепловой дефектометрии (определение размеров и глубины залегания дефекта) с точностью порядка 10 %.

В зависимости от анализируемой задачи дифференциальное уравнение теплопроводности может быть записано в декартовых, цилиндрических или сферических координатах. Разнообразные примеры двумерных и трехмерных моделей для различных объектов ТК приведены в [1, 5].

Для одномерного и двумерного моделирования нагрева многослойных адиабатических пластин разработан метод «теплового четырехполюсника» [14, 15], согласно которому решения уравнения теплопроводности выражаются в виде линейных матричных связей между векторами температуры и тепловых потоков на границах многослойной системы, что позволяет получить решения, структура которых не зависит от граничных условий.

С применением метода четырехполюсника разработана двумерная модель сочетания дефектов, расположенных один над другим в различных слоях углепластика [16]. Показано, что сигнал от двух тонких дефектов ведет себя иным образом, нежели сигнал от одного дефекта двойной толщины. Суммарное температурное распределение Δ Т Σ ( х , у , τ) над группой малоразмерных дефектов может быть представлено как суперпозиция сигналов от каждого дефекта как в пространстве, так и во времени, Δ Т Σ ( х , у , τ) = ΣΔ Т i ( х , у , τ).

Обобщенная трехмерная модель теплового неразрушающего контроля многослойных объектов с неоднородностями предложена для оценки потерь в ограждающих конструкциях, обнаружения дефектов в металлопрокате в ходе технологического процесса, диагностики состояния изоляционного покрытия, швов и стенок труб [17, 18]. Модель основана на нестационарном уравнении теплопроводности в декартовых координатах и учитывает возможность присутствия внутреннего объемного источника тепла. Дефекты моделируются при помощи условий неидеального теплового контакта. Полученные зависимости применяются для расчета значений теоретических температур. Авторами данного способа разработан также метод решения обратной задачи для определения коэффициентов теплопроводности слоев материала контролируемого объекта и параметров геометрии дефектов [19].

Модели для многослойных пластин с дефектами расслоения весьма разнообразны, но при этом существуют общие подходы к их разработке. Набор факторов, ограничений и допущений определяется главным образом целью проводимого исследования, при этом всегда стремятся к упрощению модели для удобства ее практического применения.

С учетом сформулированных допущений будем полагать, что распределение температуры в двух стальных пластинах и алюминиевой пластине описывается уравнением теплопроводности ( т >  0, 0 <  r <  R , 0 <  z <  ( h 1 + h 2 + h ₃)) (см. рис. 2):

д T     /д² T 1 д T д ² T

= ai        +i- + дт      I дr2   r дr   дz г где i = 1, 2, 3 - номер слоя; т - время; T(r, z, т) - температура, ai = Xi /(ciрi) - коэффициент температуропроводности; Xi, рi, ci - соответственно теплопроводность, плотность и удельная теплоемкость металлов.

Индекс 1 соответствует стали при 0 <  z <  h i ; индекс 2 - алюминию при h 1 <  z < ( h 1 + h 2 ) ; индекс 3 - стали при ( h 1 + h 2 ) < z < ( h i + h 2 + h з ) .

Для решения дифференциального уравнения (4) его необходимо дополнить краевыми условиями.

В начальный момент времени считаем, что температура во всех точках расчетной области равна температуре окружающей среды (для 0 <  z <  ( h 1 + h 2 + h ₃), 0 <  r <  R ):

T ( r , z , 0) = T 0 .                                                                                            (5)

Граничные условия (ГУ)

На оси цилиндра имеем условие осевой симметрии (для r = 0, 0 <  z <  ( h 1 + h 2 + h ₃))

5 T L=0. д r

На боковой стенке многослойной цилиндрической пластины из допущения 2 имеем (для r = R , 0 <  z <  ( h 1 + h 2 + h ₃))

^дЛ- = 0. д r

На верхней стенке I пластины

Для (0 < r = R, z = 0) в период нагрева пластины имеем 0 < т < Ti граничное условие 2-го рода q изл = -^ -TS                                                                (8)

az при ее остывании т1 < т < (т1 + т2) граничное условие 3-го рода

« окр Т — t окр ) = А                                                                 (9)

оz где qизл - тепловой поток нагрева пластины путем теплового излучения; аокр - приведенный коэффициент теплоотдачи (излучением и конвекцией) от внешней поверхности стенки, имеющей температуру T1, в окружающую среду с температурой tокр .

Заключение

Рассмотрена структура математической модели теплового состояния объекта ТК. Приведено описание объекта исследования – многослойной биметаллической пластины с дефектами расслоения и процесса проведения теплового контроля. Рассмотрены математические модели подобных объектов, выполнен анализ существующих подходов к их разработке. На основе проведенного анализа сформулированы требования и допущения для математической модели исследуемого объекта и приведена математическая модель импульсного нагрева и остывания многослойной пластины при наличии дефекта расслоения.