Возможности компьютерного моделирования в экологии

EDN: FYUVPZ

Введение . В структуре реформирования высшей образовательной системы всегда фигурировала проблема компьютерной подготовки студентов и аспирантов. Поскольку для математиков, физиков, будущих специалистов в области промышленного производства эта проблема всегда решалась, то остаются гуманитарии, биологи и химики. Нужны ли экологам азы ЭВМ?

Сейчас вполне очевидно, что просто преподавать языки программирования или принципы работы ЭВМ не имеет смысла даже для биологов и химиков. Для этих будущих специалистов ЭВМ и все, что с ней связано, имеет исключительно прикладной характер. Иными словами, проблема мотивации остается открытой, особенно для биологов и экологов. Биолог, химик, эколог не понимают для чего им знания об ЭВМ, их устройстве, принципах программирования. В этой связи мы разработали курс системной экологии, к которому прилагаются программы ЭВМ и который представляет модели экосистем и отдельных популяций.

Какие это программы ЭВМ, для чего они нужны экологу, как с ними работать? Кратко представляем ответы в настоящей статье. При этом особо подчеркивается именно прикладной характер разработанного нами курса системной экологии (на базе ЭВМ).

Методы исследования. Используются уже существующие модели различных популяционных процессов. На базе этих моделей даны программы ЭВМ (на языке Basic). В среде этого языка запускаются указанные программы на ЭВМ и дается прогноз поведения экосистемы, их динамика. Используется метод Эйлера для расчета моделей. В частности, рассмотрены модели Мальтуса, Ферхюльста-Пирла, Лотка-Вольтерра, модели эпидемий.

История вопроса. Первая модель экопроцесса появилась в конце ΧVΙΙΙ в. в виде модели Мальтуса. Это была модель популяционного взрыва. В начале ΧΙΧ в. появилась модель Ферхюльста-Пирла. В данной концепции впервые внедрена обратная связь для регулирования численности популяции. В последующие десятилетия ХХ в. была удостоена Нобелевской премии за двухвидовую модель, именуемую моделью "хищник-жертва".

В конце ΧΧ в. была построена математическая теория распространения заболеваний в популяциях. Были решены задачи оптимальной борьбы с эпидемией и эпизоотией. Решена проблема устойчивости экосистем к распространению инфекционных болезней. Последние годы активно развивается компартментно-кластерная теория экоситстем (ККТЭ). В рамках этой ККТЭ решаются задачи устойчивости экосистем, проблемы их развития, изучаются эффекты действия внешних факторов на популяции животных и растений [2, 5, 6].

dx / dt = ax

Эта модель хорошо описывает популяционный взрыв. В этой модели a – биотический потенциал или скорость прироста численности популяции x(t) . Величина dx/dt (производная от x(t) ) представляет скорость такого прироста. Рассмотрим эту модель более подробно в рамках разностной модели.

dx ≈ x(N+1)

Если использовать формулу (2), то легко получить рекуррентное соотношение вида: dx ≈ x(N+1) – x(N) = a * x(N) * dt . Здесь символ * обозначает умножение. Далее легко получить ядро

В целом, математическое моделирование в экологии прошло долгий путь своего развития от конца XVIII в. и до наших дней. Особое значение уделялось двухвидовым и многовидовым экосистемам, проблемам их устойчивости (на моделях и в реалии). Очевидно, что все это составляет большой и важный раздел всей экологии. Однако, сами экологи относятся к системной экологии весьма пренебрежительно. При этом системная экология (СЭ) составляет фундамент всей экологии. Без СЭ невозможно изучение экологии, т.к. сама экология оперирует только с системами [2, 3, 6, 8].

Результаты исследований. Следует еще раз напомнить, что экология – это весьма быстро развивающаяся и новая наука. При этом она изучает только системы (популяции, биоценозы и т.д.) И поэтому без системного подхода экология просто не может существовать. В этой связи базовый ее раздел – это системная экология (с ее моделями). Отметим, что биология, зоология может изучать даже один экземпляр вида. Однако, в экологии это совершенно невозможно (популяция – это система!).

Очевидно, что без знания теории систем и системной экологии сама экология просто немыслима. Напомним, что первая модель динамики популяций возникла в конце ΧVΙΙΙ-го века. Это была модель Мальтуса, которая описывала динамику популяционного взрыва.

Фактически, это была модель неограниченного роста численности популяции x = x(t) в виде простейшего дифференциального уравнения вида:

Всегда дифференциал x(t) , т.е. dx, можно представить как разность между новым значением численности x(N+1) и старым значением x(N) . Иными словами, прирост численности популяции за малый интервал времени dt будет иметь вид:

– x(N)            (2)

уравнения (1) для точного расчета численности x(N+1) и модели (1).

Действительно имеем:

x(N+1) = x(N) + a * x(N) * dt (3)

Это уравнение (3) является рекуррентной формулой для расчета любого значения x(N+1) при пошаговых расчетах на ЭВМ. Сама программа ЭВМ для такого расчета примет вид (язык Basic):

10 CLS: SCREEN 9, 1, 0

20 INPUT «К=», К: INPUT «DT=», DT: INPUT «NO=», NO: INPUT «C=», C: INPUT «T=», T

30 NS = (N0 ^ 2 / C + 1 / T) * DT

40 FOR I = 2 TO K

50 NN = NS + (N0 ^ 2 / C + 1 / T) * DT

60 X = I * dt + 50: Y = 300 - NN

70 PSET (X, Y), 14

80 LET NS = NN

90 NEXT I

100 LINE (50, 300)-(500, 300), 12: LINE (50, 300)(50, 20), 12

110 LOCATE 22, 8: PRINT «time year»

120 END

Где, К – параметр цикла; DT – временной интервал; N – численность; С – системная постоянная.

Из этой программы легко увидеть, что ЭВМ не только считает численность популяции (пошагово с шагом dt ), но и строит график зависимости x = x(t) в прямоугольной системе координат. Студенту предлагается набрать эту программу и смоделировать x(t) . На рис. 1. дан график модели (1), в которой можно изменить величину a и наблюдать динамику x(t) .

Рис. 1. Модель популяционного взрыва (Population explosion model)

Подчеркнем, что это будет одновидовая модель популяционного взрыва, которую предложил Мальтус в конце 18-го века. Имеется еще одна одновидовая модель численности популяции с лимитированием. В этом случае мы имеем обратную связь в виде элемента –bx в правой части модели вида:

dx / dt = (a – bx)x                (4)

Легко видеть, если нет обратной связи, то мы имеем модель Мальтуса ( b = 0 и (4) переходит в (1)). Однако, модель (4) уже не имеет неограниченный рост (как в модели (1), где x (t) = x 0 exp(at) ). Модель (4) представляет лимитирование и легко найти ее предел.

Для этого мы задаем нулевую скорость прироста численности x(t) , т.е. получим dx / dt = 0 . В этом случае (a – bx)x = 0 и легко найти это предельное число x* . Действительно, мы получим 0, если x = 0 (это не интересно) или при a – bx* = 0 , второй сомножитель. Очевидно, что x* это асимптота, что представлено на рис. 2.

В этом случае x = x* = a / b , т.е. это и есть предельное значение численности популяции (это максимум для x = x* ). В этом случае популяция достигает своего максимального значения и дальше уже не растет. В уравнении (4) мы можем найти решение задачи оптимального сбора урожая ( dx / dt = max ).

В этом случае мы получим максимальный прирост самой скорости прироста численности, т.е. d(dx / dt) / dx = 0 . В математике это называется точка перегиба. В этой точке тоже скорость продукции популяции будет максимальной. Найдем ее.

Рис. 2. Модель динамики популяции с лимитированием (Population dynamics model with limitation)

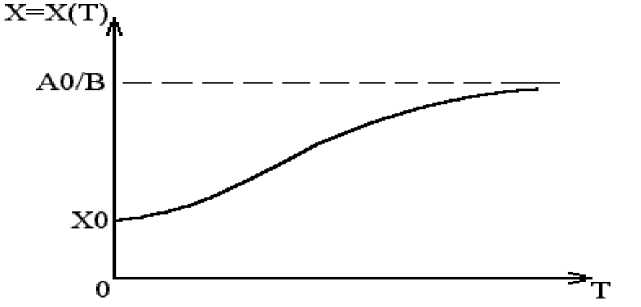
Для этого возьмем производную по x от выражения (a – bx)x = 0 . Очевидно, что такая производная дает a – 2bx m = 0 . Откуда x m = a / 2b . Это точка на графике x = x(t) , который представлен на рис. 2. В этой точке скорость прироста dx / dt будет максимальной, а затем прирост падает

Программа расчета x(t) для модели (4) имеет вид:

10 CLS: SCREEN 12

20 INPUT «К=», К: INPUT «DT=», DT: INPUT «Т1=», Т1: INPUT «C=», C: INPUT «T=», T: 30 INPUT «М=», М

40 NS = С / ((T1 - T) ^ 2 + М^2) * DT

50 FOR I = 2 TO К

60 NN = NS + С / ((T1 - T) ^ 2+ М^2) * DT

70 Т = I * DT + 10: Y = 330 - NN

80 PSET (Т, Y), 14

90 LET NS = NN

100 NEXT I

110 LINE (50, 300)-(500, 300), 12: LINE (50, 300)(50, 20), 12

120 LOCATE 22, 8: PRINT «time year»

130 END

Где, К – параметр цикла; DT – временной интервал; N – численность; С – системная постоянная; Т 1 – опорное значение времени (момент времени).

Обычно в природе различные виды взаимодействуют друг с другом. Одна из таких моделей была достаточно хорошо изучена математиками Лотка и Вольтерра. Это модель «хищник-жертва» вида:

dx 1 / dt = (a 1 – b 2 x 2 )x 1 dx 2 / dt = (–a 2 + b 2 x 1 )x 2

В этой модели x1 = x1(t) представляет численность жертвы, которую поедает хищник со скоростью –b1x2. Численность хищника x2 = x2(t) убывает со скоростью –a2, но увеличивается за счет жертвы со скоростью +b2x1.

Очевидно, что это уже двухвидовая модель и ее рекуррентная формула имеет вид:

x1(N + 1) = x1(N) + [(a1 – b1 * x2(N)) * x1(N)] * dt x2(N + 1) = x2(N) + [(–a2 + b2 * x1(N)) * x2(N)] * dt    (6)

Отметим, что в этой модели можно строить и фазовые портреты этой модели в координатах x 1 и x 2 . В этих портретах отсутствуют координаты времени. Фазовые траектории модели (6) имеют вид замкнутых линий.

В рамках такого подхода можно моделировать эпизоотии, например, в виде модели распространения заболеваний в одновидовой популяции вида:

dx / dt = ax – bxy + c 2 y dy / dt = bxy – c 1 y

В модели (7) x(t) – это численность здоровых   в x1(t) со скоростью + c2y. Модель (7) это однови- экземпляров, а y(t) – численность заболевших.  довая модель.

Последние могут выздоравливать и возвращаться

Существуют компартментно-кластерные модели, которые описывают целые экосистемы (много взаимодействующих видов). Простейшая трехвидовая модель имеет вид системы трех дифференциальных уравнений:

dx 1 / dt = a 1 x 1 + a 2 x 2 +a 3 x 3

dx 2 / dt = b 1 x 1 + b 2 x 2 + b 3 x 3                      (8)

dx 3 / dt = c 1 x 1 + c 2 x 2 + c 3 x 3

В таких моделях могут быть обратные связи и нелинейные члены, что описывается в общем виде в матричной форме:

dx/dt = A(y)x – bx y = F(x)

Здесь уже x – это вектор состояния экосистемы, y = y(t) некоторая функция ограничения (например, по трофике).

Выводы . Компьютерная грамотность экологов должна иметь высокую мотивацию для познания и обучения. В этой связи был разработан курс системной экологии. Его краткую основу мы представили в настоящем исследовании.

В этом курсе системной экологии мы подробно рассматриваем азы моделирования од- но-, двух- и многовидовых экосистем. Обсуждаются задачи оптимального сбора урожая, а также дается введение в теорию эпидемии и многовидовые компартментно-кластерные модели. Важно отметить, что все эти модели с помощью метода Эйлера переводятся в разностные модели. Ядро таких моделей входит уже в программу на ЭВМ, которая позволяет описывать динамику популяций и экосистем.

Valery M. Eskov Doctor of Physical and Mathematical Sciences, Doctor of Biological Sciences, Professor, Chief Researcher, Head of the Department of Biocybernetics