Возможности математического моделирования процесса прессования порошков при изменении коэффициентов в исходном уравнении

При производстве изделий из порошкообразных материалов, в том числе и пустотелых, осуществляется прессование полуфабрикатов [1]. В настоящее время не существует прямых методов экспериментальной оценки качества получаемого при прессовании полуфабриката, причём в первую очередь невозможно выполнить экспресс-анализ на основе экспериментальных исследований распределения плотности ρ в горизонтальном и вертикальном сечениях прессуемого образца, так как это распределение зависит от многих факторов, в том числе и от способа прессования. Если бы имелась возможность определения этих данных, то они бы позволили судить о прочности полученных полуфабрикатов ещё до начала процесса термообработки, а также давали бы возможность проектировать пресс-формы с возможностью управления этими параметрами.

Рассмотрим процесс прессования порошкообразной смеси в пресс-форме в одномерной постановке, как в [2]. При этом учитывается направление приложения силы прессования вдоль оси x . Предполагается, что в остальных сечениях, перпендикулярных этой оси, распределение плотности остается постоянным. Порошкообразная смесь в пресс-форме представляет собой вязкоупругую среду, описываемую уравнением:

_,  ,   „ ду    б 2 у

P (x, t) = E — + n —— дx     дxдt,             (1)

где P ( x,t ) – давление в сечении x в момент времени t ; ψ – сжатие смеси в сечении x в момент времени t ; E – модуль упругости смеси; η – коэффициент динамической вязкости смеси.

Из уравнения движения единичного слоя смеси ∂ x с учетом уравнения вязкоупругой среды следует выражение вида [2]:

„ д² ш    5 3 w   f L( „6^ д v    д ² ш

E—т + П—Г- + —I E— + П—- I = P—t дx2    дx 2дt   R (  дx    дtдx )    дt2

где f – коэффициент трения смеси о стенки пресс-формы; ζ – коэффициент бокового распора порошкообразной смеси; R – гидравлический радиус пресс-формы; ρ – плотность данной смеси.

После преобразования с использованием следующих обозначений Э ² = E /p; v = n/p и

2 a = fZ/R , уравнение (2) примет вид:

₂ д ² v д V _о д^   д ² у  д ² v  _п

Э² —^- + v—^-7 + 2а(Э2 —+ v —-)-- ^- = 0

д x ²      д tдx ²           д x    дtдx    дt ²      , (3)

где v – коэффициент кинематической вязкости.

Необходимо отметить, что уравнение (3) является линеаризованным и не учитывает конвективный член в исходном уравнении движения. Одна из упрощенных моделей исследования нестационарных процессов в вязкоупругой среде с учетом внешнего источника воздействия может быть основана на использовании неоднородного уравнения, т.е. источник может быть описан в правой части уравнения (3). В нашем случае удобнее описывать исследуемые процессы с помощью однородного дифференциального уравнения (3), но при установлении нестационарного условия на одной из границ в случае одностороннего прессовании порошкообразной смеси.

Для учета внешнего воздействия на порошкообразную смесь при перемещении штампа h ₁( t ) под воздействием усилия прессования и вызывающего сжатие ψ₁( t ) смеси, изменяющегося во времени по S-образной характеристике, нестационарное условие на границе можно представить в виде уравнения [2]:

V 1 ^{( t} ) = v 0 ( 1 ^- ( 1 ⁺ t / ^T 0 ) exp ( ^- tf ^T 0 )) , (4)

где т0 - постоянная времени, характеризующая процесс изменения ^ во времени; у0 — максимальное сжатие смеси.

Плотность смеси р при прессовании вдоль координаты x для любого момента времени ti можно определить через относительное сжатие d^/Zdx согласно зависимости p = po(1—а^/5x)

где р0 - начальная плотность засыпки пресс-формы.

При нулевых начальных условиях граничные условия при одностороннем прессовании следующие:

на x । H 0 : ^( t )=0;                (6)

на x 2 =0: у( t )= V i ( t ),              (7)

где H ₀ - граничная высота; ^_i( t ) - функция, учитывающая характер изменения сжатия смеси на границе перемещения штампа.

При двухстороннем прессовании порошков граничные условия следующие:

на x i = H ₃: у( t )= V i ( t ), (8) на x 2 =0: v( t )= V i ( t ), (9)

Кроме того, при одинаковых усилиях прессования в силу симметрии задачи граничные условия (8) и (9) можно свести к условиям (6) и (7), но при x 1 = H ) /2.

Решение краевой задачи в виде уравнения (3) с учетом начальных нулевых и граничных условий (6) и (7) или (8) и (9) можно получить одним из численных методов. В данной работе используется метод конечных разностей, так как он является более универсальным и позволяет решать краевые задачи, описываемые уравнениями в частных производных для неодномерных процессов. Согласно методу конечных разностей разбиваем граничную высоту H ₀ на отрезки x i = ih , время взаимодействия t на к малых шагов т. Здесь h и т - соответственно шаг по координате x и времени t ; i и k - целые числа. Дискретизация по времени является трехслойной. Краевая задача относительно у при начальных нулевых и граничных условиях (6) и (7) с учетом зависимости (3) в дискретной области Q h _т в операторной форме имеет вид:

⁹ L xx V ik ^{+ v} LtL xx Ж ik ^{+ 2 а (} Э L x ^V ik + ^v LL x V ik ) = Ln V ik

L h t V ⁽ h ^{T )} - J

V ik = ^{0 (} x i , t k ) ^e x i. ,                                ;

V ik = V 0 ^{( 1 -( 1 +} t / ^T o ^{) ex}P^{( -} t / ^T o ) )   ⁽ x, t k ) ^G x 2

⁽ x i , t k ) ^eQ h T.

;

Здесь L xX= d² d x ², L t =d/d t , L x =d/d x , L tt = d²Zd t ², x i = H ₃, x 2 =0.

Соответственно записывается в операторной форме система, аналогичная системе уравнений (10), но с учетом зависимостей (8) и (9). В данной работе, учитывая монотонно нарастающий характер процесса изменения ^(t) на границе x2, численные расчеты выполнялись с использованием явной разностной схемы и схемы Дюфорта-Франкела («ромб»). Искомое значение функции у в узле i для момента времени к+i определялось следующим образом:

^v k ^{+ 1} = [ ^{( 2 v} k -^V k ¹ V ^т ' ^{+9 2 (v} k + i - 2 ^V k + ^v k - i У h ^{2 -v (v} k + i - ^{2 v} k + ^v k - i У h ² • ^v k /^т+

+ ^{2 a(}9 ^{2 (}V ^k + i ^- V ^k У ^{h - v (}V ^k + i - V ^k У ^h • V ^k /^{т )} 1/

/[V T ^{2 -v(}V ^k + i ^{- 2} V ^k +V ^k - i y^{( h 2 t)- 2 av(V k} + i ^-V ^k У( ^{h t)} ].

Расчетная формула для P(x,t) = EdV + n^ dx    dxdt в узле i для схемы «ромб» отличается от уравнения (11) тем, что она основана на замене в симметрично-разностной схеме удвоенного значения функции ^i в момент времени tk суммой значений функций ^i в этом же узле, но на разных временных слоях tk-i и tk+i. Численные расчеты выполнялись с учетом некоторого обобщенного условия устойчивости типа Куранта для явных схем в виде т< h(N • VEРо)

(i2)

где N - постоянный коэффициент, который определялся при вычислениях.

С помощью вычислительного эксперимента оценим возможности математической модели исследования процесса прессования порошков с учетом геометрических соотношений пресс-формы и применяемых вкладышей, а также при изменении в исходном уравнении (3) коэффициента 2α с учетом того, что он пропорционален произведению коэффициентов трения смеси о стенки пресс-формы и бокового распора смеси и обратно пропорционален гидравлическому радиусу пресс-формы. На рис. 1 и 2 представлены результаты численных расчетов для плоско-параллельных моделей процесса прессования образцов из порошка, полученные при t^^ на основе решения уравнения (3) с учетом начальных и граничных условий и дополнительной координаты y. Приложение силы прессования осуществляется вдоль вертикальной оси x сверху вниз. Для получения более точных решений этих уравнений при меньшем числе итераций можно применить разработанный алгоритм, использующий изменения направлений обхода. В результате достигается существенное уменьшение искажений, вносимых расчетной схемой, и при этом уменьшается количество итераций. В расчетах плотность исследуемых образцов определялась вдоль координаты x с учетом формулы (5).

Для образца 1, соответствующего плоскопараллельной модели с вкладышем по центру пресс-формы: Н= 0,220 м; ширина L= 0,210 м (вдоль координаты у ). Остальные исходные параметры вычислительного эксперимента неизменны, кроме 2a=fZ/R (2a i = 5,76 м^-1, 2а₂ = 2,88 м^-1, 2а₃ = 1,44м^-1), причем коэффициент 2а₂ определен с учетом исходных параметров.

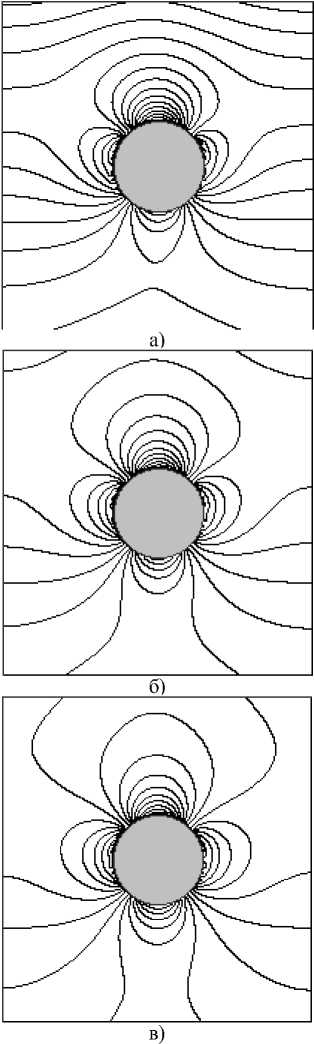
Рис. 1. Распределение изолиний приращения плотности в исследуемых образцах: а) 2а₁ 5,76 м^-1, б) 2а₂ = 2,88 м^-1, в) 2а з = 1,44 м^-1

Результаты численного моделирования исследуемого процесса при изменении в исходном уравнении коэффициента 2а i показаны на рис. 1.

Кроме того, показано распределение изолиний приращения плотности в исследуемых образцах с заданным шагом А р . С учетом закона подобия и размерности, изменение величины p i приведено к безразмерному виду: p i = р i / р m , где р m - максимальная плотность образца после прессования; р i - плотность образца в i-ой его точке. На рис. 1а представлены поля распределения изолиний приращения плотности с заданным шагом А р = 0,02 для 2а₁ = 5,76 м^-1; затем на рис. 1б и рис. 1в соответственно для 2а₂ = 2,88 м^-1 и 2а₃ = 1,44 м^-1.

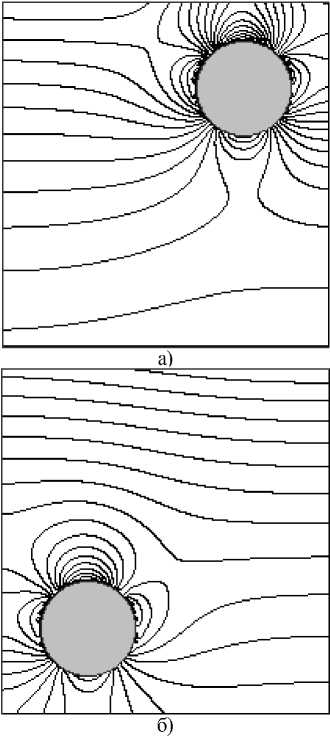
Рис. 2. Распределение изолиний приращения плотности в исследуемых образцах: а) асимметричное смещение вкладыша относительно центра вверх; б) асимметричное смещение вкладыша относительно центра вниз

Анализ результатов численных расчётов, представленных на рис. 1, показывает, что в образцах с вкладышами по центру пресс-формы с изменением коэффициента 2αi с учетом того, что он пропорционален произведению коэффициентов трения смеси о стенки пресс-формы и бокового распора смеси и обратно пропорционален гидравлическому радиусу пресс-формы, происходит изменение плотности по высоте. При этом с увеличением коэффициент 2аi увеличивается изменение плотности по высоте, однако в горизонтальной плоскости оно становится более равномерным для данных параметров. Для образца 2 (плоскопараллельная модель с асимметрично смещенным вкладышем относительно центра): H=0,220 м; ширина L=0,210 м (вдоль координаты y). Остальные исходные параметры при численных расчётах неизменны. На рис. 2 представлены поля распределения изолиний приращения плотности с заданным шагом Δρ*=0,02 для образцов с асимметричным смещением вкладышей относительно центра вверх и вниз.

Анализ результатов, представленных на рис. 2а, показывает, что для образца, имеющего цилиндрический вкладыш в верхней части, наблюдается максимальное неравномерное распределение плотности в образце вблизи граничных поверхностей. При дальнейшем обжиге данного образца это может привести к его разрушению или к появлению в нем трещин вблизи граничных поверхностей. В отличие от образца на рис. 2а в другом образце на рис. 2б наблюдается относительно равномерное распределение плотности [3]

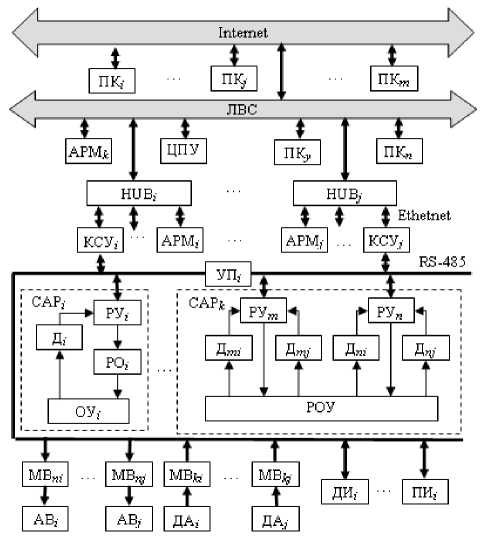
Рис. 3. Блок-схема АСУТП производства изделий из порошкообразных материалов

Реальные значения коэффициентов математической модели предлагается определять и корректировать в процессе производства на основе опытных данных. Для получения такой информации необходимо использовать современные подходы автоматизированного мониторинга исследуемых процессов на базе автоматизированных систем нижнего уровня, входящих в состав многоуровневой автоматизированной системы управления технологическим процессом (АСУТП) производства изделий из порошкообразных материалов [4]. Структура АСУТП (рис. 3) среднего и верхнего уровней содержит контроллеры среднего уровня КСУ i , … КСУ j , связанные с контроллерами регулирующих устройств РУ _i , …, РУ _n нижнего уровня на основе интерфейса RS-485, устройства для «разветвления» сигналов в сегменте сети HUB i , …,

HUB j . С учётом территориально-распределённого оборудования при производстве керамических изделий в АСУТП используется интеграция различных сетей, например, на базе RS-485 и технологий Ethernet локальной вычислительной сети (ЛВС). В структуре системы имеются автоматизированные рабочие места (АРМ) специалистов предприятия АРМ k и операторов управления распределёнными объектами АРМ i ,…, АРМ j (туннельным сушилом, туннельной печью, гидравлическим прессом и др.), центральный пульт управления ЦПУ на базе сервера с АРМ диспетчера, персональные компьютеры ПК y ,…, ПК n в сети ЛВС и персональные компьютеры ПК _i ,…, ПК _m в сети Internet с учётом возможного удалённого доступа к информации АСУТП и др.

Структура АСУТП нижнего уровня содержит следующие элементы, входящие в состав локальных систем автоматического регулирования САР i ,…, САР k (см. рис. 3): датчики технологических параметров Д i , …, Д nj , объекты управления ОУ i (например, для процесса производства шамотного огнеупорного кирпича – это туннельное сушило, туннельная печь, гидравлический пресс двойного действия (РОУ) и др.), регулирующие устройства РУ i , …, РУ n на базе контроллеров, регулирующие органы РО i . В автоматизированной системе предусмотрено управление типа старт/стоп агрегатами или оборудованием АВ i ,…, АВ j системы через модули ввода/вывода аналоговых и/или дискретных сигналов МВ ni , …, МВ nj , а также применение автоматизированной системы мониторинга на базе аналоговых датчиков технологических параметров ДА i ,…,ДА j через модули ввода/вывода аналоговых сигналов МВ ki , …, МВ kj , «интеллектуальных» датчиков ДИ i и «интеллектуальных» измерительных приборов ПИ j и др. В структуре АСУТП на нижнем уровне используется промышленная сеть на основе RS-485, в которой установлены усилители-повторители сигнала УП _i .

На нижнем уровне АСУТП для исследования особенностей процесса прессования изделий из порошкообразных смесей в структуру САР k включаются дополнительные датчики для экспериментальных исследований в виде быстродействующих оптических линейных энкодеров ДИ _k и датчиков давления ДИ m типа «Метран-150». Датчики давления ДИ m входят соответственно в контуры регулирования РУ _m верхнего прессующего механизма и контуры регулирования РУ n нижнего прессующего механизма гидравлического пресса. Эти датчики установлены в гидравлических системах низкого и высокого давления соответственно для перемещения верхнего и нижнего штампов. Линейные энко-деры ДИ k установлены с учетом перемещения верхней траверсы со штампом и прессующей траверсы с нижним штампом относительно неподвижных колонн гидравлического пресса. Первичная информация с линейных энкодеров ДИ k и датчиков давления ДИ _m , являющихся датчиками «интеллектуального» типа, поступает в систему автоматизированного мониторинга АСУТП.

Экспериментальные исследования в натурных условиях на базе автоматизированных систем нижнего уровня АСУТП на основе «интеллектуальных» датчиков технологических параметров, осуществляющих непрерывно или с минимальным интервалом усреднения измерение параметров процесса, а затем с помощью контроллеров КСУ, осуществляющих в заданном цикле интервала усреднения круглосуточный сбор измерительных данных с этих датчиков, накопление, обработку и передачу их в систему автоматизации, будет получена информация, необходимая для углублённого исследования формуемых с помощью гидравлических прессов керамических изделий из порошкообразных смесей, а также для определения и коррекции коэффициентов в уравнении (2). Рассматриваемый способ определения плотности изделия при прессовании порошков легко распространяется на двухмерный или трехмерный случай для определения плотности образца по различным сечениям с целью оптимизации формы пустотелых изделий, имеющих пустотность порядка 22-25%, а также для оптимизации места расположения вкладышей.