Возможности математической модели определения поля распределения плотности в образцах из порошкообразных смесей

• •    возможно применение её для определения картины распределения плотности в одномерной постановке с учётом начальных нулевых и граничных условий, что позволяет судить об особенностях реально формуемых изделий из порошкообразных смесей, причём с учётом различных (виртуальных) видов прессования и допущении о возможности запрессовки воздуха;

• •    возможно развитие её для исследования формующих полостей штампов для процессов прессования керамических, силикатных или ферритных изделий различного типа из порошкообразных смесей с учётом выбора рациональных размеров;

• •    возможно развитие её для исследования особенностей в процессах формования изделий из различных смесей с учетом применения различных типов технологических вкладышей, закладных деталей и др.

Постановка задачи. Рассмотрим математическую модель определения поля распределения плотности в образцах из порошкообразных смесей на основе вычислительных экспериментов при двухстороннем прессовании смеси и с учётом расположения в нижней части пресс-формы закладной детали цилиндрической формы, если при прессовании принимается за основу перемещение штампа, вызывающего сжатие этой смеси. Рассмотрим особенности процесса при двухстороннем прессовании смеси (см. рис. 1). Обозначения на схеме следующие: верхний штамп 1, каретка 2, матрица 3, нижний штамп 4, порошкообразная смесь 5, клапан обратный КО1 в гидравлической системе ГС пресса. Последовательность основных операций этого процесса следующая. В исходном положении в условиях процесса прессования изделий верхняя траверса со штампом 1 находится в крайнем верхнем положении (см. рис.1, а). В этой позиции каретка 2 выполняет двойной ход и заполняет пространство формы между нижним штампом 4 и матрицей 3. После этого верхний штамп 1 движется вниз и предварительно уплотняет смесь (см. рис.1, б). Затем происходит первое удаление воздуха из смеси и начинается предварительное прессование (при подъёме верхнего штампа 1 и его фиксации одновременно начинается выдвижение нижнего штампа 4, причём это происходит относительно медленно). Предварительное прессование порошка осуществляется нижним штампом (см. рис.1, в). Затем происходит второе удаление воздуха из смеси и наступает окончательное прессование смеси нижним штампом 4 (см. рис.1, г).

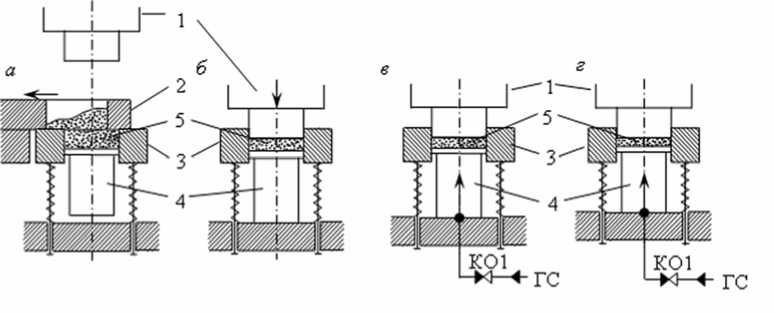
Рис. 1. Схема процесса прессования порошкообразной смеси на базе гидропресса: а - заполнение формы; б - уплотнение смеси; в - предварительное прессование смеси; г - окончательное прессование смеси

Рассмотрим особенности процесса прессования порошкообразной смеси в пресс-форме в одномерной постановке. При этом учитывается направление приложения силы прессования вдоль оси x . Предполагается, что в остальных сечениях, перпендикулярных этой оси, распределение плотности остается постоянным. Процесс прессования порошкообразной смеси в пресс-форме в одномерной постановке с учётом уравнения движения единичного слоя смеси dx и уравнения вязкоупругой среды представляется в следующем виде [2]:

д² У д у

Е   + п —2

д x ²     д x ²д t

+ ^z [ e ' + ,  ' 1 = РУ (1)

R (    дx     дtдx J     д 1 ²

где у - сжатие смеси порошков в сечении х в момент времени t ; Е - модуль упругости смеси; п - коэффициент динамической вязкости смеси; f - коэффициент трения смеси о стенки пресс-формы; с - коэффициент бокового распора порошкообразной смеси; R - гидравлический радиус пресс-формы; р - плотность этой смеси.

После преобразования с использованием следующих обозначений 9²=Е / р ; v = п / р ; и 2 а = fc / R , уравнение (1) принимает вид:

д²У    дУ        ду   д²у. д ² у

У     + v-      + 2 а ( У    + v-     )--= 0 , ⁽²⁾

дx     д tдx           дx    д tдx   д t2

где v - коэффициент кинематической вязкости.

Известно, что для исследования нестационарных процессов в среде под действием внешнего источника, например, давления в процессе прессования порошкообразной смеси необходимо учитывать этот источник на основе применения неоднородного дифференциального уравнения. Если источник находится на одной из границ исследуемой вязкоупругой среды, то возможно исследование изучаемых процессов с помощью однородного дифференциального уравнения (2). При одностороннем прессовании смеси и при нулевых начальных условиях граничные условия принимаются в следующем виде [2]:

на x 1 = H ₀:

у ( t ) = 0 ;                       (3)

на x2=0:

У ^{( t} ) = У 1 ^{( t} ) ,                    (4)

где H ₀ - заданная высота; у 1 ( t ) - функция, учитывающая характер изменения сжатия смеси на границе штампа.

При двухстороннем прессовании порошков граничные условия следующие (см. рис. 1): на x 1 = H 0 :

У ( t ) = У 1 ( t ) ;                   (5)

на x 2 =0:

У ⁽ t ) = У 1 ⁽ t ) ;                   (6)

Кроме того, при одинаковых усилиях прессования в силу симметрии задачи граничные условия (5) и (6) можно свести к условиям (3) и (4), но при x 1 = H 0 /2.

Считается, что внешнее воздействие ψ 1 ( t ) на порошкообразную смесь осуществляется в виде перемещения штампа, вызывающего сжатие смеси в виде некоторой S-образной характеристики на границе x 2 , которое может иметь, например, следующий вид:

V i ⁽ ) = v 0 ( 1 - ( 1 + t/ T ) exp ( - t/ т 0 )) , (7)

где т 0 - постоянная времени, характеризующая процесс изменения функции ψ 1 ( t ) во времени; ψ 0 – максимальное сжатие смеси при перемещении штампа.

Плотность ρ при прессовании с учётом координаты x для любого момента времени t i определяется через относительное сжатие д V d x в виде зависимости

Р = Р о ^{(1 -d}vl^{д x} ) , ⁽⁸⁾

где ρ 0 – начальная плотность исходной смеси в пресс-форме.

Дискретная модель. При вычислительных экспериментах используется метод конечных разностей. С учетом нестационарного процесса дискретизация по времени принимается трехслойной. На основе метода конечных разностей на соответствующие отрезки разбивается высота пресс-формы xi=ih, а также время взаимодействия t на k малых шагов τ, причём h и τ – соответственно шаг по координате x и времени t; i и k – целые числа. Для получения устойчивого вычислительного процесса при численном решении дифференциальных уравнений в частных производных разработано достаточно много методов, например, представленных в [5]. Учитывая S-образно нарастающий характер изменения ψ1(t) на границе в виде зависимости (7), расчеты выполнялись с использованием явной трехслойной разностной схемы.

Согласно методу конечных разностей разбиваем на отрезки x i = ih высоту пресс-формы, а время взаимодействия t на k малых шагов т . Здесь h и т - соответственно шаг по координате x и времени t ; i и k – целые числа. Дискретизация по времени является трехслойной. Краевая задача относительно ψ при начальных нулевых и граничных условиях (3) и (4) с учетом зависимости (7) в дискретной области Ω hτ в операторной форме имеет вид:

^ ^LXX^Vik + ^V L t^LXX ^V ik + ^{2 а} ( ^ L X ^i k + ^{v L}t^LX ^V ik ) = ^Ltt ^V ik , ⁽ x i , t k ) ^E ^ h r ;

L h r V ( ^{h T} ) - ^

V ik = 0,⁽ x i , t k ) e x i ;

V ik = V 0 ^{( 1 - ( 1} + t/ ^T 0 ) ^exP^{( -} t/ ^T 0 ) ), ⁽ x i , t k ) ^e x 2 .

где L XX =∂²/∂ x ², L t =∂/∂ t , L x =∂/∂ x , L tt =∂²/∂ t ², x 1 = H 0 , x 2 =0.

Соответственно записывается в операторной форме система при двухстороннем прессовании смеси аналогично системе уравнений (9), но с учетом зависимостей (5) и (6). Расчеты выполнялись с учетом обобщенного условия устойчивости типа Куранта для явных схем [5].

Результаты вычислительных экспериментов. Начальные и граничные условия аналогичны [2]. Результаты расчетов при двухстороннем прессовании смеси, т.е. с учетом краевых условий (5) и (6) приведены на рис. 2.

Вычислительные эксперименты по определению поля распределения плотности образца при одностороннем приложении давлении с неподвижной формой и с учётом исходных параметров приведены в [2]. Результаты сравнительного анализа данных [2] и представленных на рис. 2 показали, что характер распределения ρ более равномерен в вертикальном сечении образца при двухстороннем приложении давления, чем при одностороннем прессовании, т.е. такой метод прессования является более предпочтительным по сравнению с одностороннем прессованием, что согласуется с известными экспериментальными данными [1].

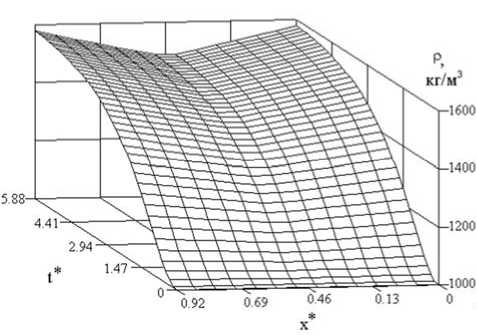
Рис. 2. Изменение плотности образца при двухстороннем прессовании

Результаты расчёта при неодномерной постановке задачи (в отличие от уравнений (1)(7)) для случая одностороннего приложения давления с учётом расположения в нижней части пресс-формы закладной детали цилиндрической формы приведены на рис. 3 и рис. 4 и представлены в относительных величинах.

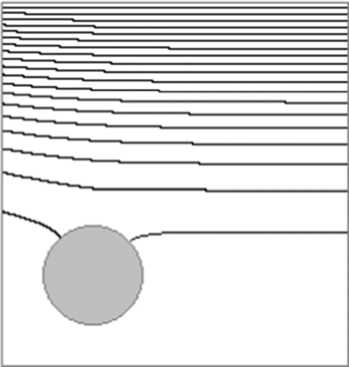
Рис. 3. Поле распределения линий равного уровня ψ *

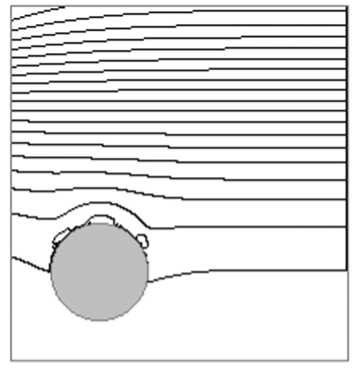
Рис. 4. Поле распределения линий равного уровня ρ *

Анализ результатов (см. рис. 4) показывает, что асимметричное расположение в нижней части пресс-формы закладной детали цилиндрической формы не приводит к существенному искажению равномерности распределения ρ * (в отличие от случая, когда закладная деталь располагается в верхней части пресс-формы, что вызывает появление областей с различной ρ * [6]). Очевидно, что отсутствие областей с существенно неравномерным распределением ρ * снижает вероятность появления трещин в образце в процессе последующей тепловой обработки.

Выводы: используемая одномерная математическая модель может применяться при исследованиях особенностей ступенчатого прессования, когда величина относительного сжатия ∂ ψ /∂ х изменяется на относительно небольшое значение или при двухстороннем приложении давления. Однако применение этой одномерной математической модели вязкоупругой среды при определении изменения плотности прессуемого образца является некорректным для синтеза оптимального алгоритма управления процессом прессования керамических или силикатных изделий из порошкообразных смесей, так как эта модель противоречит физике процессов прессования порошкообразных смесей, связанной с чередованием процессов прессования порошка и удаления воздуха из смеси, а в математической перемещение штампа, вызывающего сжатие смеси, принимается непрерывным, в виде некоторой S-образной характеристики, задаваемой на одной из границ исследуемого образца.

Рассматриваемый способ определения плотности изделия при прессовании порошков легко распространяется на двухмерный или трехмерный случай для определения плотности образца по различным сечениям с целью оптимизации формы пустотелых изделий, имеющих пустотность порядка 22-25%, при оптимизации места расположения закладной детали и др. Коммерциализация полученных результатов востребована предприятиями-производителями строительных материалов, например, в Белгородской области ООО «Объединение строительных материалов и бытовой техники», г. Старый Оскол, ОАО «Комбинат ЖБИ».