Возможности применения сквозных квантовых информационных технологий в интеллектуальных системах управления слабо формализованными физическими объектами (типа комплекс NICA)

APPLICATION POSSIBILITIES OF END-TO-END QUANTUM INFORMATION TECHNOLOGIES IN INTELLIGENT CONTROL SYSTEMS OF ILL-DEFINED PHYSICALMODEL OBJECTS (AS COMPLEX MEGAPROJECT NICA)

Korenkov Vladimir ¹ , Reshetnikov Andrey ² , Reshetnikov Gennady ³ , Ulyanov Sergey ⁴

• ¹Doctor of Computer Science, professor, laboratory director;

Joint institute for nuclear research,

Laboratory of Information Technologies;

Russia, 141980, Dubna, Moscow reg., 6 Joliot-Curie st.;

Dubna State University,

Institute of system analysis and management;

Russia, 141980, Moscow reg., Dubna, 19 Universitetskaya st.;

• ²PhD in informatics, associate professor;

Dubna State University,

Institute of system analysis and management;

Russia, 141980, Moscow reg., Dubna, 19 Universitetskaya st.;

• ³PhD, associate professor; senior researcher;

Joint Institute for Nuclear Research,

Laboratory of High Energy Physics named after V. I. Veksler and A. M. Baldin;

Russia, 141980, Dubna, Moscow reg., 6 Joliot-Curie st.;

Dubna State University,

Institute of system analysis and management;

Russia, 141980, Moscow reg., Dubna, 19 Universitetskaya st.;

• ⁴Doctor of Science in Physics and Mathematics, professor;

Dubna State University,

Institute of system analysis and management;

Russia, 141980, Moscow reg., Dubna, 19 Universitetskaya st.;

Введение: Сквозные квантовые ИТ в решении проблемы эксплуатации и устойчивого управления сверхпроводящих ускорителей

В настоящее время в физике высоких энергий особое внимание исследователей фундаментальных проблем строения материи привлекают вопросы, связанные с возникновением Вселенной и, особенно, физические процессы, происходившие после так называемого «большого взрыва». С целью проведения таких исследований в Дубне в Объединённом институте ядерных исследований (ОИЯИ) создается ионный коллайдер – Nuclotron based Ion Collider Facility ( NICA ) на энергию 4÷11 ГэВ на нуклон. Комплекс NICA включает в себя два синхротрона («Бустер» и «Нуклотрон») и «Коллайдер» – накопительное кольцо ускоренных пучков ядер с двумя местами их столкновений, в которых расположены детекторы, регистрирующие фрагменты реакций, Multi

Purpose Detector ( MPD ) – многофункциональный детектор и Spin Physics Detector ( SPD ) – детектор для исследования физики спина [1-3].

Мегапроект NICA ставит перед его участниками беспрецедентные задачи для квантовой релятивистской физики, связанные с исследованием кварк-глюонной плазмы вблизи точки фазового перехода ядерной материи². Сложность реализации такого проекта вызывает необходимость использования квантовой релятивистской информатики (КРИ) в процессах сбора, обработки и передачи данных, а также формирования физически корректной интерпретации полученных результатов. КРИ, в свою очередь, обуславливает применение сквозных квантовых цифровых технологий, GRID -технологий и суперкомпьютинга, как в решении различных в задач, возникающих в процессе реализации проекта, так и в системах управления оборудованием при его наладке и эксплуатации.

Например, чтобы обеспечить требуемые параметры в коллайдере с такой энергией, необходимо адиабатическое охлаждение пучков, как при накоплении, так и в процессе эксперимента [1-5], а сведение пучков в точку столкновения для получения необходимой светимости требует оперирования статистически большим количеством недостаточно точно определённых данных. В этом случае приходится осуществлять сбор и обработку больших потоков неоднородных экспериментальных данных и принимать решение в условиях информационного риска при формализации и установления логически непротиворечивой физической корректности и математической строгости модели исследуемого процесса.

В этом случае физическая модель объекта управления и его математическая модель относятся к т. н. слабо формализованным моделям, а корректное определение динамики объекта и управления им требует привлечения новых информационных технологий (ИТ) и методов интеллектуального управления [6, 7], позволяющих компенсировать неполное знание свойств объекта соответствующей спроектированной базой знаний в системе управления.

Отметим, что сквозные цифровые технологии – технологии, находящие свое применение в различных областях, например, рыночных секторах экономики. Официально приоритетные в РФ сквозные цифровые технологии определены распоряжением Правительства №1632-р от 28.07.2017 г., которым была утверждена программа «Цифровая экономика»: Большие данные; Нейротехнологии и искусственный интеллект; Технологии распределенного реестра; Квантовые технологии; Новые производственные технологии; Интернет вещей; Компоненты робототехники и сенсорики; Технологии беспроводной связи; Технологии виртуальной и дополненной реальностей.

Примечание . Разделение технологий на субтехнологии, приведенное в данном документе, является экспертным. В силу различий между сквозными цифровыми технологиями, невозможно применить единую классификацию внутри технологий, кроме функциональной. Однако, согласно программным документам «Национальной технологической инициативы», по мере того, как отрасли трансформируются в рынки, технологии находят свое применение в различных областях. Кроме того, сквозные цифровые технологии находятся на различных уровнях готовности и в разном сроке от выхода на плато продуктивности. Следовательно, функциональная классификация не полностью удовлетворительна в отношении сквозных цифровых технологий на данном этапе реализации плана мероприятий направления «Формирование исследовательских компетенций и технологических заделов» программы «Цифровая экономика Российской Федерации». Подчеркнем, что в мегапроекте NICA применяются практически все из перечисленных приоритетных направлений развития сквозных цифровых технологий.

Подобный проект, в котором осуществлялся процесс столкновения ускоренных протонных пучков, был успешно реализован в Европейском исследовательском ядерном центре (CERN) и позволил, в частности, коллаборации физиков из различных стран экспериментально обнаружить существование элементарной частицы (бозона Хиггса), связанной с таким свойством материи, как гравитационное взаимодействие. Одну из важнейших ролей в полученном результате сыграло применение ГРИД-технологии сбора и обработки данных, разработанной в ЛИТ ОИЯИ.

С точки зрения физики, такого рода мегаустановки относятся к классу плохо формализуемых систем, а с точки зрения теории и систем управления оптимальное управление подобного рода физическими системами сталкивается с рядом слабо исследованных проблем, и одна из них -возникновение во время проведения эксперимента нештатных ситуации. Так, например, опыт, приобретённый в ЛФВЭ ОИЯИ в результате эксплуатации первого в мире сверхпроводящего ускорителя ядер «Нуклотрон», показал возможность возникновения трудностей управления ускорительным комплексом в нештатных и непредвиденных ситуаций, возникавших в течение сеансов работы (см. рис. 1 и табл. 1):

• -    непредвиденная просадка напряжения электроснабжения, приводящая к перезагрузке компьютеров, перенастройке системы задающей электроники управляющих сигналов и других систем;

• -    нештатный переход сверхпроводящих магнитных структур в нормальное состояние с экстренной эвакуацией запасённой энергии, например, в следствие непредвиденного облучения ускоряемым пучком сверхпроводящих обмоток или появление помех, воздействующих на датчики перехода сверхпроводящих обмоток;

• -    возникновение, например, при некоторых режимах работы помех ВЧ станций, превышающих порог чувствительности системы защиты от переходов магнитов в нормальное состояние, что приводит к экстренному срабатыванию системы защиты;

• -    сбои или ошибки в работе управляющей электроники или ускоряющих ВЧ станций в связи с неисправностями (дефектами) или износом оборудования;

• -    нештатные потери и снижение интенсивности пучка при переходных режимах изменения магнитного поля ускорительного кольца;

• -    потери при транспортировке и переводе пучка между отдельными структурами ускорительного комплекса;

• -    наводки от ускоряющих ВЧ станций на пикап - электроды, диагностирующие динамику пучка, в частности, при низких интенсивностях;

• -    нештатные ситуации с охлаждающими и вакуумными системами кольца.

Нештатные ситуации

Нарушение вакуума в кольце

Спонтанные переходы в нормальное состояние магнитной оптики ■■

Collider

Потери при переводе пучка в каналы экспериментального корпуса (бустера) InlernolXrgef

Heavy Ion LinocX *

Облучение ускоряющим пучком I сверхпроводящих обмоток магйЯгной структуры

Ш-20 1

Сбой задержек управляющихсигналов в связи с (дефектами) неисправностью и износа оборудования

Переход магнитов в нормальное состояние с экстренной эвакуацией запасённой энергии и магнитного поля

Рис. 1. Нештатные и непредвиденные ситуации управления

Таблица 1. Нештатные ситуации управления

Возможные нештатные ситуации управления
«Просадки» напряжения силовой сети, вызванные внешними причинами.	Спонтанный переход СП магнитных элементов кольца в нормальное состояние с экстренной эвакуацией запасённой энергии магнитного поля.	Срабатывание системы защиты и эвакуации энергии при возникновении уровня помех выше порога чувствительности системы.
Сбой управляющей электроники в связи с неисправностью и износом оборудования: а) ВЧ станций; б) системы выработки управляющих сигналов; в) локальных источников питания аппаратуры на кольце и залах управления.	Облучение ускоряемым пучком стенок вакуумной камеры и сверхпроводящих обмоток магнитной структуры (особенно в местах инжекции и вывода пучка), вызывающее переход в нормальное состояние.	Потери интенсивности пучка в процессе ускорения при переходных процессах изменения характера нарастания магнитного поля ускорительного кольца
Наводки от ВЧ станций на пикап-электроды, затрудняющие диагностику динамики пучка.	Потери интенсивности при выводе пучка в каналы экспериментального корпуса.	Непредвиденные неисправности в криогенных и вакуумных системах.

Традиционные системы управления принципиально не учитывают возникновение нештатных ситуаций управления и не включают в контур управления человеческий фактор, что не гарантирует своевременного достижения цели управления – получение максимальной интенсивности ускоренного пучка и устойчивое повторение требуемых режимов ускорения с минимальными затратами полезных ресурсов, например, таких, как: время настройки и проведения соответствующих исследований, электроэнергия и т.п. Это связано с тем, что классические методы теории управления обладают методами синтеза и проектирования для хорошо формализованных и хорошо описанных объектов управления, функционирующих в заранее известных условиях и достаточно хорошо описанных ситуациях функционирования объекта управления.

Ситуация с достижением устойчивого управления сверхпроводящих ускорительных систем также осложняется следующими обстоятельствами: 1) Наличие эффекта не сохранения постоянства физических свойств ряда систем в течение сеанса работы ускорительного комплекса и, особенно, от сеанса к сеансу, что требует затрат ресурсов на исследование причин и настройку режимов функционирования. 2) Изменением компоновки ускорителя - замена элементов, реконфигурация и реинжиниринг структуры. 3) Работа с пучками различных ионов и ядер, что требует исследования и учёта индивидуальных характеристик. 4) Неизбежная неоднородность полей сверхпроводящих магнитных элементов структуры установки. и мн. др.

Перечисленные обстоятельства и их индивидуальные особенности предопределяют скрытность и недоопределенность параметров физических и математических моделей, и должны учитываться и компенсироваться в базах знаний интеллектуальных регуляторов. Квантовые сквозные ИТ позволяют спроектировать иерархические интеллектуальные системы управления, позволяющие перераспределить степень ответственности принятия решения об управлении такими объектами в зависимости от динамически изменяющейся ситуации.

Рисунок 2 иллюстрирует возможные источники возникновения непредвиденных и нештатных ситуаций управления в динамических системах, зависящие от особенностей объекта управления.

Для разработки эффективного управления в условиях непредвиденных (нештатных) ситуаций управления физическими объектами с не доопределенными параметрами выбрана квантовая ИТ.

Разработка сквозных квантовых технологий стала приоритетной в ведущих странах^{3, 4, 5} и привела к развитию многих смежных ИТ. В данной работе квантовые технологии на основе квантовых вычислений выбраны не случайно, так как их применение в задачах интеллектуального управления привело к решению классически алгоритмически неразрешимой задачи глобального робастного управления нелинейными объектами управления (ОУ) в нештатных ситуациях за счет обнаруженного синергетического информационного эффекта: из не робастных баз знаний (БЗ), не справляющихся с новой ситуацией управления, за счет применения квантового нечеткого вывода – КНВ (новый квантовый поисковый алгоритм самоорганизации знаний) – можно спроектировать в реальном времени робастную БЗ .

Объект управления:

Тип неустойчивого поведения

• -    Локальная неустойчивость

• -    Глобальная неустойчивость

• -    Неустойчивость по части обобщенных координат и нелинейные связи

Случайная структура или параметрические возмущения

Тип описания модели

• -    Математическая модель

• -    Физическая модель

• -    Слабо структурированная математическая и нечеткая физическая модель

Внешние случайные возмущения:

Различные типы задающего сигнала

Различные типы структур 5 традиционных регуляторов

• •  Различные функции распределения

вероятностей

• •  Функции распределения вероятностей

зависящие от времени

Система измерения:

• •    Шумы и помехи в датчиках

• •   Временная задержка съема сигнала

• •   Случайные отказы в датчиках

• -    принцип не разрушения и повышения эффективности нижнего исполнительского уровня системы управления физическим экспериментом за счет самоорганизации БЗ интеллектуального регулятора; и

• -    принцип синергизма извлекаемой скрытой квантовой информации из классических состояний спроектированных процессов управления.

Выполнение и реализация новых физических (информационно-термодинамических) принципов интеллектуального робастного управления осуществляются на основе решения следующих трех принципиальных проблем.

• А .    В первом случае, в отличие от прямой задачи (описания знаний количественными характеристиками), рассматривается решение обратной задачи теории искусственного интеллекта: извлечение, обработка и формирование знаний из количественных данных физических и логических экспериментов для разработки соответствующего уровня строгости физической модели исследуемого объекта (методами квантового глубокого машинного обучения на основе квантовых нейронных сетей и квантовых генетических алгоритмов⁶). В этом случае разработанная технология проектирования объективных БЗ на основе оптимизаторов БЗ на мягких и квантовых вычислениях исключает субъективизм экспертных оценок, обеспечивает гарантированное достижение требуемого уровня робастности интеллектуальных систем управления (ИСУ).

Б . Во втором случае рассматривается проблема разработки и физического обоснования математической модели квантового алгоритма управления самоорганизацией знаний для формирования робастных БЗ в реальном времени. Важна при этом роль прямых аналогов физических (квантовых и термодинамических) эффектов в реализации процесса гарантированного достижения качества управления на основе технологии квантовых, мягких и дробных вычислений.

При этом основное внимание уделяется описанию и интерпретации качественных особенностей биологически воспроизводимой (биоинспирированной) эволюции самоорганизации, основные компоненты которой описываются квантовыми операторами и составляют физическое содержание разработанной модели квантового алгоритма управления процессом самоорганизации. В этом случае рассматривается задача робастного управления в непредвиденных ситуациях на основе квантовых стратегий принятия решений в виде программного инструментария квантового нечеткого вывода как частного случая разработанного квантового алгоритма управления самоорганизацией знаний.

• В .    Решение третьей проблемы демонстрирует результаты применения ИТ проектирования робастных БЗ непосредственно в структуре ИСУ. При этом существуют особенности проектирования робастных БЗ для непредвиденных ситуаций управления физическим экспериментом и в условиях информационного риска для ИСУ, включающих в свою структуру оптимизаторы БЗ.

Синергизм неточной ( imperfect ) информации и синергетический эффект квантовой самоорганизации БЗ в условиях непредвиденных ситуаций основан на технологии извлечения скрытой в классических состояниях (неизмеримой в общем виде классическими приборами) квантовой информации (дополнительный информационный ресурс).

Проблема робастной (малочувствительной к изменениям внешних и внутренних условий функционирования) и устойчивой работы мегаустановок (типа NICA ) является одной из самых актуальных и трудных при эксплуатации и проведения физических дорогостоящих экспериментов на коллайдере. Применение систем управления на базе теории искусственного интеллекта является наиболее привлекательным при решении указанной и смежных с ней проблем и может гарантировать достижение поставленной цели управления, в том числе в условиях возникновения нештатных ситуаций. При применении методов систем с искусственным интеллектом сталкиваются с проблемой извлечения знаний и построения моделей физических систем по большим экспериментальным не структурированным данным, включая поиск информативных (в общем случае неизвестных заранее) признаков (задача Гровера поиска «иголки в стоге сена»).

Решение указанных и смежных задач предлагается осуществлять на основе сквозных квантовых ИТ, основанных на квантовых мягких вычислениях, и с разработкой интеллектуальных систем управления с иерархической структурой баз знаний. Применение сквозных квантовых технологий позволяет осуществить сжатие больших данных за счёт использования модифицированного квантового поискового алгоритма Гровера в распределённых вычислительных системах на ГРИД-технологии и технологиях суперкомпьютинга, проектировать робастные базы знаний интеллектуальных регуляторов, как отмечалось ранее, с применением квантового глубокого машинного обучения на основе квантовых нейронных сетей и квантовых генетических алгоритмов.

Есть все основания полагать, что интеллектуальные методы управления, основанные на классических и квантовых алгоритмах, позволят формировать оптимальные управляющие воздействия на физические процессы, связанные с формированием устойчивой динамики пучков и спиновых состояний ускоряемых ядер, а также управлять условиями сведения встречных пучков в коллайдере.

В работе обсуждается и предлагается решение задачи выбора и разработки программноаппаратной платформы верхнего уровня информационной технологии иерархического интеллектуального управления, не разрушающей существующий и реализуемый инфраструктурный программно-аппаратный уровень управления комплекса NICA .

Предварительно рассмотрим некоторые особенности проектирования систем автоматического управления такого рода сложными физическими установками.

Особенности разработки САУ сложными физическими установками с недоопределенными параметрами

Для повышения эффективности проводимых исследований на установке NICA, были выработаны соответствующие требования к элементам системы [8, 9]. На нижнем уровне управления широко применяются контуры управления с обратной связью, например, для подавления утечки постоянного тока и шумовых эффектов. Проводится модернизация узлов ускорительного комплекса и создание принципиально новых элементов установки [10-14]. Новые технологические возможности коснулись в том числе программно- аппаратной архитектуры, лежащей в основе системы управления. Стало возможным создавать децентрализованные, иерархические, сложно связные системы, группировать сенсоры и объекты управления установкой [15-19]. Применяются апробированные на зарубежных установках протоколы синхронизации оборудования [20].

В соответствии со структурой установки, задачи, которые необходимо решать при управлении ускорительными системами, решаются путём управления множеством параметров состояния структур ускорительного комплекса в различные моменты процесса ускорения [21, 22] (см. табл. 2).

Примечание. Данный перечень задач далеко не полон, и представляет лишь часть задач управления, связанных непосредственно с ускорительными отделами. Каждый из режимов требует оптимального управления набором параметров и требует от операторов компетентного представления о динамике процесса и знания физических особенностей физической установки, особенно в случае изменения компоновки ускорителя (замена элементов) или реконфигурации. Такой процесс управления не свободен от случайных факторов, например, в виде помех и непредвиденных ситуаций. Ситуация с устойчивым управлением также осложняется эффектом не сохранения постоянства параметров ряда систем в течение сеансов работы ускорительного комплекса и, особенно, от сеанса к сеансу или при изменении компоновки ускорителя – замене элементов или реконфигурации, что требует затрат ресурсов на переключение и настройку режимов.

Таблица 2. Обобщённый перечень задач управления

Установка	Задачи	Параметры и свойства управления	Типы управления
«Крион» и ЛУ-20	Образование пучка ионов	Условия в ионизационной камере Фокусирование	Ручное и полуавтоматическое
	Ускорение пучка	Частота и амплитуда ускоряющего напряжения
Канал инжекции в Бустер	Перевод пучка из линейного ускорителя в ускорительное кольцо бустера	Временные задержки управляющих сигналов	Полуавтоматиче ское
		Управлением величиной и качеством полей магнитных элементов	Ручное, Полуавтоматиче ский режим
Бустер	Захват в режим ускорения;	Управление токами магнитной системы	Ручное
		Управление полем инжекции	Ручное
	Ускорение при нарастании магнитного поля и частоты ВЧ станций;	Амплитуда и частота ВЧ Токи корректирующих обмоток магнитов	Автоматическое управление Ручное
	Перевода на «стол» магнитного поля;	Амплитуда и частота ВЧ Временная зависимость перестройки магнитного поля	Автоматическое управление Ручное
	Сохранения циркуляции пучка на «столе» магнитного поля;	Токи корректирующих магнитов	Ручное Автоматическое с ПИД -регулированием для стабилизации
Канал Бустер – Нуклотрон	Транспортировка пучка из бустера в Нуклотрон	Токи обмоток магнитной оптики Временные задержки управляющих сигналов	Ручная настройка
Нуклотрон	Захват в режим ускорения;	Управление магнитной оптикой и полем инжекции	Ручное
	Ускорение при нарастании магнитного поля и частоты ВЧ станций;	Амплитуда и частота ВЧ Токи корректирующих обмоток магнитов	Полуавтоматиче ское управление Ручное
	Перевод на «стол» магнитного поля;	Амплитуда и частота ВЧ Временная зависимость перестройки магнитного поля	Автоматическое управление Ручное
	Сохранение циркуляции пучка на «столе» магнитного поля;	Токи корректирующих обмоток магнитов	Ручное. Автоматическое с ПИД -регулированием стабилизации
Канал Нуклотрон -НИКА	Перевод пучка из Нуклотрона в ускорительное кольцо бустера	Задержка управления	Полуавтоматиче ское
		Временные задержки управляющих сигналов Управлением величиной и качеством полей магнитных элементов	Ручной полуавтоматиче ский режим.
НИКА	Сохранение циркуляции и группировки пучка в накопительном кольце. Сведение пучков в точки столкновения с высокой интенсивностью.	Подстрока ВЧ станции Токи корректирующих обмоток магнитов Временные задержки управляющих сигналов	Ручной и полуавтоматиче ский режим.

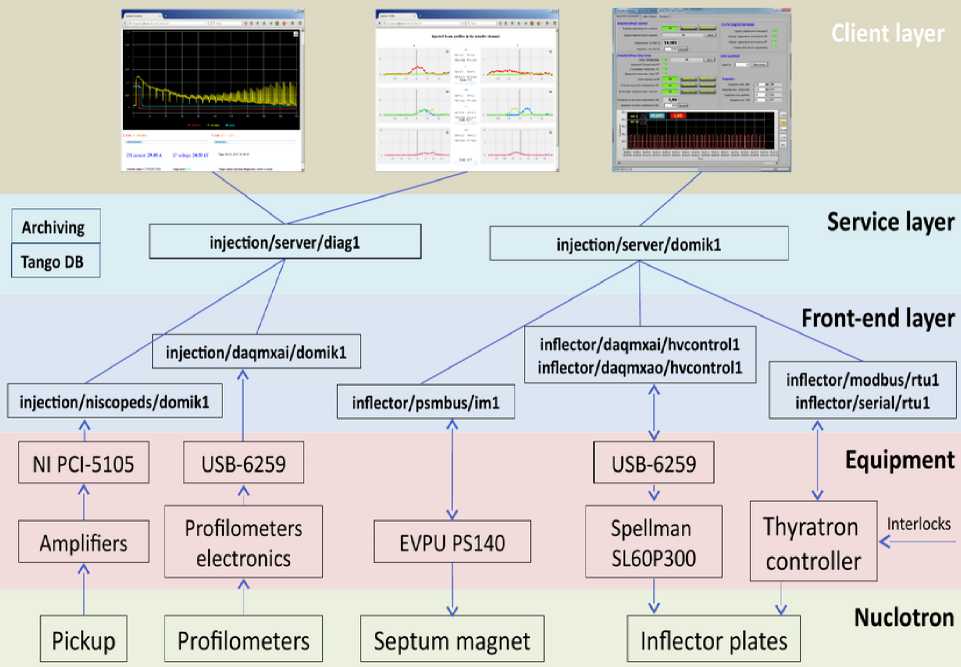
Все вышеперечисленные системы представляют собой нижний и промежуточный уровень системы управления (см. рис. 3), реализованный в виде распределенной аппаратной архитектуры, построенной на базе Tango Controls [15], которая реализует сбор, предварительную обработку, визуализацию и хранение информации.

При этом формирование сигнала на исполнительные устройства в виде управляющего воздействия возлагается на оператора - эксперта. Тем не менее, для решения задачи управления новым ускорительным комплексом может потребоваться новый подход к нелинейной динамике процессов управления. Классические системы управления, основанные на ПИД–регуляторах и нейронных сетях, не учитывают возникновение нештатных ситуаций управления, а также человеческий фактор (персонал на различных подсистемах управления объектом иногда не координирует свои действия или координирует с задержкой), что не всегда позволяет достигать цели управления при возникновении различного уровня непредвиденных ситуаций .

Несмотря на то, что технологии Tango Controls, реализует простую и быструю разработку сторонних приложении и их развёртывание, в настоящее время операторы ускорителя не обеспечены соответствующим инструментариями позволяющим вводить дополнительные качества управления – адаптацию, обучение, самоорганизацию в систему управления. Каждый раз во время запуска или реконфигурации оборудования, перевода в новое целевое состояние ускорителя, они будут проводить заново обширную настройку ускорительного комплекса.

По мере увеличения размера и сложности ускорительной техники, требования к системам управления возрастают. Машинная сложность отражается в сложности аппаратного и программного обеспечения системы управления. В то же время, программное обеспечение должно обеспечивать функционирование системы управления с более высокой степенью надежности, адаптации, обучаемости, робастности [23].

injectton/server/diagl injection/daqmxai/domikl inflector/daqmxai/hvcontroll inflector/daqmxaQ/hvcontroll

Service layer

Archiving injection/server/domikl

Tango DB

Front-end layer injection/niscopeds/domikl

Equipment

Nl PCI-5105

USB-6259

USB-6259

Amplifiers

Nuclotron

Pickup

Profilometers inflector/modbus/rtul inflector/serial/rtul

Spellman

SL60P300

Profilometers electronics

____x____

EVPU PS140

inflector/psmbus/iml --------X---

------V------

Septum magnet

V____________V.

Inflector plates

Thyratron ^interlocks controller

Рис. 3. Структура традиционной аппаратной реализацией АСУ (автоматизированной системы управления) [18]

Это очевидное следствие закона информационно – термодинамического робастного управления (см. рис. 4), соблюдение которого необходимо для проектирования структуры интеллектуальной системы управления с оптимальным распределением основных качеств управления «устойчивость – управляемость – робастность» [24, 25].

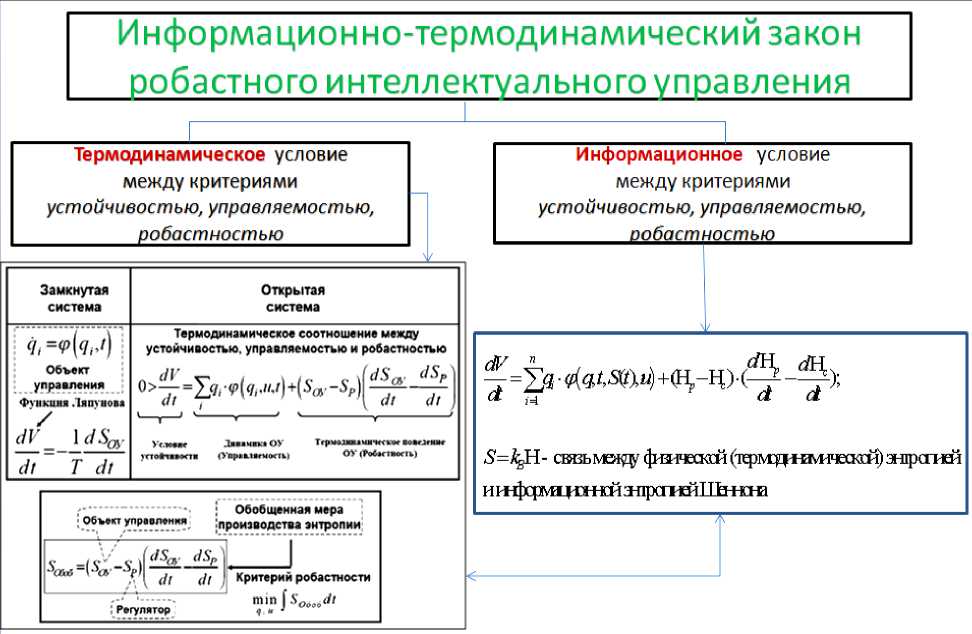
Рис. 4. Информационно – термодинамический закон робастного интеллектуального управления

Примечание . В [6,7] уточнен и дополнен физический закон самоорганизации знаний, и дан информационный анализ квантового извлечения скрытой информации. В результате количеству извлеченной скрытой в классических состояниях квантовой информации сопоставляется эквивалент в виде дополнительного производства полезной работы, которая в результате дает скрытый ресурс для совершения полезного действия, в частности достижения глобальной робастности и качества управления. В частности, выведено уравнение, которое связывает извлеченное количество скрытой информации с количеством возможной произведенной энергии, а количество произведенной энергии связано прямым уравнением с количеством произведенной полезной работы.

Отсюда следует обоснование принципа минимума требуемой исходной информации и расхода полезного ресурса. Тогда когнитивный регулятор позволяет перейти от самоорганизации к саморазвитию с обобщением уравнения на когнитивные процессы с встроенным в контур управления когнитивным регулятором. В результате возможно построить полную ИТ проектирования самоорганизующихся и саморазвивающихся ИСУ. Образовательный процесс, являющийся неотъемлемой частью разрабатываемой квантовой ИТ, основанный на извлечении новых знаний, полностью описывается данной технологией.

Обсудим особенности термодинамического и информационного законов интеллектуального когнитивного управления, являющихся базисом для реализации квантовой самоорганизации баз знаний гарантированного достижения цели управления.

Законы интеллектуального когнитивного управления и квантовой самоорганизации баз знаний

Отмечено, что свойство робастности (по своей физической природе) выступает в качестве составной части самоорганизации, а требуемый уровень робастности ИСУ достигается за счет выполнения принципа минимума производства обобщенной энтропии. Принцип минимума производства энтропии в ОУ и системе управления является физическим принципом оптимального функционирования с минимальным расходом полезной работы и лежит в основе разработки робастной ИСУ. Данное утверждение базируется на том, что для общего случая управления динамическими объектами оптимальное решение конечной вариационной проблемы определения максимума полезной работы W эквивалентно, решению конечной вариационной проблемы нахождения минимума производства энтропии S.

Таким образом, исследование условия максимума функционала max(W ) (где q, u – qi ,u обобщенные координаты ОУ и сигнал управления соответственно) эквивалентно, исследованию ассоциированной проблемы минимума производства энтропии, т. е. min(S ) .

q_i , u

Следовательно, в разработанной модели нового поискового КА используемый принцип минимума информационной энтропии гарантирует необходимое условие самоорганизации – минимум требуемой исходной информации в сигналах обучения; термодинамический критерий минимума новой меры обобщенного производства энтропии обеспечивает достаточное условие самоорганизации – робастность процессов управления с минимальным расходом полезного ресурса. Информация дает возможность совершать полезную работу (см. рис. 4).

Дело в том, что в элементы ускорительного комплекса можно рассматривать как интеллектуальную, активную многоагентную систему, где каждый управляющий элемент обладает своей интегрированной БЗ. Так, согласно [26-30], в многоагентной системе существует новый синергетический информационный эффект самоорганизации баз знаний и формирования дополнительного информационного ресурса, возникающий при обмене информацией и знаниями между активными агентами ( swarm synergetic information effect ) [26, 27]. Извлечение дополнительного ресурса в виде скрытой в классических состояниях квантовой информации осуществляется на основе квантового нечеткого вывода (КНВ), который, в свою очередь, является новым квантовым поисковым алгоритмом и частным случаем квантового алгоритма самоорганизации.

За счет синергетического эффекта создается дополнительный информационный ресурс и многоагентная система способна решать сложные динамические задачи по выполнению совместной работы. Поставленная задача может не выполняться каждым элементом (агентом) системы в отдельности в разнообразных средах без внешнего управления, контроля или координации, но обмен знаниями и информацией позволяет совершать совместную полезную работу для достижения поставленной цели управления в условиях неопределенности исходной информации и ограничений на расход полезного ресурса [27].

В частности, известно, что для систем управления с обратной связью, количество извлекаемой t полезной работы W удовлетворяет неравенству Wmaх(t) = kJ T^Icdt’^ kTIc, где к — постоянная Больцмана, Tmin (t) интерпретируется как наименьшая достижимая температура системой во времени t при управлении с обратной связью, предполагая T^п(0) = T, и Ic определяет количество информации Шеннона (перенос энтропии), извлекаемое системой из процесса измерения [29,30].

Физически синергетический эффект означает самоорганизацию знаний и создание дополнительного количества информации, которая позволяет совершить многоагентной системе максимально полезную работу с минимумом потери полезного ресурса и при минимуме требуемой исходной информации, без разрушения нижнего и среднего исполнительных уровней системы управления [7, 28, 30]. Совместно с информационно-термодинамическим законом интеллектуального управления (оптимальное распределение качеств управления «устойчивость – управляемость – робастность») проектируется ИСУ многоагентными системами, гарантирующая достижение цели управления в условиях неопределенности исходной информации и ограниченного полезного ресурса [27, 28, 30].

Примечание . Речь идет о сети слабо связанных между собой коллектива активных агентов, совместно работающих в целях решения задач, которые выходят за рамки индивидуальных возможностей. Различные узлы подобной системы, как правило, имеют различный уровень интеллектуализации (знания, алгоритмы, вычислительные базисы) и разные информационные ресурсы при проектировании. Каждый узел должен быть способен модифицировать свое поведение в 13

зависимости от обстоятельств, а также планировать свои стратегии коммуникации и кооперации с другими узлами. Здесь показателями уровня кооперации являются: характер распределения задач, объединение различных информационных ресурсов и, конечно, возможность решения общей проблемы в заданное время [31, 32].

Сложность управления комплексом NICA необходимо и возможно, по мнению авторов, компенсировать уровнем интеллектуальных вычислений, заложенных в систему управления. К таким вычислениям относятся мягкие вычисления (нечеткая логика, экспертные системы, нейронные сети, многокритериальные эволюционные алгоритмы), которые закладываются в БЗ на основе различных информационных источников (моделей и данных о реальном поведении объекта управления) и квантовые вычисления (алгоритмы поиска, самоорганизации, квантовые нейронные сети и мн. др. [30, 33]), повышающие уровень надежности и самоорганизации системы.

БЗ реализуют устойчивое повторение режимов ускорения с минимальными затратами полезных ресурсов, таких как время настройки, потеря электроэнергии, износ оборудования и криогенные расходы. Квантовый нечеткий вывод (КНВ) на основе различных БЗ, объединяет разнородные пространства поиска. Другими словами, повышение качества системы управления зависит от функций программных инструментов, которыми обладает оператор. Такие функции позволяют вводить новые сквозные информационные технологии - решения разработанные и апробированные на протяжении 40 лет в компаниях ST Microelectronics &  Yamaha Motor Co и мн. др.

Возможность применения информационных технологий, позволяющих реализовывать принципы интеллектуального управления ускорительной техникой рассматриваются уже давно [34-36].

Примечание . Более 40 лет назад начались попытки применения экспертных систем и нейронных сетей. Существуют множество решений по автоматизации ускорительной техники. Например, рассматриваются задачи многокритериальной оптимизации конструкции и компоновки самой ускорительной установки, подбора параметров управления ускорителей в различных режимах. Широкое распространением получили «нечеткие» контроллеры с интегрированной БЗ и системой логического вывода, так называемой интеллектуальной надстройкой, позволяющей заменить функции оператора по управлению системой, и ограничить его работу сторонним наблюдением за системой [37-48]. Однако большинство передовых попыток внедрения интеллектуальных технологий являются достаточно обособленными и построены таким образом, что затрудняют их тиражирование и перенос для других установок ускорителя или проектирование обобщенной интеллектуальной системы, способной гарантировано достигать целей управления в условиях неопределенности.

Особенности применения технологий мягких и квантовых вычислений в задаче интеллектуального робастного управления

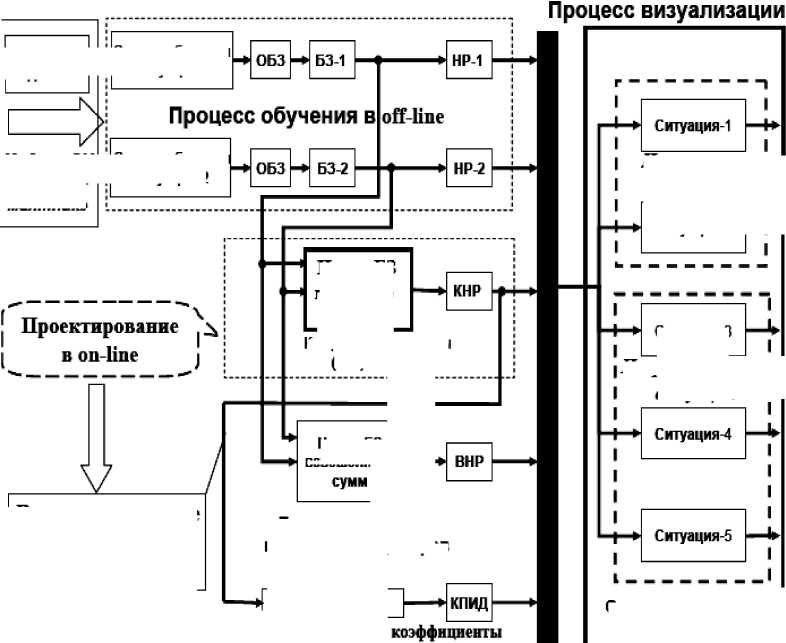
Цель эффективного использования интеллектуальных вычислений в задачах робастного управления – повышение надежности функционирования в непредвиденных ситуациях управления за счет повышения интеллектуальности нижнего исполнительного уровня традиционных систем автоматического управления (САУ). Решение задачи основано на возможности повышения робастности БЗ в ИСУ с использованием соответствующего инструментария. Информационная технология проектирования БЗ для нечетких регуляторов использует новые виды интеллектуальных вычислений и показана на рис. 5. Процесс проектирования робастных БЗ состоит из двух взаимосвязанных этапов, основанных на мягких и квантовых вычислениях соответственно.

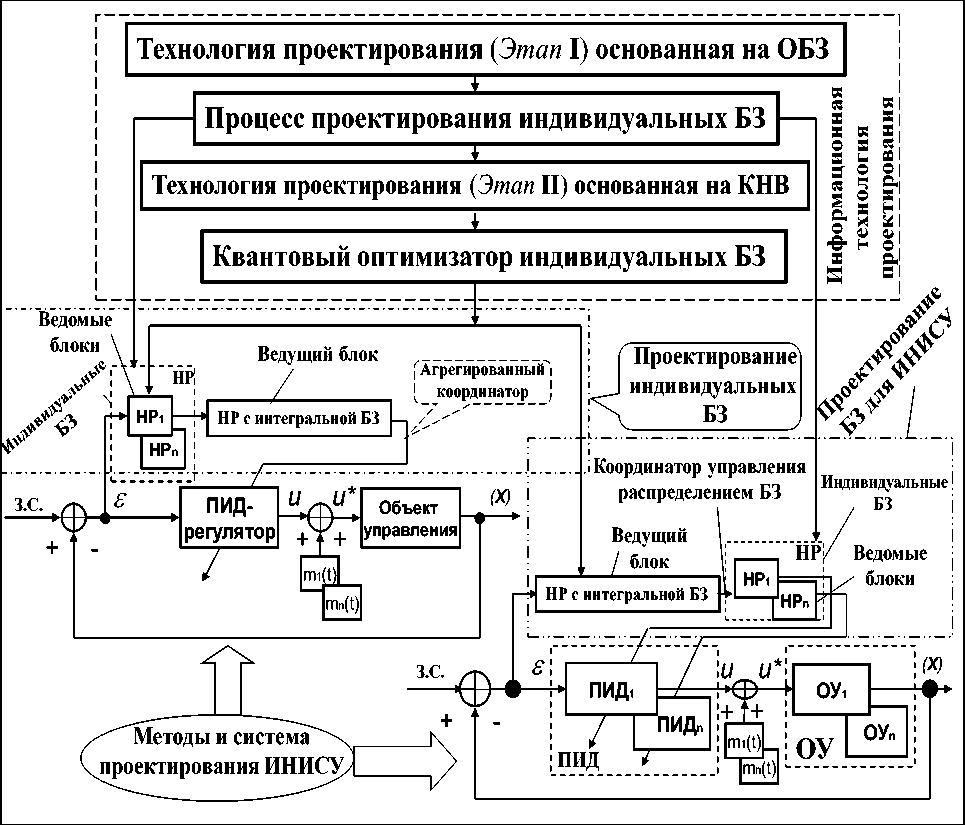
Рис. 5. Структура реализации ИСАУ, с соответствующими этапами

На первом этапе процесса проектирования формируются индивидуальные БЗ для двух (или более) нечетких регуляторов (НР), функционирующие в конкретных ситуациях управления. На данном этапе используются эволюционный многокритериальный генетический алгоритм с применением технологии мягких вычислений и нечеткого стохастического моделирования. Проведенные исследования показали существование достаточно широкой области сохранения робастности индивидуальных БЗ спроектированных на основе мягких вычислений. Использование этих технологий расширило область применения НР за счет добавления новых функций в виде обучения и адаптации.

Однако, при этом трудно спроектировать глобально «хорошую» и робастную структуру ИСУ. Данное ограничение особенно характерно для непредвиденных ситуаций управления, когда объект управления (ОУ) функционирует в резко изменяющихся условиях (отказ датчиков или шум в измерительной системе, наличие времени задержки сигналов управления или измерения, резкое изменение структуры ОУ или её параметров и т.п.). В ряде практических случаев такого рода условия могут быть предсказаны, но трудно реализовать робастное управление в непредвиденных ситуациях на основе спроектированной (для фиксированной ситуации управления) БЗ одного НР (даже на всем множестве) предсказанных случайных ситуаций.

Решение такого рода проблем может быть найдено на втором этапе проектирования на основе введения принципа самоорганизации в процесс функционирования БЗ для НР, который реализуется и программно поддерживается разработанной моделью квантового нечеткого вывода (КНВ) с применением методологий квантовых и мягких вычислений и системой инженерии - System of Systems Engineering , используя синергетический принцип самоорганизации.

В соответствии с законом информационного-термодинамического робастного интеллектуального управления (см. рис. 4), на этапе формирования БЗ интеллектуального регулятора (см. рис. 5), закладываются и реализуются устойчивые повторения режимов ускорения с минимальными затратами полезных ресурсов, таких как время настройки, потеря электроэнергии, износ оборудования и криогенные расходы.

Данные оптимальные режимы работы могут быть получены как на основе использования моделей ОУ и моделирования с привлечением вычислительных ресурсов суперкомпьютеров ЛИТ, на этапе проектирования и первоначальных запусков, так и на основе реального поведения ОУ в режиме on-line на GRID – технологиях, то есть из данных о состоянии системы с учетом заложенных особенностей её реализации.

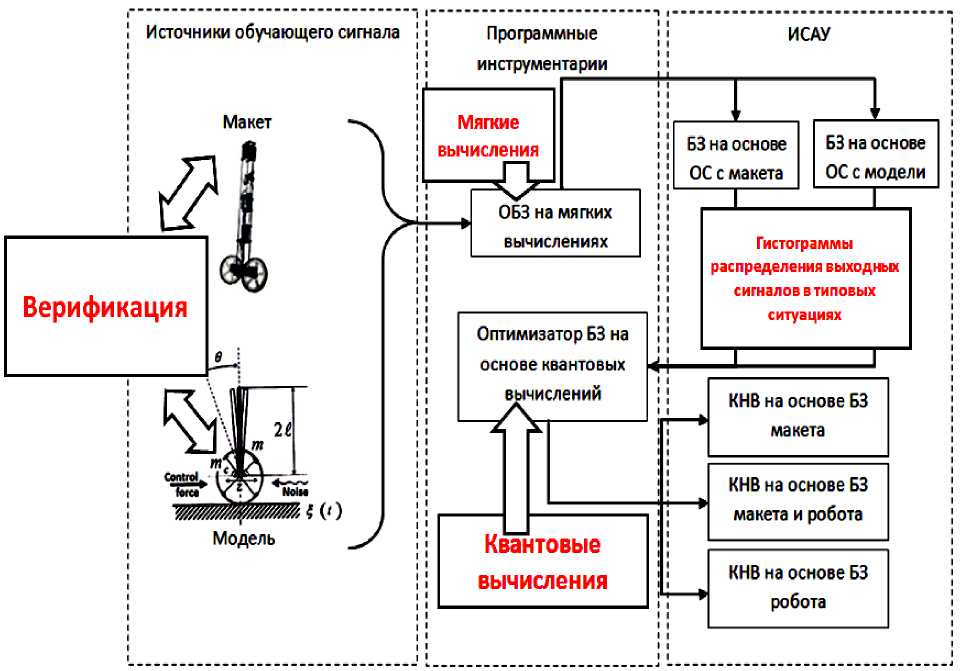
На рис. 6 представлена технология проектирования ИСУ, используемые при этом программные инструментарии на квантовых и мягких вычислениях, и возможные источники обучающих сигналов.

Макет

Control,

№1и

Модель

Источники обучающего сигнала

Оптимизатор БЗ на основе квантовых вычислений

Квантовые вычисления

ИСАУ

КНВ на основе БЗ макета

КНВ на основе БЗ макета и робота

КНВ на основе БЗ робота

Гистограммы распределения выходных сигналов в типовых ситуациях

Верификация в j

63 на основе БЗ на основе ОС с макета ОС с модели

Программные инструментарии

Мягкие вычисления

ОБЗ на мягких вычислениях

Рис. 6. Интеллектуальные системы управления и этапы проектирования

Одной из основных проблем эффективного применения технологии мягких вычислений в задачах управления являлось решение следующих задач:

• -    объективное определение вида функций принадлежности (ФП) и ее параметров в продукционных правилах в БЗ;

• -    определение оптимальной структуры нечетких нейронных сетей (ННС) в задачах глубокого машинного обучения (аппроксимация обучающего сигнала с требуемой (заданной) ошибкой и с минимальным количеством продукционных правил в БЗ);

• -    применение генетического алгоритма (ГА) в задачах многокритериального управления при наличии дискретных ограничений на параметры ОУ.

Перечисленные проблемы были решены и апробированы на основе представленного программного инструментария Оптимизатора Баз Знаний (ОБЗ) с применением технологии мягких вычислений [6, 28]. Разработанный интеллектуальный инструментарий позволил проектировать робастные БЗ на основе решения одной из алгоритмически трудно решаемых задач теории

Сетевое научное издание «Системный анализ в науке и образовании» Выпуск № 4, 2018 год искусственного интеллекта – извлечения, обработки и формирования объективных знаний без использования экспертных оценок.

В данном оптимизаторе используются три ГА, которые позволяют спроектировать оптимальную структуру нечеткого регулятора (вид и число ФП, их параметры, а также число самих правил нечеткого вывода), аппроксимирующей обучающий сигнал с требуемой ошибкой. При этом автоматически проектируется оптимальная структуры ННС и эквивалентного универсального аппроксиматора в виде нечеткого регулятора.

Объединение методологий стохастического и нечеткого моделирования ИСУ в инструментарии ОБЗ позволило повысить уровень робастности проектируемых БЗ и решать сложные задачи формирования объективных знаний [6, 7].

Входом ОБЗ является обучающий сигнал (ОС), который может быть получен либо на этапе стохастического моделирования поведения ОУ (с использованием его математической модели), либо экспериментально, т.е. непосредственно из результатов измерений динамических параметров физической модели ОУ, это позволяет учитывать заложенные неопределенности реального ОУ.

Инструментарий ОБЗ на мягких вычислениях

Структура ОБЗ и базовые шаги оптимизации представлены на рис. 7.

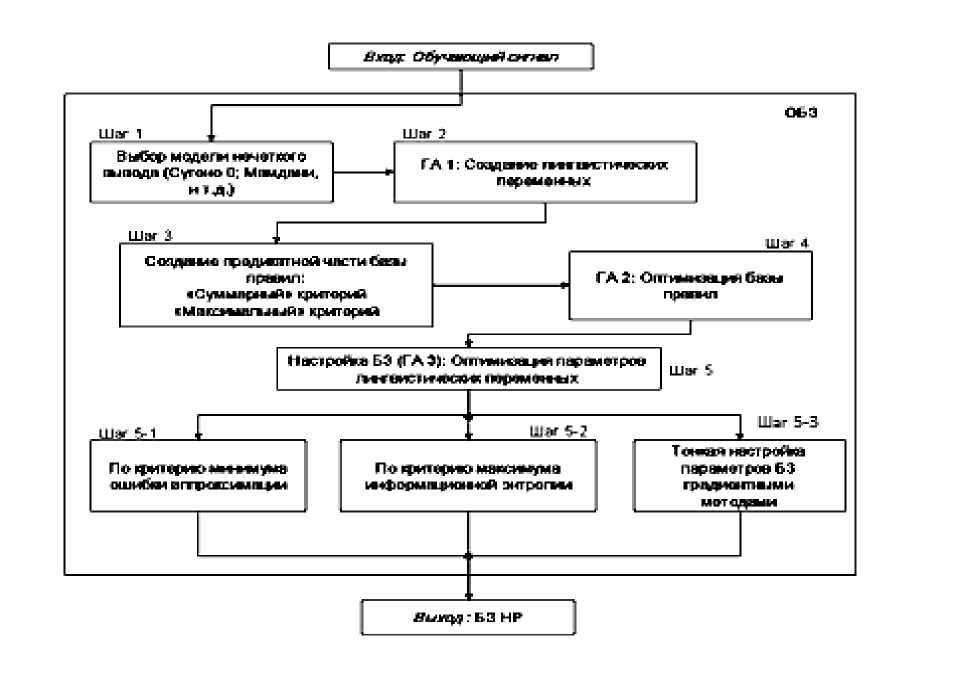
Рис. 7. Структура ОБЗ и шаги оптимизации БЗ

Структурно ОБЗ на мягких вычислениях состоит из взаимосвязанных генетических алгоритмов (ГА1, ГА2, ГА3), оптимизирующих отдельные компоненты БЗ и содержит следующие шаги алгоритма оптимизации:

Шаг 1: Выбор модели нечёткого вывода . Пользователь определяет тип нечёткой модели вывода (Сугено, Мамдани, и т.д.), и число входных и выходных переменных.

Шаг 2: Создание лингвистических переменных. С помощью ГА1 определяется оптимальное число функций принадлежности для каждой входной лингвистической переменной, а также выбирается оптимальная форма представления ее функций принадлежности (треугольная, Гауссовская и т.д.).

Шаг 3: Создание базы правил . На данном этапе используется специальный алгоритм отбора наиболее «робастных правил» в соответствии с заданными критериями

Шаг 4: Оптимизация базы правил . С помощью ГА 2 оптимизируются правые части правил БЗ. На данном этапе находится решение, близкое к глобальному оптимуму (минимум ошибки аппроксимации ОС). С помощью следующего шага 5 это решение может быть локально улучшено.

Шаг 5: Настройка базы правил . С помощью ГА3 оптимизируются левые и правые части правил БЗ, т.е. подбираются оптимальные параметры функций принадлежности входных/выходных переменных (с точки зрения заданной функции пригодности ГА). В данном процессе оптимизации используются различные функции пригодности, выбранные пользователем (шаги 5-1, 5-2 на рис. 7) . На данном этапе имеется также возможность настройки БЗ с помощью традиционного метода обратного распространения ошибки (см. шаг 5-3 на рис. 7).

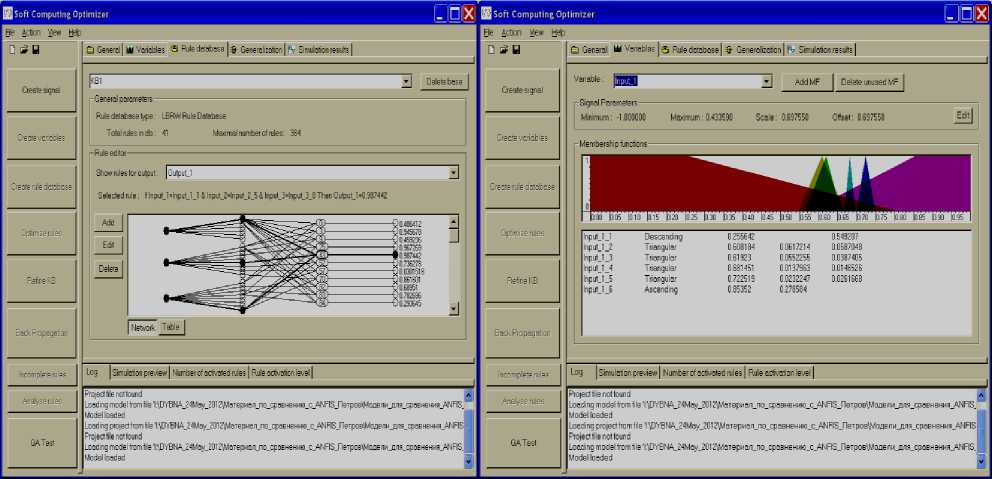
Результатом аппроксимации ОС является построенная БЗ нечеткого регулятора в виде нечеткой нейронной сети (рис. 8, а), включающая конечное множество правил и оптимально сформированные параметры функции принадлежности входных и выходных переменных НР (рис. 8, б), для заданной ситуации управления. Этап проектирования БЗ является первым этапом обобщенной технологии проектирования робастных ИСУ на основе квантовых и мягких вычислений (см. рис. 5). При этом данный этап позволяет работать как с реальным объектом управления, так и с его моделями; таким образом, реализуется принцип компенсации сложности и неполноты описания ОУ новыми видами интеллектуальных вычислений, которые закладываются при формировании базы знаний.

а

б

Рис. 8. Интерфейс оператора ОБЗ на мягких вычислениях. База знаний в виде нейронной сети (а), представление лингвистической переменной (б)

Рассмотрим кратко вопрос об эффективности разработанного интеллектуального инструментария ( Computational Intelligence Toolkit – CIT ).

Эффективность ОБЗ на мягких вычислениях для проектирования оптимальных структур нечетких нейронных сетей (ННС)

Разработанный интеллектуальный инструментарий позволил проектировать робастные БЗ на основе решения одной из алгоритмически трудно решаемых задач теории искусственного интеллекта – извлечения, обработки и формирования объективных знаний без использования экспертных оценок. Данная задача подробно была рассмотрена в [6], в которой приведены описание структуры ОБЗ, решаемые задачи оптимизации и дана постановка задачи. Согласно рис. 5, выходные данные из ОБЗ 18

на этапе I являются входными данными для этапа II, использующего КНВ для проектирования робастных БЗ. Поэтому отметим некоторые особенности ОБЗ на этапе I.

Как отмечалось выше, в разработанном оптимизаторе используются три ГА. Физически первый ГА осуществляет оптимизацию лингвистических переменных в левой части продукционного правила типа « Если А …», устраняет избыточность информации в обучаемом сигнале и реализует выбор оптимальной мощности терм-множеств лингвистических переменных компонент в обучаемом сигнале. Второй ГА осуществляет оптимизацию базы продукционных правил и реализует выбор оптимальных параметров правых частей продукционных правил типа «… ТО В» (рис. 9). Третий ГА осуществляет согласование правил и настройку БЗ. Применение данных ГА позволяет спроектировать, как следствие, оптимальную структуру ННС (вид функций принадлежности и их параметры, количество внутренних слоев и др.), аппроксимирующей ОС с требуемой ошибкой.

Рисунок 9 показывает результат применения второго ГА для оптимизации количества продукционных правил при аппроксимации сигнала обучения с заданной ошибкой аппроксимации, что существенно отличает разработанный метод проектирования от существующих, в которых ошибка аппроксимации не задается, а получается как результат аппроксимации. Таким образом, решается совместная задача проектирования оптимальной структуры ННС и глубокого машинного обучения7.

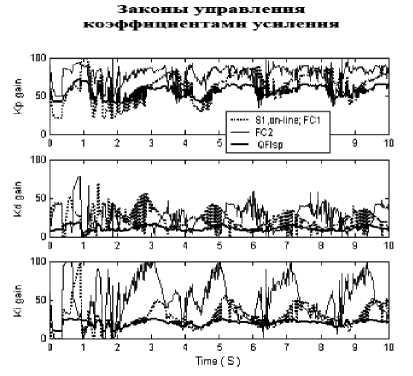
Рисунок 9 демонстрирует результат работы второго ГА в ОБЗ при проектировании законов управления коэффициентами усиления нечеткого ПИД-регулятора, используемых в примере моделирования системы «каретка перемещения – перевернутый маятник» (см. ниже).

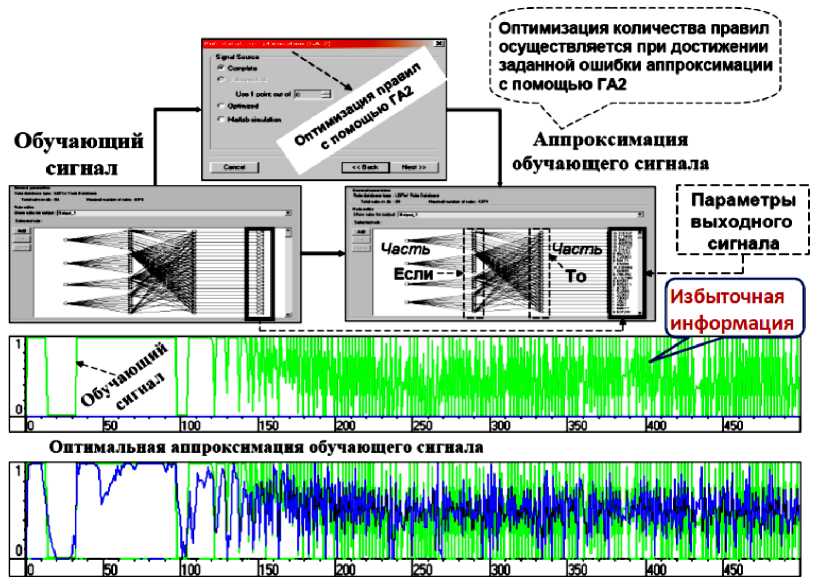
Рис. 9. Пример оптимизации количества продукционных правил при аппроксимации сигнала обучения с заданной ошибкой аппроксимации

Объединение методологий стохастического и нечеткого моделирования ИСУ в инструментарии ОБЗ позволило повысить робастность проектируемых БЗ и решать сложные задачи формирования объективных знаний.

Примечание. При существенном изменении среды функционирования или непредвиденных ситуациях управления, спроектированные законы управления, не всегда сохраняют свойство робастности. Данный эффект определяется функциональной структурой ГА, в которой (по определению) пространство поиска решений фиксировано и задается экспертом, а также выбором функции пригодности, которая рассматривается как критерий оптимальности управления. Мнение эксперта проявляется в общем случае в его опыте корректного задания пространства поиска ГА и знании вида функции пригодности. Таким образом, решение, найденное при помощи технологии мягких вычислений (на основе ГА) как оптимальное решение соответствует заданной ситуации управления, содержит (в неявном виде) субъективность исходной информации, а при неправильном определении пространства поиска и функции пригодности решение может неадекватно соответствовать заданной ситуации управления. Отметим, что решение задачи проектирования системы управления для нештатных ситуаций с помощью дополнительных корректирующих контуров управления восходит к середине 80-х годов прошлого столетия и приводит к появлению избыточности информации в контурах управления. Как следствие, это приводит к снижению надежности САУ.

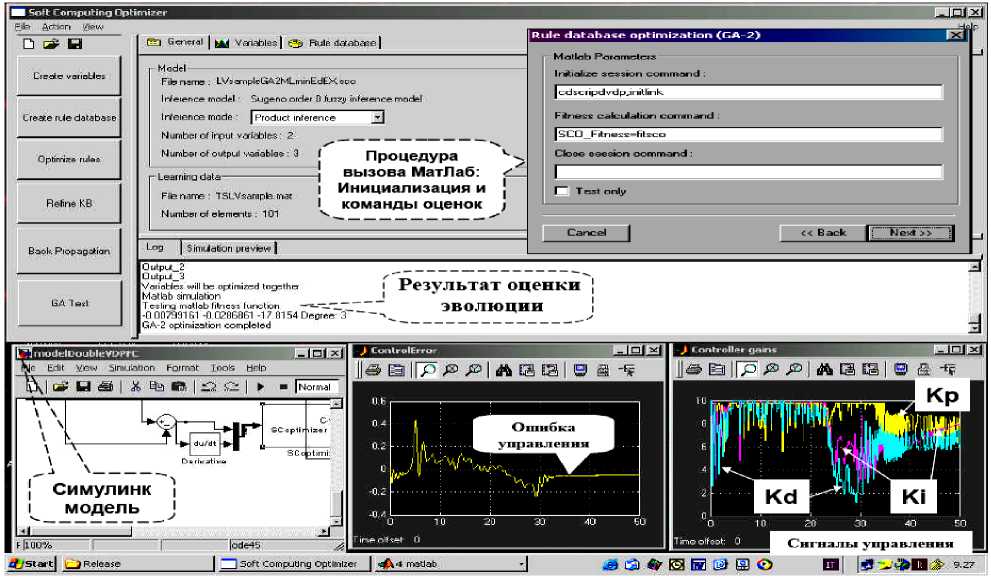
Рис. 10. Пример проектирования законов управления коэффициентами усиления нечеткого ПИД-регулятора с заданной ошибкой аппроксимации ОС

Отметим также, что современные ПИД-регуляторы все чаще на практике реализуются программным путем и на новой современной элементной базе (спинтроника). Поэтому обладают повышенной надежностью.

Инструментарий ОБЗ на технологии квантовых вычислений

Развитие ИТ проектирования ИСУ, основанное на применении технологии мягких вычислений, как показано выше, используют методологии нечеткой логики, эволюционных алгоритмов и нейронных сетей. Базисом развития систем управления послужили ПИД-регуляторы, которые зачастую, не справляются с задачей управления и плохо работают в непредвиденных ситуациях. Нечеткие регуляторы, позволяют частично расширить сферу применения ПИД регуляторов, за счет добавления правил функционирования и частично адаптировать систему. Использование генетических алгоритмов и нечёткой нейронной сети позволило полностью адаптировать систему, но для обучения такой системы требуются временные затраты, что в нештатных и непредвиденных ситуациях является критическим критерием. Моделирования оптимального сигнала позволяет создать частичную самоорганизацию в системе за счет обнаружения оптимальных траекторий коэффициентов усиления ПИД-регулятора. Применение квантовых вычислений и, как частного примера КНВ, позволяет повысить робастность без затрат временного ресурса в режиме реального времени.

На рис. 11 показана ИСУ с объединением нескольких нечётких регуляторов и КНВ, которая позволяет создать новое качество в управлении – самоорганизация в режиме online.

Как отмечалось, одна из главных проблем проектирования ИСУ заключается в том, что очень трудно спроектировать глобально хорошую и робастную структуру управления на все возможные случаи. Особенно, когда система работает в слабо предсказуемых ситуациях. Одно из лучших решений – формирование конечного числа баз знаний нечеткого регулятора для множества фиксированных ситуаций управления. Цель квантового регулятора объединить БЗ, полученные при помощи ОБЗ на мягких вычислениях, в самоорганизующиеся квантовые нечеткие регуляторы. КНВ использует частные индивидуальные БЗ нечеткого регулятора, каждая из которых получена с помощью инструментария ОБЗ на мягких вычислениях (см. рис. 5).

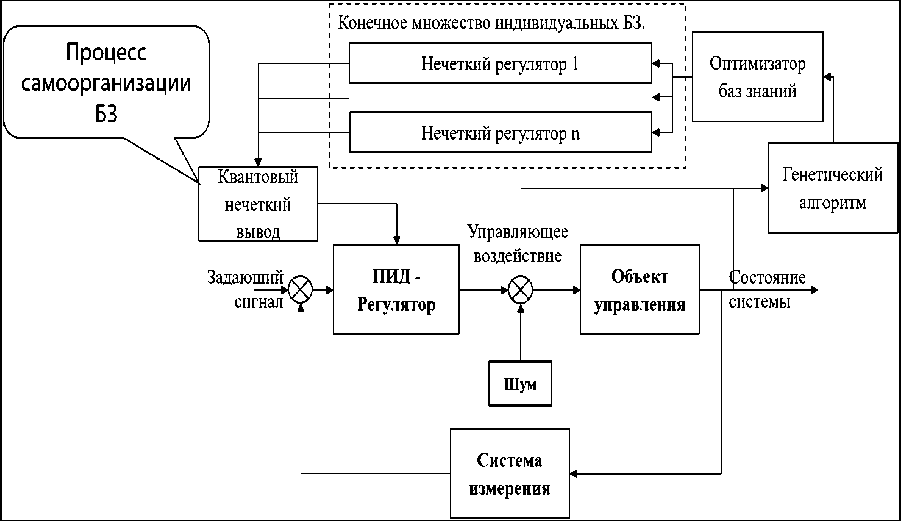
Рис. 11. Интеллектуальная система управления с квантовым нечетким выводом

Такой подход позволяет более полно и глубоко понять решение следующей трудной и принципиально важной для теории и систем управления проблемы (отмеченной ранее): определение роли и влияния квантовых эффектов на повышение уровня робастности проектируемых ИСУ . Эффективное применение квантовых эффектов в КНВ осуществляется за счет извлечения дополнительной квантовой информации, скрытой (и только частично доступной) в корреляционных классических состояниях законов управления, спроектированных только на основе классических методов технологии мягких вычислений. В результате срабатывает эффект редукции избыточной информации в классических законах управления коэффициентами усиления ПИД-регулятора.

Сам эффект редукции избыточной информации достигается за счет внедрения новых видов квантовой корреляции результатов реакций НР (с заданными БЗ) на непредвиденную ситуацию управления. Оптимальное соотношение типа и вида квантовой корреляции выполняет важную роль координированного управления коэффициентами усиления нечеткого ПИД-регулятора на нижнем исполнительском уровне ИСУ.

Квантовый нечёткий вывод с применением квантового генетического алгоритма

Процесс проектирования квантовой алгоритмической ячейки включает матричную форму трех квантовых операторов: суперпозиции, запутанности и интерференции, которые являются частью структуры квантовых поисковых алгоритмов. В общем виде структура квантовой алгоритмической ячейки (QAG) с применением квантового генетического алгоритма (QGA) описана в (1) в виде:

QAG = [ ( Int 0 ⁿ I ) • U_F ] h ^{+ 1} • [ QGA ] [ ⁿH 0 ^mS ] ,                    (1)

где I - тождественный матричный оператор; символ 0 обозначает тензорное произведение; S равен I или H (матрица Адамара) в зависимости от описания проблемы. Первая часть в проектировании уравнения (1) – это выбор типа оператора запутанного состояния U , который физически описывает качественные свойства функции.

Основным блоком такой интеллектуальной системы управления, является квантовый генетический поисковый алгоритм (КГПА, QGSA – quantum genetic search algorithm ) (см. рис. 12).

Основные элементы структуры квантового поискового алгоритма (КПА, QSA – quantum search algorithm ), как главного блока глобальной оптимизации, основанной на квантовых мягких вычислениях, представлены на рис. 13.

Формально структуру КГПА описывается следующим множеством логических операторов:

QGSA — { C,Ev,P >Ь,^П, X- цАсА-операторы'\.^^Р' En.t, 1п1^уд_оператОрЫ, Д }, где C – алфавит для генетического кодирования индивидуума для конкретной задачи; Ev- функция пригодности; P0 - начальная популяция; L - размер популяции; Q - оператор отбора (селекции); X - оператор скрещивания; ц - оператор мутации; Sup - квантовый оператор линейной суперпозиции; Ent - квантовый оператор запутывания (смешанное состояние); Inf – оператор вывода; А - условие остановки, включающие такие критерии остановки, как оптимум заданной функции пригодности и минимум энтропии Шеннона / фон Неймана.

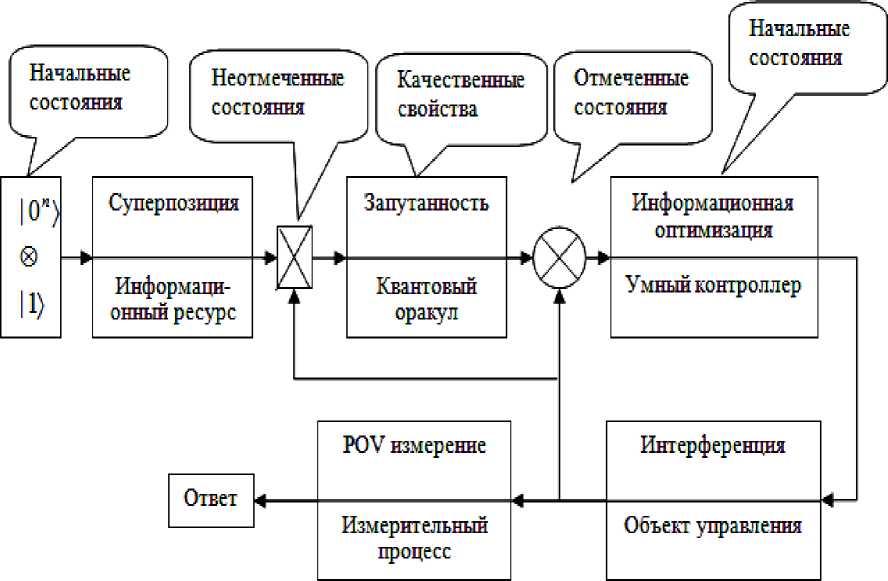
Рис. 12. Самоорганизующийся интеллектуальный квантовый поисковый алгоритм для интеллектуальной системы управления

Структура на рис. 12 – базовая модель интеллектуальной системы управления, описывает набор логических операторов КГПА. Комбинации логических операторов КГПА могут быть другими и отличатся от представленной формы, представляя различные варианты КПА8.

На рис. 13 представлена квантовая алгоритмическая ячейка ( QAG ) квантового нечеткого вывода. Такая ячейка может быть реализована как на классическом, так и на квантовом процессоре, а также может быть интегрирована в различные системы управления и встроенные интеллектуальные контроллеры. Алгоритм квантового нечеткого вывода для определения новых коэффициентов усиления ПИД-регулятора K (см. рис. 14), состоит из таких этапов, как нормализация, формирование квантового бита, после которого осуществляется подбор оптимальной структуры квантовой алгоритмической ячейки, выбирается состояние с максимальной амплитудой, осуществляется декодирование и на выходе получаем новый параметр коэффициентов усиления k традиционного регулятора.

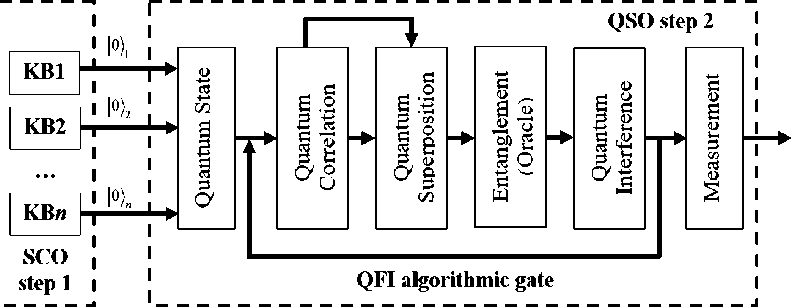
Рис. 13. Квантовая алгоритмическая ячейка (QAG) квантового нечеткого вывода

На входе КНВ получает коэффициенты от сформированных заранее баз знаний нечеткого регулятора [7] на основе оптимизатора БЗ на мягких вычислениях.

Примечание . Отметим, что разработанный квантовый генетический алгоритм и на его основе квантовый нечеткий вывод являются новыми квантовыми поисковыми алгоритмами.

Следующим шагов осуществляется нормализация полученных сигналов {0,1} путем деления текущих значений сигналов управления на их максимальные значения ( max k ), которые заранее известны.

Пример: Формирование квантовых битов . Определяются функции плотности распределения вероятностей. Они интегрируются и из них получаются функции распределения вероятностей. Они позволяют определить виртуальные состояния сигналов управления для формирования суперпозиции с помощью преобразования Адамара из текущего состояния введённых сигналов управления. Используется закон вероятности: p (| 0 ) ) + (|1 ) ) = 1 , где p (| 0 ) ) - вероятность текущего реального состояния, а p (| 1 ) ) - вероятность текущего виртуального состояния. По текущему реальному состоянию из закона сохранения вероятностей определяется виртуальное состояние.

Суперпозиция квантовой системы « реальное состояние – виртуальное состояние » имеет вид:

1 ^ ) = ^( V p (|0 ) )*|0 )+ 7 (1 - p (|0 ) ) *|1 ) ) .

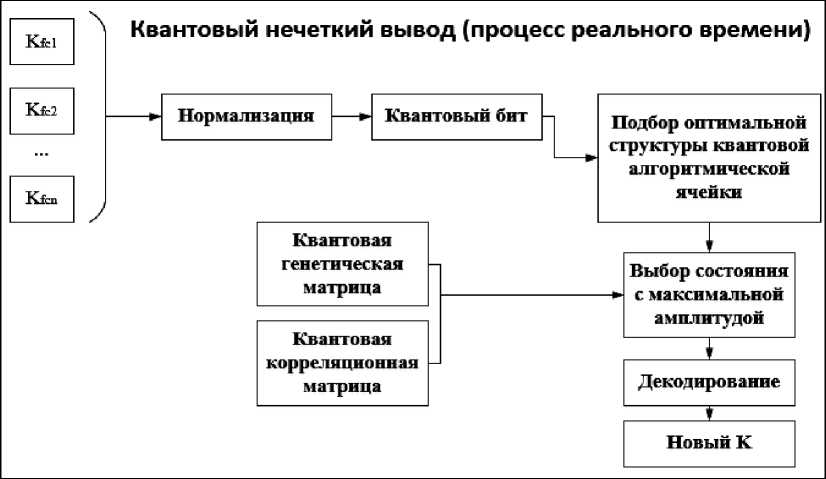
Рис. 14. Алгоритм квантового нечеткого вывода

На рис. 15 показан процесс формирования квантовых бит для текущего реального состояния нормированного сигнала управления, описывающего коэффициенты усиления нечеткого ПИД-регулятора.

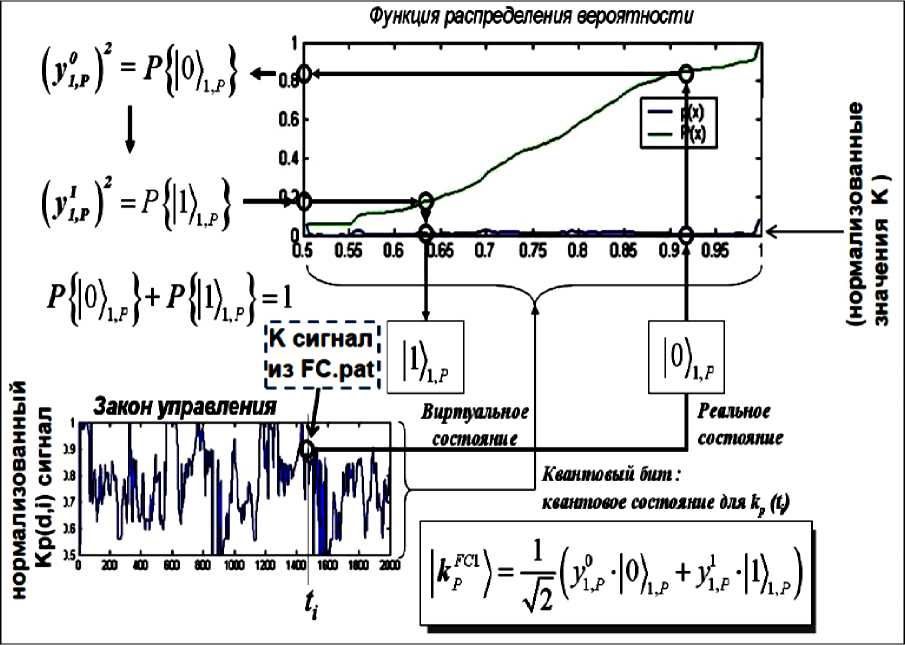
Рис. 15. Формирование суперпозиций состояний

На следующем этапе происходит выбор типа квантовой корреляции – операция построения запутанных состояний. Рассматривается 3 типа квантовой корреляции: пространственная, временная и пространственно-временная. Каждая из них содержит скрытую в спроектированных БЗ ценную квантовую информацию. Подробности работы квантового генетического алгоритма описаны в [7, 33].

В результате применения КНВ в структуре ИСУ осуществляется извлечение дополнительной (скрытой) квантовой информации, а ее использование дает возможность проектировать робастные сигналы управления в реальном времени из реакций НР на непредвиденные ситуации управления.

Примечание . Такой подход позволяет более полно и глубоко понять решение следующей трудной и принципиально важной для теории и систем управления проблемы (отмеченной ранее): определение роли и влияния квантовых эффектов на повышение уровня робастности проектируемых ИСУ . Эффективное применение квантовых эффектов в КНВ осуществляется за счет извлечения дополнительной квантовой информации, скрытой (и только частично доступной) в корреляционных классических состояниях законов управления, спроектированных только на основе классических методов технологии мягких вычислений. В результате срабатывает эффект редукции избыточной информации в классических законах управления коэффициентами усиления ПИД-регулятора.

Сам эффект редукции избыточной информации достигается за счет внедрения новых видов квантовой корреляции результатов реакций НР (с заданными БЗ) на непредвиденную ситуацию управления. Оптимальное соотношение типа и вида квантовой корреляции выполняет важную роль координированного управления коэффициентами усиления нечеткого ПИД-регулятора на нижнем исполнительском уровне ИСУ.

Рассмотрим пример эффективного применения КНВ в алгоритмически неразрешимой классическими подходами многокритериальной задачи оптимального управления в условиях неопределенности для объекта управления, представленного на рис. 16.

Пример: Квантовая декомпозиция многокритериального критерия в задаче глобальной оптимизации интеллектуального управления

Рассмотрим динамическую модель системы « движущаяся каретка – перевернутый маятник » (рис. 16, управляемой нечетким ПИД-регулятором по структурной схеме на рис. 5 (этап 1). Заданы следующие значения параметров: т_с = 1; m = 0.1; l = 0.5; k = 0.4; a_x = 0.1; a₂ = 5 и начального положения [ ^ ; ^ ; z ₀; z ₀] = [10;0.1;0;0] (величина угла отклонения маятника задана в градусах); ограничение на силу управления: - 5.0 <  и <  5.0 .

Особенностью задачи управления данным ОУ является использование одного нечеткого ПИД-регулятора для управления только перемещением каретки (с одной степенью свободы), в то время как сам ОУ имеет две степени свободы.

Целью управления является достижение углом отклонения маятника (второй обобщенной координаты) заданного положения через косвенное управление другой обобщенной координатой, используя соответствующие существенно нелинейные перекрестные связи с координатой перемещения каретки (эффект перекачки энергии между обобщенными координатами ).

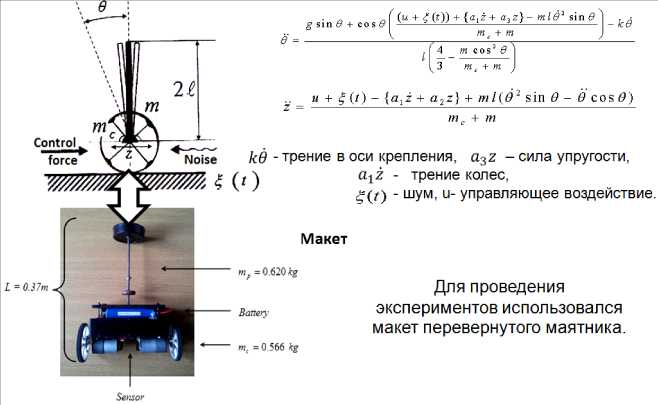
Рис. 16. Модель и макет системы каретка перевернутый маятник

Рисунок 17 иллюстрирует методологию тестирования робастности и источники непредвиденных ситуаций управления для ИСУ.

Сигнал поучения Ситуация-2

ситуации

I

I I

Выполняется после

Осреднение усиления

Оценка робастности регулятора моделирования КНР

Описание модели ОУ

Модель ОУ вкаретка-маятникв

Сигнал обучения Ситуация-1

Известные

Ситуация-2 р-Н*

Новая БЗ

на основе

КНВ

Коэффициенты шкалы (2.0, 0.6, 0.7}

Новая БЗ взвешенных

Без использования квантовых операторов

Ситуация-3

Непредсказуемые I смтуаымм

Процесс моделирования

Рис. 17. Тестирование робастности ИСУ в условиях непредвиденных ситуаций управления: схема и алгоритм тестирования

При одинаковых условиях обучения с помощью ОБЗ на мягких вычислениях БЗ1 нечеткого регулятора (НР 1 ) спроектирована по обобщенному критерию минимума среднеквадратичной ошибки:

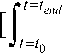
х ²

( t ) dt /|| х ||] + [f" '"х ²( t ) dt / х |]

t = '

а БЗ2 регулятора НР 2 спроектирована по обобщенному критерию минимума абсолютной ошибки положения маятника:

end | х ( т )| d x /1| х ||] + [ f end | х ( r )| d r /1 Х ||]

' = ' 0                                        ' = ' 0

Физически первый критерий (2) эквивалентен полной энергии перевернутого маятника, а второй критерий (3) характеризует абсолютную точность динамического поведения ОУ. Таким образом, первый критерий физический и эквивалентен полной энергии перевернутого маятника, а второй критерий относится к характеристикам качества управления и характеризует точность динамического поведения ОУ.

В качестве случайного сигнала для проектирования БЗ1 был выбран Гауссовский шум, а для формирования БЗ2 был выбран Рэлеевский шум.

На рис. 18 показаны БЗ1 и БЗ2 с соответствующими активизированными количеств правил 26 и 33 при общем количестве правил 729.

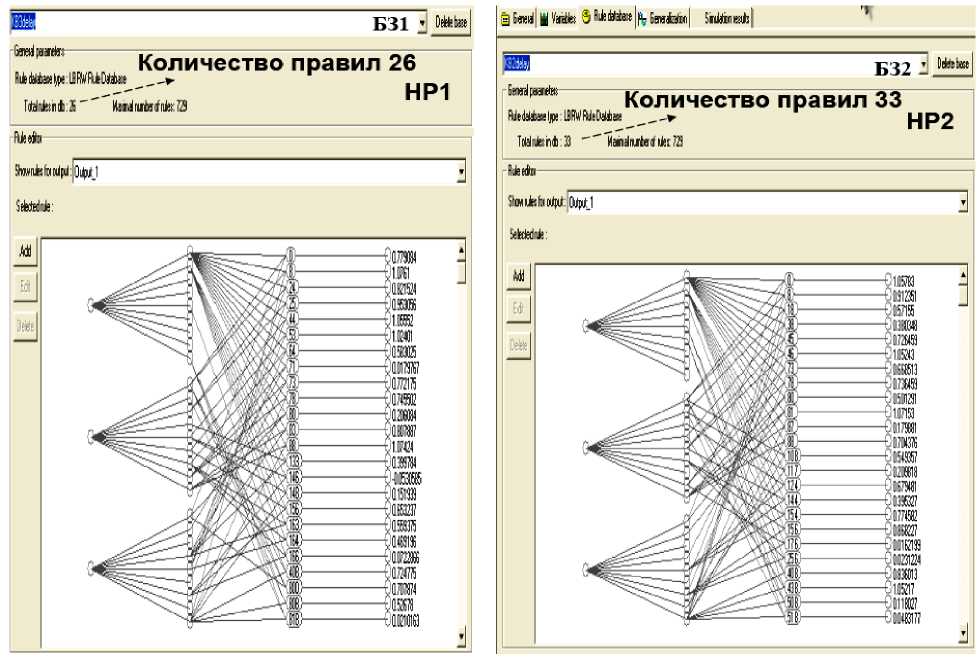
Рис. 18. Вид БЗ1 и БЗ2 с соответствующими активизированными продукционными правилами

По схеме на рис. 17,а были смоделированы две непредвиденные ситуации управления ( S 3 , S 4 ), в одной из которых ( S 3 ) был введен новый шум – случайный сигнал с равномерным одномерным распределением, задержка сигнала ошибки управления (0.003 сек), и сигнал шума в датчике измерения положения маятника (коэффициент усиления шума 0.015).

В ситуации ( S 4 ) был введен новый шум – случайный сигнал с гауссовским одномерным распределением, задержка сигнала ошибки управления (0.005 сек), и сигнал шума в датчике измерения положения маятника (коэффициент усиления шума 0.01).

На рис. 19 показан пример работы КНВ по формированию робастного сигнала управления пропорциональным коэффициентом усиления k в непредвиденной ситуации управления S 3 .

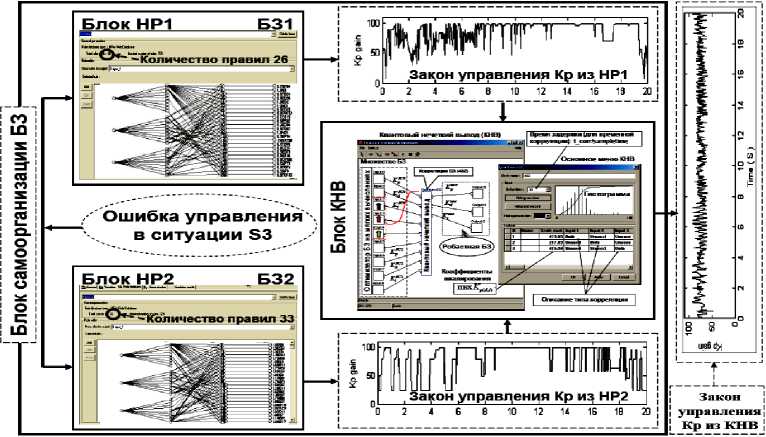
Рис. 19. Пример работы блока самоорганизации БЗ на основе КНВ

В этом случае выходные сигналы из БЗ1 и БЗ2 в виде реакции на новую ошибку управления в ситуации S3 поступают в блок КНВ. Выходом блока КНВ является новый сигнал управления коэффициентом k в реальном времени. Таким образом, блоки БЗ1, БЗ2 и КНВ на рис. 19 образуют блок самоорганизации БЗ в непредвиденной ситуации управления. Также на рис. 19 показаны законы управления самоорганизующегося квантового регулятора (КНВ), нечетких регуляторов НР1 и НР2.

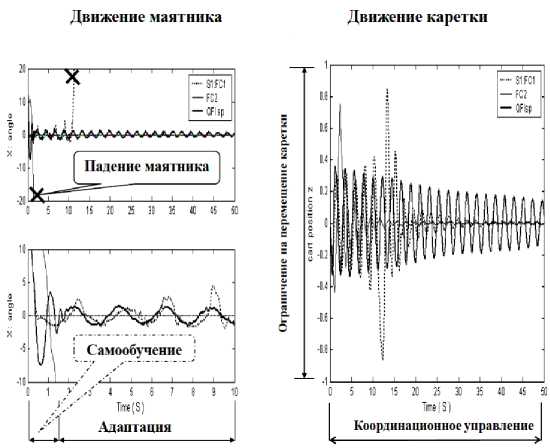
На рис. 20 показаны динамическое поведение исследуемой системы « движущаяся каретка – перевернутый маятник ».

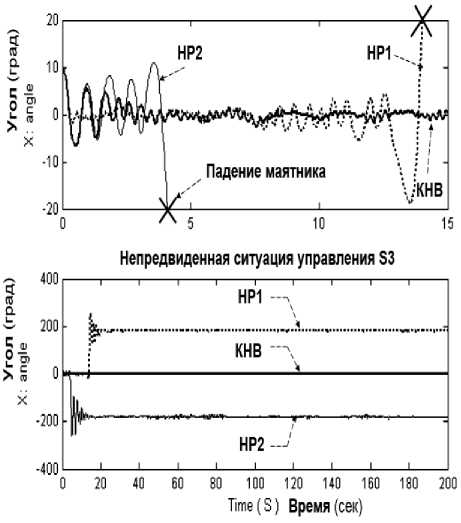
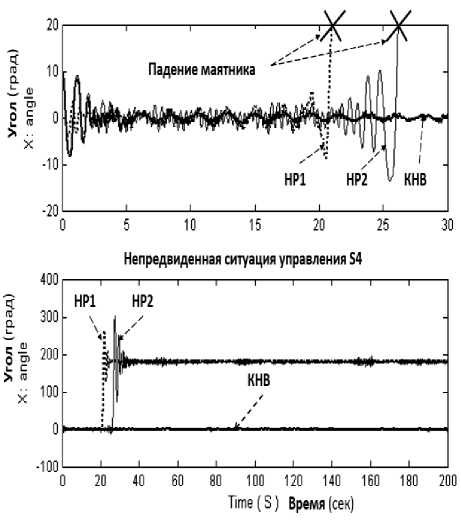
Рис. 20. Динамическое поведение перевернутого маятника в ситуациях управления (S3, S4)

Примечание . На рис. 20 и ниже приняты следующие обозначения: x = 6 - угол отклонения маятника от заданного положения, z – положение каретки, КНВ - квантовый НР с пространственной корреляцией. Для ряда непредвиденных ситуаций управления алгоритмы управления от ОБЗ на мягких вычислениях хорошо работают и держат маятник. На рис. 20 приведена сложная непредвиденная ситуация управления, когда другие законы управления не работают, но из них можно спроектировать робастный закон управления.

Результаты моделирования, представленные на рис. 20, показывают, что динамический ОУ в непредвиденных ситуациях управления ( S 3 , S 4 ) при управлении НР(1, 2) теряет устойчивость, а при управлении квантовым НР (КНВ) система управления обладает свойством робастности и достигается гарантированно цель управления.

На рис. 21 показаны интегральные динамические характеристики ОУ и точности управления.

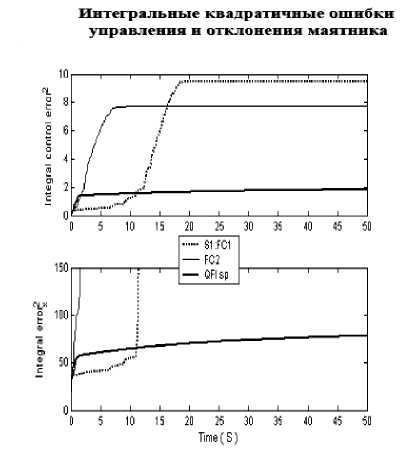
Результаты моделирования, представленные на рис. 21 показывают, что требуемое качество управления по приведенным критериям в непредвиденных ситуациях управления ( S 3 , S 4 ) при управлении НР(1, 2) также не достигается, в то время как при управлении кантовым НР (КНВ) система управления обладает требуемым качеством управления. Отсюда следует, что из двух не робастных НР с помощью квантовой самоорганизации знаний можно спроектировать в реальном времени робастный НР, БЗ которого удовлетворяет обоим критериям качества.

Результаты моделирования, представленные на рис. 20 и 21 показывают, что требуемое качество управления по приведенным критериям в непредвиденных ситуациях управления (S3, S4) при управлении НР1 и НР2 также не достигается, в то время как при управлении квантовым НР (КНВ) система управления обладает требуемым качеством управления. Отсюда следует, что из двух не робастных НР с помощью квантовой самоорганизации знаний можно спроектировать в реальном времени робастный НР, БЗ которого удовлетворяет обоим критериям качества.

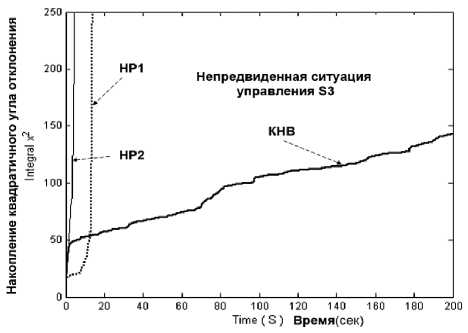
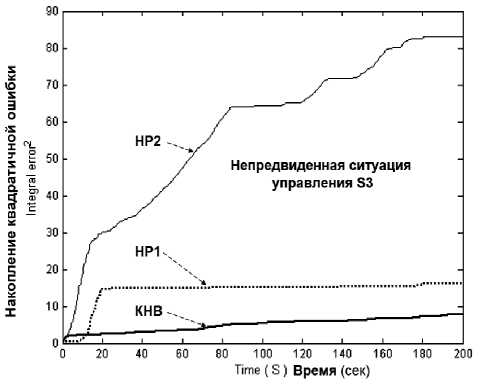
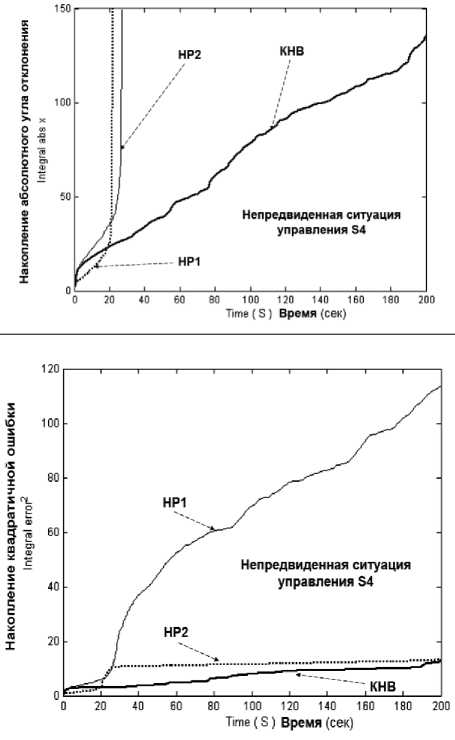
Рис. 21. Характеристики динамического поведения ОУ и точности управления

Следовательно, декомпозиция решения отмеченной выше задачи многокритериальной оптимизации робастной БЗ в непредвиденной ситуации управления на частные решения подзадач оптимизации физически может быть осуществлена в реальном времени в виде отдельных реакций соответствующих индивидуальных БЗ, оптимизированных с различными фиксированными критериями качества и ситуации управления. Агрегирование полученных частных решений в виде новой робастной БЗ осуществляется на основе КНВ, содержащего механизм суперпозиции между противоречивыми качествами управления и формирования квантовой корреляции между полученными частными решениями. В результате используются только реакции конечного числа индивидуальных БЗ, содержащие предельно достижимые законы управления в данной непредвиденной ситуации.

Формируемые новой робастной БЗ законы управления изменением коэффициентами усиления нечеткого ПИД-регулятора имеют более простую физическую реализацию и в результате содержат для непредвиденной ситуации управления лучшие характеристики индивидуальных критериев качества управления.

Таким образом, выходной сигнал КНВ представляет собой в режиме реального времени оптимальный сигнал управления изменением коэффициентов усиления нечеткого ПИД-регулятора, который включает в себя необходимые (наилучшие) качественные характеристики выходных сигналов управления каждого из НР с приоритетом и доминантной составляющей среди критериев качества управления, реализуя тем самым обобщенный принцип самоорганизации.

Такой подход открывает новые перспективы использования модели КНВ как частного варианта КА самоорганизации в задачах многокритериального управления ОУ со слабо формализованной структурой и большой размерностью фазового пространства управляемых параметров, использовать экспериментальные данные в виде обучающего сигнала без построения математической модели ОУ. Приведенные факты дают большое преимущество, которое выражается в виде возможности проектирования в реальном времени процессов управления с требуемой робастностью.

Следовательно, декомпозиция решения отмеченной выше задачи многокритериальной оптимизации робастной БЗ в непредвиденной ситуации управления на частные решения подзадач оптимизации физически может быть осуществлена в реальном времени в виде отдельных реакций соответствующих индивидуальных БЗ, оптимизированных с различными фиксированными критериями качества и ситуации управления.

Агрегирование полученных частных решений в виде новой робастной БЗ осуществляется на основе КНВ, содержащего механизм формирования квантовой корреляции между полученными частными решениями. В результате используются только реакции конечного числа индивидуальных БЗ, содержащие предельно достижимые законы управления в данной непредвиденной ситуации.

Формируемые новой робастной БЗ законы управления изменением коэффициентами усиления нечеткого ПИД-регулятора имеют более простую физическую реализацию и в результате содержат для непредвиденной ситуации управления лучшие характеристики индивидуальных критериев качества управления.

Следовательно, декомпозиция решения отмеченной выше задачи многокритериальной оптимизации робастной БЗ в непредвиденной ситуации управления на частные решения подзадач оптимизации физически может быть осуществлена в реальном времени в виде отдельных реакций соответствующих индивидуальных БЗ, оптимизированных с различными фиксированными критериями качества и ситуации управления.

Формируемые новой робастной БЗ законы управления изменением коэффициентами усиления нечеткого ПИД-регулятора имеют более простую физическую реализацию и в результате содержат для непредвиденной ситуации управления лучшие характеристики индивидуальных критериев качества управления (см. рис. 19).

Пример : Робастность ИСУ в непредвиденных ситуациях управления . Рассмотрим теперь задачу оценки робастности ИСУ динамическим ОУ в условиях непредвиденных ситуаций управления.

Рисунок 17 показывает классификацию непредвиденных ситуаций управления для ОУ, сочетание которых составляет практически необозримое количество нештатных ситуаций. Достижение робастности ИСУ является сложной и важной задачей.

На рис. 22 показаны эффективные результаты моделирования ИСУ на непредвиденную (физически неоднородную) ситуацию управления: в схеме новое время задержки сигнала датчика = 0.002 сек; внутренний Гауссовский шум с амплитудой = 0.01; новые начальные условия [ 0 , . 0 > ] = [ 13,1 ] ( в гр. ) , [ z „ , z . ] = [ 0,0 ] . Внешний Рэлеевский шум выбран в ситуации обучения. Примечание . На рис. 22 и ниже приняты следующие обозначения: x = 0 - угол отклонения маятника от заданного положения, QFIsp - квантовый НР с пространственной корреляцией.

На рис. 23,а показаны эффективные результаты моделирования ИСУ на более сложную непредвиденную (также физически неоднородную) ситуацию управления.

Введено новое время задержки сигнала датчика = 0.003 сек; внутренний Гауссовский шум с амплитудой = 0.02; случайные параметры модели k , a_x , си определялись в виде:

k s = k + gain_k ^ ( t ) = 0.4 + 1 • ^ ( t ); a_x = a_x + gain_at ^ ( t ) = 0.1 + 0.5 • ^ ( t );

a s = a ₂ + gain_a ^(t ) = 5 + 2 • ^ ( t ), где £ ( t ) - Гауссовский белый шум с единичной амплитудой;

новые начальные условия: Г 0 , 0 1 = [ 13,1 ] ( в ^гр.) , [ ^z 0 , ^z 0 ] = [ ^0,0 ] .

(а)

(в)

(б)

(г)

Рис. 22. Результаты моделирования ИСУ на непредвиденную (физически неоднородную) ситуацию управления

Особенностью данной ситуации является внешний шум, моделирующий шероховатость поверхности передвижения каретки с установленным маятником и имел переменную функцию плотности распределения вероятностей, и показан на рис. 23,б (сочетание непредвиденных ситуаций [1 + 2 + 3] на рис. 17).

Из результатов моделирования, представленных на рис. 22 и 23 следует неожиданный (для классической логики проектирования ИСУ) результат: из двух не робастных НР-1,2 с помощью КНВ в реальном времени может быть спроектирован робастный квантовый НР. Отметим, что использовалась оптимальная квантовая пространственная корреляция между двумя сигналами управления из БЗ нечетких ПИД-регуляторов.

Приведенный эффект имеет чисто квантовую природу и у него нет классического аналога.

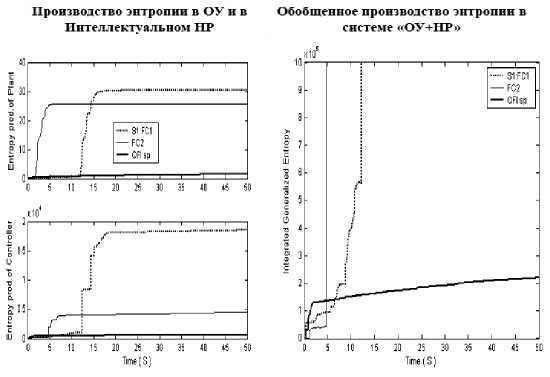
Из результатов моделирования (рис. 22(в)) следует также, что обобщенное производство энтропии в системе «ОУ + нечеткий ПИД-регулятор» является минимальным и в процессе квантовой самоорганизации в структуре ИСУ достигается требуемый термодинамический критерий оптимального распределения между устойчивостью, управляемостью и робастностью (рис. 4). Модели систем управления на основе скользящих режимов с использованием ГА и других методов технологии мягких вычислений, оптимизации нечетких ПИД-регуляторов на основе эволюционного программирования, дифференциальной эволюции, swarm computational intelligence и т.п. в условиях непредвиденных ситуаций управления не обладают глобальной робастностью и/или имеют дополнительно более сложную структуру регулятора.

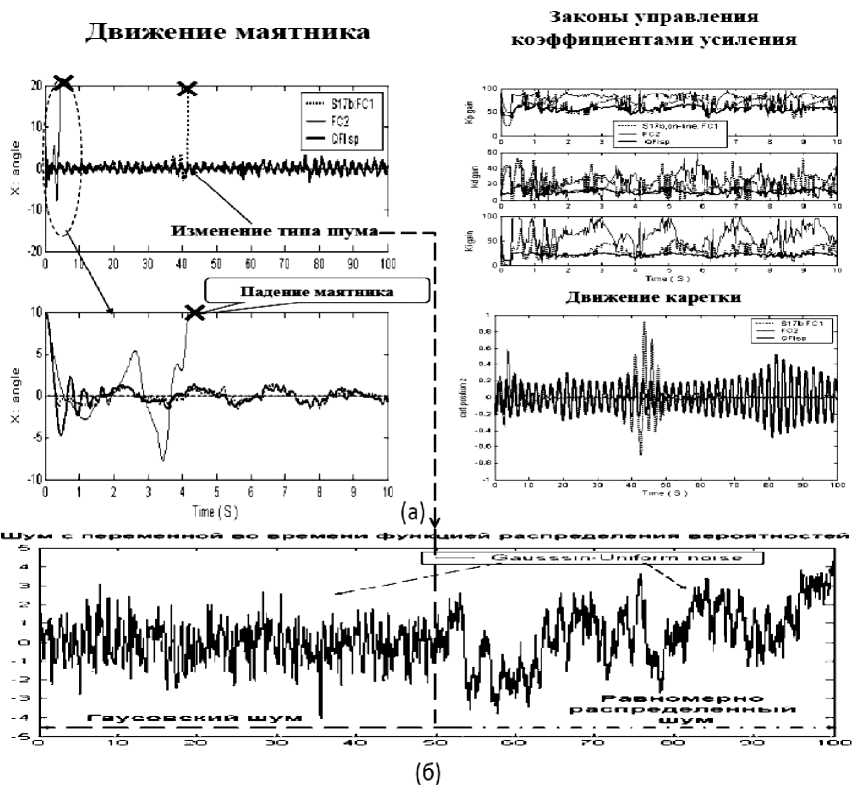
Рис. 23. Робастность ИСУ на непредвиденную ситуацию управления

Пример : Применение ОБЗ на квантовых вычислениях с обучающим физическим сигналом с ОУ . На рис. 24 представлены результаты проведенного математического моделирования и физического эксперимента регистрации обучающего сигнала в нештатной ситуации управления.

В качестве нештатной ситуации выбрана ситуация с увеличением задержки сигнала обратной связи в три раза.

Исследование подтвердило существование синергетического эффекта самоорганизации в процессе формирования робастной БЗ из спроектированных не робастных БЗ. При этом дополнительный информационный ресурс для управления основан на извлечении скрытой в классических состояниях квантовой информации. Метод проектирования ИСУ позволил достигать глобальной робастности в режиме реального времени за счет использования новых типов вычислений, таких как квантовые и мягкие вычисления, при этом использовались вычислительные ресурсы классического процессора.

Таким образом, данный инструментарий реализует принцип самоорганизации БЗ на основе квантового подхода и осуществляет оптимизацию термодинамического критерия распределения качества управления как устойчивость, управляемость и робастность.

Поэтому разработанный квантовый алгоритм является новым квантовым поисковым алгоритмом.

Решение задачи проектирования робастного управления классическим ОУ (глобально неустойчивым и существенно нелинейным) рассматривается в качестве примера ( Benchmark ) эффективного использования разработанной информационной технологии проектирования ИСУ.

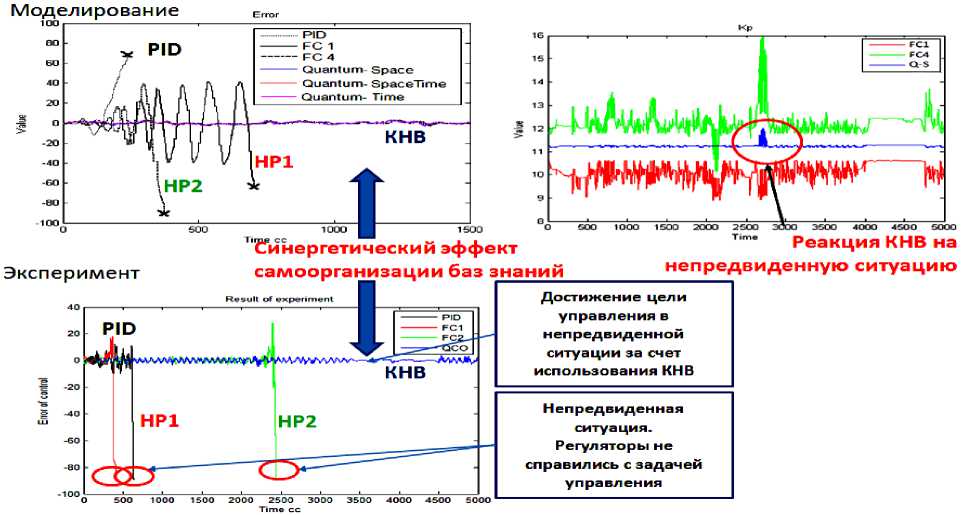
Рис. 24. Результаты моделирования и эксперимента, проведенного в непредвиденной ситуации управления для классического ПИД регулятора, нечеткого регулятором и регулятора на КНВ

Данный пример иллюстрирует возможность эффективного применения технологии квантовых вычислений для решения таких алгоритмически неразрешимых задач классическими методами как проектирование глобальной робастности ИСУ в условиях непредвиденных ситуаций управления. Положительные результаты применения классических технологий интеллектуальных вычислений (типа мягких вычислений) совместно с аппаратом квантовых вычислений привело к новому альтернативному подходу – применению технологии квантовых интеллектуальных вычислений в задачах оптимизации процессов управления классическими ОУ (физический аналог применения обратного метода исследования « квантовая система управления – классический ОУ »), что существенно расширяет возможности самих интеллектуальных вычислений.

Преимущества и возможности использования робастной самоорганизующейся ИСУ описаны также в [6, 7]. Обобщение полученных соотношений на более широкий класс динамических систем (порт-управляемые Гамильтоновы системы – port-controlled Hamiltonian systems ) приведено в [30].

Примечание. В данной статье не рассмотрены такие важные проблемы как: 1) оценка необходимого числа ситуаций обучения для проектирования индивидуальных БЗ, гарантирующих достижение глобальной робастности НР в непредвиденных ситуациях управления; 2) оценка качества управления по суммарным критериям включающих в себя критерии минимума производства энтропии, минимума среднеквадратичной ошибки управления, простоты законов управления и др.; 3) робастное управление существенно-нелинейными ОУ с локальной и глобальной неустойчивостью по части обобщенных координат; 4) разработка и оценка точности субоптимальных робастных БЗ для НР в ИСУ для слабо структурированных моделей ОУ; 5) программно-аппаратная поддержка интеллектуальных вычислений и робастных ИСУ и мн. др.

Комментарий. Положительный эффект повышения уровня робастности достигается, в частности, за счет метода извлечения дополнительной квантовой информации, скрытой (и только частично доступной) в корреляционных классических состояниях законов управления, и спроектированных только на основе классических методов технологии мягких вычислений. В настоящей работе приведено описание разработки данного метода для применения в решении проблемы формирования робастных БЗ на основе квантовых стратегий принятия решений в игровых ситуациях и неопределенности ситуаций управления.

Приведенные результаты позволяют более полно и глубже понять решение следующей трудной и принципиально важной для теории и систем управления проблемы: определение роли и влияния квантовых синергетических эффектов на повышение уровня робастности проектируемых интеллектуальных процессов управления.

• 1.    В данной работе решение поставленной проблемы основано на выявлении возможности извлечения дополнительной квантовой информации, скрытой (и только частично доступной) в корреляционных классических состояниях законов управления, и спроектированных только на основе классических методов технологии мягких вычислений.

• 2.    Разработанная модель квантового нечеткого вывода с применением в своей структуре квантового генетического алгоритма в квантовой суперпозиции для выбора типа и вида корреляции реализует принцип самоорганизации БЗ в непредвиденных ситуациях управления и оптимального распределения уровней устойчивости, управляемости и робастности в соответствии с разработанным термодинамическим критерием качества управления (принцип минимума обобщенного производства энтропии и требуемой исходной информации о среде функционирования ОУ).

• 3.    При этом проявляется эффект редукции избыточной информации в классических законах управления коэффициентами усиления ПИД-регулятора за счет использования квантовых эффектов.

• 4.    Данный эффект достигается за счет использования новой ценной квантовой информации, извлеченной в реальном времени из результатов реакций классических НР (с заданными БЗ) на непредвиденную ситуацию управления, с помощью новых видов квантовой корреляции.

• 5.    Созданные квантовым процессом проектирования робастные БЗ формируют законы управления в реальном времени с минимальной алгоритмической сложностью их физической реализации и с минимальными потерями полезного ресурса (минимум производства обобщенной энтропии в системе «ОУ + самоорганизующийся интеллектуальный регулятор») для различных (физически неоднородных) классов непредвиденных ситуаций управления.

• 6.    Полученные результаты позволяют продемонстрировать эффективность квантового алгоритма управления самоорганизацией робастных БЗ в условиях непредвиденных ситуаций управления как нового направления в теории и систем управления плохо формализованными моделями ОУ.

• 7.    Разработанная программная поддержка реализации квантовых вычислений на классических персональных компьютерах и ГРИД-технологиях открывает новые возможности инженерной практики эффективного применения технологии квантовых мягких вычислений в проектировании ИСУ.

Результаты моделирования, представленные на рис. 22 показывают, что требуемое качество управления по приведенным критериям в непредвиденных ситуациях управления при управлении НР1 и НР2 также не достигается, в то время как при управлении квантовым НР (КНВ) система управления обладает требуемым качеством управления. Отсюда следует, что из двух не робастных НР с помощью квантовой самоорганизации знаний можно спроектировать в реальном времени робастный НР, БЗ которого удовлетворяет обоим критериям качества заложенным при проектировании НР на первом этапе технологии.

Важное преимущество технологии заключается в следующем, на этапе проектирования БЗ в качестве источников обучающего сигнала можно использовать как различные модели ОУ, так и физические сигналы о его реальном состоянии.

Так в представленных результата (рис. 24) в качестве таких источников для НР1 выступала математическая модель системы, а НР2 был спроектирован на основе сигнала полученного непосредственно с объекта управления. При этом, использование сигнала с реального объекта, позволяет учитывать заложенные в него неопределенности, люфты, шумы в системе измерения и управления. Данное обстоятельство позволило включать особенности объекта управления не доступные в работе с моделью при извлечении объективных знаний для формировании управляющих воздействий в КНВ.

Возможные применения технологий интеллектуальных вычислений и управления в мегапроекте NICA

В качестве цели применения интеллектуальных технологий управления в NICA можно рассмотреть решение следующих задач:

• -    повторяемость требуемых режимов ускоряемых пучков ядер с предварительно заданными параметрами;

• -    автоматическое управление функционированием коллайдера NICA за счет добавления свойств адаптации, обучения и самоорганизации в подсистемы управления с целью обеспечения устойчивости и повторяемости режимов ускорения и минимизации издержек эксплуатации системы;

• -    обеспечение устойчивой динамики пучков на всех этапах цикла;

• -    снижение издержек;

• -    управление подсистемами в непредвиденных и нештатных ситуациях.

Использование регуляторов на основе представленной технологии проектирования рекомендуется для повышения надежности при управлении автономными, сложными, слабо формализованными и слабо структурированными объектами управления, функционирующих в нештатных и непредвиденных ситуациях управления.

О возможном решении задачи обеспечения устойчивой динамики пучков

Процессы разработки и реализации элементов ускорительной техники, и системы управления неразрывно связан. В частности, исследователи и операторы, руководствуюсь моделями процессов ускорения и динамики пучков, оптимизируют работу системы управления. Данные экспериментов используются для обновления, верификаций и валидации этих автономных моделей и обеспечения более точного предсказания набора оптимальных настроек. В инструментарии исследователей-инженеров существует множество программных решений, основанных на моделях частиц и событий. К таким программам относятся ZGOUBI , MAD и MAD-X , PTC , PARMILA , Trace 3 D , применяются модели реакции глубокого расщепления – CEM , Phits , Cascade , модели адиабатического захвата – ESMS и мн. др. [49-52].

Суть применения ИСУ может заключаться в автоматическом получении набора рекомендованных параметров и синхронизации работы последовательности систем ускорительного комплекса. Например, в эксперименте по «ручной» экспериментальной настройке оптимального режима в 45-м сеансе Нуклотрона пучок инжектировался на «стол» магнитного поля, соответствующего энергии инжекции, за 100–150 мс до начала его роста [21]. Переход со «стола» поля инжекции к его постоянному росту со скоростью 0,3 Тл/c осуществлялся по параболе в течение 100 мс. Закон изменения амплитуды ВЧ–напряжения предварительно определялся численным моделированием динамики частиц, а в ходе настройки оптимизировался на основе анализа процесса формирования сгустков.

На рис. 25 приведена зависимость интенсивности пучка от времени в случае, когда амплитуда ВЧ – напряжения на «столе» поля менялось параболически с 500 В до 3 кВ.

Переход к ускорению (на параболическом участке роста поля) сопровождался линейным ростом амплитуды ВЧ – напряжения с 3 до 6 – 7 кВ. При этих параметрах удалось обеспечить устойчивый процесс формирования сгустков и переход к ускорению с минимальными потерями интенсивности (Рис. 25).

В процессе перестройки частоты ВЧ станций появляются непредвиденные «паразитные» колебания, частотный спектр которых невозможно предсказать. В таких условиях задача разработки самоорганизующихся ИСУ, способных функционировать и гарантировать достижение цели управления в условиях нештатных ситуаций и информационного риска, является актуальной для комплекса NICA .

Закон изменения магнитного поля B 0 (t) в синхротронах задаётся управляемыми сильноточными источниками системы питания магнитов и зависит от параметров системы питания и требованиями эксперимента. Например, функция B 0 (t) близка к трапециевидной форме (Рис. 25) с экспоненциальными переходами между плато («столом») и линейным ростом B 0 (t).

Рис. 25. Временные зависимости магнитного поля (кривая 1), амплитуды напряжения ускоряющего ВЧ–поля (кривая 2) и интенсивности пучка (кривая 3) в процессе АЗ. Цена деления по шкале времени 300 мс (45-й сеанс Нуклотрона)

В зависимости от величины и формы ведущего магнитного поля ускорителя ИСУ способна настраивать частоту (f) и амплитуду (A) ускоряющей частоты так, чтобы получить заданную интенсивность (J) пучка частиц в конце цикла ускорения на «столе» магнитного поля (Рис. 26).

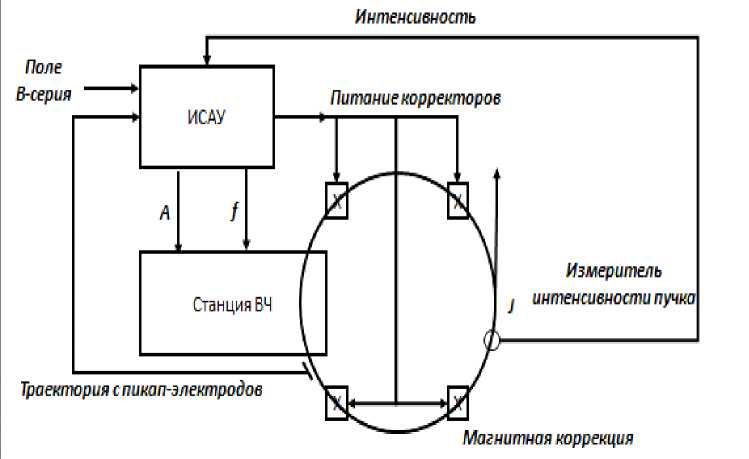
Рис. 26. Упрощенный вариант структуры системы управления с обратной связью.

(Ядром ИСУ является интегрированная база знаний)

Характеристики цикла задает именно закон изменения магнитного поля, при этом математическая детерминированная модель зависимости частоты ускоряющего напряжения f от ведущего магнитного поля B о с релятивистской поправкой имеет вид [53]:

f= т/2п, где to

MqB_Q / m₀

V i + ( qB о RI m о c ^{) 2}

Здесь M - кратность частоты ускорения (количество банчей в кольце), q и т о - заряд и масса покоя ускоряемого иона, R - эффективный радиус траектории пучка в ускорителе (для Нуклотрона R = 22,002 м), c = 2.998x10 8 т / 5 - скорость света.

Решение этой задачи связано с необходимостью реализации ряда новых физических и информационно-термодинамических принципов:

• -    принцип компенсации информационной неполноты модели ускорителя;

• -    принцип соответствия алгоритма интеллектуального управления уровню сложности и неполноты представления знаний о внешней среде функционирования;

• -    принцип минимума потерь полезного ресурса;

• -    принцип иерархического построения ИСУ так, что верхний надстраиваемый уровень не разрушает, а повышает эффективность нижнего исполнительского уровня системы управления за счет самоорганизации базы знаний интеллектуального регулятора.

Рекомендация на выбор типа интеллектуального управления

Из многочисленных моделей управления предлагается использовать технологии мягких и квантовых вычислений, т.к. эти инновационные сквозные квантовые технологии составляют программно–алгоритмическую платформу для проектирования самоорганизующихся ИСУ, способных функционировать и гарантировать достижение цели управления в условиях непредвиденных (нештатных) ситуаций и информационного риска с требуемым уровнем робастности (Рис. 27).

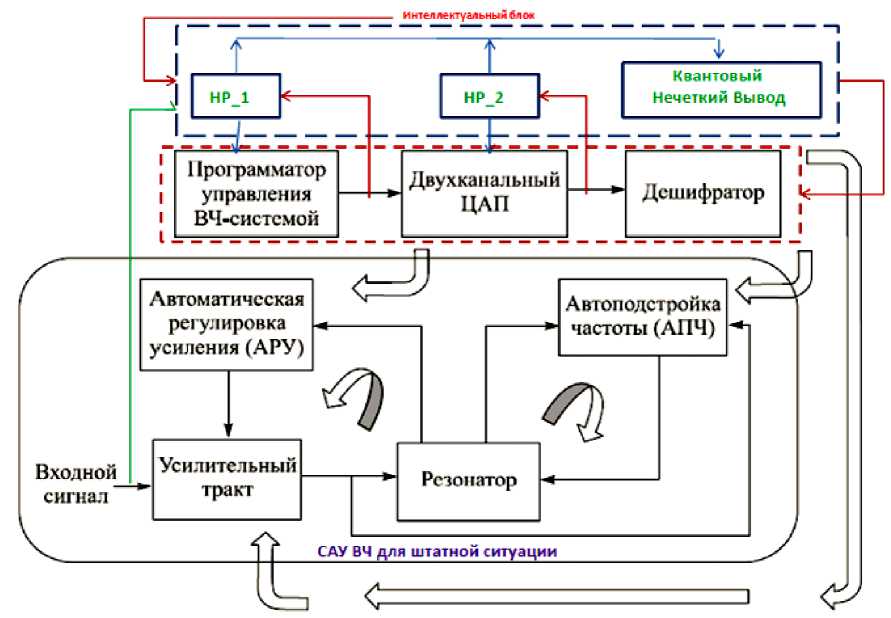
Рис. 27. Интеллектуальная надстройка в виде НР и КНВ в задаче управления ВЧ

На рис. 27 представлена двухуровневая система управления, где на нижнем уровне осуществляется сбор, обработка и хранение информации для формирования управляющего воздействия на исполнительные устройства. На верхнем уровне, формирующем воздействия на исполнительные механизмы ускорителя NICA, представление и передача знаний, и обратные связи передачи информации, реализующие управляющие контуры для поддержания режима функционирования системы в автоматическом режиме. Формирования такой системы позволит повысить эффективность работы NICA, понизить потери полезного ресурса регуляторов и требует минимальной исходной информации для выработки управляющих воздействий. Разработка и внедрение иерархической ИСУ позволит решить задачи гарантированного достижения цели управления и соответственно ожидаемого результата в режиме работы ускорителя.

Программно-алгоритмическая поддержка и инструментарий интеллектуально го управления на основе ГРИД технологии и суперкомпьютинга

В задаче получения, хранения и анализа больших экспериментальных данных физических установок принято использовать технологии распределённых вычислений (ГРИД-технологии). Обрабатываемые результаты могут быть использованы для выявления ошибок управления и коррекции управляющих воздействий, при этом верификация моделей и идентификация ОУ требует затрат больших вычислительных ресурсов и соответственно применения технологий суперкомпьютинга. Однако, с одной стороны связанная с физической сложностью и неполнотой описания модель, не является физически строгой и математически корректной (с нечеткой границей ее строгости и корректности). С другой стороны необходимо учитывать физические особенности установки, режимы ее функционирования, влияния окружающей среды и мн. др. факторы.

Решение проблемы проектирования робастной ИСУ в перечисленных условиях функционирования и ограничениях может быть найдено за счет применения разработанной сквозной квантовой технологии.

Верифицированные модели и реальные измеряемые физические сигналы поведения ОУ являются информационными источниками для получения обучающих сигналов при проектировании БЗ для НР на первом этапе предлагаемой технологии на основе глубокого квантовой машинного обучения. На втором этапе объединение множества различных БЗ в КНВ позволяет достигать глобально робастного интеллектуального управления (см. рис. 5).

На рис. 28 проиллюстрирована взаимосвязь ГРИД-технологий и суперкомпьютинка в задаче проектирования интеллектуальной системы управления. Показана тесная зависимость верификации и идентификации ОУ с применением технологий аналитики и обработки больших данных (Big Data) и кластеризации продукционных правил в БЗ интеллектуальных регуляторовна основе выделения и поиска информативных признаков (на этапах проектирования БЗ с использованием моделирования на суперкомпьютере).

Суперкомпьютинг

Определение диапазонов для поиска, параметров модели ОУ

Поиск значений параметров модели

Поиск оптимальных

Этап 1. Технологии проектирования ИСУ

Определение структуры модели описывающей представление о

траектории изменения коэффициентов усиления регулятора

Проектирование БЗ с применением модели ОУ. И инструментария

Загрузка БЗ в HP вычислительного элемента системы и оценка адекватности динамики системы модели и объекта управления

HP для управления в режиме реального времени

Рис. 28. Структура суперкомпьютинга на ГРИД технологии в интеллектуальном управлении физической установкой

Особенностью предлагаемой технологии является использование непосредственно физической установки для формирования и получения обучающего сигнала. При этом основой такой технологии являются эвристические эволюционные алгоритмы с дискретными ограничениями.

Рассмотрим подробнее процесс функционирования подобной системы (см. рис. 29).

Сенсорная система физической установки (пикапэлектроды и др.) считывает показания физического эксперимента и пересылает их в вычислительное устройство для последующей обработки. Приняв входные значения, ОБЗ оценивает эффективность предыдущего решения (загруженной БЗ НР) и осуществляет формирование новой или корректировку используемой базы знаний для проверки следующего решения (БЗ НР), при этом возможен гибридный подход с применением суперкомпьютинка для формирования как индивидуальной БЗ, так и иерархически связанных БЗ многоагентной системы. Результат нечёткого логического вывода отправляется на удалённое устройство. После этого, система управления, обработав входные значения, вырабатывает управляющее воздействие. Прежде чем приступить к установке соединения между ОБЗ и системой управления необходимо установить физические ограничения взаимодействующих устройств, т. е. определить максимальные и минимальные временные границы, величину одной итерации с учётом приёма, передачи и обработки информации.

Результаты проведенных исследований показали, что для проектирования качественной и робастной ИСУ недостаточно использовать только математическую модель или реальный ОУ в отдельности. Совместное использование полученных от данных моделей БЗ как информационных ресурсов (в виде извлеченной скрытой квантовой информации в классических управляющих сигналах) дает дополнительный синергетический эффект в виде повышения качества управления и робастности проектируемых ИСУ. Данный эффект отсутствует в отдельно используемых БЗ и из которых извлекалась дополнительна скрытая квантовая информация. Открытый синергетический эффект носит по природе своей квантовый характер, является результатом квантовой самоорганизации классических БЗ и не может быть получен классическими методами исчисления.

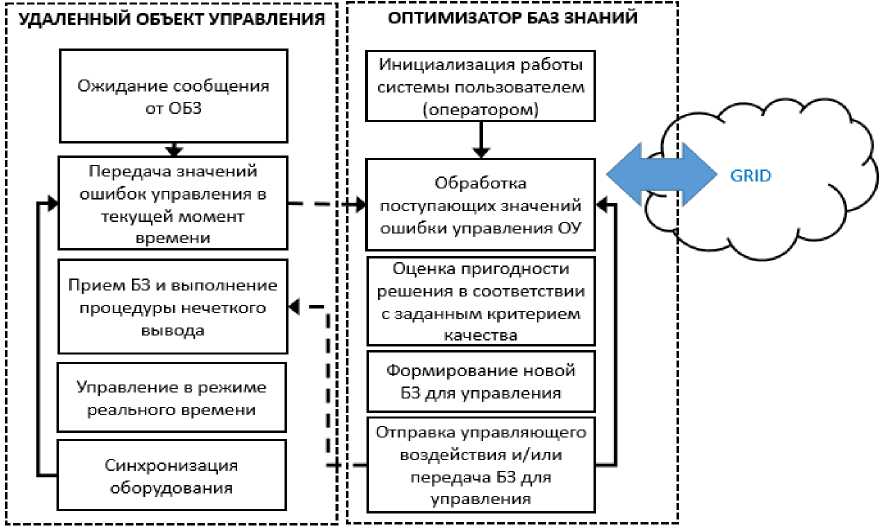
GRID

УДАЛЕННЫЙ ОБЪЕКТ УПРАВЛЕНИЯ

ОПТИМИЗАТОР БАЗ ЗНАНИЙ

Синхронизация оборудования

Управление в режиме реального времени

Передача значений ошибок управления в текущей момент времени

Прием БЗ и выполнение процедуры нечеткого вывода

Ожидание сообщения от ОБЗ

Обработка поступающих значений ошибки управления ОУ

Оценка пригодности решения в соответствии с заданным критерием ________ качества ________

Формирование новой БЗ для управления

Отправка управляющего воздействия и/или передача БЗ для управления

Инициализация работы системы пользователем (оператором)

Рис. 29. Структура применения оптимизатора баз знаний в интеллектуальном управлении физической установкой на ГРИД технологии

Оптимизация БЗ с использованием дистанционного соединения с ОУ непосредственно напрямую с ОБЗ даёт ряд преимуществ:

• -    позволяет не разрабатывать математическую модель и при этом получать знания о качественном поведении ОУ для построения БЗ;

• -    для проектирования ИСУ в ОБЗ достаточно снять информативные показатели и параметры поведения ОУ;

• -    дистанционное соединение позволяет оптимизировать БЗ в определённых (типовых) условиях функционирования, и тем самым создавать множество БЗ с высоким качеством управления для различных ситуаций управления.

С точки зрения программной инженерии, БЗ реализована структурным типом данных и ее размерность зависит от количества входных и выходных переменных, количества функций принадлежности лингвистических переменных и количества продукционных правил. В этом смысле ОБЗ, как универсальный аппроксиматор, имеет ряд преимуществ по объему передаваемых данных и минимизацией загрузки каналов передачи.

Отметим, что универсальность технологии дистанционной настройки и передачи баз знаний (БЗ) позволяет объекту управления (ОУ) принимать БЗ от блока ОБЗ, или от других ОУ. Это даёт возможность управления структурно новыми объектами, такими как коллективы роботов, многоагентные системы, сложные автоматизированные производства и распределенные системы др. Кроме того, данная технология позволяет ОУ обновлять и адаптировать БЗ под конкретную ситуацию управления, в т.ч. нештатную ситуацию, непосредственно в режиме реального времени функционирования.

Разработанный инструментарий реализует механизмы создания, настройки и передачи параметров управления в виде сигналов управления, полученных из БЗ НР, не разрушая нижний исполнительный уровень. Использование квантовых мягких вычислений и разработанных технологий проектирования ИСУ сокращает влияние экспертных оценок в процессе обучения и настройки ИСУ. Снижает информационный риск влияния человеческого фактора на принятие решения в условиях возникновения нештатных ситуаций или непредвиденных ситуаций управления.

Заключение

На комплексе NICA развивается широкая программа научных и прикладных исследований.

В этих условиях эффективное решение задачи создания интеллектуальной системы управления комплексом NICA подразумевает взаимодействие научно-исследовательских групп ОИЯИ, а также применение интеллектуальных вычислений и «робастных» сквозных квантовых технологий технологий, представляющих собой совокупность методов классической и квантовой теорий управления, которые обеспечивают необходимое качество управления, даже если объект управления отличается от расчётного или его математическая модель неизвестна.

Для управления комплексом NICA предлагается решить следующие задачи:

• -    Разработать и реализовать двухуровневую гибридную интеллектуальную систему управления.

На нижнем уровне осуществляется сбор, обработка и хранение информации для формирования управляющего воздействия на исполнительные устройства ( Tango Controls ), а на верхнем уровне (ИСУ), формируется воздействие на исполнительные механизмы ускорителя NICA , реализуются дополнительные обратные связи управляющих контуров для поддержания режима функционирования системы в автоматическом режиме с повышенным уровнем робастности.

• -    Формирование такой системы позволит повысить эффективность работы комплекса NICA, понизить потери полезного ресурса (электроэнергии и времени) и потребует минимальной исходной информации для выработки управляющего воздействия.

• -    Разработка верхнего уровня ИСАУ позволит решить задачи гарантированного достижения цели управления и обеспечить получение ожидаемого результата в различных режимах работы ускорителя.

• -    В этом случае, очевидно, необходимость разработки принципов и основ новой ИТ проектирования систем искусственного интеллекта (ИИ) с применением квантовой релятивистской информатики, распределенных высокопроизводительных вычислительных систем типа ГРИД-технологий для решения задач интеллектуального управления физическими установками НИКА и им подобных.

• -    Программно-алгоритмическую платформу поддержки интеллектуальной системы управления осуществить на основе теории искусственного интеллекта (с применением разработанной базы глубокого квантового машинного обучения и оптимизации управления на основе квантовых генетических алгоритмов с применением оптимизаторов баз знаний на квантовых / мягких вычислениях).

• -    В частности необходимо:

• -    разработать платформу программно-алгоритмической поддержки информационной технологии для процессов моделирования и проектирования робастных самоорганизующихся интеллектуальных систем управления ускорительным комплексом, способных функционировать как в штатных, так и в нештатных ситуациях управления;

• -    создать программно-алгоритмический комплекс на основе сквозных квантовых технологий распределенных вычислений – ГРИД-технологий, квантовых поисковых алгоритмах, суперкомпьютинга в рамках задач поиска, сбора и обработки распределенных данных (типа Data Lake ) для проектирования самоорганизующихся интеллектуальных систем управления на платформе технологий квантовых мягких вычислений.

• -    Не менее важной задачей в современных условиях проектирования и эксплуатации ускорительных установок в мегапроекте NICA является подготовка высококвалифицированных специалистов, инженеров в области интеллектуальных ИТ и самоорганизующихся систем интеллектуального управления.

• -    Разработка научного базиса новых образовательных квантовых технологий для проектирования робастных интеллектуальных систем управления слабоструктурированными физическими мегаустановками является необходимой и неотъемлемой частью создания и внедрения представленных технологий.