Возможности прогностических систем проспективной оценки результата лечения рака мочевого пузыря
Автор: Зимичев Александр Анатольевич, Чернышев Игорь Владиславович, Хрисанов Н.Н., Климентьева М.С.
Журнал: Хирургическая практика @spractice
Рубрика: Оригинальные исследования
Статья в выпуске: 4, 2016 года.
Бесплатный доступ
В результате исследования разработана нейронная сеть прогноза результата лечения рака мочевого пузыря, позволяющая с высокой степенью достоверности предсказать исход лечения. При прогнозе рака мочевого пузыря целесообразно применять трехслойную сеть с количеством нейронов в выходном слое равном возможному числу исходов заболевания. С помощью нейронной сети возможно выбрать оптимальную тактику лечения, меняя величину вектора входного слоя нейронов и оценивая величину выходного вектора.
Рак мочевого пузыря, нейронная сеть, отдаленные результаты лечения
Короткий адрес: https://sciup.org/142211686
IDR: 142211686
Текст научной статьи Возможности прогностических систем проспективной оценки результата лечения рака мочевого пузыря
Необходимость выбора оптимальной адъювантной терапии, стандартизации и оптимизации послеоперационного диспансерного наблюдения за пациентами определяет актуальность поиска новых, более совершенных прогностических систем на основании доступных и достаточно простых клинических и лабораторных критериев. Такую возможность дает применение нейросетевого анализа данных и моделирования, которое отличается высокой прогностической точностью, не уступая традиционным методам математического моделирования – таким как многофакторный корреляционно-регрессионный анализ. Прогноз основывается на матрице данных реальных клинических случаев, что определяет его высокую прикладную ценность.
Нейронные сети представляют собой нелинейные системы, позволя-ющие гораздо лучше классифицировать данные, чем обычно используемые линейные методы. Нейросети оказались способными принимать решения, основываясь на выявляемых ими скрытых закономерностях в многомерных данных. Отличительное свойство нейросетей состоит в том, что они не программируются – не используют никаких правил вывода для постановки диагноза, а обучаются делать это на примерах. Для искусственных нейронных сетей под обучением понимается процесс настройки архитектуры сети (структуры связей между нейронами) и весов синаптических связей (влияющих на сигналы коэффициентов) для эффективного решения поставленной задачи.
Применение нейронных сетей дает ряд преимуществ по сравнению с традиционным подходом к решению подобных задач, позволяя:
-
1) одновременно учитывать большое количество влияющих параметров, воздействующих на множество зависимых величин;
-
2) по имеющимся базам данных автоматически синтезировать высоко-сложные аналитические модели, наиболее полно отражающие характерные для исследуемой системы причинно-следственные связи между влияющими и зависимыми параметрами;
-
3) автоматически оценить степень влияния каждого из множества воздействующих параметров на зависимые величины;
-
4) корректировать полученную аналитическую модель с появлением новых данных путем «доучивания» нейронной сети.
Аналитические модели представляют собой матрицу коэффициентов, используемых в уравнениях функционирования формальных нейронов. В программных реализациях нейронных сетей достаточно указать полученную матрицу в качестве параметров модели, чтобы получить прогнозы зависимых величин. В этих же матрицах нейронной сетью закладывается информация о степени влияния каждой из независимых величин на зависимые в виде коэффициентов. Для оценки степеней влияния в долях или процентах каждый из коэффициентов делится на их общую сумму.
Однако, несмотря на все преимущества, обеспечиваемые нейросетевой моделью, при таком подходе также имеется ряд недостатков:
-
– структуру сети и ее обучение необходимо проводить под каждый конкретный класс заболеваний;
-
– в связи с большим количеством параметров и полносвязан-ностью сети задача имеет высокую вычислительную мощность;
-
– сложность или невозможность решения обратной задачи (по данным исхода лечения определить исходные данные).
Задача прогнозирования лечения рака мочевого пузыря относится к классу трудноформализуемых задач, то есть таких, для которых алгоритм решения либо не является единственным, либо не позволяет оценить качество или достижимость решения. Для принятия правильных тактических решений в процессе лечения и последующих реабилитации и наблюдения необходимо анализировать большое число различных данных одновременно. Влияние каждого из этих факторов на исход лечения неоднозначно и нелинейно. Для облегчения практического решения подобных задач многофакторного анализа, моделирования и прогнозирования отдаленных результатов мы использовали нейронные сети.
Материал и методы исследования
Для прогнозирования исхода лечения рака мочевого пузыря разработана нейронная сеть, определяющая результат лечения рака мочевого пузыря в зависимости от эпидемиологических, клинических факторов, морфологических особенностей опухоли и подхода к лечению (4).
Исходным материалом исследования служили 546 пациентов, получавших лечение в клинике урологии СамГМУ в период 2000–2010 гг (5,6).
Условно исход заболевания поделен на благоприятный – пятилетняя безрецидивная выживаемость, сомнительно благоприятный – пятилетняя выживаемость с рецидивом, неблагоприятный – летальный исход вследствие генерализации опухолевого процесса, и каждаму типу исхода присвоено цифровое дискретное значение 1, 2, 3.
В качестве входного слоя нейронов использованы следующие параметры пациентов: пол, возраст, профессиональные вредности в анамнезе, время, прошедшее с момента заболевания, курение сигарет, алиментарные особенности, водный режим, генетическая детерминация опухолевого новообразования, заболевания, приводящие к инфравезикальной обструкции, воспалительные заболевания мочеполовой системы, стадия рака мочевого пузыря, гистологическая характеристика опухоли, глубина инвазии, наличие инвазии в венозные и лимфатические сосуды, локализация и размер новообразования, характер роста, количество опухолей, функциональное состояние почек, характер лечения, степень регрессии опухоли после неоадъювантной полихимиотерапии, характер оперативного пособия, использование нестандартных приемов и инструментов, наличие рецидивной опухоли. Каждому признаку присвоено то или иное цифровое дискретное значение в зависимости от степени его проявления.
Задача прогноза исхода (результата) лечения по набору входящих параметров является обобщением классической задачи аппроксимации функций. Анализ некоторых работ (2,3) показал, что для решения поставленной задачи можно воспользоваться алгоритмом обратного распространения ошибки, используя следующие архитектуры нейронных сетей – многослойный персептрон и сеть с общей регрессией (GRNN).
Результаты и обсуждение
Для моделирования и решения задачи предсказания результата лечения рака мочевого пузыря использовалась нейронная сеть, архитектурное решение которой реализовано в виде многослойного (трехслойного) персептрона. В нейронной сети каждый элемент вектора входа (для входного слоя это вектор p , для остальных вектор a i , где i – номер предыдущего слоя) соединен со всеми входами нейрона и это соединение задается матрицей весов IW 11 для входного слоя и матрицей LW ij для остальных слоев. При этом каждый i -й нейрон включает суммиру ющи й элемент, который формирует скалярный выход n ( k ), k = 1 - S i . Совокупность скалярных функций n ( k ) объединяется в S i элементный вектор входа n i функции активации i -го слоя f i . Выходы слоя нейронов формируют вектор столбец a i , и, таким образом, описание слоя нейронов имеет вид:
n = f ( Wp + b ), (1)
-
S 1 = S 2 = R – размер входного вектора (исходные факторы и параметры); S 3 = 1 – 4 – размер выходного вектора (результат лечения).
В качестве функции активации используется антисимметричная сигмоидальная функция вида:
f ( x ) = —-- 0,5. (2)
-
1 + e a x
Производная функции активации f (x ) = af (x )(1- f (x))-
Программа, реализующая нейронную сеть, написана на языке Basic в среде приложения Calc офисного пакета OpenOffice. org. Программа, реализующая нейронную сеть, имеет следующие модули: модуль предварительной обработки и нормализации экспериментальных данных; модуль обучения нейронной сети; модуль диагностики.
С помощью модуля предварительной обработки производится выявление противоречащих друг другу экспериментальных данных, исключение повторяющихся выборок, нормализация исходных данных (Ганцев Ш.Х. и др., 2010). Нормализация заключается в приведении исходных данных к линейному участку функции активации, а именно к диапазону 0,5 ... 0,5. Подобная нормализация позволяет значительно повысить скорость сходимости алгоритма обучения нейронной сети.
Как только начальные веса и смещения нейронов установлены пользователем или с помощью датчика случайных чисел, сеть готова для того, чтобы начать процедуру ее обучения. Сеть может быть обучена решению различных прикладных задач – аппроксимации функций, иденти-фикации и управления объектами, распознавания образов, классификации объектов и т. п. Процесс обучения требует набора примеров ее желаемого поведения – входов p и выходов t. С учетом специфики многослойных нейронных сетей для них разработаны специальные методы обучения и подбора и настройки весов связей, среди которых следует выделить метод обратного распространения ошибки. Этот алгоритм реализует модуль обучения программы. В процессе обучения используется выборка из экспериментальных данных, включающих набор входов p и желаемых целевых выходов t. Во время этого процесса веса IW11 и смещения b настраиваются так, чтобы минимизировать некоторый функционал ошибки. Как правило, в качестве такого функционала для сетей с прямой передачей сигналов принимается среднеквадратичная ошибка между векторами выхода a и t:
Q S M 2
J = 1 t q - * И , (3)
2 ii q = 1 i = 1
где J – функционал; Q – объем выборки; M – число слоев сети; q – номер выборки; S M – число нейронов выходного слоя; a q = |^ aiM J - вектор сигнала на выходе сети; t q = ^ t q J - вектор желаемых (целевых) значений сигнала на выходе сети для выборки с номером q (Ганцев Ш.Х. и др., 2010).
Рассмотрим выражение для градиента критерия качества по весовым коэффициентам для выходного слоя М :
После подстановки (6) в (4) имеем:
J M" = - f ( t q - < ) f^A< ) a qq*M - 1) . (7)
j.j q = 1
Если S M равен 1 (количество нейронов в выходном слое равно 1), то
J = — t ( tq - < ) ЛД < ) a ( M - 1) . 5to j j q = 1
Если обозначить
ДqM =(ti - aqlM то получим
∂ J
∂ω iMj
Q
= - £ A qM a qM - 1) , i = 1, S M , j = 0, S M - 1
q = 1
.
Аналогично выводятся соотношения для настройки весов ω i M j - 1 слоя M -1:
d J
,) Q s M q./
- < ) 2 =- zz ( t q - < yOM- , (4)
q = 1 k = 1 O j
где Q – объем выборки; S M – число нейронов в слое; ak qM – k -й элемент вектора выхода слоя М для элемента выборки с номером q ; i – номер нейрона; j – номер входа.
Если S M равен 1 (количество нейронов в выходном слое равно 1), то
Q S M
—°— = V qtq _aqM
M - 1 Z^^\ t k a k
O^ j q _ 1 k _ 1
Q S M
_- ZZ ( tk - akM ) Л.Д"
q = 1 k = 1
Q
_-£a q(M-1) aq M to ki где Правило функционирования слоя М: qM k ( sM—1 s l=0 M q (M-1) к_л MM tvki ai , где k — 1, s . Если SM равен 1 (количество нейронов в выходном слое рав- но 1), то qM a ( SM 4 X l=0 to, l aqq (M4) 6n qM r)a4 (M-1) dnk dak q (M-1) _ daq(M-1) dmM"* Qi d n4kM dai(M-1) q(M-1) q(M-2) _ SM aq(M-1) = I (tk - aqM) fM (nkM) ® MfM-1 (nq(M-1) / k=1 (SM ^ = I a kM ni(M-1)), где i = 1, SM-1. Для слоев М-2, М-3,…,1 вычисление частных производных критерия J по элементам матриц весовых коэффициентов выполняется аналогично. В итоге общая формула будет выглядеть следующим образом: Q dJT = -Z Aq^aq r , r = 1, M,1,5r, j = 0,5r , (12) Stoj q=1 где r – номер слоя Из уравнения (4) следует: d aqM dj k * i ----- ------- , i = 1, SM, j = 0, SM-1. k = i Д qr = ^ fr ‘(nq ), r = 1, M -1 ^ Sr+1 Z д q(r+1)» y к=1 д qM „ q ( m-1) aj Алгоритмы обучения, как правило, функционируют пошагово; и эти шаги принято называть эпохами или циклами. На каждом цикле на вход сети последовательно подаются все элементы обучающей последовательности, затем вычисляются выходные значения сети, сравниваются с целевыми и вычисляется функционал ошибки. Значения функционала, а также его градиента используются для корректировки весов и смещений, после чего все действия повторяются. Начальные значения весов и смещений выбираются случайным образом, а процесс обучения прекращается, когда выполнено определенное количество циклов либо когда ошибка достигнет некоторого малого значения или перестанет уменьшаться. Для нейронной сети форма позволяет задать количество слоев, объем выборки Q и размер входного вектора наблюдений R, количество нейронов в каждом слое, выбрать тип функций активации для каждого слоя (сигмоид или линейная) и задать ее параметры. Для процесса обучения задается максимальное число циклов (эпох), точность аппроксимации как максимальная разница значений критерия для двух последних итераций, скорость обучения. Также указывается, используется или нет в процессе обучения вектор смещения bi. В левой части формы в процессе обучения выводится значение критерия для каждой пятой итерации. В процессе обучения использовалась генеральная совокупность 546 пациентов, прошедших лечение по поводу рака мочевого пузыря. Случайным образом из генеральной совокупности была сформирована обучающая выборка из 120 примеров. Оставшиеся 426 примеров вошли в проверочную (контрольную, тестовую) выборку. Количество нейронов во входном и промежуточном слоях было равно размерности входного вектора, R = S1 = S2 = 18. Количество нейронов в выходном слое S3 = 3, то есть равно возможному числу исходов лечения. Поскольку для двухслойной сети после 80-й итерации наблюдается явление переобучения сети. Для двухслойной сети после 80-й итерации наблюдается явление пере- обучения сети. При этом ошибка распознавания на тестовой выборке составила около 10%. Для трехслойной сети явление переобучения не наступало до 600-й итерации. При этом погрешность распознавания на тестовой последовательности составила менее 4%. Заключение Таким образом, моделирование прогноза результатов лечения рака мочевого пузыря с помощью нейронной сети позволяет с высокой степенью достоверности предсказать конечный результат. При этом целесообразно применять трехслойную сеть с количеством нейронов в выходном слое равном возможному числу исходов курса лечения. С помощью нейронной сети возможно выбрать оптимальную тактику лечения, меняя величину вектора входного слоя нейронов и оценивая величину выходного вектора.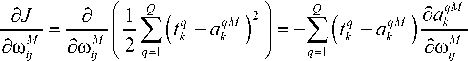
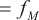
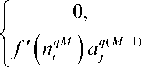
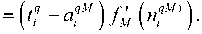
Список литературы Возможности прогностических систем проспективной оценки результата лечения рака мочевого пузыря
- Барский А. Б. Нейронные сети: распознавание, управление, принятие решений. -М.: Финансы и статистика, 2004. -176 с.
- Медведев В.С., Потемкин В.Г. Нейронные сети. MATLAB 6. М.: ДИАЛОГ-МИФИ, 2002. -496 с.
- Хайкин, Саймон. Нейронные сети: полный курс, 2-e издание.: Пер. с англ. М.: Издательский дом "Вильямс", 2006. 1104 с.
- Нейронная сеть для определения исхода лечения рака мочевого пузыря и рака предстательной железы/А.А. Зимичев, Н.Н. Хирсанов, С.Е. Коновалов, М.С. Климентьева. Свидетельство о государственной регистрации программы для ЭВМ № 2010614903 от 28.07.2010.
- Ш.Х. Ганцев, А.А. Зимичев, Н.Н. Хрисанов, М.С. Климентьева Применение нейронной сети в прогнозировании рака мочевого пузыря///Медицинский вестник Башкортостана. -2010. -№ 4. -С. 34-37.


