Возможности развития метода преобразования структурных схем в задачах динамики виброзащитных систем (часть I)

Структурное математическое моделирование находит достаточно широкое применение в задачах динамики машин, особенно в тех направлениях, которые связаны с исследованиями вибрационных процессов [1 - 4]. В рамках таких подходов исходная механическая система отображается расчетной схемой в виде механической колебательной системы, той или иной сложности, с последующим построением структурной модели на основе теории графов, теории цепей или теории автоматического управления. Построение структурной модели может производиться непосредственно по расчетной схеме или через предварительное составление математической модели в виде системы линейных дифференциальных уравнений. Для реализации соответствующих технологий построения структурных моделей используются преобразования Лапласа [5, 6]. Технология построения структурных математических моделей в детализированном виде нашла отражение в работах [7 - 10]. Вместе с тем ряд вопросов, связанных с преобразованиями структурных моделей, особенно при наличии непланарных и перекрестных связей, еще не получил должной детализации представлений, что стимулирует развитие исследований, особенно в приложениях к системам трех и более степеней свободы.

В предлагаемой статье метод структурных преобразований развивается в направлении учета особенностей межкоординатных связей в системах с тремя степенями свободы при наличии в структурах замкнутых контуров.

Общие положения. Постановка задачи исследования

В качестве исходной расчетной схемы рассматривается механическая колебательная линейная система цепного типа с тремя степенями свободы с сосредоточенными параметрами (рис. 1). Такие расчетные схемы используются, например, в задачах динамики вибрационной защиты машин, приборов и оборудования [6 - 8]. В качестве внешних возмущений принимаются силовые гармонические воздействия Qi ( i = 1,3 ). Кроме того, возможен учет действия кинематических возмущений z k (к = 1,2 ), связанных с опорными поверхностями I и II (рис. 1). В качестве основной выбрана неподвижная система координат y 1 , y 2 , y 3 ; силы трения считаются пренебрежимо малыми, а движение элементов массами m 1 , m 2 , m 3 происходит по вертикали; через k 1 , k 2 , k 3 , k 4 , k 5 обозначены коэффициенты жесткости линейных упругих элементов. Контур I на рисунке 1 определяет размещение виброзащитного устройства (ВЗУ); объект защиты имеет массу m 3 . Опорная поверхность II вводится для построения более полной схемы: при необходимости k 4 и k 5 , так же как Q i и z k , могут принимать нулевые значения. Запишем выражения для кинетической и потенциальной энергий:

T = -т У 1 +- m 2 у 2 +- m з Уз ;

П = 1 k i ( У 1 - Z 1 ) 2 + 1 к 2 ( У 2 — У 1 ) 2 + 1 к з ( У з — У 2 ) 2 + | к 4^ У 3 - Z 2 ) 2 + | к 5^ У 3 - У 1 ) 2 .

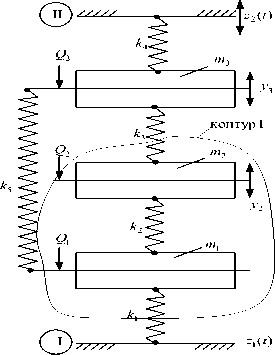
Рисунок 1 – Расчетная схема виброзащитной системы с тремя степенями свободы

Для построения математической модели используется стандартная методика [9, 10] на основе формализма Лагранжа:

^т 1 ^У 1 ⁺ У 1^{( к} 1 ^{+ к} 2 ^{+ к} 5 ) ^{- к} 2 У 2 ^{- к} 5 У 3 = ^Q 1 ^{+ к} 1 ^z i ;                       ⁽³⁾

m 2 ^У 2 ⁺ У 2 ^{( к} 2 ^{+ к} 3 ) - ^к 2 У 1 - ^к 3 У 3 = Q 2 ;

^тзУз + У з ( к з + к ₄ + к ₅) - к₃У ₂ - к₅У ₁ = Q ₃ + к₄г ₂.                   (5)

Если принять, что z 1 = 0, z 2 = 0, а Q 1 ≠ 0, Q 2 ≠ 0, Q 3 ≠ 0, то связи между переменными y 1 , y 2 , y 3 и Q 1 , Q 2 , Q 3 в операторной форме могут быть представлены в виде следующих выражений [10]:

_ Q1(a22a33  a23a32) + Q2(a13a32  a33a12) + Q3 (a12a23  a13a22) .                         (an У1 =                                     .                                    ;                          (6) 1                                    A0 _ Q1(a23а31 - а21 a33) + Q2(a11 a33 - а13а31) + Q3(a13a21 - a11 a23) , У 2 =                                  .                                  ;                         (7) A0 - _ Q1(a21 a32 - a22a31) + Q2(a12a31 - a11a32) + Q3 (a11 a22 - a12a21) У 3 =                                    ,                                    ,                           (8) A0 где A0 = ацa22a33 - ацa23a32 - a33a12a21 - a22a13a31 + a13a21a32 + a12a23a31                      (9) является характеристическим уравнением системы (система симметрична: ах2 = а2и а13 = а3 ^ а23 = a32 ); значок (-) означает изображение по Лапласу, так как по отношению к (3)-(5) для дальнейших расчетов применяется преобразование Лапласа.

Используя (6) - (8), можно построить необходимые передаточные функции. Структурная схема системы, соответствующая уравнениям (3) - (5), приведена на рисунке 2.

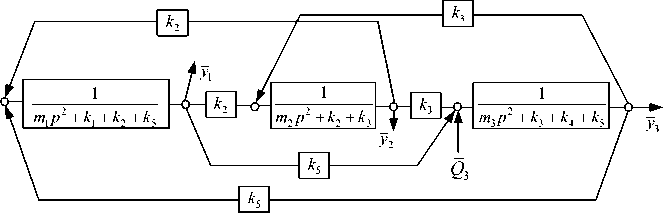
Рисунок 2 – Структурная схема для виброзащитной системы на рисунке 1 при Q 3 ≠ 0

При действии внешних возмущений динамические реакции возникают между объектом защиты m 3 и опорой II , а также между промежуточным инерционным элементом m 1 , ВЗУ и опорной поверхностью I . Динамические реакции будут возникать также и между отдельными элементами системы.

Структура системы (см. рис. 2) состоит из трех парциальных блоков ( mp ² + k_x + k ₂), ( m₂p ² + k ₂ + k ₃), ( mp ² + k₃ + k ₄), между которыми имеются упругие межпарциальные связи k 2 , k з , k 4 . В выражениях (6) — (9) соответственно принято, что a j = m_xp ² + k_x + k ₂ + k ₅, a _{2 2} = m₂p + k ₂ + k ₃, a _{3 3} = m^p + k ₃ + k ₄ + k; , a_{x 2} = a ₂1 = — k ₂, а ^₃ = а з i = — k; , a ₂ з = а з ₂ = — k^ . Структурная схема на рисунке 2 отражает наличие в механической колебательной системе прямых и обратных связей, которые формируют определенные структуры, расширяющие представление о возможностях рассмотрения в качестве парциальных образований следующих видов: [ mm ] = а_па ₂₂ — a 2 , [ mm ] = a₂₂a ₃₃ — a 2₃ , [ mm ] = a_na ₃₃ — a_{x 3}.

Задачей исследования является разработка метода построения математических моделей в задачах вибрационной защиты, использующего характерные особенности исходных систем, учитывающих специфику формирования динамических взаимодействий между элементами с использованием понятий о динамических жесткостях, квазипружинах и обратных связях.

Оценка динамических свойств системы

Используя выражения (6) — (8), можно получить передаточные функции между входными сигналами в виде внешних силовых возмущений Q , Q , Q и соответствующими выходными сигналами – y 1 , y 2 , y 3 . Координаты y 1 , y 2 , y 3 отражают положение системы в координатах, связанных с неподвижным базисом. В дальнейших рассмотрениях полагается, что передаточные функции отражают связи только между двумя точками, т.е. без совмещения действия одновременно двух и более возмущений. В частности при обозначении действия силового фактора, например Q , в выражении для передаточной функции принимается, что Q 2 = 0, Q 3 = 0 и т.д.

соответственно.

Рассмотрим необходимые соотношения для случая k5 = 0, что предполагает отсутствие в рассматриваемой системе замкнутого контура, (т.е. а13 = а31 = 0), тогда где A = апа22а33

^а 11 ^а 23

^а 33 ^а 21

w,( p ) = Ут = ^а a ;

Q ₃     A ₁

₌ У 2 ₌ ^{— а} 11 ^а 23 .

^Q 3       ^A 1   ^;

W 3 ( p ) =

У 3 _ ^а 11 ^а 22 ^а 12

Q 3        A 1

или

A] = ( m^² + k] + k₂ )( m₂p² + k₂ + k₃ )( m₃p² + k₃ + k₄ ) —

— ( m₃p² + k₃ + k₂ ) k 2 — ( m₃p² + k₃ + k₄ ) k ^ = 0.

Уравнение (13) можно преобразовать и представить в виде

a ₃₃ ( a ₁₁ a ₂₂

^a 12 )   ^a 11 ^a 23   ⁰

или

^a 11 ^a 2²3

^a 11 ^a 22 ^{— a} 22

= 0 .

В свою очередь (14) определяется как

,    ₂   ,    , А  ( m^p ² + k + k ₂) k 2   л

( m з p ² + k з + k 4 ) - —^{1   27 3} = 0,

[ mm J где [mm2 J = (mxp2 + kx + k2)(m2p2 + k2 + k3) - k2 .

Структурная схема на рисунке 3, с учетом того, что k 5 = 0, может быть преобразована в

б)

в)

несколько приемов, как показано на рисунке 3. а)

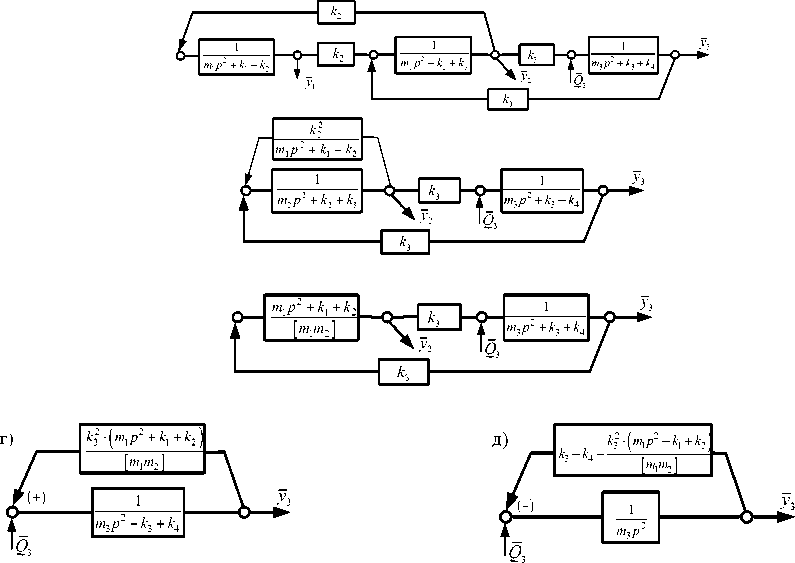
Рисунок 3 – Варианты преобразования структурных схем при выборе объектом виброзащиты массоинерционного элемента m 3 : а – структурная схема системы при k 5 = 0;

б – структурная схема при исключении координат y ; в – структурная схема при выделении парциального блока [ m 1 , m 2 ]; г – структурная схема при выделении квазиупругого элемента или квазипружины; д – структурная схема с выделением объекта защиты m 3

Структурные преобразования исходной схемы на рисунке 3 а показывают, что расчетная схема на рисунке 1 может быть свернута до схемы в виде системы с одной степенью свободы, состоящей из объекта защиты массой m3, двух блоков из упругих элементов (k3 + k4) (рис. 3 д) и квазипружины с динамической жесткостью, определяемой выражением kпр ( P ) = kпр

k² ( m_xp ² + k_x + k ₂)             k ₃ ² ( m_xp ² + k_x + k ₂)

[ mm J      = ( mp ² + k_x + k ₂)( m₂p ² + k + k ₃) - k ² "

Динамическая жесткость квазипружины k пр ( р ) зависит от параметров системы k 1 , k 2 , k 3 , k 4 , m 1 , m 2 , а также от частоты внешнего воздействия.

Структурная схема виброзащитной системы на рисунке 3 д может быть названа базовой, в том смысле, что она отражает свойства исходной базовой расчетной схемы, состоящей из объекта защиты m3 и упругих элементов (k3 + k4) и kпр , работающих параллельно. Отметим, что квазипружина, если иметь в виду правила соединения элементов системы между собой, обладает всеми свойствами обычной пружины. Таким образом, базовая расчетная схема виброзащитной системы определяется наличием двух базовых элементов – объекта защиты (массоинерционный элемент m3) и обобщенной пружины с общей динамической жесткостью kпр(р) = k„р = k3 + k4 + kпр = (k3 + k4)[mm2] + k32

[ mm₂ J

Оценка динамических свойств системы с использованием приведенных параметров жесткости

Динамическая жесткость базовой модели k^ (р) определяется параметрами структурного образования [mm₂ ], которое можно рассматривать как парциальную систему обобщенного вида. Такая структура в механических колебательных системах с несколькими степенями свободы выполняет те же функции, что обычная парциальная система.

Обобщенная парциальная система включает в свой состав обычные системы. Оба вида систем могут находиться одновременно в составе выражений для определения динамических жесткостей квазипружины различного уровня, например, kпр (p) и kпр (p).

В рассматриваемом случае на уровне простых парциальных систем, судя по структурной схеме на рисунке 3 а, имеется три парциальных частоты первого уровня, определяемые выражениями

„ 2 _ k 1 + k 2 .	(19)
n1                  ;
m1
2   k. + k3	(20)
n 2               ;
m 2
7   k. + k.
и2 — 3    4	(21)
^3                 .
m3

Для обобщенной парциальной системы [m,m2] парциальные частоты будут определяться из решения частотного уравнения mm.p4 + p2 [ mx (k2 + k3) + m2 (kx + k2)] + k.k. + k2k3 + kxk3 — 0

или

4,2/2,  2x ,  22    ^k2    _n

p + p (n_x + n₂) + n n₂--²— = 0 .

mm

Динамическая жесткость квазипружины kпр (p), определяемая из выражения (17), имеет два значения частоты внешнего воздействия, когда kпр (p) ^ то, что предполагает появление в исходной системе (или наличие) режимов динамического гашения колебаний. В этих случаях объект защиты m3 будет неподвижным, а его динамическое равновесное состояние будет определяться взаимодействием элементов в обобщенной парциальной системе [mm2 ]. Если ввести в рассмотрение квазипружину второго уровня, определяемую выражением (18), т.е. kпр (p), то можно отметить появление такого динамического свойства, как «обнуление» динамической жесткости. Частоты «обнуления» динамической жесткости определяются из частотного уравнения, получаемого из числителя выражения (18).

mxm2p4 + p 2[ mx (k2 + k3) + m2 (kx + k.)] + (kx + k2)(k2 + k3) - k2 + k 2

+--³— (m_xp²+ k_x + k₂) — 0.

k₃ + k₄           ^{1    2}

При рассмотрении динамической жесткости квазипружины kпр в системе будут наблю- даться совместные движения элементов m1 и m2, которые можно отнести к самоорганизации, характерной для форм движения в свободных колебаниях.

Заключение

Таким образом, структурные математические модели позволяют выделять связи, возникающие между отдельными элементами системы, а также между структурными образованиями, которые по своим обобщенным свойствам могут быть названы квазипружинам. Выделяемые структурные образования можно отнести к обобщенным звеньям механических колебательных систем; получение передаточных функций таких звеньев производится на основе применения правил параллельного и последовательного соединения пружин, а также правил учета введения и реализации обратных связей [9, 10].

Используя структурные схемы исходных механических систем, можно определить динамические жесткости системы в соответствующих точках. В частности интерес представляет определение динамических жесткостей всей системы в целом, поскольку «зануление» этой динамической жесткости совпадает с частотой собственных колебаний, что касается динамических жесткостей отдельных фрагментов системы или ее обобщенных звеньев, то определение условий «зануления» динамических жесткостей в частных случаях, связано с проявлениями различных форм самоорганизации движения. Динамические жесткости отдельных элементов и фрагментов системы могут принимать и бесконечно большие значения, что совпадает с проявлениями таких режимов взаимодействия элементов, как динамическое гашение колебаний.

Во второй части статьи будут представлены результаты исследований, связанных с детализацией представлений о динамических жесткостях и методах определения последних на основе технологий структурных преобразований.

Нумерация формул и рисунков является общей. Библиография отражает ссылки только по материалам второй части статьи.