Возможности совершенствования крутильных весов второго рода

На любую материальную точку массой m на поверхности Земли действует сила тяжести p = mg, где g – ее ускорение. Сила тяжести p определяется геометрической суммой сил притяжения Земли и переносной силы инерции, которая учитывает эффект суточного вращения Земли. В большинстве геофизических задач суточным вращением Земли пренебрегают, так как она дает малый вклад в силу тяжести.

Земная кора неоднородна по своему составу, содержит тела с различной плотностью. В силу этого ускорение силы тяжести g , являющейся силовой характеристикой гравитационного поля Земли, различно как по величине, так и по направлению. Абсолютное значение ускорения силы тяжести в системе координат XOYZ определяется по формуле

g = gx +gy +gz , где gx, gy, gz – проекции g на оси OX, OY, OZ.

Взаимосвязь силовых и энергетических характеристик гравитационного поля следующая:

сW

• g x = W x = д

сW

• g_y = W_y = £_Y ,

сW

• g z = W z =- _{г Z}

где W – потенциал гравитационного поля.

В каждой точке земной поверхности вследствие неоднородной структуры земной коры абсолютное значение ускорения g различно. Относительные изменения ускорения ∆ g от пункта к пункту наблюдений устанавливаются с помощью гравиметров. Эти устройства позволяют обнаружить в земной коре тела с различной плотностью.

Однако гравиметры приблизительно определяют            местоположения исследуемых неоднородностей. Чтобы узнать подробности относительно их формы и геометрического распределения, необходимо       более       детально рассматривать изменения gx, gy, gz в пункте наблюдения. Наиболее полная информация о возмущающем объекте будет, если определить все компоненты вторых производных потенциала W гравитационного поля:

51

W xx    W xy    W xz ,

W yx    W yy    W yz ,

Wzx   Wzy   Wzz , где например W =  gx =  2W где, например, xz “ д      д показывает изменение  gx  в  пункте наблюдения на единицу длины смещения по оси OZ.

Вторые производные характеризуют

Для поиска тел различной плотности необходимо учитывать точность, с которой работают гравиметр и вариометр. Для гравиметра отнсительная

неоднородность поля тяготения, создаваемого телами различной плотности и формы. Вторые производные

измеряются вариометрами.

В качестве примера на рис.1 показаны кривые W xz и ∆ g для бесконечно длинного параллелепипеда [1]. Из рис.1 видно, что вторая производная W xz по max и min кривой очень четко ограничивает

геометрические размеры тела.

Ускорение ∆ g измеряется в мГл, W xz – в

Е, 1 мГл =10–5 м/с2, Е=10-9 с–2.

В принципе измерения W xz и ∆ g могут

погрешность измерения определяется J qmin q1= л , где   Aq  – точность

1      qmax измерения. Относительная погрешность (Л xz min вариометра     q2 = А         ,    где

(      xz ) max

(А W _xz )_min    – точность измерения.

Очевидно, возможности гравиметра и вариометра будут равными, если q1=q2. Определим глубину H залегания неоднородностей,      на      которой существующие точности устройств будут равны. В качестве примера тела, создающего неоднородность, рассмотрим шар, считая массу шара сосредоточенной в его центре. При расчетах использованы

заменить друг друга.

Имеем   W_xz

g x

. Для больших z

теоретические выкладки, изложенные в работе [1].

g max

перемещений  ∆ g=W xz ∙ ∆ x.  Численным

GM

_Н 2 ^,

дифференцированием по кривой  ∆ g

можно построить кривую W xz , и наоборот, численным интегрированием кривой W xz

(А   xz

)

max

2 48 GM

25 V _{5 Н 3} ,   (1)

можно определить кривую ∆ g .

где G – гравитационная постоянная, М – масса шара, Н – глубина залегания шара.

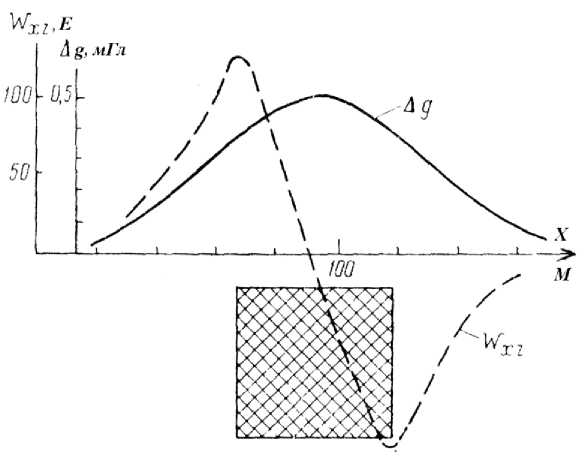
Рис. 1. Кривые ∆g и W xz над бесконечным параллелепипедом

Приравнивая q 1 и q 2 , получаем

A ^q min

A q max

Подставим в (1)

Aq min

GM

Н2

Получим

(   W xz ) min

⁽A ^W xz ⁾ max

(AW)

xz min

2 48GM .

25 л/5Н3

.

В ЭМП ферромагнитное тело устанавливается по оси ОО в верхней части весов. Весы, используемые в ЭМП, значительно усовершенствованы [3], уменьшены их габариты и масса (рис.3).

H=1,71

Aq min

(A W )   , (2)

xz mi n

Для гравиметров A q _min =0,01∙10^–5

градиентометров

–

( W xz ) min = 10^–9

м/с², –2

с

.

Подставляя эти параметры, получим Н = 171 м.

Поскольку точность измерения гравиметра не может быть выше 0,01∙10^–5 м/с², то глубина Н , на которой может эффективно работать вариометр, определяется точностью измерения вариометра ( Д W _xz ) _min . Вопрос для рассмотрения важен, поскольку вариометр дает большую информацию о

залегающем теле.

В работе [2] проведены теоретические и экспериментальные исследования в области разработки вариометров на

основе электромагнитных подвесов (ЭМП). При исследованиях в качестве базового вариометра выбрана модель ГРБ-М2. Точность измерения вариометра ( W xz ) = ±(5–7)Е.

Основным чувствительным элементом являются крутильные весы второго рода. В ГРБ-М2 коромысло крутильных весов подвешивается на крутильной нити вдоль оси ОО (рис. 2).

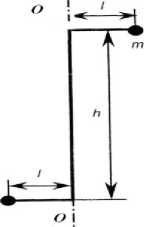
Рис.2. Коромысло крутильных весов второго рода

Рис.3. Весы: 1 – ЭМП; 2 – ГРБ-М2

Если на коромысло крутильных весов действует момент силы W xz = mlh, то угол поворота вокруг оси ОО

A

mlh_{W ,} xz

т

где m – массы грузов, прикрепляемых к коромыслу, l – расстояние грузов от оси вращения, h – длина коромысла, τ – крутильная жесткость нити подвеса или крутильная жесткость в ЭМП.

Предположим, что точность измерения углов ГРБ-М2 и ЭМП одинакова. Проведем сравнительную оценку минимально измеряемого W xz ЭМП.

ГРБ-М2: m = 9,8 г, l = 0,5 см, h = 40 см, τ = 2,5∙10^–1 г∙см²/с²,

⁽A W _xz )_min =5∙10 с .

ЭМП: m = 2,4 г, l = 0,085 см, h = 6,78 см, τ м = 4,28∙10^–7 г∙см²/с².

Правые части уравнения (3) будут одинаковы, т.е. ЭМП дает точность измерения (A W xz ) min , равную 0,001Е. Магнитный подвес повышает точность измерения в 5000 раз. Подставляя полученное значение (A W xz ) min в уравнение (2), имеем

Н = 1,71∙10⁵ м = 171 км.

Глубина обнаружения неоднородостей для градиентометра теоретически составляет 171 км. Такой запас