Возмущение потока при инвазивном измерении давления крови

При оперативных вмешательствах и ведении тяжелых больных необходим постоянный контроль артериального давления. Этот контроль осуществляется за счет введения в сосудистое русло катетера (рис. 1), который представляет собой полую © Булавин Л.А., Кнышов Г.В., Забашта Ю.Ф., Бацак Б.В., Северилов С.В., 2013

Булавин Леонид Анатольевич, академик Национальной академии наук Украины, д.ф.-м.н., заведующий кафедрой молекулярной физики, Киев

Забашта Юрий Феодосьевич, профессор, д.ф.-м.н., преподаватель кафедры молекулярной физики, Киев Бацак Богдан Вадимович, заведующий отделением лучевой диагностики, Киев Северилов Степан Вячеславович, аспирант кафедры молекулярной физики, Киев

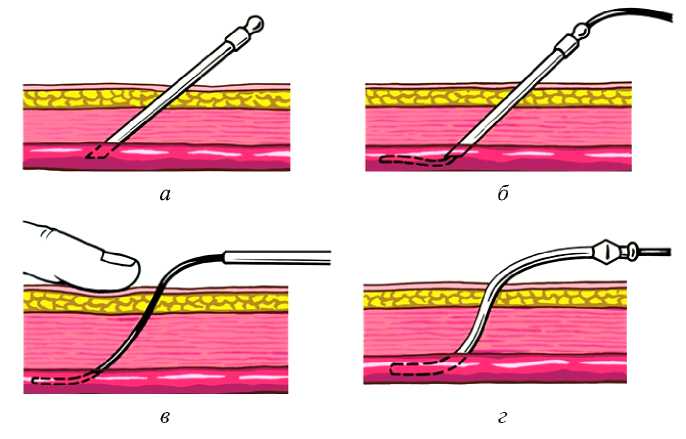
Рис. 1. Катетеризация артериального русла: а – пункция сосуда; б – введение проводника и удаление иглы; в – нанизывание катетера; г – введение катетера в сосуд и удаление проводника полимерную трубку, заполненную раствором гепарина [1]. Катетер соединяется при помощи удлинителя с манометром. Манометр измеряет среднее давление по торцу катетера.

Очевидно, что введение катетера искажает истинную картину кровяного потока и распределения давления в сосуде. Поэтому давление, которое измеряется манометром, отличается от давления при отсутствии катетера. Соответственно изначально в упомянутом методе заложена систематическая погрешность.

Цель работы состоит в том, чтобы теоретически рассчитать данную погрешность. Очевидно, что такой расчет является единственным способом получить оценку указанной погрешности. Как известно авторам, эта задача ранее в литературе не рассматривалась.

Расчетная модель

Будем рассматривать кровеносный сосуд как канал цилиндрической формы в упругой среде. Последняя моделирует собой биоткани, окружающие сосуд. Радиус указанного канала обозначим через b .

Катетер представим в виде полого цилиндра с внутренним радиусом a и внешним a ₁ , заполненного идеальной несжимаемой жидкостью. Поскольку толщина стенки катетера на порядок меньше радиуса, границу катетера далее в расчетах будем считать линией. Материал стенки катетера будем считать абсолютно твердым. Полый цилиндр располагается внутри канала таким образом, что их оси симметрии совпадают (рис. 2).

Сосуд заполнен кровью, которая рассматривается как идеальная несжимаемая жидкость. Течение крови описывается уравнением Эйлера

ρ ^d v = - ∇ p ,                                  (1)

dt при условии

∇ ⋅ v = 0,                                         (2)

где ρ – плотность; v – скорость; t – время; p – давление.

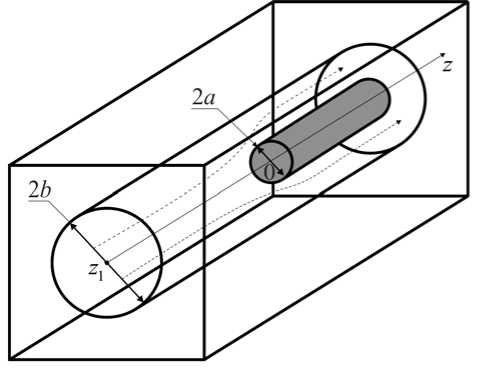
Рис. 2. Расчетная модель: a - радиус катетера; b - радиус упругой среды, моделирующей биоткани, окружающие сосуд

Задача решается в линейном приближении, уравнение (1) примет вид

d v

P/^V p • dt

Введем цилиндрические координаты с осью z , которая совпадает с осью симметрии данной задачи. Пусть торец катетера соответствует координате z = 0. Поскольку задача обладает осевой симметрией, угловая координата выпадает из рассмотрения. Радиальную координату обозначим через r .

Векторные выражения (3) и (2), записанные в компонентах, имеют вид

д vz д t

дp дz ’

д vr    дp

Р             .   ’

д t     б r

^{д v} _z + 1 ^{д ( rv} r ) = 0 д z   r д r

где v_z и v_r – осевая и радиальная компоненты скорости.

На граничных поверхностях z = 0, r <  а и 0 <  z < да , r = а катетера должно выполняться условие

v_n = 0,

где v_n – проекция скорости на нормаль к указанной поверхности. На торце катетера принимается условие v z = 0 из-за того, что внутри катетера пульсовая волна не может распространяться по причине жесткости его стенок.

Обозначим через u = {u_r , u z } вектор смещения, определяемый формулой

d u v =—.

dt

Постулированная ранее упругость стенок канала требует выполнения на его границе r = b условия

P = ^a ur\_r = _b ,                                            (9)

где a - коэффициент упругости среды, окружающей канал.

Поступление крови в сосуд обеспечивает насосная функция сердца. Описать процесс движение крови, направленной в сосуд, можно, например, задавая скорость в сечении, где располагается клапан аорты [4]. Будем считать, что это сечение соответствует координате z1, записывая граничное условие vz (z1, t) = ф(t),                                            (10)

где ф ( t ) - функция, вид которой определяется физиологическими процессами. Ее в рассматриваемой задаче следует считать заданной.

Решив систему уравнений (4)–(6) при граничных условиях (7), (9), (10), можно определить вид функции p ( z , r , t ). Распределение давлений на торце описывается функцией p ₀( r , t ) = p (0, r , t ).

Как уже упоминалось, данная задача состоит в том, чтобы рассчитать давление pт в торце катетера. Фактически pт – это среднее давление, действующее на указанный торец. Это давление определяется формулой p т (t) = -2y fp o( r, t )2n rdr.                              (11)

n a

Применение теории длинных гравитационных волн при изучении течения КРОВИ В СОСУДАХ

Исследование течения жидкости в каналах относится к классическим задачам гидродинамики и имеет долгую историю (например, [2, 3] и др.). За этим научным направлением закрепилось название «теория длинных гравитационных волн». Основу этой теории составляет так называемое гидравлическое приближение [3].

Главным тезисом этого приближения является предположение о том, что компонента v z является постоянной в данном сечении канала. По отношению к рассматриваемой задаче из этого предположения следует, что решение уравнения (4) должно иметь вид

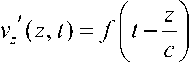
Здесь и далее величины, отмеченные одним штрихом, относятся к случаю, когда сечение вдоль канала не изменяется.

Формула (12) раскрывает физический смысл принятого предположения. Согласно этой формуле входное возмущение (10) распространяется вдоль канала со скоростью c , не меняя своей формы. Но это как раз тот тип течения, который соответствует течению крови в сосуде: в медицине такой тип течения носит название пульсовой волны.

Указанная аналогия открывает возможности для применения теории длинных волн при описании течения крови.

Сопоставляя выражения (12) и (10), приходим к выводу о справедливости равенства

^{ф (} t ) = f \ t

z

.

V c)

Подстановка формулы (12) в соотношение (6) и последующее интегрирование приводят к результату

vr

r d v^ 2 c d t

.

Подставляя выражение (14) в получаем

формулу (8) и выполняя интегрирование,

ur

r

• = Tv z ■ 2 c

Соответственно для давления получаем формулу

, a b , Р = —v, ■ 2 c ^z

Подставляя формулы (12) и (16) в уравнение (4), получаем

c =

"a b Y/2

V 2Р)

.

Теперь формулу (16) можно переписать в виде

p' = Р cvz' ■

По своему смыслу величина p' представляет собой разность систолического и диастолического давления, которую в гемодинамике принято называть пульсовым давлением.

Вышеприведенные формулы описывают поведение пульсовой волны при отсутствии катетера. Понятно, что введение последнего в сосуд изменяет картину течения. При этом катетер выступает в роли некоторого препятствия.

Согласно теории длинных гравитационных волн препятствие приводит к возникновению отраженной и прошедшей волн в дополнение к волне, падающей на препятствие. Сохраняя для характеристик падающей волны прежние обозначения v z и p', введем для аналогичных характеристик отраженной и прошедшей волн обозначения vz", p" и vz" ' , p"' .

В упомянутой теории при рассмотрении вопроса о течении жидкости в канале с препятствием оставляют в силе предположение о постоянстве компонент v_z , v_z , v_z"', а значит, и давлений p' , p'' , p"' (см. формулу (18)) по сечению канала. При этом условие непрерывности скорости для сечения z = 0, где располагается препятствие, записывается в виде

S - (v_z' - v_z") = s " v_z« ',

где S' и S" - площади сечения канала для z < 0 и z > 0, а условие непрерывности давления для того же сечения – в виде p + p = p ■

Учитывая формулу (18) и равенства S' = bb ² и S "" = п ( b ² - a 2 ), из системы уравнений (19)-(20) на участке канала z <  0 имеем

p = p' + p" = p'

1 -

a

2 b ²

Погрешность измерения пульсового давления

Формула (21), казалось бы, решает поставленную задачу: в этой формуле p" - это истинное давление, сумма p' + p" - давление p, измеряемое датчиком, а множитель

1 -

a

определяет систематическую погрешность измерения. Однако

2 b ²

этот вывод неверен. Сомнения в правомерности использования формулы (21) для расчета давления, измеряемого датчиком, порождает следующий факт.

Рассматривая картину линий тока (см. рис. 2), мы видим, что линия тока, совпадающая с осью симметрии, заканчивается в точке z = 0, r = 0 (ее принято называть в гидродинамике критической). В этой точке равна нулю не только нормальная к поверхности торца компонента vz , но и радиальная компонента vr . В силу последнего обстоятельства частицы жидкости, движущиеся по указанной траектории в направлении торца сплошного цилиндра, не могут обогнуть это препятствие, а отбрасываются от торца в обратном направлении вдоль оси симметрии. Для таких частиц складывается та же ситуация, что возникает при нормальном падении волны на абсолютно твердую бесконечную плоскость. Как известно, в последнем случае давление на этой плоскости равно давлению в падающей волне, умноженному на два. Следовательно, в рассматриваемом случае для критической точки имеем равенство p = 2 p".

Таким образом, оказывается известным значение функции p0 в точке r = 0, а именно

p 0 ^(0, t ) = ² p' ⁽ t )•

Как указано в работе [2], условия непрерывности скорости (19) и давления (20) выполняются, строго говоря, для пары сечений, удаленных от сечения z = 0 на расстояние порядка b . И если приближенно указанную пару сечений считать, следуя теории длинных гравитационных волн, совпадающей с сечением z = 0, то более логично (хотя это тоже некоторое приближение) говорить, что условие (20) выполняется не по всему сечению z = 0, а только на участке этого сечения r >  а , так как участок r <  а занят катетером.

Поскольку для давления должна соблюдаться непрерывность, из последнего соображения следует, что для граничного значения функции p0 можно записать выражение p 0(a,t) =

p '⁽ t ) •

1 -

2 b ²

Разложим функцию p ₀ ( r , t ) в ряд по степеням r , ограничившись членом второй степени. В силу осевой симметрии данной задачи справедливо равенство

5 p o ( r,t )
d r	r = 0

= 0, так что указанное разложение имеет вид po(r, t) = p'(t) ( 2 - Br2) .                                   (26)

Подставляя равенство (24) в формулу (26), определяем коэффициент B, получая для функции p0 (r, t) выражение p o( r, t) = p'(t) 2 - - 'ar2 .                         (27)

• ^ a 2 b — a J

Подставляя выражение (27) в формулу (11) и выполняя интегрирование, получаем

• , .      ,, . 3b — a

p. ( t ) = p ⁽ t )—_г ---г-                                ⁽²⁸⁾

2 b — a

Как видно из последней формулы, измеренное датчиком давление pт (t) отличается от истинного давления p 'tt), причем относительная систематическая pT — p ' погрешность £ = —т----составляет p'

^£ p

b ²

2 b — a

В качестве примера оценим погрешность, допускаемую при инвазивном измерении давления крови в аорте. Радиус аорты b примерно равен 1,5 см. Принимая для радиуса катетера a значение 1,5 мм, получаем ε p ~ 0,5.

Как следует из формулы (29), при больших значениях отношения a / b , что характерно для сосудов меньшего радиуса, чем аорта, погрешность превышает 50%.

Заключение

Как это уже указывалось, априори очевидно, что введение катетера в кровеносный сосуд меняет картину течения крови. Следовательно, манометр измеряет давление в потоке, возмущенном введением катетера. Диагноста же интересует давление в невозмущенном потоке, который реализуется при отсутствии катетера. Таким образом, уже изначально в метод инвазивного измерения закладывается погрешность. Здесь, по-видимому, важно подчеркнуть, что речь идет именно о погрешности метода – систематической погрешности. И естественным является вопрос, насколько велика эта погрешность.

Ответ, полученный в данной статье, несколько обескураживает: оказывается, эта погрешность превышает 50%.

Однако, как известно, то обстоятельство, что тот или иной метод характеризуется большой систематической погрешностью, вовсе не означает, что от этого метода следует отказаться. Если эта погрешность известна, то ее можно учесть, внося соответствующие поправки в измеренные указанным методом величины.

Главный результат данной статьи состоит в том, что в ней дан ответ на вопрос, как скорректировать измеренное значение давления крови, чтобы получить истинное значение последнего: для этого согласно формуле (28) необходимо измеренное

3 b ²

давление p _т разделить на величину _{2 b 2}

-

-

a

₂. Указанную операцию логично, по a ²

мнению авторов, назвать введением поправки на возмущение потока.