Возникновение флуктуаций амплитуды и фазы радиосигнала в турбулентной атмосфере

Случайные изменения параметров атмосферы оказывают существенное влияние на работу радиолиний [1]. Свойства радиолиний в тропосфере, стратосфере и ионосфере определяются многими параметрами: солнечной активностью, тепловыми режимами [2; 3], влажностью воздуха [4; 5], плотностью среды и т. д. Качественная передача радиосигнала является главной целью развития сетей связи в Российской Федерации [6]. Не последнюю роль в качественной передаче радиосигнала играют случайные турбулентные флуктуации воздуха.

В настоящей работе на основе модели взаимодействия детерминированного волнового процесса распространения передающей информационный сигнал радиоволны в турбулентной атмосфере и стохастического волнового процесса турбулентности атмосферы [7] рассмотрим флуктуации (или пульсации) амплитуды и фазы электромагнитной волны, влияющие на качество принимаемого радиосигнала. В радиофизике обычно используется термин «флуктуации», в теории турбулентности чаще используют термин «пульсации». В данной работе будем считать, что флуктуации параме-

тров радиоволн возникают за счет турбулентности атмосферы.

1.    Флуктуации эйконала электромагнитной волны

В [7] было использовано уравнение для электрического поля в электромагнитной волне в виде к 2 D = rotrot E ,                                       (1)

где D = (1 + 2 n ^) E - индукция электрического поля [7]; E - напряженность электрического поля, n / -турбулентные пульсации показателя преломления атмосферы; k – волновой вектор электромагнитной волны.

Подставляя в (1) величину D = (1 + 2 n / ) E и используя известную формулу векторного анализа, находим k 2 E + 2 к ² n / E «-A E + graddiv E . Пренебрегая вторым слагаемым в правой части в соответствии с уравнением div D = 0, имеем:

A E + к 2 E «- 2 к ² n^/ E .                               (2)

Для любых декартовых компонент Е вектора Е уравнение (2) можно записать в скалярном виде: A E + к ² E «- 2 к ² n^/ E .                               (3)

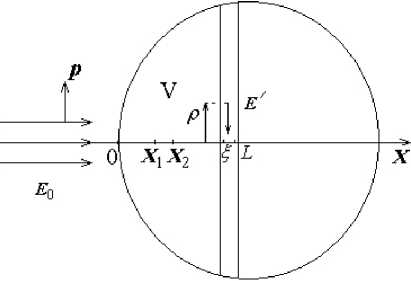
Аналогично [7] полагаем, что на некоторый условно выделенный объем V , рис. 1, в котором имеются турбулентные пульсации атмосферы, падает плоская электромагнитная волна с напряженностью электрического поля в волне:

E o = p A о e i ^kX , (4) где Х – координата распространения падающей волны; p – единичный вектор в плоскости колебаний вектора E o , перпендикулярный направлению распространения волны, т. е. волновому вектору k ; À ₀ – амплитуда волны; kX – фаза волны. Объем V лежит в области X >  0, а плоскость X = 0 является левой границей этого объема.

В результате воздействия турбулентных пульсаций в объеме V скалярные компоненты электрического поля в этом объеме можно записать в виде

E — AeiS — e ф, (5) где А – амплитуда электромагнитной волны; S – ее фаза, а ф — ln A + iS, (6) т. н. эйконал электромагнитной волны, который для падающей волны Eo имеет вид фo = ln Ao + iSo.

Флуктуации эйконала за счет турбулентных пульсаций можно найти по формуле ф1 — ф-Фo = lnI A- | + i(S-So) —х/ + iS*, (7) IAo )

где параметр х / = In ( A / A o ) характеризует флуктуации амплитуды, а величина S / = S - S o — флуктуации фазы электромагнитной волны за счет турбулентных пульсаций.

Учитывая Ф = Ф o +Ф / и, следовательно, E — = e ^{Ф o +ф} , из уравнения (2) получаем:

A^ o + Ф^ ) + V² ( ф o + ф^ ) + k ² = — 2 k^n . (8)

В соответствии с (4) эйконал падающей волны равен ф o = ln A o + ikX , следовательно, Vф o = ik и Aф o = o, поэтому уравнение (8) преобразуется к виду

Аф / + ( 2 ik + Vф ^/ ) Vф^/ = — 2 k ² n ¹. (9)

Уравнение (9) является нелинейным уравнением, но, учитывая малость турбулентных пульсаций эйконала ф / , можно предположить 2 ik » Vф ^/ и уравнение флуктуаций эйконала (9) записать в линейном виде:

Аф / + 2 ik Vф ^/ =— 2 k ² n / . (io)

dX

Рис. 1. Взаимодействие плоской электромагнитной волны в объеме V с флуктуациями волны Е /, возникающими за счет турбулентных пульсаций

Fig. 1. Interaction of a plane electromagnetic wave in volume V with wave fluctuations Е / arising due to turbulent pulsations

Применим уравнение (10) к конкретной геометрии, рис. 1. Направление вдоль координаты Х является выделенным, т. к. вдоль этого направления распространяется электромагнитная волна. Флуктуации эйконала ф / ( X ) по оси Х можно считать результатом наложения на электромагнитную волну рассеянных волн в слое dX объема V , рис. 1. Тогда уравнение (10) можно записать в виде

Аф / + 2 ik — = — 2 k ² n (11)

где

Аф ^/

д ² ф / + д ² ф / д Y ² д Z ²

Отбрасывая д ² ф / / д X ² , мы предположили, что основное влияние на электромагнитную волну оказывают рассеянные волны Е ^/ , лежащие внутри плоского слоя dX , рис. 1. На фронте плоской электромагнитной волны происходит частичное рассеяние этой волны на турбулентных флуктуациях. Рассеянные волны тут же складываются с волной, распространяющейся по оси Х . Это сложение происходит в узком слое dX на фронте волны.

Используя (7) и принимая n ^ = n 1 + in 2 , получим уравнения для действительной и мнимой частей ф¹ = х / + iS / :

Ах/ — 2k^— = —2k2n, дX

AS1 + 2 k — = —2 k2 n9, дx

где

Л    д2

A —--1

д Y ²   д Z¹

ках на оси Х в плоскостях ( Y . Z ) . модули которых вычисляются по формулам p = V Y ² + Z ² . рис. 1.

Подставив (19) и (20) в уравнение (18), имеем:

Исходя из системы уравнений (12) и (13), находя лапласиан А от левой и правой частей этих уравнений, получим отдельно уравнения для х ' и для S ' :

2 А 2 + 4 к 2 A_	х ' =	- 2 к 2	Г .      _ д n. ) А n + 2 к —2 .	(14)
V          д X 2 7			V 1      д X J
2 А 2 + 4 к 2	S1 =	- 2 к 2	д n 1 А n0 - 2 к —1 .	(15)
V          д X 2 ?			V 2      д X J

Г

J А ² + 4 к ²

2	Г            л2 Л А 2 + 4 к 2----	X	(21)
д X 1 2 J	V        д X 22 /

X e - ¹ k'^{P F} xx ( ^k'. ^X 1 . ^X 2 ) d ^k ' =

Будем считать турбулентные пульсации показателя преломления действительной величиной, так что n 2 = 0. Поэтому предыдущие уравнения

= J 4 к ⁴ А ² e - » F nn ( Z . X 1 . X 2 ) d Z .

Операторы, не зависящие от параметров интегрирования k ' и Z . вносим под знак

упростятся:

Г               ->2 ^

А ² + 4 к ²—- х' д X ²

' =- 2 к ² А n .

интегрирования.

Используя А ² e - i ^Zp = Z 4 e - i ^Zp в правой части (21) и А ² e - i ^{k p} = к ⁴ e - i ^{k p} в левой части, найдем:

Гл2 V

А2 + 4к2---- S' = 4к3—-.(17)

V        дX2 J

f к' 4 + 4 к 2 4

Ч       ^{д X} 1 ^j

V

V

к ⁴ + 4 к ²

д X 22 J

X

2. Двухточечные турбулентные корреляции

x e -'k ' ^{p F} xx ( ^k ' . ^X 1 . ^X 2 ) ^{d k} ' = = J ^{4 к 4} Z ⁴ e - i ^Zp F nn ( Z . X 1 . X 2 ) d Z .

Рассмотрим двухточечные корреляционные соотношения амплитудных пульсаций электромагнитной волны и турбулентных пульсаций показателя преломления атмосферы для двух точек X ₁ и X ₂ по оси Х , рис. 1. Для этого запишем уравнение (16) для точек X ₁ и X ₂ и перемножим эти

уравнения:

Г        Л2 Y

А ² + 4 к ^{2 д}

V       ^{д X} 12 Л

Л 2 ) А2 + 4 к2 д дX22 J

X

На данном этапе анализа необходимо задать физический закон влияния турбулентных пульсаций на электромагнитную волну. При дальнейших преобразованиях будем считать, что корреляции турбулентных пульсаций подобны корреляциям пульсаций параметров электромагнитной волны, которые возникают за счет турбулентных пульсаций. В частности:

B nn

^{ц В} XX .

^X (х ' ( X 1 ) х ' ( X 2 )} = ^{4 к 4 А} 2 n 1 1 ( X 1 ) n 1 ( X 2 )) .

т. е.

где угловые скобки, как обычно, означают про-

странственное осреднение.

Для решения уравнения (18) двухточечные корреляционные функции B nn = nn 1 ( X 1 ) n 1 ( X 2 )^ и B _XX = (х / ( X ₁ ) х ' ( X ₂ )^ с помощью Фурье-преобразования запишем через Фурье-спектры турбулентных флуктуаций F nn ( Z . X 1 . X 2 ) и флуктуаций амплитуды электромагнитной волны F „( k' . X „ X 2 ) :

B nn = J e ^{- Zp} F nn ( Z . ^X 1 . ^X 2 ) d Z . (19) B XX = J e - ‘ ^k'^{P F} xx ( ^k ' • ^X 1 . ^X 2 ) d ^k ' • (²⁰⁾ где k ' - волновой вектор электромагнитных флуктуаций; Z — волновой вектор турбулентных пульсаций; p - радиусы-векторы с началом в точ

J e - i ^Zp F nn ( Z . ^X 1 . ^X 2 ) d Z =

= p J e - i ^k ' ^p F _XX ( k ' . X ₁. X ₂ ) d k ' .

где ц - постоянный масштабный коэффициент

пропорциональности.

Используя (23), равенство (22) можно записать в

виде

J

^Гг к ! 1 2 V ^{2 к} j

V

д ²     Г к^{1 2}

+ дX 2 V 2 к /V

д ²

+-- дX2

/

X

X e ~^{1 k}'^{p F} xx ( ^k'. ^X 1 . ^X 2 ) ^{d k}' =

= 4 J Z ⁴ e ^- i ^k'^p F „„ ( к ' . X , . X 2 ) d k ' .

Приравнивая подынтегральные выражения, имеем:

^ff к ! ^{7 2}

V ^{2 к} 7

V

д ²

+-- дx 2

v

f к /2 7 2

V 2 к

V

7 д ²

+-- дX 2

² 7

х

«.« ) : «.R.. --':;-

^х Fxx

) = 4 Z ⁴ F nn ( ^к^ X 1 ’ X 2 ) .

. к ^/2 ( X 2 -^ ) х sin-----------

2 k

F nn ( ^к / ’ ^и ’ ^ ) ^{d и d} ^ ’

Решение уравнения (25) с начальным условием

F xx ( к / ’ О’ 0 ) = 0’ Рис. 1, найдем методом функции

Грина G :

^F xx ( ^к / ’ X 1 ’ X 2 ) =

X ₁ X ₂

= 4 Z ⁴ J J G ( к ’ к< X 1 ’ X 2 ’ и ^ ) F nn ( к / ’ и ’ ^ ) d и d ^ ’ 00

где X ₁ и X ₂ – координаты наблюдения двухточечных корреляций на оси Х , а и и ^ - координаты источника воздействия турбулентности на электромагнитную волну, рис. 1, с помощью т. н. функции влияния G ( к ’ к / ’ X 1 ’ X 2 ’ и ’ ^ ) .

Воспользуемся свойством 5 -функции Дирака:

Учитывая, что x и n - величины безразмерные, а F xx и F nn имеют одинаковую размерность, можно выбрать постоянную интегрирования В из условия B = 4.

Если на фронте волны X 1 = X 2 = L ’ рис. 1, то решение (31) приобретает вид

LL

^F xx^{( к}' ) =;< ⁴ JJ 00

. к ^/2 ( X 2 -^) х sin------------- J

2 k

к ^/2 ( X ₁ -и ) sin----------- х

2 k

F_nn ( к / ’ и>^ ) d и d ^ ’

F nn ( ^к X 1 ’ X 2 ) =

X ₁ X ₂

= J J ⁵ ( X 1 -и ) ⁵ ( X 2 -^ ) F nn ( ^к / ’ и ’ ^ ) d и d ^

где обозначено F (к/’ L’L ) = F (к/). Фактически xx             xx рассматривается единая точка по оси Х наблюдения воздействия турбулентных пульсаций на элек-

Подставив (26) и (27) в уравнение (25), найдем:

^{X 1} X ^{2 f}f k ^{/ 2} 7 ²

jj

V 2 ^к

V

+f- д x 2

V

f к ^/2 7 2

V 2 ^к

V

7 д дX2

² 7

х

х G ( к ’ к / ’ X ₁ ’ X 2 ’ и ’ ^ ) F nn ( к / ’ и ’ ^ ) d и d § =

X ₁ X ₂

= J J ⁵ ( X 1 -и ) ⁵ ( X 2 ^) F nn ( ^к / ’ и ’ ^ ) d и ^d ^

Из (28) получим вспомогательное уравнение

тромагнитную волну.

Для двухточечной корреляции B_ss = ^ S ( X 1 ) х х S ( X 2 )^ ’ характеризующей флуктуации фазы электромагнитной волны, в правой части уравнения (17) имеется производная д n 1 / д X . Поэтому в формуле (30) в точке X 1 = X 2 = L синусы для Фурье-спектра флуктуаций фазы заменяются на косинусы:

F SS ( ^к / ) = ;Z ⁴ J J cos ^к (к ^и) *                   (33)

к/2 (L-^)     ( , х х cos----2к----Fnn (к/’и’^)dиd^’

^ff к ! ^{7 2}

V ^{2 к} 7

V х G (к’ к

v

д ²

+-- дx 2

f к /2 7 2

V 2 к

V

. 7 д ²

+-- дX 2

х

’ и ’ § ) = 5 ( X 1 -и ) 5 ( X 2 -^ ) .

Если X 1 * и и X 2 * ^ т. е. вне точек воздействия и, следовательно, 5 ( X 1 -и ) 5 ( X 2 -£ ) = 0’ то частное решение уравнения (29) можно записать в виде

G ( к ’ к /’ X 1 ’ X 2 ’ U ’ ^ ) =

. ^{к /2} ( X 1 -и ) . ^{к /2} ( X 2 -^ ) = B sin  -------- s i n------------- ’

2 k 2 k

где В – постоянная интегрирования.

Таким образом, решение уравнения (25), согласно формуле (26), имеет вид

где также обозначено F ss (к^ L ’ L ) = F ss ( к / ) .

Кроме того, т. к. предположили X 1 = X 2 = L ’ логично также предположить единую координату источника воздействия турбулентности на электромагнитную волну с помощью функции влияния G , т. е. и = ^ . Следовательно, F nn ( к / ’ и, ^ 1 = = F nn ( ^к / ’ ^ ) .

Формулы (32) и (33) характеризуют связь турбулентных пульсаций показателя преломления атмосферы и флуктуаций амплитуды и фазы электромагнитной волны.

Проведем в (32) некоторые преобразования. Найдем интеграл по и :

/ X 4 2fc LL     к ^/2 ( L -? ) к ^/2 ( L -? )

F ( к ) = -;Z⁴-^ J J sin          d \ х (34)

^{xx               / 2}             2 к          2 к

k ^/2 ( L — 7 )

^{X sin} 2 k"^^F nn ( k ' , ⁷ ) d ^7-

X F nn ( ^k ' , 7 ) d 7 .

z ⁴ k L

= 2 ^Ц fc'2 ^J k ₀

^r . k ^{/ 2} ( L — 7 )        k ^{/ 2} L . k '2 ( L — 7 )"

s i n      — cos s i n    

2 k

2 k

2 k

X

Условие 7 ^ 0 (35) и (36) далее:

позволяет упростить формулы

X F nn ( ^k ' , 7 ) d 7^{- 2} Ц^ 7 Г J k ₀

. ^{k /2 ( L —7) sin}     2 k

—

^ zz ( ^k '      - 4 L ¹

—

—

V

V

• k ^/2 _r sin — L

k к '2 kL

k

L

J F nn ( ^k ' , 7 ) d 7 ,

1 r

—

. k ^/27, . ^{k / 2} ( ^{2 L} — 7 ) sin-- + sin------------

2 k

V

2 k

F nn ( ^k ' , 7 ) d 7 .

F ss ( ^k ' ) -4 ^{L 1}

Учитывая, что L близко к 7 , но не равно 7 , можно заменить

. k -^/2 ( L — 7) k ^/2 ( L — 7) sin----------- ®----------

2 k

2 k

.

Полагаем, что основное воздействие на электромагнитную волну осуществляется сразу после ее поступления в турбулентную область объема V , рис. 1. Поэтому используем условие 7 ^ 0, следовательно,

sin---- ®---- и cos---- ® 1.

2 k 2 k        2 k

Таким образом, формула (34) преобразуется к виду

F XX

(k') = 2^ J k0

z ⁴ k J Г k /2 ( L — 7 )

2 k

V

—

1 r

k /27    . k ^/2 ( 2 l — 7 )

—    + sin

2 k

2 k

_ z⁴ k L Г k ^/2z_{r и}

^{-ц J} T ( ^{L —7)}

V

₊ k ^/27 2 k

F nn ( k ' , 7 ) d 7 =

—

• k sin— L +

k

k ^/27

+ cos

2 k

k

. /2 1

--L F

k

nn

( k ' , 7 ) d 7-

r L

= ц7 ⁴ L J

—

• k \ sin — L k k± L k

—

k

./2 1

— 1 — cos-— L

2 L

k

X

X F nn ( k^Z, 7 ) d 7 .

Аналогично для для Фурье-спектра флуктуаций фазы из (33) найдем:

F SS ( ^k ' ) = r

L

-.-* L J

V

• k ^/2_r sin— L

k kl L

k

—

k

1 . /2 1

— 3 + cos-- L

2 L

k

X

• k ^/2 _r sin — L

k к '2 kL

k

Анализ, проведенный сделать вывод, что

L

J F nn ( k ' , 7 ) d 7-П F nn ( ^k ' ) .

Следовательно:

L

J F nn ( ^k7 d 7

в [8], дает возможность

F _zz ( k ' ) -лцZ ⁴ L

F ss ( k ' ) = ^Л^^ 4 L

Г	k / 2	1
	sin —	L
1 —	k
	k12 т
	L
V	k	7
Г	. k /2	1
	sin —	L
1 +	k
	k /2 r
	L
V	k	7

F nn ( k ' ) .

F nn ( k ' ) ,

_k '2

Если — L « 1, то, разлагая в ряд Тейлора k

. k/2 r    k/2 r sin L« L —

k

k

получим:

Г k ^/2 1 3 L ³

k

6,

F _zz ( k ' ) -лцZ ⁴ L 1

/ nn

— nu L

—

/2 k_L

k

kl L k

—

3 Г k '2 1 2

k

F SS ( ^k ' )-^z^{4 L 1}

1 k ^/2 1 3 L ^{3 1}

k

z ⁴ F nn ( k ' ) ,

⁺ fc'2 k_L

V k

X

7 к '2 —L

k

—

^r k^{12 1 3} k

L 3 ^

X

X F nn ( ^k ' ) = ²^L z ⁴ F nn ( ^k ' ) .

Таким образом, Фурье-спектр флуктуаций

ам-

плитуды электромагнитной волны пропорциона-

лен кубу расстояния, пройденного волной в турбулентной среде, четвертой степени волнового числа флуктуаций волны и обратно пропорционален квадрату волнового числа волны. Фурье-спектр флуктуаций фазы электромагнитной волны пропорционален первой степени пройденного волной расстояния. Зависимость флуктуационных параметров электромагнитной волны от волнового числа турбулентности будет уточнена ниже.

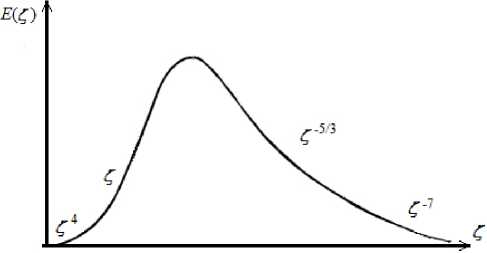
Рис. 2. Спектр турбулентности. Зависимость энергии турбулентности от волнового числа турбулентных пульсаций

Fig. 2. Spectrum of turbulence. Dependence of the turbulence energy on the wave number of turbulent pulsations

3. Влияние энергетического спектра турбулентности на радиосигнал

Чем более короткие электромагнитные волны используются для радиосигнала, тем большее влияние на них оказывает турбулентность. Это логично, т. к. при более коротких волнах их размер приближается к размеру турбулентных флуктуаций,

Z

J F ( Z ) d Z = - 2 a

^Л ® 3

)    3

J E ² ( ^Z ) d^Z 3 ^Z 2 ,

l z

что искажает сигнал.

В формулы (41) и (42) входит спектральная функция пульсаций волнового числа электромагнитной волны: F nn ( k / ) ~ F ( Z ) • Заметим, что первоначально, формула (19), в спектральной функции F_nn использовалась зависимость от волнового числа

турбулентности. Предполагаем, что волновые числа турбулентных пульсаций подобны флуктуациям волнового числа электромагнитной волны Z ~ к / , которые возникают за счет турбулентных пульсаций.

Определение спектральной функции турбулентных пульсаций представляет довольно сложную

и неоднозначную задачу. Прежде всего заметим, что пульсации показателя преломления n / определяются пульсациями давления воздуха p / = р и ^2 [9], где р - средняя плотность воздуха, и ^2 ~ E -

квадрат пульсаций продольной скорости возду-

ха, пропорциональный энергии турбулентности [9]. Следовательно, B nn = ^ n 1 ( X 1 ) n 1 ( X 2 )^ ~ E ( Z ) • Связь между функцией F ( Z ) и E ( Z ) исследовалась многими известными учеными: Гейзенбергом [10], Карманом [11], Коважным [12], Обуховым [9]. Эти ученые предлагали различные формулы

связи. Стюарт и Таунсенд [13] показали, что функ-

Z ция JF (z) dZ представляет собой произведение 0

двух сомножителей, первый - интеграл от Z до » ,

второй - интеграл от 0 до Z , безотносительно точной формулы этих сомножителей.

Для изотропной турбулентности мы ограничимся относительно простой формулой Коважного:

где a - постоянная величина.

В спектре турбулентности, рис. 2, при увеличении волнового числа турбулентности Z размер турбулентных вихрей уменьшается. На максимуме спектра турбулентности находится область т. н. энергосодержащих турбулентных вихрей. Далее по спектру турбулентных волновых чисел Z , т. е. более мелких вихрей, находится т. н. инерционная область спектра. Для энергии турбулентности в инерционной области спектра турбулентности, рис. 2, примем формулу, полученную независимо друг от друга Колмогоровым [14], Онзагером [15], Вейцзекером [16]:

- 5

E ( Z ) = C Z ³ ,                                         (44)

где С – величина, не зависящая от волнового числа турбулентности Z .

Инерционная область волновых чисел характеризуется тем, что турбулентность в этой области находится в статистическом равновесии: поток энергии от более крупных турбулентных вихрей к более мелким определяется вязкой диссипацией самых мелких вихрей. Эти самые мелкие вихри лежат уже за пределами инерционной области – в области, описываемой законом Гейзенберга ~ Z - 7 • Вязкая диссипация турбулентных вихрей в самой инерционной области незначительна. Турбулентность в инерционной области не зависит от внешних условий.

Если подставить (44) в (43), то получаем Z

J F ( z ) d Z = const, и, следовательно, F ( Z ) = 0, что, 0

естественно, не отражает общих свойств спектра для любых волновых чисел турбулентности.

В качестве более полного описания спектральной функции турбулентности по сравнению с (44) используем результат, полученный Коважным:

5 (

E ( Z ) = C 1 Z ^{3 1} -n i Z I

4 f 3

,

где C i и n — величины, не зависящие числа турбулентных пульсаций.

Подставляя (45) в (43), найдем:

от волнового

z

J F ( Z ) d Z = - 2 a

( » 3       1

J E ^{2 (Z)} d ^z 3 z ² =

l z

Г да

= - 2 a J C 1 Z ²

5 (

4 ^ ³ 1

z

² 1 - 2 n i Z ³ d Z 3 Z ²

®

( ®

5 (

4 I

)     3

-т

- 2 a J C i Z ² 1 - 6 n i Z ³ d Z з Z ² =

l Z I

(/ X 3

- 2 a C 1

3 Iz^{- 2} - 36 n 1 Z

= -^a C 1 + 48 a C 1 n 1 Z ³ •

Следовательно:

F ( Z ) « 64 a C 1 n 1 Z ³ •

Делаем вывод, что в

1 1     3

6 2 Z ² =

(41) и (42) зависимость

от волнового числа турбулентности имеет вид 1     13

4+—   —

Z ³ = Z ³ • Детальное сравнение четырех различных спектральных формул для энергии турбулентности проведено в книге [17]. Обращает на себя внимание достаточно сильное влияние на электромагнитную волну турбулентной атмосферы, до более чем четвертой степени волнового числа турбулентности.

Заключение

На основе модели взаимодействия детерминированного волнового процесса распространения электромагнитных волн в атмосфере и случайного волнового процесса турбулентных пульсаций атмосферы исследовано возникновение флуктуаций эйконала электромагнитной волны, зависящего от амплитуды и фазы волны и влияющего на качество передаваемого радиосигнала. Влияние

турбулентных пульсаций давления в атмосфере приводит к пульсациям показателя преломления, которые в свою очередь приводят к пульсациям параметров электромагнитной волны, в частности к пульсациям эйконала.

Полученное дифференциальное уравнение для флуктуаций эйконала распадается на два взаимосвязанных уравнения. Первое уравнение – для флуктуаций амплитуды, второе уравнение – для флуктуаций фазы.

Найдены дифференциальные уравнения для двухточечных турбулентных корреляций показателя преломления, параметров, зависящих от флуктуаций амплитуды и флуктуаций фазы.

С использованием Фурье-преобразования методом функции Грина показано подробное решение дифференциального уравнения для параметра, связанного с двухточечной корреляцией турбулентных флуктуаций амплитуды электромагнитной волны. Представлено также решение уравнения для параметра, связанного с двухточечной корреляцией турбулентных флуктуаций фазы электромагнитной волны. При этом использовалось физическое предположение о подобии двухточечных корреляций турбулентных пульсаций и двухточечных корреляций флуктуаций параметров электромагнитной волны, которые возникают за счет турбулентных пульсаций.

Показано, что Фурье-спектр двухточечной корреляции пульсаций амплитуды электромагнитной волны пропорционален кубу расстояния, пройденного волной в турбулентной среде, четвертой степени волнового числа флуктуаций волны и обратно пропорционален квадрату волнового числа волны. Фурье-спектр двухточечной корреляции флуктуаций фазы электромагнитной волны пропорционален первой степени пройденного волной расстояния.

На основе проведенного анализа, а также использования спектра энергии турбулентности найдено, что зависимость Фурье-спектров двухточечных корреляций турбулентных пульсаций амплитуды и фазы электромагнитной волны пропорциональна волновому числу турбулентности в степени тринадцать третьих.

Сделан вывод о достаточно сильном влиянии турбулентной атмосферы на качество передающих сигнал радиоволн.