Возникновение и нелинейные режимы конвекции трехкомпонентной смеси в прямоугольной области пористой среды с учетом эффекта Соре

Большинство жидкостей и газов, встречающихся в природных и технологических процессах, являются многокомпонентными. Сложный состав смеси учитывают при изучении коллоидных смесей [1, 2], выращивании кристаллов [3, 4], распространении загрязняющих примесей в водных объектах [5, 6], мембранных процессах [7], в задачах фильтрации [8–11], добычи углеводородов [12, 13]. Наличие нескольких механизмов переноса тепла и массы в смесях значительно усложняет их изучение [14–17]. В современных исследованиях в качестве моделей многокомпонентных смесей часто рассматриваются трехкомпонентные углеводородные жидкие смеси. Примером такой трехкомпонентной смеси может служить смесь додекана, изобутилбензола и тетралина, которая активно изучалась ранее и была использована в качестве рабочей среды в экспериментах по определению коэффициентов диффузии

и термодиффузии DCMIX-1, проведенных на Международной космической станции [18, 19]. Компоненты этой смеси являются представителями основных групп химических соединений, входящих в состав нефти.

Смесь додекана, изобутилбензола и тетралина, взятых в равных пропорциях при температуре 25°С, характеризуется положительными значениями отношений разделения компонент, то есть легкие компоненты этой смеси под действием градиента температуры накапливаются в более нагретой области [20, 21]. Для характерного в природных условиях геотермального градиента температуры (нагрев снизу) это означает, что тяжелая компонента смеси накапливается в более холодной части области (сверху), что приводит к неустойчивости системы.

В работе [22] для бинарной смеси, заполняющей горизонтальный слой пористой среды, найдены границы монотонной и колебательной неустойчивости в зависимости от значений отношения разделения и пористости среды. Для случая колебательной неустойчивости показано, что при уменьшении пористости среды устойчивость течения повышается.

В работе [23] изучались возникновение и нелинейные режимы термоконцентрационной конвекции смеси додекана, изобутилбензола и тетралина в квадратной области пористой среды с твердыми непроницаемыми границами при нагреве снизу и теплоизолированых вертикальных границах. Показано, что в разных условиях могут формироваться 1- и 2-вихревой стационарные режимы. Последний при увеличении числа Релея сменяется стационарным течением, имеющим несимметричную 2-вихревую структуру. Одновихревое стационарное течение при увеличении числа Релея сменяется режимом стационарных колебаний. Дальнейший рост числа Релея приводит к нерегулярным колебаниям. Расчеты проведены при разных значениях пористости среды; найдено, что при небольшой пористости возможно существование двух разных колебательных режимов: с малой и большой амплитудами колебаний.

Настоящая работа является продолжением исследований, представленных в [23]. Описываются результаты численного моделирования возникновения и нелинейных режимов конвекции смеси додекана, изобутилбензола и тетралина, взятых в равных долях, в вытянутой в горизонтальном направлении прямоугольной области пористой среды с твердыми непроницаемыми для вещества границами при нагреве снизу. Расчеты проведены для того же значения пористости (0,1), при котором в [23] найдено наибольшее число режимов. Данная конфигурация моделирует месторождение углеводородов.

2.    Постановка задачи

Если смесь состоит из n компонент и концентрации первых i = 1,..., n - 1 компонент составляют C i , n -1

тогда концентрация n -й компоненты равна C_n = 1 - ^ C i . Для описания состава смеси достаточно указать i =1

вектор концентраций (массовых долей) C = ( C 1 ,..., C n ,) . Последнюю компоненту — компоненту с номером n , будем называть растворителем, а первые n -1 — примесями. Рассмотрим термоконцентрационную конвекцию в пористой прямоугольной полости со сторонами L и H ( L = 5 H ), заполненной однородной трехкомпонентной жидкой смесью. Плотность смеси линейно зависит от температуры T и концентраций составляющих ее компонент C i , где i = 1,..., n - 1:

Р = Р с (1 -в T (T - T 0 ) - 1 ■ B ( C - C 0 )).

Здесь:

_   1 др=-

Р 0 ^{д T} с

коэффициент теплового расширения; B = diag{ e i , ^ , в _n -1} — диагональная

матрица коэффициентов концентрационного расширения (такая, что в _C

1 др

ρ∂ C

^{0         1} T , C j , J =1, ■■■, n -1, J # i

i = 1,..., n - 1); I = (1, ...,1); C — вектор концентраций; р ₀, C ₀ = ( C ₁₀,..., C n _ _1>0) и T ₀ — начальные плотность, вектор концентраций и температура смеси.

Нестационарные уравнения свободной термоконцентрационной конвекции смеси в пористой среде в рамках модели Дарси-Буссинеска с учетом эффекта термодиффузии имеют вид [24]:

0 = - ± vp-VV - g (в T (T - T) +1 ■ B (C - с 0)), р0 K

( р c уд Т + ( р c ) f V ■v T = xV T ,

е ^ + V -V C = D V 2 C + C 0 ( I - C 0 ) D T V 2 T ,                        (3)

V- V = 0.                                                     (4)

Здесь: V — скорость фильтрации; p — давление; g — ускорение свободного падения; t — время; K — проницаемость; v — кинематическая вязкость; X * — эффективная теплопроводность пористой среды; ( р c ) — эффективная теплоемкость пористой среды; ( р c ) — теплоемкость жидкости; е* — пористость; D — матрица коэффициентов молекулярной диффузии смеси; D _T — вектор коэффициентов термодиффузии. Уравнения записаны в предположении постоянства вязкости и коэффициентов переноса в пренебрежении эффектами бародиффузии и Дюфора. Задача решается при следующих граничных условиях: предполагается, что полость имеет твердые непроницаемые для вещества границы, при этом боковые — теплоизолированы, на горизонтальных — поддерживаются разные постоянные температуры, соответствующие нагреву снизу.

Приводя матрицу коэффициентов молекулярной диффузии в исходных уравнениях к диагональнму виду, можно исключить перекрестные диффузионные эффекты и тем самым уменьшить число определяющих параметров задачи. Результат этого преобразования в размерных переменных запишется как [25]

C = MQ ^{- 1} C ,     D T = MQ ^{- 1} D _T ,                              (5)

где M — матрица, в столбцах которой находятся собственные векторы m i = ( m i 1 ,..., m in -1 ) ^T матрицы D ;

n -1

^Q = diag { q _p..., q n -1 } , q_t = P -1 ^ P m .

j =i

Преобразование (5) позволяет привести размерные уравнения (1)–(4) к системе с диагональной матрицей D ^ˆ , вектором концентрации C ^ˆ и вектором коэффициентов термодиффузии D ^ˆ _T :

0 = - Vp-V v - g (pT (T - To)+1 - B ( C - C)),(6)

Po     K                     \»

(pc)*dT + (pc) V -VT = X*V2T,(7)

d t f

ˆ

E*dC + V-V C = D V2 C + C0 (I - C0) DT V2 T,(8)

V- V = 0.(9)

Выберем в качестве единиц измерения следующие: длины — высоту полости H ; скорости — aH , где a = X *Др c ) _f — эффективная температуропроводность; времени — H ² ( p c ) /x* ; давления — p₀ a v/ K ;

отклонения температуры от равновесного значения — AT ; отклонения концентрации от равновесного значения

( ? 0 ( C - 1 ) A t i > t (ID)

Преобразованные уравнения (6)–(9) в безразмерной форме

принимают вид:

0 = -Vp - V + Ra (T + y<(2) k ,(10)

^T + v-V T = V2 T,(11)

d t

E^C + V-V <7 = Le-1 (v2 <7 -1V2 T),(12)

V-V = 0.(13)

Здесь: Ra = KgPTH AT (^av) — аналог числа Релея для пористой среды, который в дальнейшем для краткости будем называть «числом Релея»;

4 ^ = - < 7 0 ( I - ( 7 0 ) p T *B ( ID ) - 1 J D t

вектор отношений

*

разделения, характеризующий термодиффузионные свойства смеси; о = о (рc)f /(рc) — нормализованная пористость; Le = a (D)

-J

— диагональная матрица чисел Льюиса такая, что Le 11 = a J1D11 , Le 22 = a) 1X2 ;

k — единичный вертикальный вектор. Для безразмерных переменных сохраним прежние обозначения.

На всех границах поставим условия непроницаемости, отсутствия диффузионного потока компонентов, на горизонтальных границах зададим температуру, на вертикальных — отсутствие потока тепла:

Ограничиваясь рассмотрением двумерных течений, введем функцию тока как

v =dl

x

8у

y      d x ■

x = 0,5:     V x = 0,   d- g x	d C	0,	(14)
	= 0,         = оx
у = 0: V = 0,     - = 1,	8 C - I dT_	= 0,	(15)
y у = 1: V = 0, T = 0,	d у    d у d C - I dT_	= 0.	(16)
y	d у    d у

Уравнения (10)–(13) и граничные условия (14)–(16), записанные в терминах функции тока, принимают вид:

х ш D ( 9 T ■< C ) V 2 ¥ = Ra — +1 /  , ^ d x     d x J		(17)
d T + g^ d T g^ d T = v T 8 1 8 y g x 8 x 8 у       ’		(18)
8 ( 2 8^8 ( 2 8^8 ( 2 T -1/^2-	I V 2 T ) ;	(19)
о i                                .i^e i V C 8 1    8 у 8 x    8 x 8 у
ˆ x = 0,5: Y = 0, — = 0, — = g x       8 x	0,	(20)
у = 0: ^= 0, T = 1, i C -1 5 -	= 0,	(21)
у = 1: ^ = 0, T = 0, iC -1 ^	= 0.	(22)

Задача (17)–(22) решалась численно, методом конечных разностей. Пространственные производные аппроксимировались центральными разностями. Нестационарные уравнения приводились к дискретному виду с помощью явной конечно-разностной схемы с постоянным временным шагом, равным h ² 16, где h — шаг по пространству. Уравнение Пуассона для функции тока разрешалось методом последовательной верхней релаксации. Этот алгоритм применялся при исследовании возникновения и нелинейных режимов конвекции трехкомпонентной смеси в квадратной полости с твердыми границами в работах [26, 27].

Рассмотрим подробно начальные условия. Температура и концентрации обеих компонент в момент времени t = 0 считались линейно зависящими от вертикальной координаты (подогрев снизу), а для функции тока использовалась многовихревая структура с малым числовым коэффициентом:

t = 0: Т = 10 ⁸ sin ^—J sin (^л У ) , T = 1 - у ,    C 1 = C 2 = 1 - у .

Для прямоугольной полости с соотношением сторон 5:1 значения длины волны начальных возмущений l принимались равными 10 или 2, что давало 1- или 5-вихревое слабое течение. Однако, как показали дальнейшие расчеты, значение l не влияет на формирующееся течение, если начальное возмущение имеет вид (23).

Параметры рассматриваемой трехкомпонентной смеси додекана, изобутилбензола и тетралина, взятых в равных долях при температуре 25°С, представлены в Табл. [18, 21].

Таблица. Параметры смеси додекана, изобутилбензола и тетралина

Параметр смеси	Значение	Параметр смеси	Значение
Р о ( кг/м 3 )	843,5	dm ( м 2 /с )	6,70	10 - 10
в т ( 1K )	0,914 - 10 — 3	D 12 ( м 2 /с )	0,43 -	10 - 10
в С ,	0,258	D 21 ( м 2 /с )	- 1,08	10 - 10
в с 2	0,121	D 22 ( м2/с )	11,10	10 - 10
v ( м2 /с )	1,528 - 10 — 6	D T ( м2/ ( с к ) )	- 0,81	10 - 12
a ( м2 /с )	10 - 7	D T ( м2/ ( с к ) )	- 0,93	- 10 - 12

Применяя преобразование (5), приводящее матрицу коэффициентов молекулярной диффузии к диагональному виду, получаем следующие значения безразмерных параметров: ^ = 0,341, xj^ = 0,109, Le = 1,47 - 10 2 , Le₂ = 0,91 - 10 2 .

Расчеты проводились для чисел Релея в интервале от 0 до 30. Пористость среды в расчетах принималась равной 0,1 (характерна для таких сред как песок, песчаник, известняк [28, 29]).

3.    Численные результаты

Для обсуждаемой в настоящей работе трехкомпонентной смеси додекана, изобутилбензола и тетралина оба отношения разделения примесей положительны (см. выше определение вектора отношений разделения и Табл.), поэтому при подогреве снизу более легкие компоненты смеси додекан и изобутилбензол вследствие термодиффузии накапливаются возле нагретой нижней границы полости, а тяжелая компонента смеси — тетралин, вблизи холодной верхней границы. Это создает дополнительную неустойчивую стратификацию по плотности, связанную с неоднородностью концентрации, вызванной неизотермичностью, и понижает порог возникновения конвекции, которому в однокомпонентной жидкости при вертикальном градиенте температуры отвечает Ra₁ = 4 л ², если в течении формируется один вихрь, и Ra₂ = 25 п ² /4 при образовании двух вихрей, расположенных рядом [8]. В случае бинарной смеси порог определяется выражением Ra = Ra₁ Д1 + v ( 1 + Le ) ) для 1-вихревого движения и Ra = Ra₂ Д1 + ^ ( 1 + Le ) ) для 2-вихревого движения [8].

На рисунке 1 а показана вычисленная зависимость числа Нуссельта от числа Релея в диапазоне значений Ra = 0,0 - 14,0. Число Нуссельта представлялось как тепловой поток через нижнюю границу полости на единицу ее длины:

Nu =

1 iTL dx .

L L d x

Шаг по числу Релея в основных расчетах принимался равным 1, однако при выявлении перехода к другому режиму шаг уменьшался вплоть до 0,05 (для более точного установления границы существования режима).

Конвекция возбуждается мягко при Ra ® 0,25 (см. Рис. 1 а , кривая 1 ). Структура возникающего течения вблизи порога конвекции является 1-вихревой и сохраняется до значения Ra ® 3,0. При Ra ® 0,4 формируется 2-вихревой режим (Рис. 1 а , кривая 2 ). При превышении числом Релея значения Ra ® 3,0 для 1-вихревого течения и значения Ra ® 1,5 для 2-вихревого вблизи боковых границ полости образуются дополнительные вихри, смещающие оба течения в центральную часть полости. В диапазоне чисел Релея Ra ® 4,0 - 12,5 существуют многовихревые стационарные режимы со структурой течения, имеющей несколько вихрей разного размера (Рис. 1 а , кривые 3-5 ). При Ra ® 10,25 - 12,5 существует несимметричный стационарный режим (Рис. 1 а , кривая 6 ). В диапазоне чисел Релея, который приведен на рисунке 1 а , обнаруживаются также два колебательных режима (см. кривые 7 и 8 ). На рисунке 1 б представлена структура установившегося течения для каждого из найденных режимов. При дальнейшем увеличении числа Релея колебательные режимы переходят в нерегулярные колебания. Момент смены режима регулярных колебаний на нерегулярные определялся по виду кривых временной эволюции локальных и интегральных характеристик течения: функции тока, температуры и концентрации компонент в некоторой точке, по максимальному значению модуля функции тока в полости, числу Нуссельта.

а

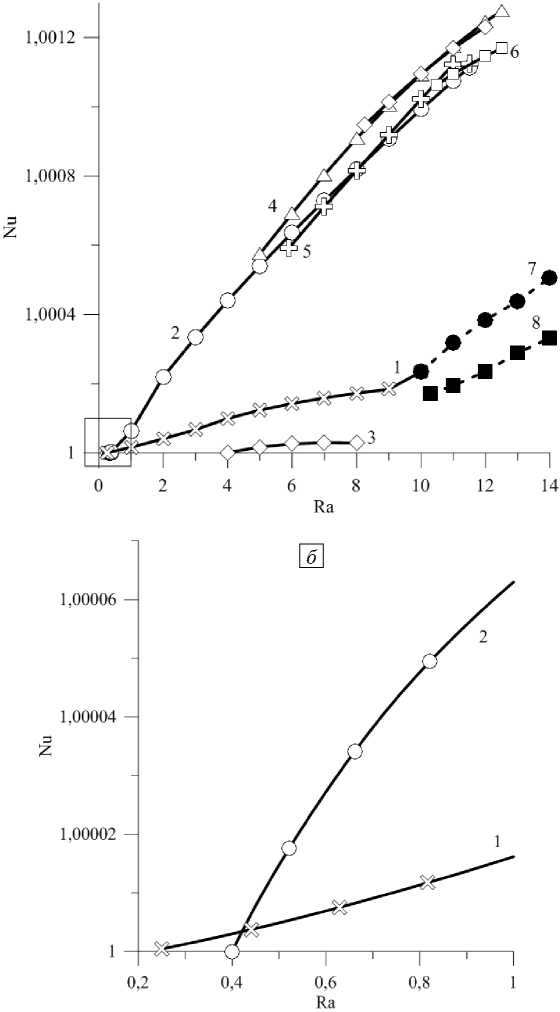
Рис. 1. Зависимость числа Нуссельта от числа Релея для разных режимов течения ( а ), их начальный участок в увеличенном масштабе ( б ) (кривые 1 – 6 отвечают стационарным движениям, кривые 7 и 8 – колебательным движениям; для колебательных режимов по вертикальной оси отмечено среднее значение числа Нуссельта за период колебаний в установившемся течении) и соответствующие режимам поля функции тока ( в ) (указаны максимальные значения функции тока Т _ж и интервала между изолиниями ЛТ ; светлые/темные участки соотносятся с большим/меньшим значением функции тока)

в

Режим 1

Ra <  3,0 , Т m = 0,002 , ЛТ = 0,006

Ra <  1,5 , Т _m = 0,022 , ЛТ = 0,0044

Ra >  1,5, Т _m = 0,055 , ЛТ = 0,011

Режим 3.

Ra <  8,25, Т _m = 0,055, ЛТ = 0,011

Ra >  8,25 , Т _m = 0,09 , ЛТ = 0,018

Режим 4.

Т _m = 0,045, ЛТ = 0,09

Режим 5.

Т _m = 0,05 , ЛТ = 0,01

Режим 6.

Т _m = 0,055 , ЛТ = 0,014

Режим 7.

Т _m = 0,05 , ЛТ = 0,014

Режим 8.

Т _m = 0,09 , ЛТ = 0,018

• 3.1.    Стационарные конвективные движения

Рассмотрим подробнее результаты расчетов. Одновихревое стационарное движение, соответствующее кривой 1 на рисунке 1 а , получено с использованием в качестве начальных условий установившихся стационарных полей функции тока, температуры и концентраций компонент смеси, вычисленных для близкого по величине большего значения числа Релея. Этот режим наблюдается при Ra ® 0,25 - 9,0.

На рисунке 2 представлена временная эволюция разности концентраций 1-й компоненты смеси — A C 1 , в центрах верхней и нижней границ полости и распределение концентрации 1-й компоненты смеси при Ra = 2,0 и Ra = 4,0. В первом случае реализуется одновихревое движение, занимающее весь объем полости, во втором появляются дополнительные боковые вихри, смещающие основной вихрь к центру. Начальными состояниями в этих расчетах выступали решения при Ra = 3,0 и Ra = 5,0 соответственно. Временная эволюция и распределения концентрации для 2-й компоненты смеси, которая имеет отношение разделения смеси того же знака, качественно выглядят аналогично, поэтому они здесь и далее не приводятся. Как видно из рисунка 2 а , с ростом числа Релея в полости очень быстро устанавливается новое течение с большей интенсивностью.

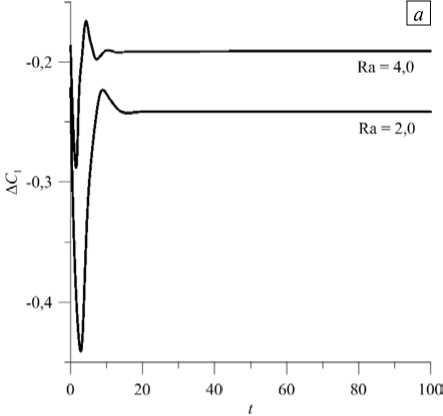
Рис. 2. Временная эволюция для режима 1 (Рис. 1 а , кривая 1 ) разности концентраций 1-й компоненты смеси в центрах верхней и нижней границ полости ( а ) и установившееся распределение концентрации 1-й компоненты ( б ) (светлые/темные участки соответствуют большему/меньшему значению)

б

Ra = 2,0

Ra = 4,0

Стационарное 2-вихревое движение (Рис. 1 а , кривая 2 ) было обнаружено в интервале Ra ® 0,4 - 3,0 при использовании в качестве начальных условий выражений (23), в остальном диапазоне существования этого режима (до Ra ® 11,5) начальными условиями служили установившиеся стационарные поля функции тока, температуры и концентраций компонент смеси, рассчитанные при близком по величине (большем/меньшем) значении числа Релея. На рисунках 3 а , б представлены временные эволюции максимального значения модуля функции тока в полости — |^| m ( t ) , и разности концентрации

1-й компоненты смеси — A C 1 ( t ) , соответственно, в центрах верхней и нижней границ полости

0.05

а

О

б

0,04

-0.2 -

0,03

е

В*

0,02

0,01

Ra = 2,0

Ra - 0.5

-0.4

<

-0,6

-0,8

Ra = 2,0

Ra - 0.5

• 0 Г 1 I 1 I 1 I 1 I 1 I                                        -I I11 I ']-----------।-----------1-----------1-----------1-----------1-----------1-----------।1

О 100     200     300     400     50С                 0 юо 200     300     400500

1t

Рис. 3. Временная эволюция максимального значения модуля функции тока в полости ( а ) и разности концентраций 1-й компоненты смеси в центрах верхней и нижней границ полости ( б ); изолинии функции тока с указанием максимального значения функции тока и интервала между изолиниями ( в ) и распределения концентрации ( г ) на различных этапах формирования течения (светлые/темные участки соответствуют большему/меньшему значению функции тока или концентрации в случае реализации режима, соответствующего кривой 2 на рисунке 1 а )

г

в

Функция тока                        t = 20

T m = 0,0065, AT = 0,0013

t = 50

T m = 0,02 , AT = 0,004

t = 100

T m = 0,022 , AT = 0,0044

t = 400

T _m = 0,022 , AT = 0,0044

Концентрация 1-й компоненты

t = 500

T _m = 0,022 , AT = 0,0044

Рис. 3. Продолжение

при значениях числа Релея 0,5, 1,0 и 2,0 в случае реализации 2-вихревого течения. Течение в полости возникает в некоторый момент времени t ^* , величина которого уменьшается с ростом числа Релея [30–32], и имеет 6-вихревую структуру, затем количество вихрей уменьшается до двух (Рис. 3 в ). Изменения пространственного масштаба течения происходят скачком. Распределение концентрации 1-й компоненты смеси на каждом этапе развития течения содержится на рисунке 3 г . Этот режим наблюдается при Ra ® 0,4 - 11,0.

Режимы 3–5 (см. отвечающие им кривые 3–5 на Рис. 1а) характеризуются многовихревой (от шести до десяти вихрей) структурой течения. В некотором интервале своего существования эти режимы были вычислены с использованием в качестве начальных возмущений выражений (23). Так, 6-вихревая структура монотонного течения (режим 3) была получена при начальных условиях (23), Ra ® 4,0 - 4,8 и Ra ® 8,25 -11,0, 8-вихревая (режим 4) — при Ra ® 5,0 - 6,0, а симметричная 10-вихревая (режим 5) — при Ra ® 6,25 - 8,1. Для режима 3 найдено, что при Ra ® 8,25 меняется направление вращения вихрей (Рис. 1а, кривая 3), что сопровождается скачком значения числа Нуссельта. Для других режимов смена направления вращения вихрей при принимаемых во внимание значениях параметров и условиях не обнаружена. Установившееся распределение концентрации 3-5 представлено на рисунке 4 при расчете с Ra = 7,0.

В зависимости от начальных условий в интервале значений реализация четырех стационарных конвективных движений (Рис.

1-й компоненты смеси для режимов числа Релея Ra ® 6,0 - 9,0 возможна 1а, кривые 1–4). Рисунок 5 содержит

зависимость кинетической энергии течения Ek = jp(V2/2)dS (здесь S — площадь полости) от волнового S числа k реализуемого течения при фиксированном значении числа Релея. Волновое число определялось по среднему значению длины волны вихревой структуры течения. Максимальная интенсивность течения наблюдается при к « 3,77 , что соответствует 6-вихревому течению режима 3.

Вследствие эффекта термодиффузии в полости происходит разделение компонент смеси, однако конвективное течение, перемешивая жидкость, препятствует этому процессу [14, 18, 24–25]. Со временем разность концентраций между верхней и нижней границами достигает постоянного значения — A С ^, и его абсолютная величина тем меньше, чем больше интенсивность течения. На рисунке 6 а приведена зависимость A С 1 ^ст от числа Релея в интервале существования монотонных режимов 1-5. Как видно,

а

б

в

Рис. 4. Установившееся распределение концентрации 1-й компоненты смеси при Ra = 7,0 для различных стационарных режимов: режим 3 ( а ), режим 4 ( б ), режим 5 ( в )

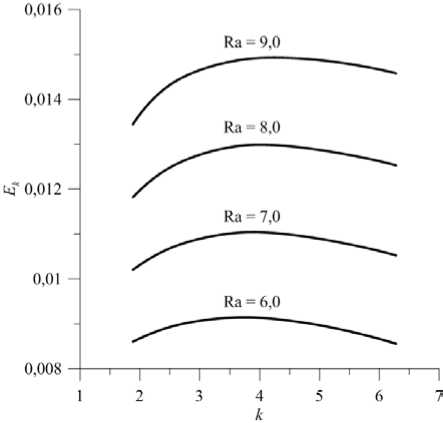
Рис. 5. Зависимость кинетической энергии движения в прямоугольной полости от волнового числа реализуемой структуры стационарного движения при различных значениях числа Релея

максимальное значение А С ₁ ^ст ®- 0,2 достигается при реализации режима 1 при Ra ® 4,0. В области существования режимов 2-5 разность А С ₁^ст стремится к значению -0,2, но не достигает его из-за большей интенсивности течения.

При числе Релея, равном 12,0 , использование начальных условий (23) приводит к возникновению несимметричного стационарного движения (Рис.1 а , кривая 6 ). В этом случае течение имеет 10-вихревую структуру, в которой 2-й справа вихрь занимает большую часть полости, чем другие вихри. С ростом значения числа Релея этот вихрь увеличивается в размере, а остальные вихри сужаются и сдвигаются в левую часть полости, зависимость А С ₁ ^ст ( Ra ) приобретает немонотонный характер (Рис. 6 б) . Установившиеся распределения концентрации 1-й компоненты смеси в начале и в конце интервала существования этого режима представлены на рисунке 6 в .

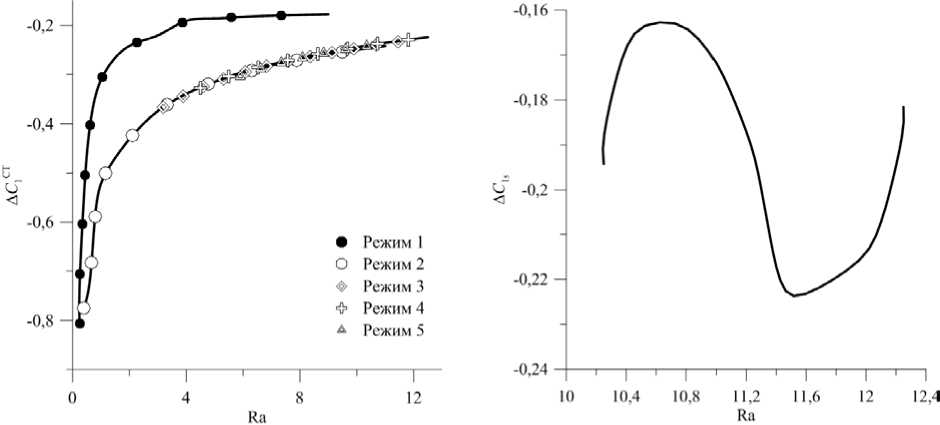
Ra = 10,25                     Q                      Ra = 12,5

Рис. 6. Зависимость установившегося значения А С 1 от числа Релея при реализации: монотонных режимов 1-5 ( а ); несимметричного стационарного движения 6 ( б ); установившиеся распределения концентрации 1-й компоненты смеси в начале и в конце интервала существования режима 6 ( в )

• 3.2.    Колебательные режимы

Увеличение числа Релея при реализации любого стационарного движения приводит к возникновению колебательных режимов (Рис. 1, кривые 7 и 8 ). При росте Ra режим 1 (1-вихревой с боковыми вихрями возле вертикальных стенок полости) и многовихревые режимы 3–6 сменяются колебательным режимом 7, имеющим 1-вихревую форму с боковыми пристеночными вихрями. В случае режимов 3–6 при переходе происходит перестройка структуры течения, присутствует скачок зависимости теплового потока через нижнюю границу полости от числа Релея. Переход от стационарного режима 2 с 2-вихревой структурой течения и парой вихрей возле вертикальных границ к колебательному режиму 8 с 2-вихревой структурой течения также сопровождается перестройкой структуры течения, и, кроме этого, наблюдается скачок зависимости Nu(Ra) .

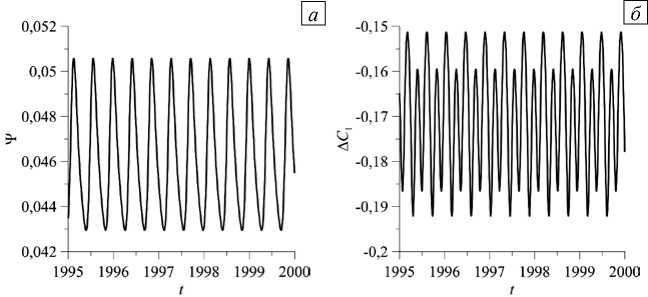
Рис. 7. Временная эволюция функции 1-й компоненты смеси в центрах верхней для режима 7 при Ra = 12,0

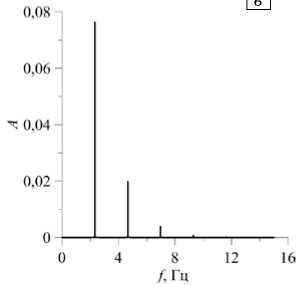
тока в точке с координатами ( 0,25; 0,525 ) ( а ), разности концентраций и нижней границ полости ( б ) и спектр Фурье колебаний функции тока ( в )

Колебательный режим 7 был получен с использованием начальных условий (23) при Ra ® 12,25 - 12,5 .

Остальная часть кривой 7 на рисунке 1 отвечает решениям с начальными возмущениями полей функции тока, температуры и концентрации компонент, рассчитанных при меньших/больших значениях числа Релея. Минимальное значение Ra , при котором появляются колебания, равно ~10,0. Кривые временной эволюции функции тока в точке с координатами ( 0,25; 0,525 ) и разности концентраций A C 1 между границами за несколько периодов установившихся колебаний представлены на рисунке 7 а , б при Ra = 12,0. Для других значений числа Релея форма колебаний функции тока и разности концентраций качественно остается той же. Основная частота периодических колебаний функции тока в точке ( 0,25; 0,525 ) для Ra = 12,0 равна f 1 ® 2,32 Гц. В спектре Фурье (Рис. 7 в ), соответствующем этим колебаниям, с частотой f ₁ соотносится самый большой первый пик амплитуды A . Остальные пики спектра показывают частоты, кратные основной частоте. С увеличением числа Релея эта частота возрастает.

а                                  б                              в

Ra = 11,0

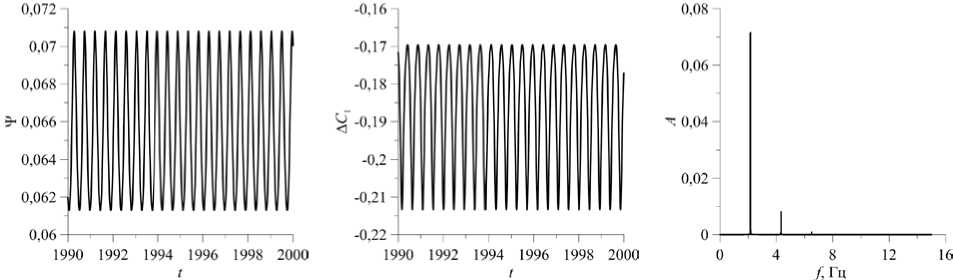
Рис. 8. Временная эволюция функции тока в точке с координатами ( 0,25; 0,525 ) ( а ) и разности концентраций 1-й компоненты смеси в центрах верхней и нижней границ ( б) , а также спектры Фурье колебаний функции тока ( в ) для режима 8 при разных значениях числа Релея

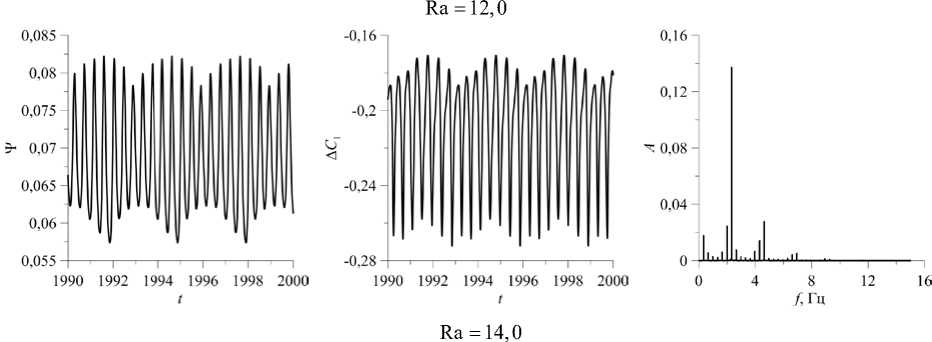
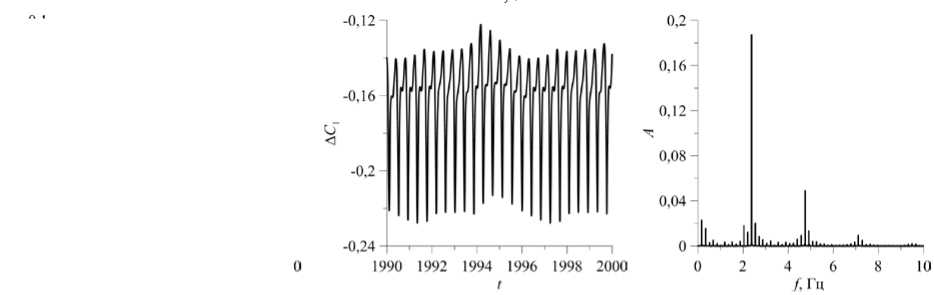
Рис. 8. Продолжение

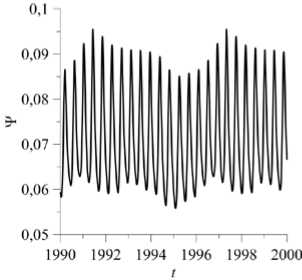
При числе Релея Ra = 13,0 и использовании в качестве начальных условий состояния (23) в полости наблюдается колебательный режим с течением, имеющим 2-вихревую форму (Рис. 1, кривая 8 ). Этот же режим при начальных возмущениях полей функции тока, температуры и концентрации компонент, полученных для меньшего/большего значения числа Релея, может реализоваться, начиная с Ra ® 10,3. С ростом числа Релея вдоль кривой 8 на рисунке 1 следует усложнение формы колебаний функции тока в точке ( 0,25; 0,525 ) и разности концентраций A C 1 (Рис. 8 а , б) . Для Ra = 11,0 колебания функции тока в точке ( 0,25; 0,525 ) , как и для режима 7, остаются периодическими с основной частотой f1 ® 2,17 Гц (см. высокий пик в спектре Фурье на Рис. 8 в , при Ra = 11,0). Фазовые траектории, изображенные на плоскости локальных значений функции тока ¥ и температуры T (в точке ( 0,25; 0,525 ) ), представляют собой цикл (Рис. 9, Ra = 11,0). При Ra = 12,0 (Рис. 8) колебания становятся квазипериодическими,

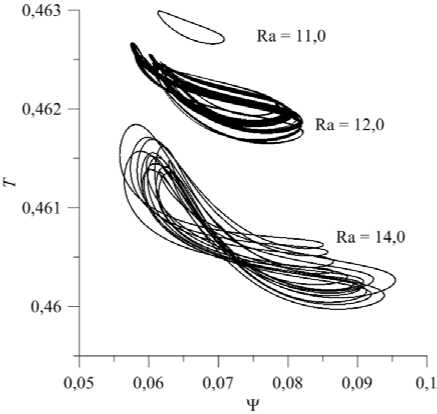
Рис. 9. Фазовые траектории колебаний, представленных на Рис. 8 а , при различных значениях числа Релея

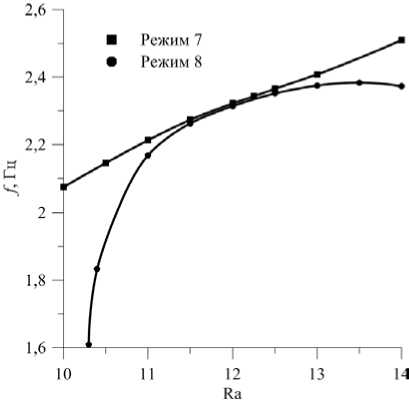
Рис. 10. Зависимость от числа Релея частоты самого высокого пика спектра Фурье для колебаний функции тока в точке ( 0,25;0,525 )

появляется вторая частота. На спектре Фурье для этих колебаний первой основной частоте f 1 а 0,33 Гц соответствует первый видимый пик, второй частоте f 2 а 2,36 Гц — самый высокий пик. Остальные частоты на спектре являются комбинацией этих двух основных частот.

Можно предположить, что механизм возникновения квазипериодических колебаний заключается во взаимодействии процессов диффузии и термодиффузии трехкомпонентной смеси. Фазовый портрет этих колебаний, показанный на рисунке 9 при Ra = 12,0, имеет вид двумерного тора. Дальнейший рост числа Релея приводит к удвоению периода колебаний, так что f 1 а 0,17 Гц (Рис. 8, Ra = 14,0, первый пик в спектре Фурье), при этом значение частоты, соответствующей самому высокому пику спектра, равно f 2 а 2,32 Гц. Фазовый портрет этих колебаний изображен на рисунке 9. Бифуркация удвоения периода колебаний является механизмом перехода к нерегулярным колебаниям.

Рисунок 10 содержит зависимость от числа Релея частоты, соответствующей самому высокому пику в спектре Фурье, 1- и 2-вихревого колебательных режимов. Видно, что для 1-вихревого колебательного режима эта зависимость близка к линейной, в то время как для 2-вихревого колебательного режима зависимость немонотонная, с максимумом при Ra = 13,5. При этом значении числа Релея появляется удвоение периода колебаний.

4.    Заключение

Численно исследованы возникновение и нелинейные режимы конвекции трехкомпонентной смеси додекана, изобутилбензола и тетралина в вытянутой в горизонтальном направлении прямоугольной полости пористой среды при подогреве снизу. Параметры пористой среды, характерные размеры полости и разности температур выбраны близкими к реальным параметрам пород в условиях нефтяных и газовых месторождений. Компоненты рассматриваемой смеси, взятые в равных долях, обладают положительными отношениями разделения, поэтому под действием термодиффузии легкие компоненты (додекан и изобутилбензол) накапливаются в нагретой нижней части полости, а тяжелый — тетралин, возле верхней холодной границы. Это вызывает конвекцию. Представленные результаты показывают, что при Ra >  0,25 в полости возможна реализация нескольких стационарных конвективных движений, имеющих одно- или многовихревую структуру течения и отличающихся пространственным масштабом. Обнаружен стационарный режим с несимметричной структурой течения. С ростом числа Релея происходит переход к колебательным режимам. В исследованном интервале чисел Релея (Ra = 0,0 - 14,0) найдено два колебательных режима со сложной формой колебаний мгновенных характеристик течения. Реализация конкретного режима зависит от структуры и интенсивности течения, используемого в качестве начальных условий.

Исследования выполнены при финансовой поддержке правительства Пермского края (Программа поддержки научных школ Пермского края, Соглашение № С-26/788).