Временная эволюция фазовой плотности ансамбля ионов, удерживаемого ловушкой Пауля

В работе получены аналитические выражения, описывающие динамику фазовой плотности ансамбля ионов, удерживаемого цилиндрической гиперболической ловушкой (Paul trap).

Ловушка Пауля (Paul trap) [1] позволяет управлять устойчивостью движения ионов, удерживаемых внутри электродной системы. Тот факт, что уравнения движения зависят от массы, позволяет использовать ловушку как масс-спектрометр. В большинстве исследований, посвященных динамике ионов в ловушках, рассматривается поведение одиночного иона [1, 2], в то время как коллективная динамика исследуется численно [3]. В работе [4] предложен метод импульсного воздействия на ионное облако (de pulse tomography), открывающий перспективы сверхвысокого разрешения для масс-спектрометров типа «ионная ловушка». В основе метода лежат два факта: 1) колебания ионов с близкими массовыми числами и одинаковыми начальными условиями рано или поздно окажутся в противофазе; 2) подача короткого импульса, синхронизированного с управляющим напряжением, оказывает тормозящее действие на одну группу ионов и ускоряющее на другую, которая покидает ловушку и детектируется.

Поскольку на время удержания ионов в ловушке нет принципиальных ограничений, то всегда можно дождаться, когда колебания окажутся в противофазе и, таким образом, получить сколь угодно высокую разрешающую способность.

В связи с тем, что для реализации метода импульсного воздействия необходимо знать не только координату, но и скорость иона, представляет интерес исследовать динамику функции распределения ансамбля ионов на стадии удержания в объеме ловушки.

Движение одиночного иона в цилиндрической гиперболической ловушке описывается уравнениями Матье, как для радиальной Кл\ так и для вертикальной Дг) компонент движения [I]. Поскольку уравнения имеют одинаковый вид, достаточно рассмотреть одно из них, например z + (a- 2qcos(2t))z = 0, где параметры a, q связаны с питающим напряжением и массой иона, t — безразмерное время [1]. Фундаментальная система решений уравнения Матье может быть записана в виде [5]

z(7) = A(z0, z., ЙК (Л + B(z0, z^, z)/2 (Г), где (zn, zn,Z) — начальные условия, а функции Матье Cev, Sevдля краткости обозначены как fvfY Выразим начальные условия (z0, zn, Z) в виде

„ _т М (7) - Л (tu (D) - д/, (z)/₂ (D - /₂ <М (Л) "°       дтт-дтлт ’

_{д ;} дЛ (0Z СП - Д (ЩП) - z(j₂ иц. m -/; (оЛ СО)

Выражения (1) устанавливают взаимно однозначное соответствие между точками (z₀, z_n, Z) и (z, z,Т), лежащими на интегральной кривой, а координаты (z₀,z_Q) представляют собой переменные Лагранжа, для которых введем обозначения z₀ = F_x (z, z, t, T), z₀ = F₂ (z, z,t,T).

Пусть за интервал времени dt в фазовом объеме ^/р ₌ dzdz образовалось s^z, z, t^dTdt ионов, где 5 — скорость образования ионов в интервале фазовых координат z-.-Z + dz, z---z ⁺ dz.

Поскольку в расширенном фазовом пространстве интегральные траектории не пересекаются, то попасть в интервал JT частицы могут только из предыдущих состояний, находящихся на данной интегральной кривой. Тогда, зафиксировав переменные (z,f , 7), можно записать закон сохранения числа частиц пЦЕ\ Юг (t),t)dT(t) - п(РА V - dt), F2 (t-dt),t- dt)dT(t - dt) =s(F^t),F2 (/), t)dT(t)dt-          (2)

Поскольку для рассматриваемой гамильтоновой системы фазовый объем сохраняется в силу теоремы Лиувилля, то, сокращая на Г и расписывая второй член в левой части по степеням dt, получаем неоднородное уравнение Лиувилля вида

Эп dF. дп dF, бп ,           ,.      . . .                 й» Ли

⁺ —T^ + -7- ^{+ o}(dF₁,dF,,dt)--5(z,2,0 _или    2 + —z + —=-$(г,2Д).

cP dt dF, dt dt                           ’ dz dz Qt

С другой стороны, сократив (2) на dT и разделив на dt, получаем — = -8(Р^),Р_г(1),1), откуда, интегрируя по времени от 0 до Ги считая, что в начальный момент времени система не содержит частиц п(0) = 0, получаем

т

n(z, z,T) = p(F| (2,2, т, Т), F,_tz, s, т, Г), ^di, о

Таким образом, показано, что интеграл (3) удовлетворяет неоднородному уравнению Лиувилля и, значит, задает одночастичную функцию распределения (нормированную на полное число частиц). Для вычисления интеграла (3) необходимо определить скорость образования ионов s в фазовом пространстве.

Рассмотрим рождение иона как стационарный случайный процесс, который характеризуется независимыми случайными величинами: случайной координатой ^ случайной величиной проекции скорости д₀ на ось Z и случайным моментом времени t, в который произошло образование иона.

Образование ионов происходит в результате процесса электронно-ударной диссоциации, при этом пучок ионизирующих электронов параллелен оси Z. Если концентрация ионизируемых молекул пт остается неизменной во время периода ионизации Tv то движение каждого электрона можно рассматривать как независимое испытание, тогда вероятность образования заданного числа ионов Nion (или рассеянных электронов N) определяется биноминальным распределением, среднее значение которого имеет вид (dNil>n) = -(dN^ = N^n^z^, где а — эффективное сечение ионизации, тогда —— - -Ncanm и ^N^z^ = (A^ (0))exp(- cnmz0), где (АДО)) — среднее число электронов, эмитируемых катодом. Полученное соотношение аналогично закону Бугера — Ламберта — Бера, описывающему поглощение света в среде.

Введем в описание число Кнудсена, равное отношению характерного размера системы к средней длине свободного пробега молекулы к„ = bjbi_ma_kin, где b — длина интервала пучка электронов, на котором производится ионизация, a_kin — газокинетическое сечение молекулы. Среднее число ионов, образовавшихся на интервале 0...^, имеет вид

(AU-)) = (A,(0)) 1 -exj

, где предположено, что эффективное сечение ионизации при близительно совпадает с газокинетическим сечением молекулы. В случае К « 1, который практически всегда выполняется для масс-спектрометрических устройств [6], воспользуемся приближением ехр(е) = 1 + е, откуда        =            =            где / — ток пучка b е о          с электронов, е — элементарный заряд. Плотность вероятности, соответствующая описанному распределению ионов в пространстве и времени, имеет вид a>_(z0,/) = (£)“' Т^'.

Распределение ионов по скоростям определяется квантовым механизмом неупругового взаимодействия электрона и молекулы. Ссылаясь на экспериментальные данные, можно сказать, что при электронно-ударном механизме диссоциации направления векторов скоростей осколочных ионов распределены изотропно [6], а разброс энергий осколочных ионов не превышает несколько электрон-вольт [7] (например, для иона 4ПСа+, ^EE[^ 1,3 эВ [8]), что на порядок меньше энергии управляемого движения, то есть для плотности вероятности, описывающей распределение ионов по скоростям, можно записать ®4(i0) = 8(-0).

В силу независимости описанных процессов плотность вероятности co(zo, z0, /0) = (67}) 15(z0), откуда, пользуясь частотным определением вероятности, получаем скорость заполнения фазовых состояний

s(z.,z0)=^^Sy<,) = C,6U.>                  (4)

о е V2

Вычислим интеграл (3), подставляя (1) в (4) и пользуясь известным из теории функций Матье соотношением f_x ^^ - /, (z)/₂ (z) = X = ^const t⁵!’ ^полУч^аем

n(z, z, Z) =    J§[z(/2 (Zo )/, (z) - /, (Zo)/2 (Z))— z(/2 (Zo)/] (Z) - /t (Zo )/2 (Z))}/Zo.

A о

Делая замену переменных для аргумента дельта-функции и интегрируя

n(z, Z, ) = — У —тт-----------— ----Д—----:  --------:----V где tk, удовлетворяющие условию 0 < tk < 7}, определяются из уравнения

^тА_к )/i(7}) - Д U_кМт ^У Ут(t_kМх^) - /,Ц_кMMJi )) = 0-

Поскольку все производные записаны для безразмерного времени Z, полученные соотношения могут быть переписаны в полярной системе координат посредством преобразования - = 7cos

Приравнивая значения фазовой плотности, выраженные в разных системах координат, получаем M(z, z)r/z<7z = n(7 cos(cp), J sin(

п а у^лУмдачУЗКУг^               ’     <5>

Как следует из (6), время образования иона Zk полностью определяет угловую координату Ф и фазовую плотность n(

На рисунке 1 показана зависимость угловой координаты ф от времени рождения иона t_k, рассчитанная по формуле (6).

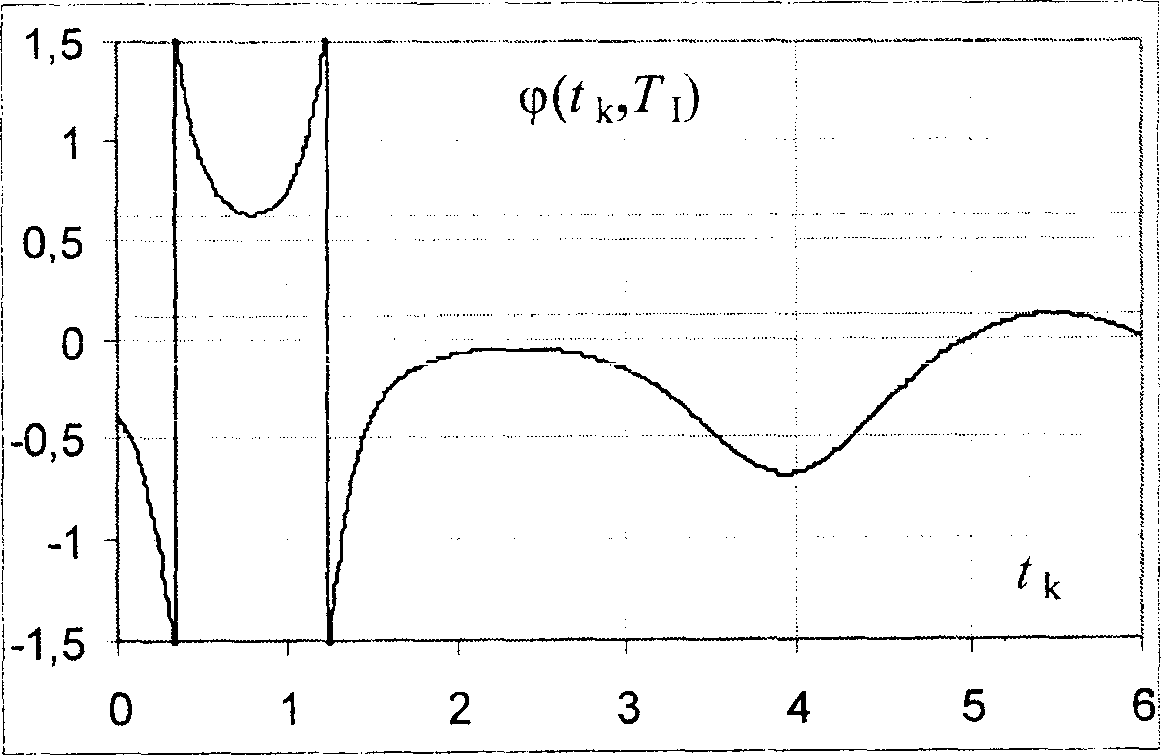
Рис. 1. Зависимость угловой координаты ф>от времени рождения иона t_k

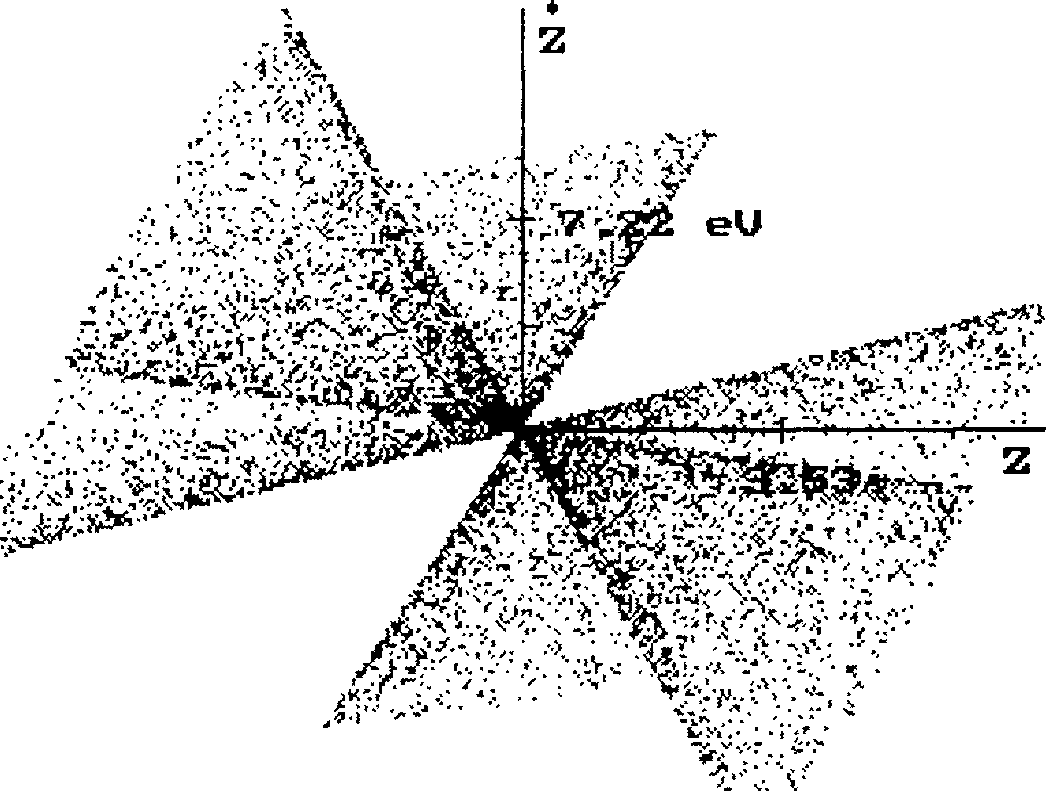
Рис. 2. Фазовый ансамбль ионов, полученный в результате численного моделирования

Для проверки полученных формул (5), (6) было произведено численное решение уравнения движения, начальные условия которого соответствовали (4) при параметрах: С] = 9000/6 (за 6 единиц безразмерного времени образовалось 9000 ионов, равномерно распределенных на интервале 0 < z₀<  b, 0 <  t < Т,), а = 0, q = 0,23413. Результат расчета показан на рисунке 2.

Полученные формулы описывают эволюцию фазовой плотности ансамбля ионов и могут быть использованы как для численных расчетов, так и для дальнейших аналитических исследований. Преимущество описания динамики ионов на языке функции распределения состоит в том, что, определив процесс дестабилизации, можно получить регистрируемый прибором сигнал, чего нельзя сделать, исследуя поведение одиночного иона.