Временная зависимость амплитуды объектной волны при четырехволновом взаимодействии с учетом резонансной и тепловой нелинейностей

1. Модель среды

Соответствие между комплексными амплитудами падающей (сигнальной) и преобразованной (объектной) волн является важнейшей характеристикой любого четырехволнового преобразователя излучения. Знание такого соответствия позволяет решить вопрос о целесообразности применения четырехволновых преобразователей в системах нелинейной адаптивной оптики, в системах обработки и преобразования изображения и т. д. [1–3].

Как правило, изучение соответствия между комплексными амплитудами сигнальной и объектной волн при четырехволновом взаимодействии происходит на нелинейности одного типа. Учет нескольких типов нелинейности существенно усложняет решение поставленной задачи.

При четырехволновом взаимодействии в поглощающих средах, например в средах с резонансной нелинейностью, существенный вклад в объектную волну может быть обусловлен наличием тепловой нелинейности [4–9]. Поэтому представляет интерес изучение пространственновременного соответствия между комплексными амплитудами сигнальной и объектной волн при четырехволновом взаимодействии с учетом как резонансной, так и тепловой нелинейностей.

Рассмотрим нелинейную среду, состоящую из непоглощающего растворителя и поглощающего растворенного вещества. В качестве поглощающего вещества возьмем ансамбль частиц, моделируемый двухуровневой схемой энергетических уровней. При распространении излучения наличие резонансной нелинейности приводит к изменению коэффициента поглощения, а наличие тепловой нелинейности – к изменению по- казателя преломления.

Пусть в нелинейной среде навстречу друг другу распространяются две волны накачки с комплексными амплитудами A ₁, A ₂ и сигнальная волна с амплитудой A ₃. В результате вырожденного четырехволнового взаимодействия to + to - to = to генерируется объектная волна с комплексной амплитудой A ₄ , распространяющаяся навстречу сигнальной волне.

Исходное скалярное волновое уравнение, описывающее четырехволновое взаимодействие, есть

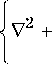
k ²11 + A dn ( n ₀ dT

Здесь

5 T ^- 2 ik а > ( A + A *) = 0. (1)

A = E A j , j = 1

a — коэффициент поглощения; 5 Т — изменение температуры, обусловленное выделением тепла при поглощении излучения; k — to n о / с , n о -среднее значение показателя преломления.

Для поглощающих частиц, моделируемых двухуровневой схемой энергетических уровней, коэффициент поглощения связан с заселенностью основного энергетического уровня соотношением вида a = N1^12 - N2^21 = N1 (^12 + ^21) - N^21, (2) где N1 и N2 – заселенности основного и возбужденного уровней; N — N + N — общая концентрация частиц; стij - сечение перехода между i и j энергетическими уровнями.

Уравнение (1) дополняется нестационарным уравнением теплопроводности

— — _ZV²5 Т + — I . (3) d t C p v

V² + k ² f1 + — — 5 T 1- 2 ik a, (    n _о dT

m — 1 ^ 3;

V² + k ² 11 + — dn 5 T o I - 2 ik a₀ ^    n о dT )

+

2 k ² dn n о dT

5 T 31

)

2 ik a₃₁ A 2 — о.

и кинетическим уравнением, описывающим из-

менение заселенности основного энергетическо-

го уровня,

——¹ = ^- N i I CT 12 + N 2 ⁽ I CT 21 + ⁵ 2i ) . dt

Здесь I — AA * ; 5 21 - вероятность безызлучатель-

ного переходов между возбужденным и основ-

ным энергетическими уровнями; c _p – теплоем-

кость; x — температуропроводность; v — плот-

ность вещества.

2. Вывод выражений, связывающих временные зависимости пространственных спектров взаимодействующих волн

В приближении заданного поля по первой волне накачки при учете решетки, возникающей при интерференции первой волны накачки и сигнальной волны, распределение интенсивности можно записать следующим образом:

I — I о + ( A 1 A 3 + A ? A 3 ) ,                          (5)

где 1 0 = A 1 A ^; .

С учетом (5) коэффициент поглощения, изменение температуры среды можно представить в виде суммы быстро (а з1 , 5 T 31 ) и медленно (a o , 5 Т о ) меняющихся в зависимости от поперечных координат составляющих:

a ( r, t ) = а о ( r , t ) + а з1 ( r, t ) ,

5 T ( ? , t ) = 5 Т _о ( ? , t ) + 5 T ₃₁ ( r , t ) .

Волновое уравнение (1) распадается на систему уравнений вида

A m = о,

A 4 +

Пусть волны накачки плоские:

^A 1,2 ( ^r ) ^— A 1,2 ( z ) exP ( ^{- ik} 1,2 r ) .

Сигнальную и объектную волны разложим по плоским волнам

да

A j ( r, t ) — J AA j ( к j , z , t ) exp ( - i к j p - ik jz z ) d к j ,

-да

j — 3,4

Здесь A _j – пространственный спектр j -й волны; к j и k jz — поперечная и продольная составляющие волнового вектора k j ; r ( p, z ) — радиус-вектор.

Быстро меняющиеся составляющие температуры и коэффициента поглощения разложим по

гармоническим решеткам:

да

5 T 31 ( r, t ) — J

^a 31 ( r, t )

5 T 31 ( к t , z , t ) exp ( - i к t P ) d к t ,

-да

да

J a 31 ( к с , z , t ) exp ( - i к с p ) d к с

-да

где 5 T 31 и (i 31 — пространственные спектры тепловой решетки и решетки коэффициента по-

глощения.

В приближении медленно меняющихся ам-

плитуд с учетом разложения взаимодействующих волн по плоским волнам, а быстро изменяющихся составляющих температуры и коэффи-

циента поглощения – по гармоническим решеткам от системы уравнений (6) можно перейти к следующей системе уравнений:

dA_m    k [ ik dn        )

—m +         5 T + a A — о, dz   kmz (nо dT о о J m ,

m — 1 ^ 3;

dA 4     k 1 ik dn

+I dz   k4 z ( nо dT

^{5 Т} о ^{+ a} 0

^*

A 4 +

k k 4 z

ik dn n ₀ dT

⁵ ^ T 31 ^{+ a} 31

^*

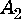
X

X exp [- iz ( k 2z - k 4 z ) ] — о.

Система уравнений (8) получена при условии к т = к c = K i - к з = -к 2 + к 4 . Эту систему уравнений необходимо дополнить граничными условиями:

нением (4) при замене в нем N _l на N _{l 0} и I на I ₀, а другое имеет вид

A 1 ( z = 0, t ) = A 10 ( t ) ,    A 2 ( z = t , t ) = A 20 ( t ) ,

/-V dN

,.  = - N111 0^12 + N 21 (I 0^21 + 521) + dt

A 3 ( к з , z = 0, t ) = A 30 ( к з , t ) , A 4 ( к 4 , z = t , t ) = 0.

Решение первых трех уравнений системы (8)

⁺ F ( t , ^к 1 N , ^z ) .

есть

A 1 ( ^z , t ) = AV 10 ( t ) exp ( - C i ( ^z , t ) ) ,

A2 (z, t) = A20 (t) exp (-C2 (z, t) + C2 (t, t)),(9)

A3 (к3, z, t) = A30 (к3, t) exp (-C3 (z, t)), где

^C j ( ^z , t ) = V" f f k dn ⁵ T 0 ( ^z 1 , t ) ^{+ a} 0 ( ^z 1 ) l d^z 1 .

kjz 0 I n0 dTJ

Сделаем замену A 4 ( z , t ) = A 4 ( z , t ) exp(- C 4 ( z , t )).

Тогда с учетом (9) при квазиколлинеарной геометрии взаимодействия (k/k13z ® 1, ^/^24z ® -1) уравнение, описывающее изменение пространственного спектра объектной волны, примет вид dA‘ (к4, z, t)

dz

Здесь

-               x            1             -

F ^(к 1 N , ^z , t ) = ^- 2 I 31 ^(к 1 N , ^z , t ⁾⁽ N 10 ^CT 12 ^{- N} 20 ^g 21 ) ,

I 31 ^(к 1 N , ^z , t ) = ^A 10 ⁽ t ) " A 30 ^(к 3 , t ) ^x

X exp |^- iz ( k 1 z - k 3 z ) - C 1 ( z , t ) - C* ³ ( z , t ) ].

Уравнение (12) записано при условии к 1 n = = ^к 2 N = ^к 1 ^{- к} 3 .

Установившиеся значения средних заселенностей энергетических уровней при условии, что амплитуды первой волны накачки не зависят от времени, есть

N 10 = ^{N е} ( ^z ) [ I 0 ( ^z ) ^с 21 ⁺⁵ 21 ] ,

N 20 = ^{N е} ( ^z ) I 0 ( ^z ) ^с 12,

где Б ( z ) = [ 1 0 ( z)(G 12 + ^ 21 ) + 5 21 ] ¹

= ^A 20 ⁽ t )

ik dn n ₀ dT

^{5 T} 31 ( ^к 4 , z , t ) ^{+ a} 31 ( ^к 4 , z , t )

x exp [- i^z ( k z ^{- k} 4z ) ^{+ C} 2 ( А t ) ] .

X (10)

Решая уравнение (12) c учетом нача л ьных условий T V j 1 ( к jN , z , t = 0 ) = 0, получим следующее выражение для N ₁₁:

T V 11 = D ( к 1 n , z , t ) exp

t

^{б( z} )

Проинтегрировав по координате z правую и левую части уравнения (10), получим временную зависимость пространственного спектра объектной волны на передней грани нелинейной среды в виде

A 4 ( к 4 , z = 0, t ) = A 20 ( t ) X

где

t

D ( к 1 N , z , t ) = J F ( к 1 N , z , t 1 ) exp

t ₁

^{б( z} )

dt ₁.

t x J dz

ik dn

n ₀ dT

^{5 T} 31 ( ^к 4 , ^z , t ) ^{+ a} 31 ( ^к 4 , ^z , t )

X (11)

Зная заселенности энергетических уровней, можно, используя выражение (2), найти пространственный спектр решетки коэффициента поглощения:

X exp { - iz ( k 2z - k 4 z ) + C 2 ( t , t ) } .

Для нахождения « 0 и a 31 , учитывая изменение интенсивности (5), представим заселенности энергетических уровней в виде

Nj (-, t) = да

= N j 0 + J N j 1 ( к jN , z , t ) exp ( - i к j_N p ) d к j_N , -да

a 31 ( ^к 1 n , ^z , t ) =

t

= ^-CT 12 J I 31 ( ^к 1 N , ^z , t 1 ) ^a 0 ( ^z ) exp

t 1 - t ^{б( z} )

dt ₁,

j = 1, 2.

После подстановки выражения для интенсивности и заселенности энергетических уровней в уравнение (4) оно распадается на два уравнения, одно из которых совпадает по виду с урав-

a₀ ( z ) =----^a 0---- .

^bI 0 ( ^z ) ^{+ 1}

Здесь a0 = NG12 , b = °12 + °21 .

Для нахождения временной зависимости пространственного спектра тепловой решетки 5 T 31 воспользуемся уравнением теплопроводности (3), которое распадается на систему двух уравнений вида

55 T o      d 2 5 T o + « 0 1 0

at        dz2     Cp v , d5 T31     I d2

= х кT 5T31 +

9t      (dz2J a0 A1 "A3 exp {-iz (k1 z - k3z )} + a3110 .

X t ( к, t - t 1 ) =

2ik dn n0Cp vt2 dT

ю z n = 1

П n

( -1 ) n exp

i к t

~2k

V 7

-

^X exp ^L-to2_t ( t ^- t 1 ) 1^X

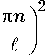
f 2 )²

2 k

V 7

Из выражения (15) следует, что наличие решетки коэффициента поглощения вносит дополнительный вклад в тепловую решетку.

Решение для пространственного спектра тепловой решетки при условии неизменности температуры на гранях нелинейного слоя ( 5 T 31 ( z = = 0 ) = 5 T 31 ( z = t ) = 0 ) представим в виде

г

C     , X • I П n I       I iz к x a (z) sin z exp--

J ^{0 (} ) V t J      I 2 k

0                                      ¹

X R ( t ^- t 1 ) =

ю

t

⁵ T 31 ( ^к 4 ^z ’ t ) = Z J exP ! ⁽7 ( t - t 1 n = 1 L 0

х

- 2 C ( z ) >  dz

31 f

-^ 12 J a 0 ( z ) exp L-2 C ( z ) J exp

^X RT ^(к’ t ^- t 1 ’ t 1

t - t 1 ^{s( z} ).

dz ,

2 ik dn

- t2 ) =--^    °12 X n0Cpvt2 dT

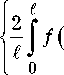
к 4 , z i , t 1 ) sin

П n b z dz dt t 1J 1      1

ю Lf

ZJ

n = 1 L 0

dz a 0 ( z ) 1 0 ( z ) sin I ^ n z

exp

t 1 ^- t 2 ^{s( z} )

. In n I X sin z ,

V t ^J ’

x exp

-2 C ( z ) -

iz к²

2 k

X

где f (Kr zt) = a0 (z) I31 (KT’z’ t) + I0 (z) a31 (KT’z’ t)

n n ( -1 ) n exp

i к t

IT.

-1

X

® n  ^X

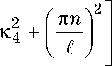
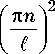
у 7

2 k

V 7

exp ^L-® n ( t ^- t 1 )

Подставив (14) и (16) в (11), получим выражение, описывающее временную зависимость пространственного спектра объектной волны на передней грани нелинейного слоя при четырехволновом взаимодействии с учетом резонансной и тепловой нелинейностей:

Здесь

z

С ( z ) = J a 0 ( z 1 ) dz 1 ,

^к = |^к<| = |^к з|

A 4 ( ^к, ^z = ⁰ , t ) = A 10 ^A 20 ( t ) exp L C 2 ( ^t ’ t ) ] ^X

[ t x |Jxт (к,t -11)A30 (к,t1)dt1 +

t

⁺ J ^х R ⁽ t ^- t 1 ) A 30 ^(к, t 1 ) ^dt 1 ⁺

Выражение (17) с учетом (18)–(20) устанавливает однозначную связь между пространственновременными зависимостями спектров объектной и сигнальной волн.

t t 1

⁺ JJ ^х RT ^(к, t - t 1 , t 1

-

t 2 ) ^A 30 ( ^к, t 2 ) ^dt 2 ^dt 1 f •

—w

При распространении волн накачки строго вдоль оси Z ( к 1 = к 2 = 0 ) в параксиальном приближении весовые функции интегральных операторов х _T , х R и х _RT имеют вид

3. Обсуждение результатов

При наличии только резонансной нелинейности временной отклик четырехволнового преобразователя излучения, определяемый функцией X r , не зависит от поперечной составляющей волнового вектора сигнальной волны. Таким образом, пространственная структура объектной волны во времени не меняется.

При наличии только тепловой нелинейности временной отклик четырехволнового преобразователя излучения, определяемый функцией х т , зависит от величины к, что приводит к изме-

нению во времени качества преобразования излучения.

Учет двух типов нелинейности приводит к появлению в выражении (17) двукратного интегрального оператора, наличие которого существенно усложняет пространственно-временную зависимость спектра объектной волны.

В качестве объектной волны возьмем волну от точечного источника, расположенного на передней грани нелинейного слоя ( A 30 ( к, t ) = 1 ) . Тогда временную зависимость пространственного спектра объектной волны с точностью до постоянного множителя можно представить следующим образом:

Для установившегося (стационарного) режима ( t ^ » ) на нулевой пространственной частоте ( к = 0 ) отношение пространственных спектров объектных волн определяется приближенными выражениями вида

^ = ^A T ~ k [a 0 ^ cth ( a 0 ^ ) -1] dn ^A R      4/ n 0 C p va 0 ^ 12 s    ^dT ’

, = | A Rr | ^     I 0 ^ 12

²    I " A t|    ² I 0 ^C 12 +8 21

^A 4 ( ^K, z = 0, t ) = ^A T ( ^K, t ) + ^A R ( t ) + ^A RT ( ^K, t ) .

Здесь

2 ik  dn

•AT (K, t) = A10A20 exp [C2 (Д t)]-------2 — x n 0 Cpvt dT

V ^X^ l n = 1

п n ( -1 ) n exp

п n ]

¹ J

-

i K t

2k v 7

( к² )²

K k

V 7

-

¹ [1 ^- exp ( -O n t ) ]

® n

{

( п n )

x j а 0 ( z ) sin I — z I exp

-

iz к²

2 k

-

2 C ( z ) dz -,

^A R ⁽ t ) = ^{- A} 10 ^A 20 ^{exp [} C 2 ⁽ А t ) ] ° 12 ^x

Максимальное значение параметра ^ 2 = 0.5 наблюдается при выполнении условия 1 0 ^ 12 >> 8 21 .

Анализ временных характеристик объектной волны при четырехволновом взаимодействии на резонансной нелинейности проводился в работах [10–14], на тепловой нелинейности – в работах [15–18].

При наличии двух видов нелинейности наиболее интересен случай, когда вклад в объектную волну волн, наличие которых обусловлено и тепловой, и резонансной нелинейностями, сравним (^ 1 * 1, ^ 2 * 0.5).

На рис. 1 приведены характерные графики временных зависимостей составляющих пространственных спектров объектной волны. С увеличением времени наблюдается выход составляющих пространственных спектров объектной волны на стационарное значение. Числен-

t                                    Г          Г1

г \    \ гz\-iL x a0 (z) s (z) exp [-2C (z)] 1 1 - exp—

J

0                                       I L V /]

u(23)

> dz ,

ные расчеты проводились для нелинейной среды толщиной t = 10 ³ см с параметрами n 0 = 1.36,

-n = 3.2 ■ 10 ^{- 7} K ^{- 1}, х c p v = 1.66 Дж ■ (см ■ с ■ K) ^{- 1},

2 ik

ART (k, t) = -A10A20 exp LC2 (t, t)]------"2 x n 0 Cpvt

в которой распространялось излучение интенсивностью 1 0 = 10²⁴ фотон ■ см ²с 1 .

Введем времена выхода на стационарное зна-

d.       [ r xjTn122 Jdza0 (z)I0 (z)s(z)sinГГz dr          *                          V t n=1L 0

x

чение составляющих пространственного спектра объектной волны Ат t , Ат r , Ат rt , определяемые из соотношений

x exp

x 1

-2 C ( z ) -

iz к²

2 k

x

|^A i ⁽ t = ^Ат i )| = ¹ A i ⁽ t > ^z ) ,

i = T , R , RT .

1 - to n ,s ( z ) - exp ( -o nn t ) + to n ,s ( z ) exp

^{1 O} n ^{s ( z} ) ] ^O n

t

^{s( z} ) .

Из (23) следует, что время выхода составляющей пространственного спектра объектной волны jA r на стационарное значение можно оценить по формуле

п n

( -1 ) ⁿ exp

i K t

IT,

^Ат R =

ln2

² I 0 ^СТ 12 ^{+ 8} 21

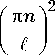
p 7

2 k

V 7

Время выхода составляющей пространственного спектра объектной волны AA т на стационарное значение зависит как от «тепловых» констант ( C p , х ) , толщины нелинейного слоя, так и от

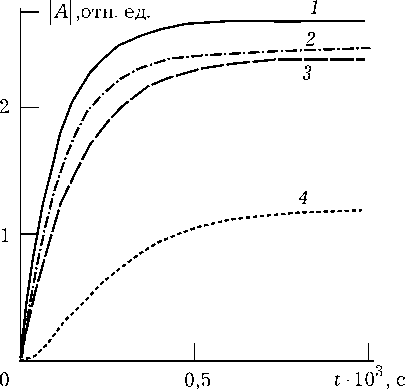
Рис. 1. Временные зависимости составляющих амплитуды объектной волны при к = 0, 0 12 = 3 ■ 10 ^{- 21} см², 8 21 = 10 2 с ^{- 1}, N = 10²²; 1 - А 4 ( t ) , 2 - A т ( t ) , 3 - A r ( t ) , 4 ~ A rt ( t )

пространственной частоты. С ростом значения к время выхода Ат т уменьшается.

Время выхода Ат rt составляющей пространственного спектра объектной волны A rt на стационарное значение при Ат r << Ат т или Ат r >> Ат т определяется max { Ат т , Ат r } . Если Ат т и Ат r сравнимы по величине, то Ат rt можно приближенно оценить по формуле (рис. 2)

Атrt ” РАтт + АтR , где в — коэффициент, зависящий от соотношения Атт / Атr . При изменении Атт / Атr от 0.2 до 5 коэффициент в меняется в пределах от 1.60 до 1.12.

Зависимость от пространственной частоты пространственного спектра волны A rt сходна с аналогичной зависимостью для пространственного спектра волны A т ■

Заключение