Всероссийская олимпиада по элементарной геометрии как одна из форм внеаудиторной учебной работы со студентами

из видов интеллектуальных соревнований студентов, основанных на демонстрации знаний в области одной конкретной учебной дисциплины. Мы согласны с мнением А.И. Попова, что олимпиадное движение обеспечивает «целостность и инновационную направленность педагогического процесса в системе высшего профессионального образования за счет развития творческих способностей обучающихся на основе более глубокого освоения основной образовательной программы и оптимального сочетания педагогического сопровождения формирования кластера профессионально важных творческих компетенций, самоуправления и творческого саморазвития личности студента» и тем самым повышает уровень профессиональной компетентности выпускника вуза [2].

Ввиду этого в целях повышения качества подготовки будущих специалистов, а также поддержки одаренных студентов, способных к креативному и инновационному мышлению, с 2013/2014 учебного года на базе Северо-Восточного федерального университета

АЛЕНА

МИХАЙЛОВНА

ПОПОВА кандидат физико-математических наук, доцент кафедры методики пре

имени М.К. Аммосова проводится Всероссийская олимпиада по элементарной геометрии среди студентов высших учебных заведений. Инициатором проведения и организатором олимпиады является кафедра методики преподавания математики Института математики и информатики Северо-Восточного федерального университета.

Олимпиада проводится в два этапа.

Отборочный этап проводят вузы, заявленные участниками. Организаторы на местах готовят задания и осуществляют отбор участников основного этапа.

Основной этап проводится в очной форме на базе Северо-Восточного федерального университета, а также в дистанционно-очной форме в учебных заведениях, заявленных участниками, в апреле среди

Таблица 1

Количество участников Всероссийской олимпиады по элементарной геометрии, 2014–2019 гг.

Год	2014	2015	2016	2017	2018	2019
Число участников	99	156	318	295	325	521
Количество вузов	6	9	15	18	13	18

победителей и призеров отборочного этапа. Задания высылаются на электронную почту организаторов из других вузов в день проведения Олимпиады. Тексты задач основного этапа составляются не только преподавателями СевероВосточного федерального университета и ведущими учителями математики Республики Саха (Якутия), но и работниками учебных заведений страны. Жюри, состоящее из преподавателей вузов на местах проведения, осуществляет проверку работ участников по разработанным составителями критериям оценивания. После проверки протоколы и отсканированные копии работ участников отправляются организаторам в Северо-Восточный федеральный университет, где проводится перепроверка работ с высокими баллами. По окончании проверки результаты выполнения участниками олимпиадных заданий публикуются на сайте Института математики и информатики Северо-Восточного федерального университета.

Условия, решения заданий и критерии оценивания первых пяти олимпиад по элементарной геометрии приведены в учебном пособии «Решение олимпиадных задач по математике: задачи Всероссийской олимпиады по элементарной геометрии» [3].

С каждым годом география участников расширяется и возрастает число студентов, желающих принять участие в олимпиаде (табл. 1).

В этом учебном году прошла шестая Всероссийская олимпиада по элементарной геометрии. Все участники отметили высокий уровень организации олимпиады и выразили заинтересованность в даль- нейшем сотрудничестве в ее проведении. Организаторы и жюри Олимпиады высоко оценили уровень составления задач, предложили в дальнейшем установить официальные сроки проведения отборочного этапа в вузах и создать банк олимпиадных задач, из которого будут сформированы задания.

Предлагаем условия и решения задач основного этапа IV Всероссийской олимпиады по элементарной геометрии.

Задача 1 . В единичном кубе ABCDA ₁ B ₁ C ₁ D ₁ точки M и N – середины ребер AB и BB ₁ соответственно. Найдите расстояние между прямыми DA ₁ и MN .

Решение . Пусть точка K – середина ребра BC . Тогда плоскости ( A ₁ C ₁ D ) и ( MNK ) параллельны и, следовательно, расстояние между этими плоскостями равно искомому расстоянию. Сечение BB ₁ D ₁ D куба перпендикулярно плоскостям ( A ₁ C ₁ D ) и ( MNK ) и пересекается с этими плоскостями по прямым NE и FD , где E – середина отрезка MK , а F – центр грани A ₁ B ₁ C ₁ D ₁.

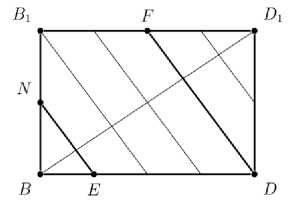
Разделим каждый из отрезков B ₁ D ₁ и BD на четыре равные части и через точки деления проведем прямые, параллельные прямым NE и FD (см. рис.). Теперь видно, что по теореме Фалеса искомое расстояние равно 3/6 · BD ₁ = √3/2 (составитель задачи Н.В. Аргунова).

Задача 2 . Покажите, что треугольник со сторонами 6, 16 и 20 можно разрезать на три различных треугольника с целочисленными сторонами.

Решение . Из теоремы косинусов для треугольника AВC (см. рис.) находим, что cos ∠ BAC = 3/4.

Равенства

6² + 4² – 2 ⋅ 6 ⋅ 4 ⋅ 3/4 = 16, 6² + 9² – 2 ⋅ 6 ⋅ 9 ⋅ 3/4 = 36 и теорема косинусов для треугольников ABE ₁ и ABE ₂ показывают возможность следующего разрезания:

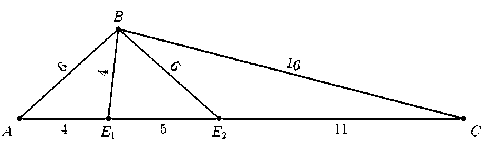
(составитель задачи А.Н. Афанасьев).

Задача 3 . Катеты прямоугольного треугольника расположены на общих внутренних касательных окружностей с радиусами r ₁ и r ₂, а гипотенуза – на общей внешней касательной этих окружностей. Найти площадь этого треугольника.

Решение. SABC = SABCO1 – SACO1, где O1 – центр окружности с радиусом r1. При этом SACO1 = 1/2AC ⋅ r1, л л л ABCO1    ABO1 BCO1

= 1/2 AB ⋅ r ₁ + 1/2 BC ⋅ r ₁ = 1/2( AB + BC ) ⋅ r ₁.

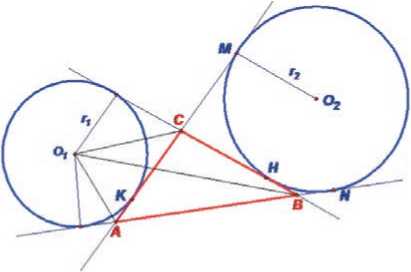
Тогда

S_ACB = 1/2( AB + BC ) ⋅ r ₁ – 1/2 AC ⋅ r ₁ =

= 1/2(( AB + BC + AC ) – 2 AC ) ⋅ r ₁ = 1/2( P_ABC – 2 AC ) ⋅ r ₁ = = ( p – AC ) ⋅ r ₁ = ( AM – AC ) ⋅ r ₁ = CM ⋅ r ₁ = r ₂ ⋅ r ₁

(составитель задачи А.Е. Афанасьев).

Задача 4 . В остроугольном треугольнике ABC точка O – центр его описанной окружности, P – середина отрезка AH , где H – ортоцентр треугольника ABC . Прямая, проходящая через точку P параллельно стороне BC , пересекает стороны AB и AC в точках M и N соответственно. Докажите, что прямые AB и AC задают биссектрисы внешних углов треугольника OMN .

Решение . Пусть BB ₁ и CC ₁ – высоты треугольника. Известно, что треугольники AB ₁ C ₁ и ABC подобны с коэффициентом k = cos ∠ A , AH – диаметр окружности, описанной около треугольника AB ₁ C ₁. Поэтому AP = AH /2 = R cos ∠ A , где R – радиус описанной окружности треугольника ABC . С другой стороны, так как O – центр описанной окружности треугольника ABC , ∠ BOC = 2 ∠ A . Отсюда в прямоугольном треугольнике COT , где T – середина стороны BC , имеем OT = R cos ∠ A . Через точку O проведем прямую, параллельную стороне BC и пересекающую стороны AB и AC в точках K и L соответственно. Так как ранее мы получили AP = OT , по теореме Фалеса следует, что AM = KB и AN = LC . Отсюда и из равнобедренности треугольников AOB и AOC следует, что треугольники KOM и LON также равнобедренные. Тогда ∠ AMN = ∠ MKO = ∠ OMK , откуда и следует, что лучи MA и MB – биссектрисы внешних углов треугольника OMN при вершине M . Аналогично и для вершины N .

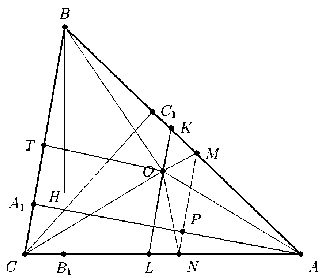
(составитель задачи А.Н. Павлов).

Задача 5. Четыре сферы радиусом a вписаны во все трехгранные углы тетраэдра и касаются внешним образом сферы радиусом b. Найдите радиусы сферы, описанной около тетраэдра, если радиус вписанной в него сферы равен r.

Решение. Рассмотрим тетраэдр T с вершинами в центрах данных сфер. Он подобен исходному те- траэдру, а центры вписанных в них сфер совпадают. Радиус вписанной в T сферы равен r – a, а описанной – a + b. Из подобия имеем: R/(a + b) = = r/(r – a), где R – радиус сферы, описанной вокруг исходного тетраэдра. Значит, R = (a + b)r/(r – a) (состави- тель задачи А.Ю. Эвнин).

Задача 6 . В выпуклом шестиугольнике ABCDEF известно, что AC || DF , BD || AE и CE || BF . Докажите, что S_ABCDEF ≤ S_ACE + S_BDF .

Решение. Пусть ∠CAE = α. Заме- тим, что SABCD = 1/2 ⋅ AC ⋅ BD ⋅ sin α =

= 1/2 ⋅ AE ⋅ BF ⋅ sin α = S_ADEF.

Имеем

^SA BCDEF ^{= S}ABCD ^{+ S}ADEF ^{= 2 √ S}ABCD ^{⋅ S}ADEF ⁼ = 2√1/2 AC ⋅ BD ⋅ sin α ⋅ 1/2 AE ⋅ BF ⋅ sin α =

= √1/2 AC ⋅ AE sin α ⋅ 1/2 BD ⋅ BF sin α =

= 2√ S_ACE ⋅ S_BDF ≤ S_ACE ⋅ S_BDF ,

Таблица 2

Статистика решаемости задач Всероссийской олимпиады по элементарной геометрии 2018/2019 учебного года

	Задача 1	Задача 2	Задача 3	Задача 4	Задача 5	Задача 6
Приступили к решению (%)	91	80	74	68	66	68
Ненулевые решения (%)	38	22	29	6	6	8,4

следовательно, S_ABCDEF ≤ S_ACE + S_BDF (составитель задачи Н.М. Седракян).

В этом году максимальное количество баллов равно 32. В табл. 2 представлена статистика решаемости задач.

Все задания олимпиады рассчитаны на высокий и углубленный уровни геометрической подготовки студентов. Проверка работ показала, что задания олимпиады являются сложными для большинства участников. Самыми трудными оказались геометрические задачи, требующие для решения не столько формальных математических знаний (формул, теорем, готовых алгоритмов), сколько навыков самостоятельного ориентирования в математической ситуации, анализа планиметрической или стереометрической конструкции.

Проведение олимпиады по элементарной геометрии требует серьезной подготовки и объединения усилий организаторов и жюри всех вузов – участников олимпиады. Олимпиада дает студентам возможность проверить приобретенные в стенах вуза знания и умения, сравнить свои возможности и возможности конкурентов, выявить недостатки и сильные стороны, проверить качество освоения профессиональных компетенций. Надеемся, что проведение олимпиады по элементарной геометрии войдет в традицию, а опыт организации подобного мероприятия станет основой для дальнейшего сотрудничества между вузами страны и зарубежья.