Вторая основная связанная задача теории термоупругости для бесконечной полосы

Таким образом, в случае связанной термоупругой задачи необходимо к уравнению (1) прибавить уравнения движения при отсутствии объемных сил, которые можно написать так:

Эхх  dxy = d2u   dyx   dyy = дД dx    dy Р dt2 ’   dx    dy dt2 ’ и связь между компонентами деформации и и и с компонентами напряжения — так:

Ввиду того, что в однородном изотропном теле отсутствуют искажения углов, компонент касательных напряжений остается без изменений:

(du du\

=. = и« =     + аД

Итак, задача состоит в решении системы дифференциальных уравнений (1)-(4) при следующих начальных и граничных условиях:

T($,y,t)|t=o = o, T(x,y,t)\ ,=ЫХД, —    = ДХД у=-Ъ

м(ж,уЛ)||^Нос = 0, у(ж,у,йк=ь = 91(Х,ш), u(x,y,t)\     = у2(Х,ш), y = ±b dT lim ТД, у, t) = 0, lim —— = Q.                        (5)

ж-Юо                ж->|оо dx

Ввиду того, что решается вторая основная задача, в уравнении движения удобнее пользоваться компонентами смещения. Тем самым равенства (3) и (4) примут вид

.86    .       .81    8²«

\Э0    .      „дТ    д2и

(А + ц) — + у Ах - иф— = р——, Эу             Эу dtz а уравнение теплопроводности (1) перепишется так:

д²Т д²Т _ 1 дТ   Э0

Эх2   Эу2 и dt    dt"

Введем термоупругие потенциалы перемещения др д'ф

др

и = — + —, v = — ■ Эх Эу Эу

Внося выражение (7) в системы (6) и (6'), получаем

Эф

Эх ’

(А + 2р)-^-Ар + р-1-Аф -Эх       Эу	ЭТ хр^т-дх	Э2 1 = Pdt2*	^ Эх	д'ф Эу
(Л + 2р^-1-Ар - р-1-Аф -Эу       Эх	ЭТ 9у	Э2 1 = р№'	( др ^Эу	д'ф дх

Эв Л д2Т  д2Т _ 1 дТ

Эх2   Эу2 и dt

Будем считать, что функции и(ж,у,1) и и(ж,у,1) не только непрерывны, но и имеют непрерывные частные производные до третьего порядка включительно в рассматриваемой области.

По указанному выше условию, компоненты смещения и(ж,у,1) и и(ж,у,1) связаны с термоуиругими переменными: „ = $Щ 5» „ = ^ - » функции *,^ и ффх,у,Т) должны иметь частные производные вплоть до четвертого порядка, и будем предполагать, что к этим функциям р^х,у,^ и ф^х,у,^ применима теорема Фурье, т. е. будем считать, что существуют интегралы

У(а,У^) =

W«,y,t) =

ОО

f

х/2тгг J

— ОО

ОО

f

V2tti J

— ОО

ег“х dx,

(/ж,

где а = «1 + гор. Следуя идее Титчмарша [2], в качестве переменной в интеграле Фурье возьмем t и предположим, что функции у(ж,у,^) и '^(ж,у,1) ограничены для всех (ж, у) в заданной области и что существуют интегралы

ОО

ОО

2% J о

2% J о

е^ш1 dt. (10)

Из теорем об обратных преобразованиях Лапласа — Фурье обратное преобразование можно записать в виде

У(«,УЛ)

ОО

/ у(а, у, ш)е^-ш4 dш, о

Ф<№У,Й

ОО

,__ [                dw.

о

(П)

Умножим систему уравнений (8) на -А=еш4 и проинтегрируем по t от 0 до оо. В результате получим

, 9 _А 9 _л ,     э9Т        ₂ /ду 9-ф\

(А + 2/z) —— Ду + р—^-ф — ир—— = —рш I ——Н —— I, ох оу        ох        у ох оу у х 9 л 9 л ,      ,9Т        2 Ф 9<р Эф\

А + 2/z — Ду - р—^'Ф - ир— = -рш² — - — , оу ох        оу        \ оу ох у

92Т  Э2Т    /тX

= ш - ' 7/ДИ '13

ох2   оу2     у ИУ

Умножим систему (12) и (13) на ^^.егаж и проинтегрируем по переменной х с учетом (5) и того факта, что компоненты смещения тфх,у,ф и и(ж, у, f) вместе со своими производными обращаются в нуль при ж —> оо. Будем иметь х                       ,d2 у     d3tb

1а2р-Рш2^-гаирт = ^ dy

—za[—а (Л + 2/z) + рш ]у — za(A + 2/z)    — /z ——— dy2 dy6

г         ~              „ d³p       i               d²ф      dT

— a²(A + 2/z) ---H (A + 2/z)——- - гора² p - рш²) + гар—г - ир— = О, dy           dy⁴                       dy² dy

'²T   / ₂ ш\ 2 d²

• ¹    a -A--= шуа p — шу

и у               dy²

Система (14)-(15) является системой линейных дифференциальных уравнений. Как известно из курса дифференциальных уравнений, систему дифференциальных уравнений можно свести к одному уравнению более высокого порядка. Поэтому естественно искать решения систем (14) и (15) в виде показательных функций вида

у(а, у, ш) = ^\е^ку, 'ф(о1, у, ш) = у2е^к'^и, Т = y₃e^k"^ti,

где ух, 72, 7з и к — неизвестные постоянные, которые нужно определить так, чтобы функции (16) удовлетворяли системе (14), (15). Так как решения ищутся в виде (16), то при подстановке (16) в системе (14), (15) получим

—ш[(А + 2р) (к² — а²) + рш²]71 + ^к² — а²рь + рш²]дг + гариу₃ = О, [(А + 2рРк² - а²) + рш²]71 + га^к² - а²)р + рш²]д₂ - иру₃ = О, шу(^к² — q²)7i + 0 + [ к² — о? — — )73 = 0.

Рассматривая (17) как систему линейных однородных алгебраических уравнений относительно 71, 72, 73, замечаем, что для получения нетривиальных решений систем (14) и (15) надо потребовать равенства нулю определителя, составленного из коэффициентов линейных однородных алгебраических уравнений (17). Одновременно этот определитель является характеристическим уравнением систем (14), (15):

—ш[(А + 2рРк² — а²) + рш²\ рк² — а²)р + рш²^к [(А + 2р^к² — а²) + рш²^к га[(&² — а²)р + рш²]

шрре² — а²')                     О

гаир

— ирк к2 - а2 + ^

= 0.

Раскроем определитель по минорам:

к^к² — а²рь + рш²]

или

[(А + 2рРк² — а²) + рш²^к шр^к² — а²)

■ 2<т[(&² — о?рь \ рш^]

— ирк

(к² - а²) + ^

—ш[(А + 2рРк² — а²) + рш²] шр^к² — а²)

гаир к2 - а2 + ^

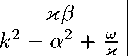
Из (19) получаем следующее:

(А + 2рРк² — а²) + рш² шр^к² — а²)

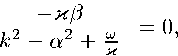
(к² — а²) рк² — а²рг + рш²]

откуда имеем к2 — а2 = 0,  (к2 — а2рг + рш = 0,

[(А + 2р,рк² — а²) + рш²рк² — а² + ш/и) — рш(&² — а²^ир = 0.

Итак, &i_;2 = ±а, кз-д = ±у/а² — рш²/р

^² - а² = -    * [рш² + ршир + (А + 2ц)-]

2(А + 2р)                      и рш2 + ршир + (А + 2р) —

+2шрир

рш² + (А + 2ц)- и

Корни характеристического уравнения различны, поэтому система дифференциальных уравнений имеет линейно зависимые решения, т. е. 71, 72, 73 будут линейно зависимыми. Подставляя значение а = к^, будем иметь гарш2у\ + рш2«72 + гаируз = 0, рш2«71 + гаршу2 — хра^з = 0, шр • 0 + 0 + ^7з = 0,

7з = 0,

71 = сь

72 = -'ici-

Аналогично, подставляя к₂ = —а, имеем 73 = 0, 72 = ic^, 71 = С2.

Подставим корень кз4 = а² — ^-;

{ ia^^p^yi + гахру₃ = О, -^рш²71 - хРу₃ = О, -шррш²У1 - (рш² + ^)7з = О,

7з = с₃₎ 71 = сз—~~—г, 72 = 0, рш²^Х + р)

7з = С₄, 71 = С4 —— 7, 72 = 0. рш-рХ + /И

Введем обозначение:

™^{2 =} ом I о a W ^{+ Т}1^ШХР + (^Л + ²М)-]

2(А + 2р)х

± хНршхРУ + W - (А + 2р)-)² + 2wyxp(pw² + (А + 2р)—

V                     XX

—га[(А + 2р)т² + рш²]7₄ + (т²р + рш²) V а² + т²7₂ + гахРуз = 0,

[(А + 2р)т2 + рш2]71 V«2 + т2 + гарн2 р + рш2)7г — хр\/ а2 + т2 = 0,**

• 2        /   2    ^ iп

шт^т 71 + т--7з — 0.

\ х/

Согласно определению комплексного числа, два комплексных числа равны между собой тогда и только тогда, когда соответственно равны их действительные и мнимые части. Учитывая это, получаем, что д2 = 0, и это приводит систему (24) к виду

• -[(А + 2р)т² + рш²]71 + хруз = 0,  [(А + 2р)т² + рш²\ух - хру₃ = 0.

Отсюда определим неизвестные 71, 72, 73:

(А + 2р^т² + рш²

71 = Сб, 72 = 0, 7з = -----------------• хр

Аналогично, подставляя значение к6 = —Va2 + m2, получаем п         (А + 2ррп2 + рш2

71 = Сб, 72 = 0, 7з = с₆-------------------.

хр

Теперь можно записать общие выражения искомых функций

• (      \ a-и -ау Хрре^кзу       Хрре^-кзу      _к        __к

<р(а,у,ш) = ще ^у + с₂е ^u - с₃ —т-——г + с₄—т-——- + с₅е^^5У + с₆е ^ksU, pw²VX + p) pw²vX + p)

Р = -iC1eay + гс2е"ау, т                  ^Х + 2ррп2 + рш2 1 „ —кчУ\

Т = сзе^кзиС4в                 ---L ---(_С5е^5У__Сбе к₅уу

Хр

Вернемся к компонентам смещения и (ж, у, t) и у (ж, у, t) и, учитывая термоупругий потенциал перемещения, можем их записать так:

dp                dtp и\а,у,ш) = — гар 4——, у(а,у,ш) = —--Угаф, dy              dy

м(а,у,ш) ,, = О, у(а,у,ш) = а₄(а,шР v(a,y,u)\    , = а₂(а,шУ

X ’ ' М-у = ±Ь     ¹            П-у = Ъ ^{У Х п х 1}     Ч-у = — Ь             ’

Преобразовывая начальные и граничные условия, можем представить их в виде

—2?a[cie“^y + сге ^ау] 4--^“ , ^ , [сзе^³^⁷ — с₄е ^fcsy] 4- ?a[c5e^fcsy — Сбв ^fcsy] = м(а, у, ш),

2a[cie“^y — С2е^-“^у]^ [cse^fc3y + С4е^-/,'^зУ] + k₅\c5e^ksy — сев^-fc5y] = у(а,у,ш), pw^z^X + p)

Т(а,у,ш) = cse^fc3y 4- С4е^-,,'^зУ 4- c?[cse^fc5y — cee^-fc5y], (А + 2р)т² 4- рш²

Подставляя значения граничных условий в преобразованном виде, получаем систему алгебраических уравнений для определения произвольных постоянных щ, с₂, сз, С4, С5) Cg .

2cie“^b + 2с₂е-“^ь + тсзе^⁶ - тс₄е"^кзЬ - с_ъе^к^^ь - с₆е-^к^^ь = О,

2cie"“^b 4- 2с₂е“^ь 4- тс₃е"^кзЪ - тс₄е^кзЬ - c₅e"^ksb - c₆e^ksb = О, 2ae^abci — 2ас2е^-“^ь — тк₃с₃е^кзЬ — тк₃С4е^-кзЬ 4- к₃с₃е^кзЬ 4- к₃Сбе^-кзЪ = gi(a,cy), 2acie^-“^b — 2ае“^ь — тк₃с₃е^-кзЪ — тк₃С4в^кзЬ 4- k₃c₃e^-ksb 4- к₃Сбе^кьЪ = д₂^а,шУ с₃е^кзЪ + с₄е-^кзЬ + dc₅e^k5b - c₆e-^k5b = .fMw^ к₃с₃е^-кзЬ — к₃с₄е^кзЬ 4- dc5k5e^-ksb 4- dk5C6e^ksb = /₂(а,ш),

, (Л 4- "21фт2 4- рш2             ирр d = --------«------’ 7711 = ——?■ хр                 pwz^X 4- р-)

Решая эту систему алгебраических уравнений относительно Cj (j = 1, 2, 3,4, 5, 6), получим, что Aq равно определителю

Ai	△ 2	A3	A.	△ 5	Ae
C1 Ao’	C2 “ A?	C3 “ A?’	C4" Ao’	C5" A?	С6" a;

Подставляя найденные значения произвольных постоянных (ci,C2, сз,С4,С5,Сб) в искомые функции, получим

у(а,у,ш) = ^еау	+ ^1е-«У _ ^1екзУ До      До	До	+ ^ек^ + До	^1р-к6у До
	ф =       + До	А2 г-А""у, До
Т(а, у, ш)	= ^1екзУ + ^±е-кзУ До     До	+ d^ До	-d^e"^ До

Так как функции у(а,у,ш) и ффа, у, ш) найдены, то компоненты смещения будут определяться по формуле (7), а компоненты напряжения — по формуле (3).