Вторичные режимы конвекции жидкости с вязкостью, зависящей от температуры, в плоском вертикальном слое

При наличии горизонтального градиента температуры механическое равновесие жидкости невозможно, возникает конвективное движение, интенсивность которого растет с увеличением разности температур. По сравнению с неустойчивостью равновесия явление неустойчивости конвективного течения обладает рядом особенностей. Этот вид неустойчивости — результат развития возмущений на фоне движущейся жидкости, поэтому важнейшим фактором является взаимодействие возмущений с основным потоком. Исследования показали, что существует три механизма неустойчивости конвективных течений. Первый — связан с передачей энергии от основного течения к возмущениям скорости при больших скоростях. Второй — обусловлен стратификацией, которая может быть следствием условий нагрева или возникает вследствие течения определенной структуры. Третий механизм заключается в генерации нарастающих волн, и для него существенно взаимодействие нестационарных тепловых и гидродинамических возмущений.

Типичным конвективным течением, на примере которого отчетливо проявляются основные особенности неустойчивости, служит течение в слое между вертикальными параллельными плоскостями, нагретыми до разных температур. Устойчивость конвективного течения в слое жидкости с постоянной вязкостью впервые рассмотрена Г.З. Гершуни [1, 2]. Он показал, что характеристики конвекции в этом случае зависят от числа Прандтля и числа Грасгофа.

Обычно при исследовании свободной тепловой используется приближение Буссинеска, в котором переменность плотности учитывается только в слагаемом, описывающем подъемную силу в уравнении движения. При этом в большинстве случаев считается, что коэффициенты вязкости и теплопроводности постоянны. Однако во многих ситуациях при определении условий возникновения неустойчивости в потоках важно принимать во внимание непостоянство теплофизических параметров. Наиболее существенна температурная зависимость вязкости. Ее учет особенно значим при изучении устойчивости течений высоковязких жидкостей, поскольку в таких жидкостях интенсивная конвекция и неустойчивость возникают при больших разностях температур.

В плоском вертикальном слое жидкости с вязкостью, зависящей от температуры, и разными температурами на границах возможно плоскопараллельное течение, в котором сохраняется обычное линейное распределение температуры, но возникает деформация поля скорости [3], обусловленная температурной неоднородностью вязкости. Первая попытка решения задачи устойчивости конвективного течения жидкости с вязкостью, зависящей от температуры, в вертикальном слое при нагреве сбоку предпринята в работе [4], где применен метод Галеркина с простейшими аппроксимациями амплитуд. Сделан вывод о понижении порога устойчивости. Решение задачи методом пошаговой ортогонализации, обеспечивающим достаточную точность получения характеристик устойчивости, осуществлено в [5] (также см. [6]).

В работе [7] анализировалась линейная устойчивость механического равновесия в плоском горизонтальном слое жидкости с вязкостью, нелинейно зависящей от температуры. Результаты хорошо согласуются с экспериментом, проведенным авторами для водно-глицериновой смеси. В [8] выполнен линейный анализ устойчивости конвективного течения жидкости с вязкостью, являющейся экспоненциальной функцией температуры, в плоском наклонном слое.

Цель настоящей работы состоит в исследовании вторичных режимов конвекции в жидкости с переменной вязкостью между двумя вертикальными параллельными плоскостями, нагретыми до разных температур.

2.    Постановка задачи и основные уравнения

Рассмотрим вертикальный слой вязкой несжимаемой жидкости, заключенный между двумя параллельными твердыми плоскостями, на которых поддерживаются разные постоянные температуры. Введем декартову прямоугольную систему координат следующим образом: ось z направим вертикально ввер х, ось x — перпендикулярно границам слоя, начало координат поместим посередине слоя. Будем полагать, что неоднородности температуры малы; в этом случае можно считать, что плотность и динамическая вязкость жидкости линейно меняются с ростом температуры: р = р ₀ [ 1 -р ( T - T_o ) ] , п = п ₀ [ 1 - s ( T - T_o ) ] , где T ₀ — температура, принимаемая за начало отсчета.

Для описания поведения жидкости будем использовать систему уравнений свободной тепловой конвекции в приближении Буссинеска:

d v               1 „     „      1

— + ( v V ) v =-- V p + g P T y + --div т ,

5 t               P o                 P o

6T ,

— + (vV)T = xA T, о t div v = 0, где v — скорость жидкости, p — давление, T — температура, отсчитываемая от T0 , τ — тензор вязких напряжений

т = П( T)

Z d vi + dvk _ dxk dxi

P o

плотность при температуре T _o, x — коэффициент

температуропроводности, p — коэффициент теплового расширения, g — ускорение свободного падения,

γ — единичный вектор, направленный вертикально вверх.

Выберем следующие единицы измерения: для длины — полутолщину слоя d , для скорости — П ₀/( р ₀ d ), для времени — р ₀ d ² /п ₀, для давления — П 2/( Р ₀ d ), для температуры — полуразность температур на вертикальных границах 0 . Уравнения в безразмерной форме принимают вид:

d v

— + ( v V ) v = -V p + div т + Gr Т Y ,

— + ( v V ) T = Pr ^{- 1} A T , д t ^{v 1}                 ’

div v=0,     vt = (1 - aT) —i- + —k- ik

( д X k   д х ^

,

и содержат следующие безразмерные параметры: число Грасгофа Gr = g р© d ³/(П о/Ро ) 2 , число Прандтля Pr = П _о/( р _о х ) и параметр a = e/© , определяющий зависимость вязкости от температуры. Для безразмерных переменных сохранены прежние обозначения.

Ограничимся рассмотрением плоской задачи: v y = 0, д/д у = 0 . В этом случае удобно ввести функцию тока у , связанную с компонентами скорости соотношениями:

ду дz ’

Vz =     , дх

и завихренность течения ф = rot y v = -Av .

Применяя к уравнению движения операцию rot _y и используя выражения (4), получим уравнения в терминах функции тока и завихренности:

дф + ду дф-ду дф = , Г д 2ф + д2ф^ + 2 Г дf дф_+д/_ дф)- 4 д2 f д 2у  ( д2 f  д2 f Уд 2у  д2у) + Gr дТ_дt дх дz дz дх   J ( дх2 дz2J (дх дх   дz дz J дхдz дхдz  (дх2   дz2 JI дх2   дz2J дх ’

д Т ду д Т дуд Т Г 1Т д2 т д2 Т

+                  = Pr 11     +   2

д t дх дz дz дх       ( дх2 дz2

ф =

Г д у д у I ( дх2 дz2 J,

f = 1 -a Т .

На твердых границах слоя выполняются условия прилипания и заданы разные постоянные температуры:

х = _Т 1: ^д»= о, ^= 0, Т = ± 1. д z        д х

3.    Метод решения

Задача (5), (6) решалась численно методом конечных разностей. При дискретизации уравнений все пространственные производные аппроксимировались центральными разностями. Использовалась явная конечно-разностная схема. Решение уравнения Пуассона для функции тока находилось методом последовательной верхней релаксации. Значения завихренности на вертикальных границах вычислялись по формуле Тома: ф ₀ , _k = - (2/ Л _х ²) у 1, _k [9]. Размер расчетной области по вертикали — H , соответствовал длине волны наиболее опасных возмущений. На горизонтальных границах области для всех функций ставились условия периодичности.

В расчетах использовалась равномерная сетка с прямоугольными ячейками. Шаг сетки по горизонтали составлял 2 30 , по вертикали — H 150 . Шаг по времени выбирался из условия устойчивости и принимался равным A t = h/l ( 32 ( 1 + |у_mаx |)) [10].

Для определения порога неустойчивости плоскопараллельного течения решалась полная система нестационарных нелинейных уравнений; на каждом временном шаге по полю температуры находилось число Нуссельта, которое должно быть равным единице для плоскопараллельного течения и превышать единицу для вторичных режимов течения. Критическое число Грасгофа находилось по зависимости Nu ( Gr ) .

4.    Основное течение. Линейная устойчивость основного течения

Известно, что в слое жидкости, заключенном между двумя параллельными плоскостями, нагретыми до разных температур, возникает подъемно-опускное течение, которое является устойчивым до тех пор, пока число Грасгофа не достигнет некоторого критического значения. При Pr = 1 для жидкости с постоянной вязкостью (а = 0) критическое значение числа Грасгофа составляет примерно 496.

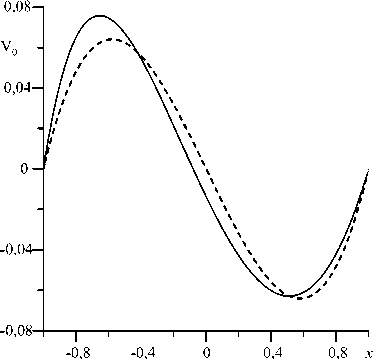
Рис. 1. Профили нормированной скорости основного течения для жидкостей с постоянной (штриховая линия) и переменной (сплошная линия) вязкостями

На рисунке 1 представлены профили скорости основного течения жидкости с постоянной вязкостью ( а = 0) и жидкости с вязкостью, линейно зависящей от температуры, при а = 0,5 (вязкости у холодной и горячей границ слоя при этом а отличаются в 3 раза). Как видно, переменность вязкости приводит к несимметричности профиля скорости относительно линии x = 0: координата, при которой скорость обращается в нуль, смещена к горячей стенке, максимальное значение скорости в левой (более нагретой) половине слоя больше, чем в холодной. Эти результаты качественно соответствуют результатам из [6].

Расчеты, проведенные в [6], показали, что для жидкости с вязкостью, зависящей от температуры, как и для жидкости с постоянной вязкостью, при малых значениях числа Прандтля наиболее опасной является монотонная гидродинамическая мода неустойчивости, проявляющаяся как вихри на границе встречных потоков. При числах Прандтля, больших некоторого значения, опасной становится колебательная мода неустойчивости, представляющая собой тепловые волны.

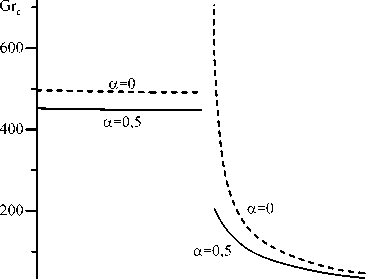
На рисунке 2 а приведены рассчитанные автором границы устойчивости стационарного плоскопараллельного течения для обеих мод неустойчивости на плоскости параметров «число Прандтля–число Грасгофа» для жидкости с постоянной вязкостью и для жидкости с вязкостью, зависящей от температуры по линейному закону с коэффициентом пропорциональности 0,5. По рисунку видно, что переменность вязкости приводит к дестабилизации стационарного плоскопараллельного течения по отношению к обеим модам неустойчивости: критические значения числа Грасгофа уменьшаются по сравнению со случаем постоянной вязкости. Числа Прандтля Pr*, при котором происходит смена типа неустойчивости, ведет себя аналогичным образом.

Рисунок 2б содержит нейтральные кривые Gr(к) для Pr = 20 и а = 0,5 . Как видно, при этом значении числа Прандтля имеются две моды неустойчивости, причем наиболее опасными являются колебательные возмущения (им соответствует нижняя нейтральная кривая). Отметим, что в приведенном на рисунке диапазоне волновых чисел область чисел Грасгофа, в которой колебательные возмущения нарастают, ограничена не только снизу, но и сверху.

о

ю

Рг 100

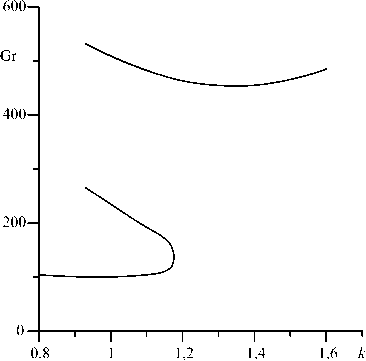
Рис. 2. Зависимости минимального критического числа Грасгофа от числа Прандтля для монотонной и колебательной мод неустойчивости у жидкостей с постоянной и переменной вязкостями ( а ); нейтральные кривые Gr( к ) при Pr = 20 и а = 0,5 ( б )

5. Вторичные режимы течения, возникающие в результате неустойчивости стационарного плоскопараллельного течения при малых числах Прандтля

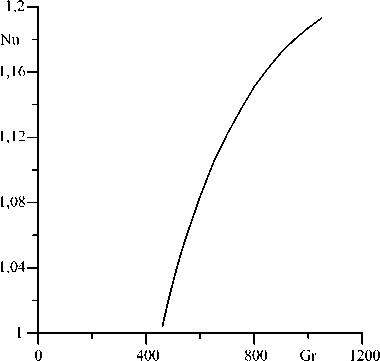
Рис. 3. Зависимость числа Нуссельта от числа Грасгофа для вторичных стационарных режимов конвекции при Pr = 1, а = 0,5, к = 1,4

Численные расчеты вторичных режимов проводились для двух значений числа Прандтля: Pr = 1 и Pr = 20 . При Pr = 1 потеря устойчивости основного течения связана с развитием гидродинамических возмущений, представляющих собой вихри на границе встречных потоков, при Pr = 20 за неустойчивость основного течения ответственны колебательные возмущения, являющиеся тепловыми волнами.

Обсудим случай Pr = 1, для которого на рисунке 3 приведена зависимость числа Нуссельта от числа Грасгофа при а = 0,5 и к = 1,4. Видно, что вблизи порога возникновения вторичного течения число Нуссельта растет с изменением числа Грасгофа по корневому закону, то есть вторичные режимы конвекции возбуждаются мягко. На рисунке 4 показаны линии тока и изотермы вторичных стационарных режимов конвекции при двух значениях числа Грасгофа.

Число Gr = 460 очень близко к пороговому значению 452, определяющему неустойчивость

плоскопараллельного течения, поэтому

течение почти

не отличается от плоскопараллельного, а изотермы слабо искривлены. При числе Gr = 550 наблюдается значительное отличие линий тока и изотерм от тех, которые соответствуют плоскопараллельному течению: хорошо видны вихри на границе встречных потоков, изотермы сильно искривлены. Отметим также несимметричность полей функции тока и температуры относительно вертикальной оси, проходящей

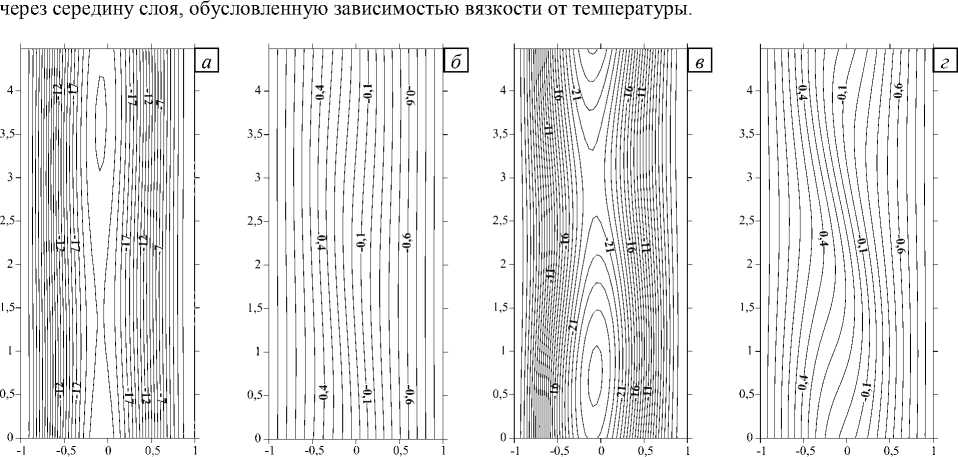
Рис. 4. Линии тока (а, в) и изотермы (б, г) вторичного стационарного режима конвекции при

Pr = 1, а = 0,5, к = 1,4 и различных значениях числа Грасгофа Gr : 460 (а, б); 550 (в, г)

Анализ результатов показал, что при наличии зависимости вязкости от температуры вторичные режимы конвекции, возникающие при Pr = 1 в результате неустойчивости стационарного плоскопараллельного течения по отношению к гидродинамическим возмущениям, представляют собой не неподвижные, как в случае жидкости с постоянной вязкостью, а дрейфующие в вертикальном направлении вихри на границе встречных потоков. Для иллюстрации этого на рисунках 5, 6 показана временная эволюция течения при Pr = 1, а = 0,5, Gr = 550 (Рис. 5), а также, для сравнения, в отсутствие температурной зависимости вязкости ( а = 0) при тех же значениях прочих параметров (Рис. 6).

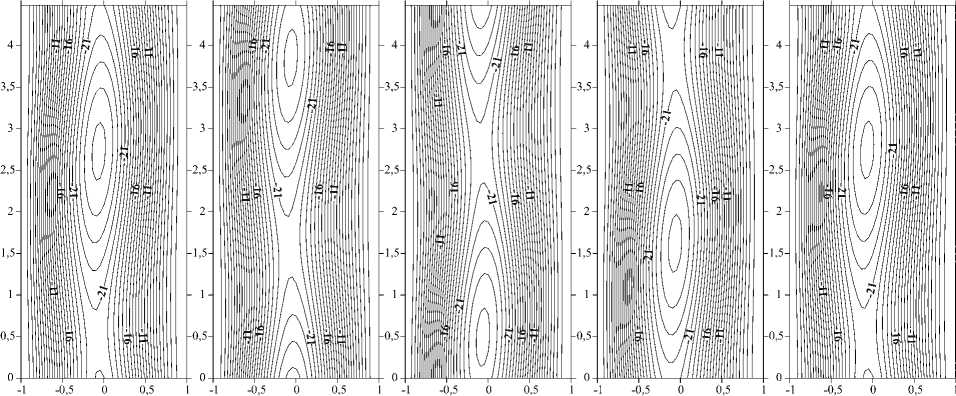
Рис. 5. Временная эволюция течения при а = 0,5, периода колебаний

Pr = 1, к = 1,4 , Gr = 550; изменение линий тока приведено через 1/4

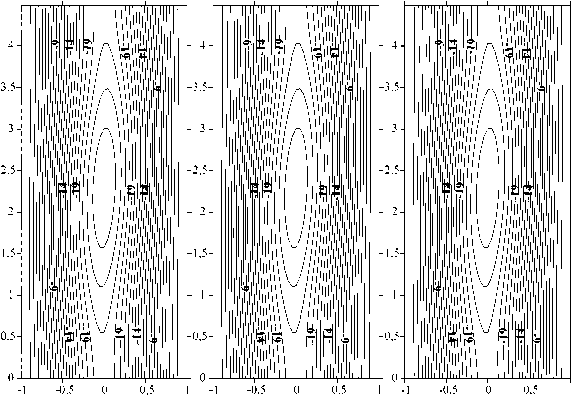
Рис. 6. Временная эволюция конвективного течения при а = 0 , Pr = 1, к = 1,4 , Gr = 550 ; изменение линий тока через 1/2 периода колебаний

На рисунке 7 приведено число Нуссельта как функция времени для жидкости с вязкостью, зависящей от температуры ( а = 0,5) при Pr = 1, к = 1,4, Gr = 550 . Видно, что после переходного процесса наблюдаются стационарные колебания Nu около некоторого среднего значения (форма колебаний числа

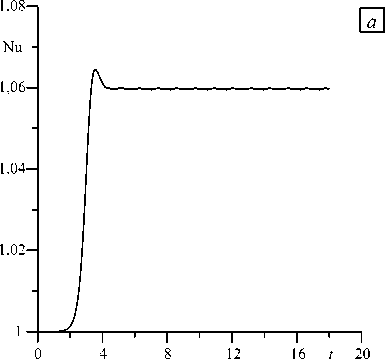
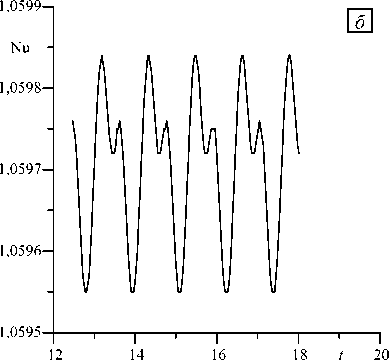
Рис. 7. Зависимость числа Нуссельта от времени при Pr = 1, к = 1.4, Gr = 550 для жидкости с переменной вязкостью ( а ); участок кривой в увеличенном масштабе ( б )

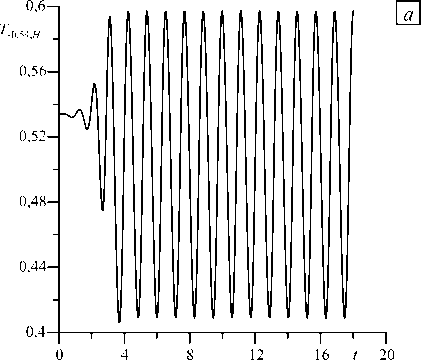
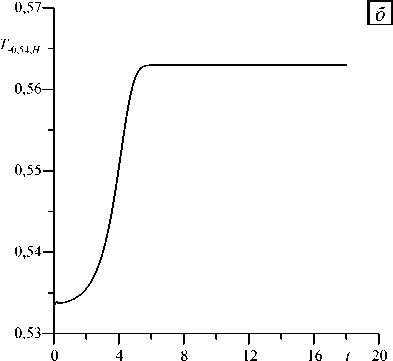
Рис. 8. Изменение температуры в точке с координатами (-0,54, H ) во времени при Pr = 1 , к = 1,4 , Gr = 550 для жидкости с вязкостью, зависящей ( а = 0,5) ( а ) и не зависящей ( а = 0 ) ( б ) от температуры

Нуссельта для жидкости с переменной вязкостью показана в увеличенном масштабе на рисунке 7 б ). В случае жидкости с постоянной вязкостью число Нуссельта после переходного процесса выходит на постоянное значение.

Рисунок 8 иллюстрирует эволюцию во времени локальных характеристик поля температуры при тех же значениях параметров для жидкостей с переменной и постоянной вязкостями. Как видно, в жидкости с переменной вязкостью после переходного процесса устанавливаются стационарные колебания локальных характеристик поля температуры (Рис. 8 а ), а в жидкости с постоянной вязкостью эти характеристики выходят на постоянное значение (Рис. 8 б ).

Таким образом, вторичный режим, возникающий после потери устойчивости стационарного плоскопараллельного течения жидкости с вязкостью, зависящей от температуры, характеризуется наличием волны, распространяющейся вдоль слоя. Фазовая скорость волны монотонно растет с увеличением числа Грасгофа, при Gr = 550 она равна примерно 3,8, а при Gr = 1050 — примерно 4,1.

6.    Вторичные режимы течения, возникающие в результате неустойчивостистационарного плоскопараллельного течения при больших числах Прандтля

Перейдем к случаю Pr = 20. При этом за неустойчивость основного течения ответственны колебательные возмущения, представляющие собой тепловые волны. На рисунке 9 показана зависимость числа Нуссельта от числа Грасгофа для вторичных режимов конвекции при Pr = 20 , к = 0,93. Как видно, при увеличении числа Грасгофа вплоть до примерно 102 число Нуссельта остается равным единице, что соответствует режиму стационарного плоскопараллельного течения. Значение Gr = 102 соответствует точке нижней ветви нейтральной кривой колебательной неустойчивости при к = 0,93, приведенной на рисунке 2 б .

В диапазоне от 102 до 180 число Нуссельта растет с увеличением числа Грасгофа по закону, близкому к корневому, то есть наблюдается мягкое возбуждение вторичного конвективного движения.

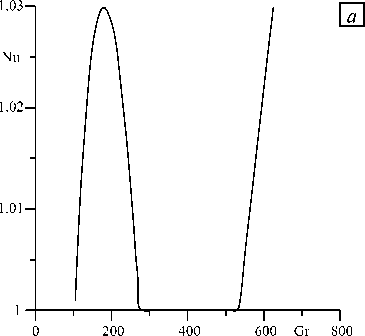
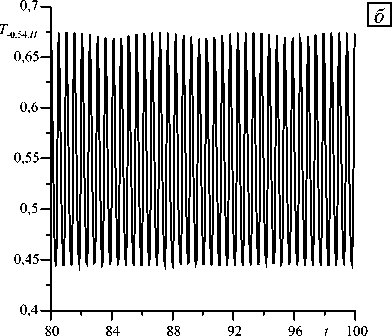
Рис. 9. Зависимость числа Нуссельта от числа Грасгофа ( а ) и временная эволюция температуры в точке с координатами (–0,54, H ) при Gr = 190 ( б ); Pr = 20, а = 0,5, к = 0,93

При дальнейшем росте числа Грасгофа число Нуссельта уменьшается до значения, равного единице, достигаемого при Gr ® 275. Это поведение объясняется приближением к точке на верхней ветви нейтральной кривой колебательной неустойчивости при к = 0,93 (см. Рис. 2 б) . В интервале значений числа Грасгофа от 275 до 532 число Нуссельта остается равным единице, что соответствует режиму стационарного плоскопараллельного течения. При числах Грасгофа, бо _́ льших примерно 532, число Нуссельта вновь растет. Это связано с тем, что осуществляется переход в область монотонной неустойчивости (см. Рис. 2 б ).

На рисунке 9 б приведена температура как функция времени в точке с координатами (–0,54, H ). Как видно, имеют место модулированные колебания.

Линии тока и изотермы вторичного течения при Pr = 20, а = 0,5, к = 0,93, Gr = 190 показаны рисунке 10. Для сравнения на том же рисунке приведены линии тока и изотермы вторичного течения при Pr = 20 , а = 0, к = 0,8, Gr = 200 . Как видно, имеет место значительная асимметрия поля температуры вторичного режима конвекции в случае жидкости с вязкостью, зависящей от температуры, что, по-видимому, связано с тем, что вследствие переменности вязкости равноправие тепловых волн, бегущих вверх и вниз, нарушается [6], и, при выбранных значениях параметров волна, бегущая вверх, нарастает, а волна, бегущая вниз, затухает.

Рис. 10. Линиитока ( а , в ) и изотермы ( б , г ) вторичных режимов конвекции при Pr = 20 ; а = 0,5, к = 0,93 , Gr = 190 ( а, б );

а = 0, к = 0,8, Gr = 200 ( в, г )

7.    Заключение

Исследована устойчивость стационарного плоскопараллельного течения вязкой несжимаемой жидкости с вязкостью, зависящей от температуры, между двумя вертикальными параллельными плоскостями, нагретыми до разных температур. Расчеты показали, что при Pr = 1 наиболее опасной является монотонная гидродинамическая мода неустойчивости, а при Pr = 20 — колебательная мода неустойчивости.

Проанализирован характер возбуждения неустойчивости и вторичные режимы конвекции. Найдено, что вторичные режимы конвекции возбуждаются мягко.

Получены зависимости характеристик течения и теплопереноса от числа Грасгофа при различных числах Прандтля. Показано, что при малых числах Прандтля вторичные режимы течения представляют собой дрейфующие вихри на границе встречных потоков. При больших числах Прандтля имеются две моды неустойчивости: монотонная и колебательная. Наиболее опасны колебательные возмущения, причем область колебательной неустойчивости ограничена сверху и снизу. Это приводит к тому, что связь числа Нуссельта с числом Грасгофа становится немонотонной.