Вторичные течения Прандтля 2-го рода в пространственно-неравновесном турбулентном течении

Одно из интересных и важных с практической точки зрения проявлений турбулентности — способность вызывать так называемые вторичные течения. Эти организованные движения жидкости в плоскости, перпендикулярной направлению основного потока, называются вторичными течениями Прандтля 2-го рода. Неоднородность поля течения в направлении размаха изменяет локальные свойства турбулентности потока, что порождает градиенты напряжений Рейнольдса, которые и приводят к возникновению вторичных течений. В настоящее время накоплен обширный научный материал о свойствах турбулентных течений при наличии вторичных течений [1]. Среди прочих, интересен обнаруженный недавно эффект опережающего роста конвективного теплообмена по сравнению с ростом трения на твёрдых стенках плоского канала при наличии продольных рёбер, которые создают вторичные течения [2]. Этот эффект имеет потенциал прикладного использования при создании новых эффективных теплообменных поверхностей.

Решение этой проблемы особенно актуально для турбулентных режимов течения теплоносителя, наиболее часто реализующихся в инженерных приложениях. В этой связи интересна возможность сочетания эффекта интенсификации теплообмена вторичными течениями с известными эффектами изменения теплообмена в динамически неравновесных турбулентных потоках: течениях в трубах с пульсирующим расходом, течениях с продольным градиентом давления (например, в сужающихся и расширяющихся каналах) [3].

Задачей настоящей работы является изучение особенностей развития вторичных течений и изменений теплогидравлических свойств оребрённой поверхности в изменяющемся в пространстве динамически неравновесном турбулентном потоке. В работе не ставится задача отыскания оптимальных компоновок, дающих максимальный эффект. Целью является выявление качественных закономерностей в условиях максимального упрощения модельной постановки, обеспечивающей, тем не менее, требуемые условия.

2.    Постановка и метод решения задачи

Рассматривается течение вязкой несжимаемой жидкости в плоском длинном и широком канале высотой h : x = ( x , у , z ) e {| x| <^ , 0 <  у <  h , | z | < от } . Нестационарные поля скорости u ( t , x ) = ( u , v , w ) , температуры 6 ( t , x ) и кинематического давления p ( t , x ) отыскиваются путём численного решения уравнений Навье–Стокса и энергии в следующем виде:

^u + (uV)u = -Vp + uAu , Vu = 0 , d^ + («V)0 = aA0 + Q0.

Здесь и — кинематическая вязкость, а — коэффициент температуропроводности. Температура рассматривается как пассивная примесь, влиянием термических эффектов на поле скорости пренебрегается.

В продольном направлении x и боковом направлении z используются условия периодичности. Величины продольного L_x и бокового L_z периодов выбираются достаточно большими, для надёжного воспроизведения известных из литературы характеристик турбулентного течения в плоском канале. Средний градиент давления, обеспечивающий движение жидкости, определяется в каждый момент времени из условия сохранения постоянного расхода. В базовой постановке задачи на одной из стенок канала у = 0 ставятся условия прилипания. Противоположная стенка у = h считается непроницаемой и свободной от касательных напряжений. Такая постановка отличается от традиционной постановки при расчёте турбулентных течений в плоском канале, когда на обеих стенках задаются условия прилипания. Течение в рассматриваемой постановке можно интерпретировать как течение в канале удвоенной высоты: 0 <  у <  2 h , в плоскости симметрии у = h которого вводится искусственное условие симметрии течения. Это условие несколько ограничивает движение турбулентных структур и искажает течение при y ~ h , но, как показано в нескольких исследования (см., например, [4]), для течения в пристенной и средней области канала приводит к результатам, близким к традиционной постановке. Необходимый объём вычислений сокращается при этом вдвое. Поскольку в данной работе наибольшее внимание уделяется области течения, примыкающей к твёрдой стенке у = 0 , то такое упрощение можно считать оправданным. Для образности изложения твёрдую стенку будем именовать нижней, а свободную — верхней. Эта терминология в данном случае не предполагает наличие силы тяжести и связанных с ней сил плавучести. Температура нижней стенки считается постоянной (для определённости она полагается равной нулю), а верхняя стенка — теплоизолированной ( д0/д у = 0). В правую часть уравнения для температуры добавлен источник тепла Q ₀ ( t ) , который обеспечивает сохранение постоянного уровня средней по объёму температуры T b , заданной начальными условиями. В начальный момент времени распределения температуры и продольной компоненты скорости принимаются параболическими по форме: u/u b = 0/ T b = 1.5 ( у/h )( 2 - у/h ) , с добавлением некоторого трёхмерного бездивергентного возмущения скорости. Расчёт ведётся до установления статистически стационарного режима. После этого расчёт продолжается с параллельным вычислением интересующих средних характеристик, которые не зависят от конкретного вида начального возмущения при условии его трёхмерности и достаточной интенсивности. Расчётная сетка в базовой постановке равномерная в однородных направлениях x и z и неравномерная, со сгущением вблизи твёрдой стенки, в направлении y .

При моделировании течений в оребрённом канале на его нижней стенке размещается продольное ребро постоянной высоты hr и нулевой толщины. На ребре, подобно твёрдой нижней стенке, обеспечивается выполнение условий прилипания и сохранения нулевой температуры. При этом сетка в направлении z берётся неравномерная, со сгущением вблизи ребра. Выполнение условий непротекания на ребре обеспечивается путём применения алгоритма погружённых границ [4], согласно которому в правые части уравнений Навье–Стокса добавляются искусственные силы, стремящиеся на каждом шаге численного интегрирования остановить поперечное движение частиц жидкости. Условие непротекания выполняется в этом случае не точно, а с погрешностью O (А2) (At — временной шаг), что ограничивает величину At. Как показывают выполненные вычисления, ограничения эти в большинстве случаев не являются чрезмерно обременительными.

При рассмотрении пространственно неоднородных течений в данной работе качественно моделируется течение в канале переменной высоты: H ( x ) = h ( 1 -у cos ( 2 n x )/ L x ) . Здесь у — параметр, задающий степень неоднородности высоты канала. Поскольку в несжимаемой жидкости расход Q в любом поперечном сечении канала постоянен, то отвечающая этому сечению средняя скорость U b = Q/H равняется U b ( x ) = u b h[H ( x ) , где u b = Q/h — средняя скорость в прямом канале, которая считается заданной. Для упрощения вычислений расчётная область остаётся прямоугольной, а изменение средней скорости вдоль канала обеспечивается путём периодического по длине вдува/отсоса, то есть за счёт ненулевого значения нормальной скорости V b ( x ) на границе y = h . Для сохранения условия несжимаемости принимается, что V b ( x ) = - hdU b/ dx . Следуя [5], принимается отсутствие касательных компонент завихрённости на поверхности y = h . С учётом вышесказанного граничные условия при y = h приобретают следующий вид:

5 u _ 5 v

5 y   d x ’

^v = V b ( ^x ) ,     | w = 0.

d y

Для численного решения задачи применялся универсальный метод решения уравнений Навье–Стокса [6], использующий конечно-разностную дискретизацию по пространственным координатам и полунеявную схему интегрирования по времени. В данной работе представляются результаты, полученные при следующих значениях параметров: число Рейнольдса Re = u b h/ и = 2800 , число Прандтля Pr = и/а = 1, длина расчётной области (продольный период) L x = 36 h , ширина расчётной области (поперечный период) L z = 3 h , высота ребра h r = 0.2 h , параметр неоднородности высоты канала у = 0.2 . Число узлов расчётной сетки составляло 512 x 64 x 128 в направлениях x , y , z , соответственно.

• 3.    Результаты расчётов

  • 3.1.    Течение с постоянной по длине канала средней скоростью

    Покажем результаты, демонстрирующие точность и надёжность расчёта турбулентного течения в базовом канале, то есть в канале с гладкой стенкой и постоянным вдоль канала расходом. Результаты настоящей работы сравниваются с результатами [7], полученными при том же числе Рейнольдса. Подробные данные из [7] имеются в Интернете (см. [8]). Несмотря на то, что в настоящей работе используются искусственные условия симметрии при y = h , результаты двух расчётов близки. В частности, коэффициенты сопротивления С у = 2 т w Дрu 2 ) ( т _w — среднее трение на стенке, р — плотность жидкости), составляют 0.008049 и 0.008136, то есть различаются на 1.0%.

На рисунке 1 приведены профили средней скорости U ( y ) = ( u / и профили среднеквадратичных пульсаций продольной скорости u '( y ) = (^ u ²^ - U ² ) (угловые скобки означают осреднение по времени), полученные в [7] и в настоящей работе. В силу однородности течения в направлениях x и z средние характеристики зависят лишь от одной координаты — y . Здесь и далее все величины представляются в безразмерном виде. В качестве масштабов берутся высота канала h , средняя расходная скорость u_b и средняя по объёму температура T_b . Профили средней скорости в двух расчётах совпадают с графической точностью. Так же близки и профили пульсаций скорости. На рисунке также показаны профили средней температуры T ( y ) = (0) и профили среднеквадратичной интенсивности пульсаций температуры T '( y ) = ( (О ² ^ - T ² ) . При выбранном числе Прандтля Pr = 1 и используемой постановке соответствующие температурные и скоростные характеристики близки, что облегчает изучение их изменения под влиянием тех или иных внешних факторов, рассматриваемых ниже. Для сопоставления интенсивности теплообмена с величиной пристенного трения удобно пользоваться безразмерным числом Стэнтона, которое по аналогии с коэффициентом сопротивления определим как St₂ = 2 q w Дu_bT_b ) , где q w = а ( dT/dy )| . Число St₂ вдвое

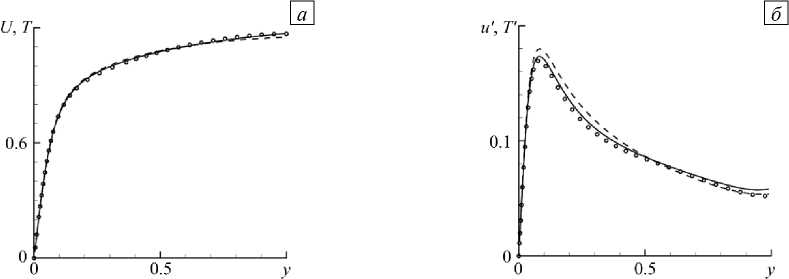
Рис. 1. Профили средней скорости U (сплошная линия), температуры T (штриховая линия), профиль скорости согласно [7] (символы) ( а ); профили среднеквадратичных пульсаций продольной компоненты скорости u ' (сплошная линия), температуры T ' (штриховая линия), профиль среднеквадратичных пульсаций продольной компоненты скорости из [7] (символы) ( б )

превышает традиционно определяемое число Стэнтона St и лучше подходит для оценки степени выполнения аналогии Рейнольдса, которая в случае Pr = 1 приобретает вид: St2 ® Су . В случае гладкого канала имеем St2 = 0.008156, то есть коэффициент аналогии Рейнольдса CR = St2/Су имеет близкое к 1 значение 1.013.

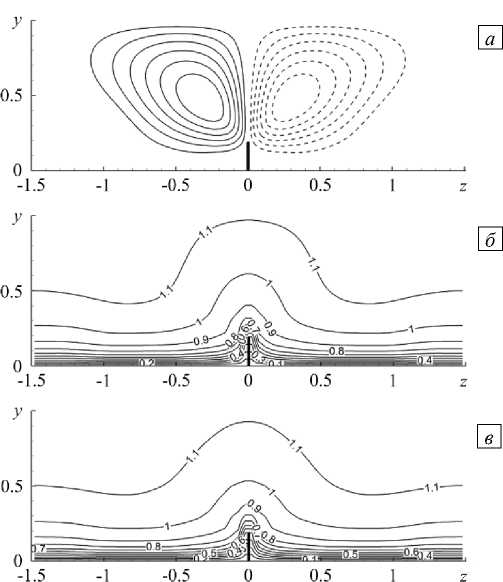
Рис. 2. Линии тока вторичного течения ( а ) (сплошные линии тока отвечают движению жидкости против часовой стрелки, штриховые – по часовой стрелке); распределения по поперечному сечению канала средних значений продольной компоненты скорости ( б ) и температуры ( в )

аналогии Рейнольдса сохраняет своё значение на уровне

Размещение продольного ребра на нижней стенке канала порождает в турбулентном потоке вторичное течение Прандтля 2-го рода [1]. В среднем течении (которое теперь зависит от двух координат: y и z ), кроме продольной компоненты скорости, появляются и поперечные компоненты. Линии тока вторичного течения изображены на рисунке 2 а . Над ребром скорость вторичного течения направлена вверх, а вдоль нижней стенки — по направлению к ребру. Скорость вторичного течения достигает в данном случае 5.2% от u_b . Движение в поперечной плоскости вызывает значительные искажения в распределениях скорости и температуры по сечению канала (Рис. 2 б , в ). Благодаря наличию вертикального движения жидкости над ребром изолинии скорости и температуры приобретают характерные выпуклости, направленные вверх. Как и в гладком канале, распределения средней скорости и температуры по сечению канала близки между собой. Так же близкими оказываются значения коэффициентов C_f и

St2 . Трение и поток тепла на стенке канала уменьшаются примерно на 1% (течение замедляется вблизи основания ребра), но увеличиваются (примерно на 11%) за счёт трения и теплообмена непосредственно на поверхности ребра. В целом коэффициент 1.01. Таким образом, в рассмотренном случае наличие продольного ребра не приводит к заметному изменению теплогидравлических характеристик обтекаемой поверхности. Напомним, что никаких оптимизационных поисков ни по форме, ни по размеру ребра в этой работе не проводилось.

• 3.2.    Течение в канале с переменной по длине средней скоростью

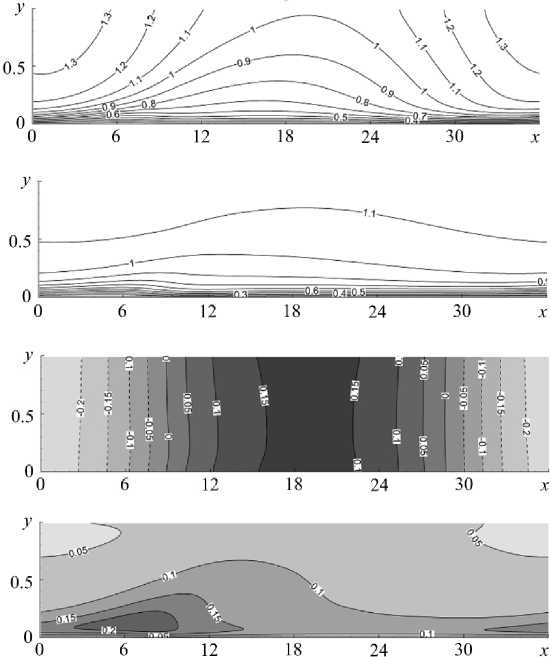
Течение с переменной по длине канала средней расходной скоростью моделируется путём организации вдува/отсоса жидкости через верхнюю стенку, как было сформулировано выше. Средние характеристики турбулентного течения в такой постановке зависят от координат x и y . На рисунке 3 представлены поля средних по времени продольной компоненты скорости U , температуры T , давления P и среднеквадратичной интенсивности пульсаций продольной скорости u' . Из поля давления вычтена линейная по x составляющая, обеспечивающая прокачку жидкости с заданной постоянной средней скоростью иь. Средняя по сечению скорость течения Ub (x) меняется в пределах от 0.81 до 1.23, но сохраняет среднее по всей длине канала значение, равное 1.0. В первой половине канала скорость отсоса жидкости положительна, в результате Ub (x) уменьшается, а во второй — скорость отсоса отрицательна (что соответствует вдуву), и Ub (x) увеличивается. С изменением Ub (x) происходят серьёзные изменения в распределение U (x, у) (см. Рис. 3а), по сравнению с однородным по x распределением при отсутствии вдува/отсоса. Воздействие вдува/отсоса сказывается и на распределении температуры (см. Рис. 3б), однако температура менее чувствительна к нему, чем продольная компонента скорости. Периодическое поведение Ub (x) приводит к изменению давления. В соответствии с законом Бернулли уменьшение скорости сопровождается увеличением давления и наоборот, так что максимальное давление достигается на середине длины канала, где Ub имеет минимум. При всех x распределение среднего давления почти постоянно вдоль вертикальной координаты y .

а

б

в

Рис. 3. Течение с переменной по длине канала средней скоростью; изолинии средних полей параметров в плоскости ( x , у ) : продольной компоненты скорости ( а ), температуры ( б ), давления ( в ), интенсивности пульсаций продольной скорости ( г )

На первой половине длины канала жидкость движется в условиях неблагоприятного градиента давления (сила давления действует навстречу потоку). Такая ситуация служит причиной возникновения точек перегиба в профилях скорости, что отражается, в частности, в появлении повышенного уровня турбулентных пульсаций и ' в этой области (см. Рис. 3 г ). Максимум и ' = 0.24, достигающийся при у = 0.12 и x = 7, вдвое превышает минимальное значение u ' на этой высоте. В этой же области наблюдаются и максимальные пульсации температуры (на Рис. 3 не показаны), хотя вариация их интенсивности по длине канала на этой высоте незначительна: от 0.17 до 0.19.

Изменения в характеристиках турбулентности, по сравнению с аналогичными характеристиками в однородном по длине канала течении, отражаются на теплогидравлических свойствах течения. Так, коэффициент сопротивления меняется противоположно: на участке увеличения средней скорости (на первой половине канала) Cf уменьшается на 19%, а на второй половине канала увеличивается на 24%. Суммарно получается рост Cf на 2.6%. Число Стэнтона повышается на обоих участках практически в равной степени — на 9%. В результате коэффициент аналогии Рейнольдса достигает значения CR = 1.07 , что на 6% больше, чем в однородном канале.

Размещение продольного ребра на нижней стенке, так же, как и в однородном канале, вызывает появление вторичного течения, характеризующегося циркуляционным движением жидкости в плоскости, перпендикулярной направлению основного течения. Вторичные течения в турбулентном потоке возникают под действием напряжений Рейнольдса, которые, в свою очередь, пропорциональны интенсивности турбулентных пульсаций. Увеличение интенсивности пульсационного движения на участке замедления потока ожидаемо приводят к усилению вторичных течений, характерная скорость которых на этом участке вырастает на треть, по сравнению с однородным каналом. Оребрение канала практически не влияет на итоговое значение коэффициента аналогии Рейнольдса. Как и в однородном по x канале, незначительно (на уровне 1%) уменьшаются трение и теплообмен на стенке канала и более заметной (более 10% в каждом случае) становится добавка за счёт трения и теплообмена непосредственно на поверхности ребра. Таким образом, по сравнению с однородным каналом с гладкой стенкой, повышаются и коэффициент трения (на 14.2%), и число Стэнтона (на 20.3%). При этом коэффициент аналогии Рейнольдса равняется C_R = 1.07 , что совпадает со значением в неоднородном канале с гладкой стенкой.

4.    Заключение

Проведено численное исследование турбулентного течения в плоском канале. Побудительным мотивом данного исследования стал результат работы [2], где обнаружен эффект опережающего роста конвективного теплообмена, по сравнению с ростом трения, в присутствии вторичных течений, создаваемых продольным оребрением стенок канала. Цель работы заключалась в изучении особенностей вторичных течений Прандтля 2-го рода, возникающих в окрестности продольных рёбер, в условиях пространственной неоднородности потока. Проведены расчёты четырёх турбулентных течений: течения в однородном по длине гладком канале, однородном оребрённом канале, а также течений в гладком и оребрённом каналах с изменяющейся по длине средней скоростью. Температура рассматривается как пассивная примесь, влиянием термических эффектов на поле скорости пренебрегается. В работе не проводились оптимизационные исследования, направленные на варьирование геометрии, расположения и высоты рёбер. Целью было выявление качественных закономерностей с фиксированным по форме и размеру ребром. Обнаружено, что наличие ребра в однородном канале значительно меняет распределения характеристик турбулентного течения по сечению канала. Эти изменения обусловлены действием возникающего вторичного течения с максимальной скоростью в 5.2% от средней расходной скорости потока. При этом изменения в скоростных и тепловых характеристиках оказываются подобными. Как трение, так и теплообмен увеличиваются примерно на 10% благодаря расширению площади смачиваемой поверхности. Коэффициент аналогии Рейнольдса, характеризующий теплогидравлические свойства канала, сохраняет постоянное значение на уровне 1.01.

Неоднородность потока, которая обеспечивается организацией вдува и отсоса через верхнюю стенку канала, приводит к более заметным изменениям. На участках замедления потока жидкость движется в условиях неблагоприятного градиента давления (сила давления направлена навстречу потоку). В этих условиях профили скорости в пристенной области имеют точки перегиба. Интенсивность турбулентных пульсаций в этих местах заметно возрастает. При наличии оребрения это приводит к существенному усилению вторичных течений. Пристенное трение и теплообмен в условиях пространственной неоднородности ведут себя по-разному. На участке замедления потока трение падает, а на участке ускорения — возрастает. При этом интенсивность теплообмена на стенке практически не реагирует на изменение средней скорости, на обоих участках наблюдается повышение теплообмена. Наличие ребра не приводит к качественным изменениям: как трение, так и теплообмен увеличиваются одинаково. Как в гладком, так и в оребрённом канале зафиксировано повышение коэффициента аналогии Рейнольдса до значения 1.07, что на 6% выше показателя в однородном течении.

В целом по результатам настоящей работы можно сделать вывод, что продольное оребрение, вызывающее вторичное течение в поперечной к потоку плоскости, само по себе едва ли способно существенно изменять теплогидравлические свойства плоской поверхности в турбулентном потоке, по крайней мере, без принятия специальных оптимизационных мер. Пространственная неоднородность потока, наоборот, в силу разного воздействия на распределения скорости и температуры имеет определённый потенциал для конструирования теплообменных устройств с более подходящими теплогидравлическими свойствами.

Работа выполнена при финансовой поддержке РНФ в рамках научного проекта № 22-21-00184, с использованием вычислительных ресурсов ОВК НИЦ «Курчатовский институт»,