Введение в классическую мезодинамику связанных нуклонов

Математический аппарат НСО можно использовать в задачах, которые на первый взгляд не имеют никакого отношения к системам отсчета, однако в действительности эти задачи оказываются тесно связанными. К таким задачам относятся, например, расчеты электростатических и мезонных полей связанных (несвободных) зарядов. [1], [2], [3], [4].

В классической электродинамике принято считать, что если точечный заряд покоится в некоторой ИСО, то его электрическое поле является кулоновым вне зависимости от того, является ли этот заряд свободным или сумма сил, действующих на заряд, равна нулю. Например, поле свободного точечного заряда и поле точечного заряда, подвешенного на нити в однородном поле, в плоском пространстве - времени считаются одинаковыми и изотропными. С другой стороны, для равноускоренного заряда электрическое поле в сопутствующей НСО не является изотропным, как не является изотропным и поле заряда, подвешенного на нити в поле тяжести. Поэтому возникает естественный вопрос: почему поле заряда Q, подвешенного на нити в электрическом поле, изотропно, а поле этого заряда, находящегося в эквивалентных условиях в НСО или поле тяжести, неизотропно?

На первый взгляд ответ ответ кажется очевидным. Поля сил тяжести и сил инерции имеют близкую природу и эти поля взаимодействуют как с заряженными, так и нейтральными частицами и их полями. По этой причине поле точечного электрического заряда, закрепленного в ньютоновом гравитационном поле или в НСО, перестает быть сферически симметричным. В силу линейности уравнений Максвелла внешнее электрическое поле, в котором закрепляется точечный заряд, не взаимодействует с полем этого заряда, поэтому симметрия поля точечного заряда должна сохраняться. В этом ответе есть маленькая некорректность, которая противоречит экспериментальным данным при рассеянии “света на свете” [5]. Данная проблема возникла в связи с открытием позитрона и образования пар, то есть одновременного возникновения электрона и позитрона под действием жестких ү - лучей. Линейные уравнения Максвелла в принципе не могли привести к такому рассеянию, что непосредственно следует из принципа суперпозиции полей. Две волны должны были проникнуть одна через другую. Поэтому эксперимент требует некоторого изменения уравнений Максвелла в сторону их нелинейности. По этой причине должно быть взаимодействие электрических полей, собственного поля закрепленного в электрическом поле заряда с внешним полем. Это должно привести к отсутствию сферической симметрии закрепленного во внешнем поле точечного заряда.

С нашей точки зрения поле точечного заряда, подвешенного на нити, эквивалентно полю этого заряда в сопутствующей НСО dS2 = exp(2a0y1/c)(dy0)2 - (dy1)2 - (dy2)2 - (dy3)2.

( * )

rqe ускорение a° направлено вдоль осп y¹ [G]. В равтіоускоретшост 口 НСО (*) можно убедиться непосредственно

DV¹ — ^dV¹ 1 厶 /0 、 2 — 1 р 1 _ g^{11 d}g00 — ao 而 =lš+l⁰⁰l^V = 麻 1⁰⁰ = —而 9 = 戸 .

( ** )

Остальные компоненты 4-ускорения равны нулю. a°, направлено параллельно силе натяжения пит ii ^Т. действутотттеп на ， заря 】, ііііыміі словами мы полагаем, что поле точечного заряда подвешенного на нити в однородном электростатическом поле, будет таким же, если заряд двигать ускоренно вне поля, сохраняя прежней значение силы натяжения нити. В обоих случаях физическая ситуация для заряда будет очевидно одинаковой, что и должно приводить к тождественности полей.

На основании сказанного сформулируем

Постулат эквивалентных ситуаций. Поле точечного заряда, находящегося в равновесии в постоянном электрическом поле, эквивалентно полю от этого заряда в равноускоренной НСО, если силы реакции связей, ускоряющие заряд и удерживающие заряд в поле неподвижным, равны |6].

Физический смысл постулата состоит в том, что внешнее поле действует не только на заряд (источник поля), но также и на его ближайшее окружение, то есть поле заряда. Это приводит к нелинейности уравнений Максвелла в малой области вокруг пробного заряда, что и подтверждается экспериментом при рождении пары электрон - позитрон. Так как связь препятствует заряду двигаться, то окружающее этот заряд его собственное поле деформируется, что должно привести (далее будет показано, что это так и есть) к возрастанию uфизичecкoй^^ напряженности собственного поля заряда в направлении обратном силе реакции. Этот постулат мы распространяем и на другие поля.

1.    Скалярные ядерные силы связанных нуклонов

Рассмотрим сначала простейший вариант теории ядерных сил, основанный на допущении, что сила притяжения между любыми нуклонами обуславливается нейтральным мезонным полем, которое определяется одііокомпоііеіітпой скалярной вещественной функцией “. Теорию скалярных ядерных сил будем строить в рамках классической (неквантовой) мезодинамики, с учетом “связанности” поверхностных нуклонов в ядре. Будем считать для простоты модели, что как и для заряженных проводников, нуклоны, которые находятся на поверхности ядра, взаимодействуют с создаваемым ими внешним полем. Ввиду короткодействия ядерных сил, нуклоны расположенные в объеме ядра, с внешним полем вне ядра не взаимодействуют, а взаимодействуют лишь с ближайшими соседями. Однако конкретное распределение нуклонной плотности в ядре на первом этапе учитывать не будем, так как учет распределения плотности нуклонов в ядре (как и учет распределения плотности заряда внутри электрона в теории электромагнитной массы) не приведет к существенному эффекту. Существенным отличием ядерных сил от электромагнитных является сила притяжения между одинаковыми нуклонами, вместо силы отталкивания между одноименными зарядами в электродинамике. Это приводит к тому, что нуклоны на поверхности ядра испытывают силу положительного давления со стороны создаваемого ими поля (вместо силы отрицательного давления со стороны электрического поля заряженного проводника.) Так как каждый из нуклонов покоится, то сила со стороны поля уравновешивается силой связи со стороны ядра. С нашей точки зрения каждый из нуклонов на поверхности ядра в силу постулата эквивалентных ситуаций, который мы распространяем и на ядерные силы, ^движется55 ускоренно по радиусу от центра. Итак, каждый из нуклонов на поверхности ядра, которое считаем сферическим по форме, эквивалентен размещению в начале координат некоторой равноускоренной НСО с метрикой (*). Так как в метрике (*) пространственное сечение является плоским, то вклад в скалярный потенциал ^ от всей сферы можно вычислить путем интегрирования вклада от элементарных “зарядов” каждого из элементов сферы в плоском пространстве ( но в римановом пространстве - времени).

Поэтому предварительно возникает задача о нахождении поля нуклона в равноускоренной НСО.

Так как физические законы должны быть справедливы во всех СО, значит они должны выражаться в виде тензорных уравнений. Если уравнения содержат производные полевых величин, то это должны быть ковариантные производные. Следовательно, известные уравнения скалярного мезонного поля, создаваемого точечными нуклонами, имеющие в ИСО вид [7]

卜2- c12 d2 -k2)也= 4n，g‘s (戸-r⑴), где1 g‘ - мезонныіі 'заряд, f’(t) - радиус-вектор движушегося нуклона, должны быть в НСО представлены в форме

-g*^vV_MVv3 - k23 = 4ng 華 (f - Г (t)),

,2n

k0 =7~

h

В соотношении (2) 〃 - масса нуклона, h - постоянная Планка, f - радиус-вектор координаты точки паблтодеипя. g*^v - метрпческііп тензор НСО. Напіісаііііое уравнение (2) носит название уравнения Клейна - Гордона. Уравнение можно преобразовать к другому виду, используя известное соотношение для ковариантной дивергенции произвольного векторного поля V/ = A* в виде

∇ µA^µ

1 d ( CA")

√-g   ∂yµ

⑶

Из (3), находим для (2) выражение

7b. (rg^g“^V 言) ^-k²³ = 4^ngs ( 戸 ^-r^(t)) •

Чтобы решить уравнение (4) необходимо знать компоненты метрического тензора g^. В равноускоренной НСО метрика определена из соотношения (*). Будем искать стационарное решение (4) с учетом метрики (*), считая, что точечный нуклон расположен в начале координат. В результате приходим к следующему уравнению

△ ³ + a⁰ 祟- k23 = 4ng'6(y¹)5(y²)5(y³).

c2 ∂y1

Решение (5) ищем в виде

3 = u ( y¹, y², y³ ) exp ( ly¹ ) , A = - a = - 2C02.

После чего уравнение для u сведется к форме

△u - (a4 + k2) u = 4ng‘ exp (号)s (y1) S (y2) S (y3), а его решение u = -g"exp (-r jk2 +     -

⑸

⑹

⑺

⑻

Отметим, что хотя пространство (*) - риманово, но его пространственное сечение евклидово, в котором существует радиус - вектор. Из рассмотренного следует, что решение уравнения (5) имеет вид

ψ

- д’    [- a0r ( «1 + r P I

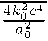
+ cos Ө )

2c2

.

⑼

Решив предварительную задачу о поле нуклона в равноускоренной НСО, приступим к решению основной задачи нахождению поля ядра, учитывая, что поверхностные нуклоны в ядре находятся в особом состоянии, эквивалентном их “ускоренному движению” по радиусу от центра.

Разобьем поверхность сферического ядра на элементарные ячейки, выбрав сферическую систему координат с началом в центре ядра. На поверхности ядра естественным образом возникают аффинные ортогональные реперы с векторами, направленными вдоль координатных линий. Выберем на полярной оси вне ядра некоторую точку наблюдения, в которой вычислим ядерный потенциал от поверхностных нуклонов ядра. Введем нуклонную поверхностную плотность зарядов а. Из соображений симметрии очевидно. ^т-гто для лтобого полярного угла Ө. отст-штываемого от полярной оси, вклад в ядерный потенциал от элемента в точке наблюдения не зависит от азимутального угла ф. Поэтому вклад в потенциал 亜 ^от кольца ширины Rd 。 и радиуса R sin Ө имеет

вид

-     2naR² sin Ө        a⁰r' ( ， ¹ + ^4k02c" + ^{cos ү})

琳 =--r— exP--2c2......

dθ.

Зд ( ?сь ү - угол мс'жду ра,"ціусом-вектором из начала координат до 'Элемента 'заряда и радиусом-вектором Г* от 'Элемента 'заряда до точки ііаблтодеішя.

Отметим во избежание недоразумений, что с точки зрения локального наблюдателя, связанного с элементом поверхности, на которой расположен “ускоренный” нуклонный заряд, пространство является плоским, а пространство-время — римановым. Поэтому Г* и 戸 с точки зрения этого наблюдателя имеют ясный геометрический смысл. С другой стороны, совокупность мировых линий частиц, расположенных на сфере, с точки зрения глобального наблюдателя, находящегося в начале сферической системы отсчета, не принадлежит жесткой равноускоренной НСО, поскольку радиальные ускорения не параллельны. Для такого наблюдателя совокупность рассмотренных мировых линий частиц на сфере принадлежит к радиальноускоренной жесткой НС О. “Пространственное сечение⁵⁵ для частиц на сфере не будет плоским.

Так как с точки зрения наблюдателя на элементе поверхности сферы трехмерное пространство плоское, то, используя элементарные тригонометрические преобразования, получим для ядерного потенциала ^ выражение

也二- g.евгр - ^exp ( -屮 + ^x)) d,. ( ii )

Здесь введены следующие обозначения

x = cos Ө,

/ 、｝ ,

p

R r

b = д/1 + a² - 2ax.

Интеграл (11) можно преобразовать к виду

g‘                                   SO-P ( l + ^f))

^ = 后 exp ( - s² + s²p²(1 - f²)) /           exp(u²)du,

2Rs                              s(i+p(i-f))

где величина s определяется равенством

s

βr

2p = rV

a0

4Rc2 '

Потенциал ^ скалярного Аіезошюго поля можно найти ii ііепосредствеішо из решения уравнения (4) с нулевой правой частью, выбрав стационарное решение для случая сферической симметрии. Компоненты метрического тензора задаются интервалом dS2 = exp(v)(dy0)2 - r2(dӨ2 + sin2 Өdф2) - exp(A)(dr)2,                  (* * *)

rje V ii А ^зависят только от r (***[ в котором (функции v(r) ii A(r) требуется определить. Из (4) получаем соотношение д 卜xp    ) r2 奈)=吟(r) exp (雯)•

Соотношение (15) при известной функции ^(r) из (13) связывает искомые функции v(r) и А(г).

Для нахождения второго уравнения, связывающего эти функции, рассмотрим силу со стороны поля, действующую на “пробный" нуклонный “заряд^ g‘, закрепленный в точке с координатой r от центра шара. Пусть масса пробного заряда m°. Тогда вектор первой кривизны F1 мировой линии этого заряда можно найти из соотношения

弓=V v Vv以, записав для закрепленных зарядов условие сопутствия для метрики (***) в виде

V k = 吸 = 0,V⁰ = (g00 ) T/²,

V0 = (g00 ) 1^/2 ,F1 = F (r) ,F⁰ = F² = F³ = 0.                        (16)

Откуда из [10, формулы (1.5), (19.4)] и (16) имеем

F1 = 2dr exp(-A).                                    (17)

С другой стороны, эту величину можно найти и из силы, действующей на нуклон со стороны связи, удерживающей нуклон в поле неподвижным. Эта сила численно равна силе со стороны поля и противоположна ей по знаку. Уравнения движения нуклонного заряда в скалярном мезонном поле можно найти из закона Ньютона, представимого в виде

DV µ dS

為(产 ^-V " ”) dyV

В нерелятивистском приближении эта формула совпадает с обычным уравнением движения нуклона в скалярном мезонном поле [7].

В согласии со сказанным выше, получаем формулу

¹ dr exp(—^A) = -g^ exp(^-A) 第 2 dr            m°c²          dr

из которой, с учетом обращения метрики на бесконечности в плоскую, имеем

V (r) = 2 ^g =(r).

m0c2

Итак, формулы (20), (13) определяют goo компоненту метрического тензора скалярного мезонного поля. Компоненту gn метрического тензора можно определить из уравнения (15), которое можно представить в следующей форме:

dr + h(r) Y (r) = k(r) ,Y (r) = exp (-А), h (r) = T dr,

T(r)=eXP ( 2 )『2 дГ k (r) = 2# ∂r

Таким образом, получили линейное неоднородное уравнение, решение которого представимо в виде:

Y (r) = exp (—/ h (r) dr) / exp (/ h (r) dr) k (r) dr+

+C exp

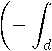
r h (r) dr 1 .

Решение уравнения представлено здесь как сумма двух функций. Первая при r = d обращается в нуль, а вторая принимает значение C. Внутренний интеграл легко берется в квадратурах.

/ h (r) dr = In

откуда следует выражение

^Y(r) = 為 /^exp(v)r4 噂 ^dr+C (需) .

В соотношении (23) интегральная кривая Y(r) проходит через точку (d, C). Считая, что на бесконечности метрика является плоской, получим

Y (r)

( 必 Y 「— 2k2 厂

T(r)         T2(x) J r

exp(v)r4 也学 dr]. ∂r

Формулы (13), (20) и (24) определяют геометрию пространства - времени скалярного мезонного поля. Зная метрику и скалярный потенциал ^, найдем тензор энергии-импульса нейтрального скалярного поля, воспользуясь результатом работы [8]. В результате получаем

—n ( дф дф 1  2 _ н" = 4П 砲 dyv 十 2 I 0 -

∂ψ ∂ψ ∂yλ ∂yλ

gµν .

Зд ( ?сь n - размерная постоянная, выбор которой ^зависит от конкретного вида скалярного поля. Для интересующей нас тетрадной компоненты Т ( о)(о) тензора энергии-импульса получаем выражение

T(0)(0)

n ^dфdф , ¹ 厶 2 4n dSdS ⁺ 2 V⁰ -

∂ψ ∂ψ ∂yλ ∂yλ

))

Для стационарного случая в сопутствующей системе (16) находим

n 2 2 kl ∂ψ ∂ψ

^T(0)(0) = 8П (.k^0ф - g dyk dyi 丿.

Далее, воспользуясь общей формулой для энергии поля, получим выражение w = / t (0)(0) v-gd3y n        A + V、

=šnj ^exp(^Т 丿

r2 sin Ө 卜2ф2 十 e-'(字))dӨdфdr n /exp (千)r2 卜詠2+ef (dr)) dr.

Воспользуясь уравнением (15), имеем для первого члена в (28) выражение n / exp (A十■上)r2k2ф

2 _dr

n ∂ ν - λ ∂ψ

=2/也加(口р丁)Г/)dr， которое после интегрирования по частям сводит энергию поля W к виду W = - 2也(R)exp ( V(R)2 “(R)) R*"

Отметим, что полученные результаты неоднозначны. Уравнение (2), как известно, например, из [9], зависит от метода вывода и может быть представлено в следующей форме

—g*vVMVv3 — k証一kR^ = 4ng'B (戸一Г (t)), ko

2n^c h

.

Зд ( ?сь R - скалярная кривизна, k - некоторая постоянная. зашісяш,ая от способа получения второ уравнения. Мы не будем на этом останавливаться, отсылая читателя к работе [9].

2.    Скалярная ньютонова гравитационная сила связанных масс

Проведем анализ полученного соотношения для энергии поля.

Для частного случая ko = 0, нейтральное мезонное поле по структуре напоминает ньютоновское гравитационное поле. Решим следующую задачу.

Пусть имеется невесомая твердая оболочка радиуса R, окруженная взаимодействующими друг с другом по закону всемирного тяготения Ньютона частицами пыли. Пусть массивные пылинки расположены в очень тонком сферическом слое, толщина которого пренебрежимо мала по сравнению с радиусом оболочки. Ясно, что под действием силы взаимного притяжения частицы будут давить на оболочку. По третьему закону Ньютона оболочка будет давить на частицы, вызывая у них появление “ускорения”, направленного от центра оболочки по радиусу. В согласии с постулатом эквивалентных ситуаций и вычислениями, проведенными в предыдущем разделе, потенциал скалярного гравитационного поля гравитирующего слоя можно получить из формулы (13), полагая в ней f = 1.

3 = 备 exp(—s²) /      exp(u ²)du,                        (32)

2Rs           s где величина s определяется равенством

s

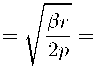
r ao 4Rc2 '

В согласии с принципом соответствия, при исчезающе малых значениях s должно получаться выражение для ньютонова потенциала. Откуда следует, что заряд g‘ = kM, где k - гравитационная постоянная. M - масса всех частиті в слое. Величина а° на поверхности оболочки равна ， половине от величины ускорения свободного падения пробных частиц на оболочку, что дает для s

r s = 4R

,

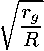
2kM

『g = h, где1 Гд - гра.вптатцюппып радиус.

Для скалярного гравитационного поля уравнение (15) сводится к виду дг 卜xp (吋卜2 dг) = 0,

интегрируя которое при выполнении принципа соответствия, получаем exp (亏

斗 2 9±

∂r

kM.

Воспользуясь выражением для энергии (30), получим

n

W = — 2 k“(R).

Если мы пренебрежем “ускорением” частиц на сфере, то в силу классического соотношения kM

9=- 丁， получаемого из (32) при s т 0, находим

W

n k²M²

2 R

Из принципа соответствия для ньютоновского гравитационного поля выбираем

после чего выражение для энергии поля вне оболочки в нулевом приближении совпадает с ньюто новским аналогом.

W

1 kM ²

2 R

Знак минус говорит о том, что массы в гравитации всегда притягиваются. В электростатике одноименные заряды отталкиваются, поэтому электростатическая энергия заряженного шара для заряда любого знака положительна.

Отметим, что рассматриваемая нами ньютоновская скалярная гравитация рассматривается в римановом пространстве-времени. Она ни в коем случае не претендует на замену ОТО и представляет чисто методический интерес, как некоторый частный случай безмассового мезонного скалярного поля, для которого уравнения более просты, чем для массивных мезонов.

Из формулы (40) следует, что при R т 0 энергия гравитационного поля оболочки при фиксированной массе M стремится к минус бесконечности. Это вполне естественно для теории Кулона и Ньютона и является главной трудностью этих теорий.

Найдем значение энергии скалярного гравитационного поля в нашем случае. Для этого воспользуемся выражениями (37) и (32) при p = 1. В результате получим

帆 R) = - g^—^ 卜叫

s(R) = 8

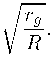
При R т 0- 8 т а* поэтому исполь ： зуя (формулу [10. (19.22)]. находим

W = —2Mc2.

Знак минус в энергии означает наличие притяжения между частицами, а удвоение энергии обусловлено наличием давления Пуанкаре со стороны жесткой оболочки на частицы.

3.    Энергия протона

При рассмотрении электромагнитной энергии электрона для устранения его взрыва под действием кулоновских сил было необходимо вводить поверхностное давление Пуанкаре [5] . Природа этого давления неизвестна, однако оно необходимо для объяснения устойчивости электрона. При рассмотрении протона давление Пуанкаре обусловлено естественными ядерными силами. Для простоты будем считать, что заряд протона размазан по его поверхности, а отрицательное давление со стороны созданного протоном электромагнитного поля удерживает протон от коллапса. Таким образом, сила со стороны электромагнитного поля играет роль связи для противодействия основным ядерным силам сжатия. Эти силы, направленные по радиусу от центра протона, аналогичны силам реакции “опоры”, противоположны по знаку силам Пуанкаре для электрона, и, в отличие от сил Пуанкаре, вызывают положительное “ускорение” для элементов зарядов на поверхности протона. Поэтому для вычисления энергии протона будем использовать формулу (19.3) из [10] вместо соотношения (19.3а) из [10], которое использовалось нами ранее

Ao = Q ^eX pf 2 ) [Ф(С(1 + 2R/r)) - Ф(0

(19.3)

ζ

Rr

eQ 8mc2R

Ao = Q 吗— ^Z 2 ) ⁷ⁿ i [Ф(іС (1 - 2R/r)) - Ф(с0

(19.3a)

В [10, формулы (19.3), (19.3а)] Ao - нулевая компонеита 4-потенциала, r - расстояние от центра шара до точки наблюдения, Ф(《)-интеграл вероятности, Ф(і《)-интеграл вероятности мнимого аргумента.

ф(0

π0

exp(-t2) dt

ф(іО

今｛ exp(t2 ) dt

ierfi(Z).

Дальнейшее вычисление электростатической энергии протона производится по формулам раздела 19 из [10] с положительным “ускорением” и для протона приводит к соотношению [10, формула (19.23)] с N=1, то есть

Ao(R) ~

謠( ^{1 -} 2y

2mc2

丁 ^1-

4mc2R eQ

)

爪=QA0 = Nmc2(r _mC2R^\ 2                 e2N

(Откуда, при R т 0 имеем

W = Nmc2,

(19.23)

W = mpc² (1 -修),

где¹ mp - масса покоя протона, а R - его характерный размер. Последняя 巾 ор мул а с пр аве, if ів а ； когда параметр 8 в [10, формула (19.8)] много больше единицы, что эквивалентно R т 0. Поэтому для точечного протона его энергия электрического поля

W = mpc2.