Выбор измерительных устройств естественной освещённости, их математических описаний и методик исследования

В статье описаны подходы для решения задач, связанных с уменьшением влияния случайных факторов на результаты измерений.

Объекты и методы исследования

Построение моделей принятия решений и исследование динамического процесса естественной освещённости E(t) проводилось на основе обработки и анализа экспериментальных дискретных значений E(n), полученных с помощью информационно-измерительного устройства в следующем составе: фоторезистивный датчик, модуль текущих интегральных телеизмерений (ТИТ), контроллер, персональный компьютер (ПК).

Схема измерительного комплекса приведена на рис. 1.

Модуль ТИТ Схема енОора

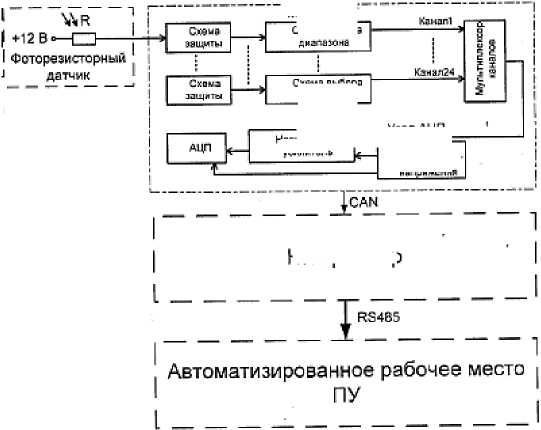
Рис. 1. Схема измерительного комплекса естественной освещённости: АЦП - аналогово-цифровой преобразователь; ПУ - пункт управления

Схема яызсра днапахана

Нормирующий усипитоп»

Узел АЦП

Спорный истаминк нала я мел ни

Контроллер

В качестве датчика был использован фоторезистор ФР764. Подключение производилось таким образом, чтобы ток фоторезисторного датчика был пропорционален уровню естественного освещения. Модуль ТИТ обеспечивает измерение унифицированных сигналов постоянного тока, поступающих на измерительные каналы ТИТ, и передачу обработанных значений измерений по межмодульному интерфейсу CAN. В качестве контроллера применялся модуль МП-03, предназначенный для использования в качестве центрального процессорного устройства для обеспечения в автоматическом режиме сбора, обработки принятой информации, её хранения и передачи результатов измерений в ПУ. Автоматизированное рабочее место, или пункт управления (ПУ), представляет собой персональный компьютер или сервер с установленным программным обеспечением верхнего уровня для связи с контроллером, сбора и сохранения измеренных значений в базе данных. Контроллер и модуль ТИТ являются законченными устройствами, обеспечивающими работу телемеханической автоматизированной системы диспетчерского управления. Таким образом, данные об измеренных значениях тока, пропорционального естественной освещённости, поступают на персональный компьютер (АРМ), где собираются в базу данных SQL. Дальнейшая статистическая обработка производилась используя полученные базы данных.

Результаты исследований

График изменения естественной освещённости, построенный по измеренным значениям E(n) с шагом дискретизации Т, равным пяти минутам, приведён на рис. 2.

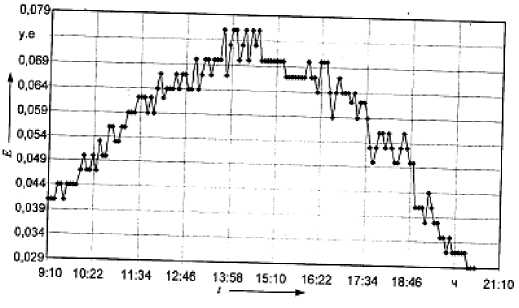
Рис. 2. График освещённости полного сигнала

Анализ построенной зависимости E(t) позволяет выбрать в качестве математической модели процесса изменения естественной освещённости E(t) аддитивную зависимость вида

E(t) = Eo(t) + E(t) .(1)

В выражении (1) под E ₀ ( t ) понимается трендовое изменение освещённости, E ( t )– её случайная составляющая. Аналогичную модель можно записать и для дискретных значений

E(t) = Eo(n) + E(n) .(2)

Статистическая обработка случайных процессов сводится к получению трендовой составляющей E ₀ ( t ) по результатам наблюдаемых значений E ( t ), а затем вычислению случайной E ( t ) по формулам:

E( t) = E (t) - E o( t);(3)

E( t) = E (n ) - E o( n ).(4)

Задача восстановления или определения динамической функции тренда является оцениванием процессов, под которым в математической статистике принято называть обработку данных измерений (наблюдений) с целью уменьшения влияния случайных факторов и ошибок. В настоящее время для решения задач оценивания используются три подхода, а именно:

• •    применение методов оценивания математической статистики;

• •    приближение функций;

• •    фильтрация процессов.

В первой группе при выборе вероятностных критериев оптимизации приходят к методам максимальной апостериорной вероятности или максимального правдоподобия, но в вычислительной практике чаще используется критерий в виде функционалов невязок, или ошибок оценивания, которые приводят к методам наименьших квадратов (МНК), расстояний (МНР), произведений (МНП) и т.д. При обработке случайных процессов в режиме реального времени рекомендуется применять рекуррентные алгоритмы, в частности наиболее популярен рекуррентный метод наименьших квадратов (РМНК).

Во втором подходе оцениваются степени приближения исследуемого динамического процесса к некоторой заданной или выбранной функции. Естественная освещённость E ^~( t ) , как это видно из графика (рис. 2), является периодической, а простейшая колебательная функция – это синусоида. Проверку возможности такого описания тренда E ₀ ( t ) можно осуществить по соответствующей эмпирической гистограмме теоретического закона распределения – арксинуса.

Для подхода, связанного с фильтрацией, разработано достаточно большое число алгоритмов оценивания как непрерывных, так и дискретных процессов, которые различаются типами моделей, применяемых для описания процессов и условий наблюдения, а также вероятностных характеристик случайных сигналов. Если оцениваемый процесс описывается линейным уравнением и наблюдения также линейны, то применяется достаточно известный линейный непрерывный или дискретный фильтр Калмана – Бьюси (ФКБ). Алгоритм состоит из дифференциальных, или разностных, уравнений для вектора восстанавливаемого процесса и ковариационной матрицы ошибок оценивания. В вычислительном отношении такой дискретный ФКБ совпадает с РМНК. Кроме описания процессов во временной области переменных состояния, в теории фильтрации используются и комплексные преобразования, то есть спектры сигналов, позволяющие проектировать и реализовывать достаточно простые аналоговые и цифровые фильтры.

Простейшей операцией, уменьшающей влияние ошибок, является усреднение или, с точки зрения математической статистики, вычисление математического ожидания. Примем следующие обозначения. Допустим, что исследуется непрерывный сигнал u(t) и известны его значения u(n) , полученные из u(t) , с шагом дискретизации Т, а результатом обработки или вычислений являются дискретные величины x(n) . Оценку математического ожидания или среднее значение вычисляют по формуле

1N x (n) = -У u ( n ),                                    (5)

n n = 1

где N – объём обрабатываемой информации или количество измерений.

Выражение (5) можно записать и в рекуррентном виде

x ( n ) = x ( n - 1) + —u ( n ); x (0) = 0, n = 1, N .                             (6)

N

Операция усреднения, или простейшая процедура сглаживания, является частным случаем более общей цифровой фильтрации, описываемой разностным уравнением pq

x ( n ) + У a ( k ) • x ( n - k ) = b (0) • u ( n ) + У b ( k ) • u ( n - k ).

k = 1                                                  k = 1

Если коэффициенты a(k) при k = 1, p и b(k) при k = 1, q - постоянные, то модель (7) и соответствующий цифровой фильтр линейны и можно записать передаточную функцию через коэффициенты в виде

H ( 2 ) =

B ( z ) A ( z )

q b (0) + £ b (k) • 2- k

___________ k = 1 ________________

1 l У a (k) • 2 -k k=1

или через импульсную характеристику

w

H ( 2 ) = £ h ( k ) • 2 — ^k .

k = 0

В частном случае при a(k) = 0 и k = 1, p формулы (8) и (9) определяют выражения передаточной функции qq

H ( 2 ) = B ( 2 ) = У b ( k ) • 2- k = У h ( k ) • 2- * .                           (10)

k = 0                  k = 0

Импульсная характеристика будет конечной и такие цифровые устройства называют КИХ-фильтрами, для них справедливо, что b(k) = h(k), k = 0, q . В общем случае в формулу (9) входит бесконечное число значений h(k) и передаточная функция (8) описывает БИХ-фильтр.

Основной частотной характеристикой является амплитудная, для которой выполняется

I H (, f )|2 = H ( _ •) H ( 2 -1) ₂ = e j- * T .                                   (11)

Частотные характеристики дискретных процессов и систем периодичны частоте дискретизации f 0 = 1/ T , поэтому, как правило, они рассматриваются либо в основной полосе

. f е

^“

Л./ о      .                       n. f o   _т

—;— , либо в полуполосе f е 0;— . Также вводится и нормированная частота

f 0

;2

f при Т = 1, для неё f е [ 0;0,5 ] .

При проектировании сглаживающих фильтров вводится идеальная амплитудная частотная характеристика H _n (^~ f ) , значения которой в полосе пропускания равны единице, а остальные - нулю. Для М значений нормированной частоты f ^ . е [ 0;0,5 ] вводится квадратичный функционал

M

L ( a , b ) = £ | H n ( Z )| - H (f , , a , b ) .

i = 0

и решается задача минимизации

( a , b ) = argmin L ( a , b ).                                          (13)

Как правило, одним из численных методов оптимизации функции L ( a , b ) находят векторы a = | a (1), a (2),..., a ( p )| T и b = | b (1), b (2),..., b ( q )| T .

Можно при проектировании использовать средства автоматизации, так как в состав пакета цифровой обработки Siqnal Processing Toolbox программной системы MATLAB входит процедура yulewalk, осуществляющая расчёт коэффициентов БИХ-фильтра по заданной амплитудной частотной характеристике [1].

Линейные разностные уравнения вида (7) достаточно широко используются и в математической статистике под названием моделей авторегрессии скользящего среднего, или АРСС (p, q), и авторегрессии АР(p).

Простейшими являются модели СС (q) и их коэффициенты b(k), определяющие веса, с которыми учитываются значения входного сигнала u ( n - k ), к = 1, q в формировании выхода x(n). Если все коэффициенты одинаковы, то алгоритм СС аналогичен формуле (8) вычисления среднего значения, или оценке математического ожидания. Более естественным является выбор коэффициентов b(k) таким образом, чтобы ближайшие к x(n) значения u ( n - к ) учитывались с большим весом. В качестве такой убывающей функции может быть выбрана экспонента.

В работе предлагается использовать известный алгоритм экспоненциального сглаживания x ( n ) = Y " x ( n — 1) + (1 — Y ) ’ u ( n ),                                (14)

который, как и рекуррентная процедура (8), является простейшим БИХ-фильтром первого порядка, или моделью АР(1).

При обработке экспериментальной информации коэффициент y выбирается из диа- пазона

0 <  y < 1,

но, если сравнивать (14) с формулой (5), то численное значение y следует ожидать более близким к единице.

Передаточная функция для уравнения (14) имеет вид

H ₀( z ) =  -----.                                         (16)

1 - y • z

Дискретным моделям экспоненциального сглаживания (14) и (16) соответствует непрерывный аналог в виде простейшего фильтра нижних частот (ФНЧ) с передаточной и весовой функциями:

W о ( 5 ) =

Тф • 5 + 1

t

, х 1        Тх и w (t) =--e ф

T ф

.

Характеристика w(t) изменяется по экспоненциальному закону, отсюда и название ал- горитма. Можно показать, что параметры передаточных функций H0 (z) и W0 (s) связаны выражением

Т

Tф

.

Y = —-—

Т ф + Т

~ ф

Введём в рассмотрение относительные постоянную времени фильтра Т ф = — и часто-

~ 1

ту сопряжения fф = ^^, тогда формулу (17) можно переписать в виде Т ф

Y =

,

~ ф + 1

для которой график зависимости параметра у от f ф для основной полуполосы нормированной частоты f ф е [ 0;0,5 ] приведён на рис. 3.

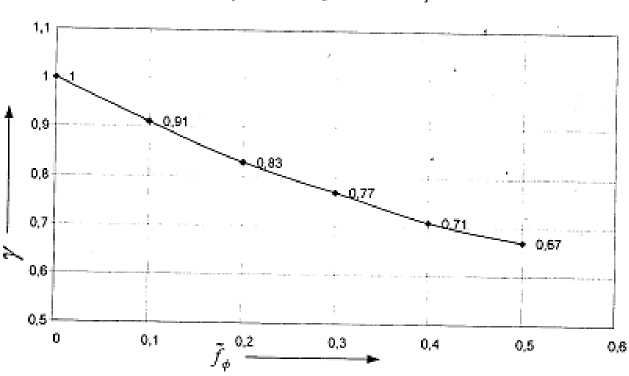
Рис. 3. Зависимость параметра у алгоритма экспоненциального сглаживания

В соответствие с рис. 3 диапазон (15) для коэффициента у изменится и будет определяться неравенством

0,67 <  у < 1.                                    (19)

На этапе предварительных исследований динамических процессов можно выбрать середину основной полуполосы f_ф = 0,25 и соответствующее ему значение параметра экспоненциального сглаживания у = 0,8.

В работе предлагается измеренные (наблюдаемые) дискретные значения E ( n ) процесса естественной освещённости E ( t ) с целью определения тренда (постоянной составляющей) E ₀ ( n ) обрабатывать алгоритмом экспоненциального сглаживания (15), тогда

Eо(n) = y • Eо(n -1) + (1- у) • E(n),(20)

а для вычисления случайной составляющей использовать формулу

E( n) = E (n) - E 0( n) .

Алгоритму цифровой обработки соответствует фильтр нижних частот H ₀( z ) и W ₀ ( s ) , а для выражения (20) можно записать

~                      1 - z ^{- 1}       ~                      Тф • s

H(z) = 1 -H0(z) = Y)-------1 и W(s) = 1 -W3(s) = Г— ---

• 1    - Y •z                             Тф • s +1

то есть уравнению вычисления случайной составляющей E ( n ) соответствует простейший фильтр верхних частот, поэтому алгоритмы (17) и (18) можно использовать для цифровой обработки динамического процесса естественной освещённости.

Вывод

В работе предлагается задачу исследования динамических процессов естественной освещённости E ( t ), E ₀ ( t ) и E ^~( t ) проводить в два этапа. На первом определить моментные характеристики (математическое ожидание, дисперсию, ассиметрию и эксцесс) и эмпирические гистограммы с целью проверки соответствия их теоретическим законам распределения, в первую очередь для тренда E ₀ ( t ) . На втором этапе оценить частотные характеристики и провести спектральный анализ для подтверждения достоверности предлагаемых в работе алгоритмов определения тренда E ₀ ( t ) и случайной составляющей E ( t ) процесса естественной освещённости.