Выбор набора конфигурируемых логических элементов с использованием венгерского метода

Как известно, в программируемых ло-гиических интегральных схемах (ПЛИС, FPGA) широко используются конфигурируемые логические элементы [1]. Основой таких элементов является устройство, называемое в англоязычной литературе LUT (Look Up Table), так как оно реализует задаваемую (загружаемую) таблицу истинности логической функции. Классическое значение количества переменных n =4.

В настоящее время в так называемых адаптивных логических модулях (АЛМ) реализованы LUT с изменяемой разрядностью до 6 переменных, в том числе имеется возможность реализации некоторых логических функций 7 и даже 8 переменных [2]. Функции реализуются в совершенной дизъюнктивной нормальной форме (СДНФ). Существующие принципы реализации систем m логических функций от одних n переменных предполагают использование m LUT.

В статье рассматриваются оценки сложности предложенных конфигурируемых логических элементов, реализующих системы функций в СДНФ и в ДНФ, в том числе ориентированных на самосинхронные схемы (ССС) [3]. Предлагается подход к выбору оптимального набора логических элементов с использованием венгерского метода.

• 1.    Оценка сложности LUT

Сложность LUT [1, 2] в количестве транзисторов без декомпозиции (до n =4) имеет вид выражения

L n = 2 n • 8 + 2 n ^{+ 1} + 6 n ,           (1)

Однако с учетом ограничений Мида–Конвей [4] при декомпозиции сложного дерева по k- LUT, k Є {1,2,3,4}, n > = k, n :

I L n J I

L . k j J

L _k = 2 ^{l n J} • 8 + (2 ^{l k J+ 1} + 6 . k J ) • У 2 ^l n' k ^J +

^.                                                             (2)

+ (2 ^{L n} 41 l^{L k J+ 1} + 6 /. n J - n • . k j ] ) + 6 . n J,

I     LLkJJ    J где 2 k >1 + 6[k J - сложность одного к--дерева [...J – округление в нижнюю строну (floor); таких деревьев (k-LUT) необходимо в первом слое nJ-L^J

2    , затем нужно провести декомпозицию k-LUT этого первого слоя, получаем 2LnJ-LкJ-LkJ. Всего необходимо i к-LUT, где i

I L n J I

^{L L} к ^L n J - L i J - L к J J L n J 11 L n J I ^{у 2           +|} l к j I L l к j J

L 2 J

12 - { У i = 1

определяется из соотношения:

Ч к J

всего

I L n J I

L l к jJ         .

У 2L nj l i J'L kJ и последний LUT на Ln J- i=1

переменных.

Временная задержка в количестве транзисторов определяется выражением

L n J IJ И k ^J

T nk = n + 2

n

И

+ 2 • [

LnJ L W lкj Llкj

].

Для использования в ССС предложен LUT-ST [5]. В этом случае сложность LUT возрастает:

I L n J I L l к j J

L _tST = 2 - {2 ^{L n J} - 8 + (2 ^{L к J+ 1} + 6 L к J ) - X2 n ^{J-LdL к J} +

+ (2

^{+ 6 -} L l n J^- r n i I     L L ^к J.

I L n J I

Л                              L l к j J

- L к J I ) + 6 L n J + 2 - L n J } + 2 - У 2 ^{n J-L} ' ^{J-L к J}

+

n I уjJ 2L. J-LiJ-L* . n JILnJ I i=1                   I l к j I Ll к jJ

^- L i J ’ L ² J

+2 Д n J ] L n J ^{+ 2-}h I ra J

],

где 2 - L n J - сложность дополнительных цепо

чек спейсера, 2 • У 2 ^{L n J L} i ^{J-L к J} i = 1

– сложность ин-

дикаторов k -LUT + индикатор последнего

LUT 2 - [И ^]- I n J .

Lк J   LLк JJ

Выражение (4) не учитывает затраты на фиксацию переходного процесса Г-тригге-рами [3]. Учесть двухвходовые Г-триггеры сложностью 12 транзисторов можно, положив k =2, а n

n

= У 2 L n J - L i J - L к J

LnJ]_ LnJ L к J -Ll к J

Таким образом, получаем сложность Г-триггеров:

LnJ

L к J

Ln J L к J.

}.

Временная задержка LUT-ST в количестве транзисторов (без учета задержки Г-триггеров) увеличивается на задержку индикаторов:

= n + 2

n

И

+ 2 - [

L ⁿ J

+ 2 - у 2 ^{l nк J} +

LnJ L к J

i = 1

Ln J L к J.

Для реализации систем функций в СДНФ предложен DC-LUT [6]. Для ССС с учетом сложности m блоков реализации функций с соответствующей настройкой, получаем сложность DC-LUT-ST:

I L n J I

L l ^k j J

LmdcnisT = 2 - {2LnJ - 8 + (2L к J+1 + 6L к J) - У 2LnJ^JL к J + i=1

L n J ^- I kJ ^|- L ^к J ^{+ 1} + (2    ^{LL к JJ}

¹ L n J¹

L l к j J

2 _- У 2 L n J - L i J - L к J i = 1

^{+ 6 -}fi ⁿ J ^- у L       L L ^к J.

+ 2 - [

L к J

^- L ^к J I ) ^{+ 6} L ⁿ J ^{+ 2 -} L ⁿ J ^{} +}

Ln J Lк J.

L n J

+ У 2^J + 6 m (2 ⁿ + 2)], j = 1

(8) где 6 m (2 ⁿ + 2) - сложности m блоков реализации функций.

Для реализации систем функций в ДНФ предложен ДНФ-LUT [7]. При использовании ДНФ-LUT получаем сложность в количестве транзисторов:

L dnf

= L k J - (20_n J + 2 - ° ) + 6 - L m J ( L k J + 2) + 6 L n J , ⁽⁹⁾

где L k J - (20 L n J + 2 - n) учитывает сложность реализации k настраиваемых конъюнкций;

_{2 -} n

– учитывает сложность инверторов в

блоке конъюнкций, в том числе для удовлетворения ограничения Мида–Конвей [4] в блоках конъюнкций; 6 - [ m J ( [ k J + 2) - сложность m блоков функций от k конъюнкций (реализация монтажного И); 6 [ n J - сложность инверторов по n переменным (два на неинверсный вход, один на инверсный).

Тогда сложность ДНФ-LUT-ST без Г-триггеров определяется выражением:

L dnf-ST = 2 - { [ k J - (20 [ n J + 2 -

2 ) + 6 ^-[ mJ [ k J + ²⁾ + 4 [ n J} ,

(10) где 4 [ n J учитывает инверторы по n пара-фазным переменным (один на каждый вход, 2 [ n J и цепочку спейсера - один транзистор на каждый парафазный вход, всего 2 [ n J .

Сравнение выражений сложности предлагаемых технических решений изображено на рис. 1.

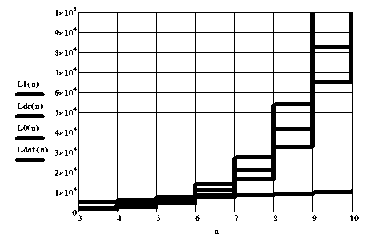
Рис. 1. Сравнение L0(n), L1(n), Ldc(n), Ldnf(n) при m=8; k=3; r=20

Таким образом, ДНФ-LUT-ST выигрывает по сложности реализации при большом количестве переменных системы логических функций. При среднем количестве переменных целесообразно использование DC-LUT-ST.

выражениям сложности (10, 9, 8, 4, 3, 2) и/или времени (3, 7) для заданных параметров системы функций. Для учета возможности покрытия одним типом устройства нескольких систем возможно использовать повторение строки матрицы.

Предлагаемый алгоритм выбора конфигурируемых логических элементов, реализующих системы функций с использованием венгерского метода, изображен на рис. 2.

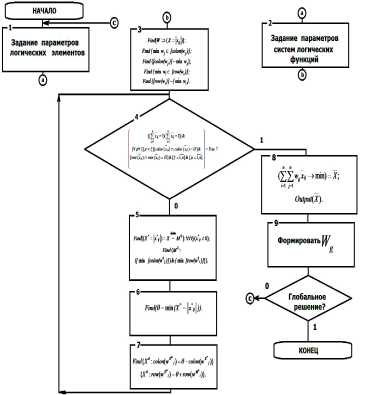
Рис. 2. Алгоритм выбора конфигурируемых логических элементов, реализующих системы функций с использованием венгерского метода

В качестве вариантов реализации систем логических функций можно рассмотреть:

• 1)    LUT по числу требуемых функций в системе;

• 2)    DC LUT на заданное максимальное число функций;

• 3)    ДНФ-LUT на заданное максимальное число конъюнкций и функций;

• 4)    варианты комбинирования 1–3. Получим матрицу назначений W следующим образом: каждой строке соответствует вектор, отображающий количество каждой из формул, принимающих участие в расчете.

Так, вектору для первой строки (10,0,0,0) соответствует сумма из десяти формул 1, вектору для второй строки (0,10,0,0) – сумма десяти вторых формул, вектору для третьей строки (0,0,0,10) – сумма десяти третьих формул, вектору для четвертой строки (3,3,4,0) – сумма трех первых, трех вторых и четырех третьих формул. При этом каждому столбцу матрицы назначений W соответствует аргументы m, k и n.

Пример результатов расчета представлен на рис. 3.

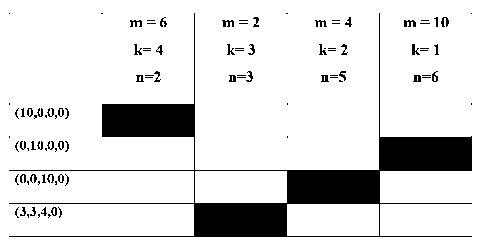
Рис. 3. Пример результатов расчета

Расчеты показывают, что предлагаемый DC LUT FPGA предпочтительней по аппаратным затратам, чем известный LUT уже при количестве функций m =8 для числа переменных n =4. Предлагаемый логический элемент ПЛИС – ДНФ FPGA на основе ДНФ по сравнению с ЛЕ-СДНФ выигрывает при переходе к восьмиразрядным функциям (для n=k=m ).

При этом существующий ЛЕ не может реализовать даже 32 разрядные функции, а предлагаемый имеет приемлемые затраты даже для 64 разрядных функций. Причем быстродействие предлагаемого варианта так же, как и известного, определяемого в основном длиной цепочки передающих транзисторов – n , определяется цепочкой транзисторов в блоках программируемых конъюнкций – это тоже n, а цепочки в блоках программируемых функций содержат всего один транзистор.

Полагаем, в дальнейшем целесообразно использовать средние характеристики затрат w на реализацию различных систем логических функций, которые были получены путем анализа типовых проектов, загружаемых в ПЛИС.

• 1.    Строгонов А., Цыбин С. Программируемая коммутация ПЛИС: взгляд изнутри. URL: http://www.kite.ru/articles/plis/2010_11_56.php (дата обращения: 13.03.2017).

• 2.    Золотуха Р., Комолов Д. Stratix III – новое семейство FPGA фирмы Altera. URL: http://kit-e.ru/assets/files/pdf/2006_12_30.pdf (дата обращения: 14.03.2017).

• 3.    Степченков Ю.А., Денисов А.Н., Дьяченко Ю.Г.и др. Библиотека элементов для проектирования самосинхронных полузаказных микросхем серий 5503/5507 и 5508/5509. М.: ИПИ РАН, 2014. С. 150–151.

• 4.    Ульман Дж. Д. Вычислительные аспекты СБИС / пер. с англ. А.В. Неймана; под ред. П.П. Пархоменко. М.: Радио и связь, 1990. 480 с.

• 5.    Тюрин С.Ф., Каменских А.Н., Плотникова А.Ю. Программируемое логическое устройство. Патент РФ № 2601145. Опубл. БИ № 30 27.10.2016.

• 6.    Тюрин С.Ф., Вихорев Р.В. Программируемое логическое устройство. Патент РФ № 2573732. Опубл. БИ № 3 27.01.2016.

• 7.    Тюрин С.Ф. Программируемое логическое устройство. Патент РФ № 2544750. Опубл. БИ № 8 20.03.2015.

• 8.    Harold W. Kuhn. "The Hungarian Method for the assignment problem", Naval Research Logistics Quarterly, 2:   83–97,   1955;

• 9.    Hungarian algorithm. URL:

(дата обращения: 02.02.2017).