Выбор параметров алгоритма распознавания изображений на основе коллектива решающих правил и принципа максимума апостериорной вероятности

Основной проблемой в области автоматического распознавания изображений (АРИ) [1,2] является недостаточная устойчивость существующих моделей изображений к искажениям (noise) [3] и, как следствие, недостаточная точность традиционных методов классификации [2] в условиях априорной неопределённости (неизвестная заранее освещённость, размер, ракурс, положение распознаваемого объекта на изображении и пр.). Известно [2], что большинство современных математических моделей изображений зависит от ряда параметров: диапазон изменения используемого признака (например, градация яркости), размер сетки, на которую разбивается входной объект с целью учёта вариативности освещения [4], и многие другие. При этом качество АРИ для фиксированной модели может значительно варьироваться в зависимости от различных значений её параметров. Зачастую исследователи ещё на этапе анализа предметной области фиксируют все параметры, полагаясь исключительно на свой опыт и интуицию.

Очевидно, такое решение не всегда можно считать достаточно разумным. Поэтому в данной работе рассматривается логика рассуждений совсем другого рода. Исследователю предлагается зафиксировать лишь некоторое конечное множество потенциально оптимальных параметров. При этом выбор конкретного набора происходит автоматически на основе синтеза коллективов решающих правил (КРП, комитетов классификаторов, алгоритмических композиций) [5, 6]. В работе проводится сравнение КРП, полученных с помощью традиционного усреднения индивидуальных решающих правил [7, 8], с КРП, построенными на основе принципа максимума апостериорной вероятности [9, 10]. Полученные результаты и сделанные по ним выводы рассчитаны на широкий круг специалистов в области распознавания изображений.

Алгоритм SIFT в задаче автоматического распознавания изображений

Пусть задано множество из L > 1 полутоновых изображений Xl = |xUlv’Ц , l = 1, L, и = 1, U , v = 1, V . Здесь U – высота изображения, V – его ширина; x(l,) е{1,2, ^, xm„„} - интенсивность точки изобра-uv               max жения с координатами (u,v); xmax – максимальное значение интенсивности, l – номер эталона в БД. Задача распознавания изображений состоит в том, чтобы отнести вновь поступающее (на вход) изображение X =||xuv|| к одному из классов, заданных эталонами Xl. Каждый класс характеризуется тем, что принадлежащие ему объекты обладают некоторой общностью или сходством в характеристиках. То общее, что объединяет объекты в класс, и называют образом [11].

Для решения задачи АРИ воспользуемся популярным сейчас методом SIFT (Scale-Invariant Feature Transform) [4]. Вначале выполним предварительную нормировку [12] освещения изображений из базы (например, используя гамма-коррекцию с последующей медианной фильтрацией [13]). В качестве основного признака [14, 15] выбирается направление градиента яркости пикселя, вычисленное по формуле Робертса (применяющегося, например, в наиболее популярном детекторе краёв Кэнни [13])

e ulv =п+ arctg

( l )                   ( l )

' и +1, v +1     x u , v

( l )

x u +1, v

( l ) u ,

Направление градиента 0 Ul ) _v полностью инвариантно к интенсивности освещения (определяющего только модуль градиента).

Далее разобьём каждое изображение квадратной сеткой из S х T ячеек (по S строк и T столбцов, в оригинале [4] S = T = 4). Для каждой ячейки вычис-

лим взвешенную гистограмму направления градиента яркости. В качестве веса используется оценка модуля градиента

( l )                ( l )                ( l ) ²            ( l )             ( l )        ²

m u , v     ( X ^Xu +1, v +1    ^Xu , v ) + X ^Xu +1, v   ^Xu , v +1 ) •

Для вычисления гистограммы Hl(s, t) направле- ния градиента в ячейке (5, t), 5 = 1, S, t = 1, T разобьём всю область определения [-3п]4; 5л/4] на N отрезков одинакового размера 2п / N (в оригинале [4] N = 8). Тогда элемент гистограммы может быть оценён как hi(l) (5,t)

h il ) X 5 , t ) = / ^X , ) , i = 1, N •                       (2)

Z h^ l ) X 5 , t )

i =1

Здесь

U • 5 / S

h⁽ l ) X 5 , t ) = Z

V • t / T

Z

u = U •( 5 -1)/ S +1 v = V •( t -1)/ T +1

_m ( l )

^uv x

m ⁽ l ) X r , c )

x H I 0 uv

2( i - 1) - N N

- h ^0 uv’

21 - N )) --n ,

N ))

m

а H ( x ) =

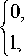
x <  0, x >  0

– функция Хэвисайда и

^{X 5} , t )

max

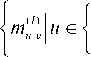
U • ( 5 - 1) S

⁺ 1,

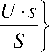
v e

Г V • ( t - 1) ₊ 1

[ t ^:

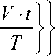
Решение в алгоритме SIFT принимается по критерию минимума некоторой меры близости между гистограммами направления градиента входного изображения и эталонов из БД. Наиболее распространено применение в качестве рассогласования l 2 -метрики (Евклида)

ции от ряда параметров модели. В частности, для SIFT важными являются следующие параметры – размер сетки для разбиения изображения ( S, T ), мера близости гистограмм направления градиента яркости, число интервалов в диапазоне изменения направления градиента яркости пикселя ( N ), размер окна медианного фильтра, необходимость в выполнении опциональных этапов алгоритма. Очевидно, эти параметры могут принимать множество значений, при этом точность распознавания определяется не только свойствами БД { X l }, но и характеристиками входного объекта X [16]. Таким образом, даже для одного и того же множества эталонов качество классификации для фиксированного набора параметров может существенно варьироваться в зависимости от распознаваемого изображения. Похоже, невозможно заранее подобрать универсальные значения этих параметров так, чтобы обеспечить оптимальную классификацию для различных задач АРИ.

В условиях полной априорной неопределённости одним из наиболее естественных способов преодоления проблемы выбора наилучших параметров может служить построение КРП [5, 6], в котором каждое решающее правило представляет собой реализацию алгоритма SIFT для конкретного набора параметров. Обзор и анализ публикаций в области обработки данных показывает, что синтез КРП является одним из наиболее эффективных подходов к увеличению точности и устойчивости классификации [17]. В КРП для принятия решения о классификации изображения используется не один, а несколько критериев, каждый из которых самостоятельно присваивает метку класса, после чего на основе некоторого принципа [5] формируется общий результат классификации.

Таким образом, задача состоит в следующем. Вначале исследователем выбирается несколько альтернативных наборов значений параметров, между которыми и требуется осуществить выбор. Можно считать, что эти наборы задают семейства рассогласований p = {p k ( x1, x2)}, k = i:K,                       (4)

где K – количество вариантов (альтернативных наборов параметров алгоритма АРИ). Каждое рассогласование задаёт критерий АРИ, согласно которому решение принимается в пользу класса, соответствующего эталону X * , где l ( k )

I * ^{( k} ) = argmin p k ⁽ X , X l ).                         ⁽⁵⁾

l e { 1... L }

В результате процедуры АРИ объекта X для каждого рассогласования (3) будет получен вектор

p ; = [ p k ( X , X 1 ), p k ( X , X 2 ), ™ p k ( X , X_L ) ] •

Тогда требуется по набору векторов p _k , k = 1, K («мнений экспертов») определить тот p ^ из них, который наиболее подходит для АРИ объекта X .

Наиболее простые способы построения КРП [1, 7], такие как голосование членов комитета и усреднение выходов классификаторов ( р k ( X , X l )) по ансамблю к = 1, K , не подходят для поставленной задачи выбора параметров алгоритма АРИ. Во-первых, они предполагают, что члены комитета в среднем одинаково эффективны (в смысле точности классификации). Однако в реальности для каждого распознаваемого изображения вполне возможна ситуация, когда один критерий подходит лучше всех остальных. И, во-вторых, такое построение комитетов предполагает, что количество членов комитета будет достаточно большим. А на практике уже использование более трёх классификаторов приводит к невозможности реализации системы АРИ в режиме реального времени (например, при распознавании объектов на видеоизображении).

Очевидное решение состоит здесь в использовании более сложных алгоритмов построения КРП, основанных на алгебраическом подходе [5, 18]. Б о льшая часть таких алгоритмов (такие как комитет взвешенного большинства [18], бэггинг и бустинг [17]) требуют достаточно представительной обучающей выборки. К сожалению, во многих задачах АРИ имеющаяся БД содержит недостаточное число эталонов для каждого класса (в худшем случае, один эталон на класс). В настоящей работе предлагается воспользоваться известными статистическими способами синтеза КРП [1], когда тем или иным способом для каждого члена комитета определяются вероятности принадлежности входного объекта к классам из БД. Как следствие, встаёт задача присвоения таких вероятностей на основе только данных р _к , к = 1, K о расстоянии от входного изображения до всех эталонов из БД для произвольных мер близости. Далее мы проведём строгий вывод выражения для апостериорной вероятности принадлежности объекта к классу из БД для информационного рассогласования Кульбака–Лейблера [19].

Принцип минимума информационного рассогласования в задаче распознавания изображений

Для применения статистического подхода [1, 15] предполагаем, что 9 ( V является реализацией случайной величины - направления градиента 0 l изображения-эталона X _l .

Задача сводится в таком случае к проверке L гипотез о распределении [20] H l , 1 = 1, L , сигнала изображения на входе H :

Wl : H = Hl .                               (6)

Оптимальное решение тогда даёт классический байесовский подход [1, 10] – критерий максимума апостериорной вероятности PW\X} того, что справедлива гипотеза Wl при появлении на входе объекта X, то есть изображение X принадлежит классу, заданному эталоном Xl . Эта вероятность вычисляется по формуле Байеса

. . ,    P { XW } ■ P { W }

P { Wl | X } = _L l .                  (7)

tp {XW }■ p {W} i=1

Здесь P { W l } - априорная вероятность появления 1 -го класса, P { XW } - правдоподобие, т.е. условная вероятность принадлежности объекта X классу . В большинстве задач распознавания изображений предполагается, что появление каждого класса равновероятно (полная априорная неопределённость). В этом случае решение (3) принимает наиболее простой вид

P { XW } ^ max .

Учитывая наше предположение о том, что гистограмма H ₉ . _; является оценкой распределения направления градиента точки изображения 0 для класса , условная вероятность

Г 8( i — 1) — 3 N       , . 8 i — 3 N     1 . _ч

P<-------------- п < 0 ( 5 ; t ) <---------п W, ^ = h^{( 1 )} ( 5 , t ).

[     4 N                   4 N ¹J i

Далее, делая «наивное» предположение о независимости [21] направлений градиентов яркости в соседних точках изображения, нетрудно показать [20,21], что условная вероятность P { XW } может быть записана как

P { XW } =

Г TVStn _   ,1

= exp wfSEE( hi (5, t) ln hi (5, t ))rx

I ST s=1 t=1 i=1

Г UV1

^X exP I ST P KL ( X ^X1 ) [ •

Здесь

STN

PKL(X\Xe) = XZt h.(».t)Int;^(10)

s =1 t = 1 i =1 ^                 h i ( ^{5 ,} t ) ^

– информационное рассогласование Кульбака– Лейблера [19].

В результате получаем, что оптимальное в байесовском смысле решение задачи (то есть эквивалентное (6)) проверки гипотез о распределении дискретной случайной величины (4) даёт принцип минимума информационного рассогласования Кульбака–Лейблера. Поэтому критерий максимума апостериорной вероятности (7) эквивалентен правилу ближайшего соседа [1]

l* = argmin р K _L ( ^X| X i ) .                          ⁽¹¹⁾

1 =1, L

Таким образом, оптимальное в байесовском смысле решение задачи классификации изображений принимается по критерию минимума решающей статистики (10).

Принцип максимума апостериорной вероятности

В настоящей работе для решения задачи выбора параметров алгоритма АРИ (4), (5) предлагается определять наилучший критерий р_ц на основе классического принципа максимума апостериорной вероятности [1]

ц — argmax P { W ll X }| .

k е { 1,-.., K }      ^{1 lk}

Исходя из формулы условной вероятности (9), выражение для апостериорной вероятности P { W, | X } будет иметь предельно простой вид

P №}

J UV / _v \1 exp 1— ST^KL ( X I X/ ) £ exp J- UV -p^ U\X. Л

KL i i — 1          k                                         J

В результате имеем следующее решение задачи выбора параметров (4), (5), основанное на принципе максимума апостериорной вероятности

exp

ц — arg max k e { 1,-.., K }

J UV

Л--" О

I ST KKL

I ^Sk^Tk

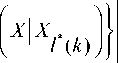
Как известно [4], качество АРИ для метода SIFT определяется прежде всего размером сетки ( S и T ) и применяемой мерой близости для сопоставления гистограмм направления градиента (2). Поэтому в настоящем эксперименте производится выбор значений именно этих параметров.

Сетка размером ( S = T = 4) из оригинального алгоритма SIFT [4] оказалась недостаточной для сложной задачи распознавания лиц и показала низкую точность классификации для всех наших экспериментов. Поэтому далее, кроме оригинальных значений параметров, рассматриваются сетки б о льшего размера: S = T = 10, S = T = 15 и S = T = 20.

В качестве мер близости в методе ближайшего соседа (11) воспользуемся традиционной метрикой Евклида (3) и теоретически оптимальным рассогласованием Кульбака–Лейблера (10). Кроме них, применяется симметричное информационное расхождение Кульбака [19], которое также рекомендуется использовать для решения задач статистической классификации

^ exp I-- UV- p_KT f x l x jl ^f П S k T k KKL ( I I )

. (14)

k

J ( X : X / ) —

Здесь S_k , T_k – размер сетки для k -го набора параметров.

Заметим, что в выражении (14) используются только компоненты векторов p _k , k — 1, K . Поэтому окончательно в настоящей работе предлагается следующее решение задачи выбора (4), (5)

a                    h ( ⁵ , t )          ( ¹⁶ )

^— EH( h i ^{( 5} , t ^)- h ⁽) ^{( 5} , t ) ) '",

5 —1 t —1 i —1                                           h i ( ⁵ , t )

В эксперименте проводилось сравнение точности АРИ для индивидуальных решающих правил (с фиксированным набором параметров) с точностью КРП, построенных на основе предлагаемого критерия (15), а также с КРП, полученных по алгоритму агрегирования [26]

ц — arg max k e { 1,-.., K }

J UV \ expX,X,-„.

_{S T} k         l ( k )

kk

J UV f exP FVF‘P k ( X, Xl )

l —1        I ^Sk^Tk

Разумеется, это решение будет оптимально (эквивалентно принципу максимума апостериорной вероятности (12)) только в том случае, если семейство (4) состоит только из информационных рассогласований Кульбака–Лейблера. Тем не менее, далее в экспериментальном исследовании мы покажем, что критерий (15) позволяет определить оптимальные наборы параметров для более широкого круга мер близости.

Программа экспериментальных исследований

Для проведения экспериментального исследования эффективности предложенного критерия (15) выбора оптимальных параметров алгоритма АРИ рассмотрим задачу классификации людей по фотографиям лиц [22], являющейся, как известно [23], одной из наиболее сложной в области распознавания образов. В качестве их предварительной обра- ц — argmin f/ (n; k),                        (17)

n e { 1,-, ^K } k —1

l f ,      P { W l\ X } '

где / ( n ; k ) — f P { W|X } - In ⁿ ,

7:1    1 1 j|n    p {wl\X}

V                              ^k 7

a P { W l| X }| и P { W\X }| k - оценки апостериорной вероятности (13) для наборов параметров с индексами n и k соответственно.

Результаты экспериментальных исследований

Для БД Yale (вариативный параметр – неравномерная освещённость объекта) в БД эталонов помещались 15 изображений (по одной фотографии каждого человека), а тестирование качества распознавания проводилось на остальных снимках этих же людей (181 фотография). Тем самым достигались наиболее жёсткие условия для последующего распознавания (one sample per person [27]).

Для БД AT&T, в которой вариативным параметром является ракурс объекта на изображении, в качестве множества эталонов использовались L = 110

изображений 40 различных людей, а тестирование качества АРИ проводилось на других снимках (291 фотография).

Все результаты – оценки вероятности ошибки АРИ – для трёх БД и индивидуальных решающих правил сведены в табл. 1.

		Yale	AT&T
Метрика Евклида (3)	S=T= 4	13,3%	7,5%
	S=T= 10	7,3%	2,5%
	S=T= 15	7,3%	4,5%
	S=T= 20	3%	5,75%
Информационное рассогласование (10)	S=T= 4	11,5%	5,75%
	S=T= 10	6,6%	3%
	S=T= 15	6,1%	4%
	S=T= 20	2,4%	6%
Информационное расхождение (16)	S=T= 4	11,5%	5,5%
	S=T= 10	6,7%	2,7%
	S=T= 15	6,7%	4%
	S=T= 20	1,8%	6%

Далее в табл. 2 приведены вероятности ошибки для КРП, построенных при нескольких возможных комбинациях параметров из табл. 1 для БД Yale. Проводится сравнение синтезированного критерия (15) с традиционным агрегированием (17). Кроме того, в столбце «Лучшее РП» (решающее правило) показана наименьшая вероятность ошибки для индивидуальных критериев из комитета.

Проиллюстрируем действие предлагаемого подхода к построению КРП на примере изображений из БД Yale (рис. 1).

а)

Рис. 1. Распознаваемый объект (а), ближайший в смысле рассогласования Кульбака–Лейблера (10) эталон (S = T = 20) (б); ближайший в смысле рассогласования Кульбака–Лейблера (10) эталон (S = T = 10) (в)

Распознаваемое изображение (рис. 1 а ) подавалось на вход критерия (10) для размеров сетки 4, 10, 15 и 20 (вторая строка табл. 2). Несмотря на то, что в целом для этой базы эталонов точность критерия с большой сеткой ( S = T = 20) в среднем существенно лучше остальных, в этом случае для этого набора параметров было получено неверное решение АРИ (рис. 1 б ). И только для сетки ( S = T = 10) решение в пользу эталона (рис. 1 в ) принято верно. Действительно, для S = T = 10 в данном случае апостериорная вероятность (13) максимальна. В то же время для решающего правила с S = T = 20 рассогласование между входным объектом (рис. 1 а ) и эталонами (рис. 1 б и рис. 1 в ) практически совпадает: 0,266 и 0,269 соответственно.

Таблица 2. Вероятность ошибки АРИ для КРП (15), (17) и БД Yale

		Лучшее РП	(17)	(15)
Мера близости	Размер сетки	3%	4,8%	2,4%
(3)	S=T= 4
(3)	S=T= 10
(3)	S=T= 15
(3)	S=T= 20
Мера близости	Размер сетки	2,4%	6,1%	2,4%
(10)	S=T= 4
(10)	S=T= 1 0
(10)	S=T= 15
(10)	S=T= 20
Мера близости	Размер сетки	1,8%	10,3%	1,8%
(16)	S=T= 4
(16)	S=T= 10
(16)	S=T= 15
(16)	S=T= 20
Мера близости	Размер сетки	3%	5,5%	3,6%
(3)	S=T= 10
(3)	S=T=20
Мера близости	Размер сетки	2,4%	3%	2,4%
(10)	S=T= 10
(10)	S=T= 20
Мера близости	Размер сетки	1,8%	3,6%	2,4%
(16)	S=T= 10
(16)	S=T= 20
Мера близости	Размер сетки	6,6%	7,3%	6,6%
(3)	S=T= 10
(10)	S=T= 10
(16)	S=T= 10
Мера близости	Размер сетки	1,8%	3%	1,8%
(3)	S=T= 20
(10)	S=T= 20
(16)	S=T= 20

Поэтому и апостериорная вероятность принадлежности объекта (рис. 1 а ) к эталону (рис. 1 б ) невелика. В то же время для сетки S = T = 20 рассогласования между распознаваемым объектом и эталонами (рис. 1 б, в ) заметно различаются: 0,254 и 0,212 соответственно.

По результатам проведённых экспериментов (табл. 1 - 3) можно сделать следующие выводы. Во-первых, точность классификации действительно во многом определяется выбранными параметрами алгоритма АРИ.

		Лучшее РП	(17)	(15)
Мера близости	Размер сетки	2,5%	4,2%	2,7%
(3)	S=T= 4
(3)	S=T= 10
(3)	S=T= 15
(3)	S=T= 20
Мера близости	Размер сетки	3%	4,5%	2,5%
(10)	S=T= 4
(10)	S=T= 10
(10)	S=T= 15
(10)	S=T= 20
Мера близости	Размер сетки	2,7%	6%	2,5%
(16)	S=T= 4
(16)	S=T= 10
(16)	S=T= 15
(16)	S=T= 20
Мера близости	Размер сетки	2,5%	2,7%	2,7%
(3)	S=T= 10
(10)	S=T= 10
(16)	S=T= 10
Мера близости	Размер сетки	5,75%	5,5%	5,7%
(3)	S=T= 20
(10)	S=T= 20
(16)	S=T= 20

При этом набор параметров метода SIFT, предложенный в оригинальной работе [4] (в частности, сопоставление гистограмм в метрике Евклида и небольшая сетка S = T = 4), оказался недостаточно эффективным в столь сложной задаче распознавания образов, как распознавание лиц. Во-вторых, традиционный способ построения КРП за счёт усреднения результатов индивидуальных решающих правил [1, 7] недостаточно эффективен в задаче выбора оптимальных параметров (по сравнению с наилучшими индивидуальными критериями). И, в-третьих, синтезированный на основе принципа максимума апостериорной вероятности критерий (15) показал высокую эффективность, причём не только для теоретически оптимального рассогласования Кульбака–Лейблера (10), но и для симметричного информационного расхождения (16) и традиционной метрики Евклида (3).

Заключение

Известно [1, 5], что один из наиболее эффективных подходов к увеличению точности и устойчивости классификации основан на синтезе КРП. В них для принятия решения о классификации изображения используется не один, а несколько критериев, каждый из которых самостоятельно присваивает метку класса, после чего формируется общий результат классификации, например, с помощью простого голосования членов комитета. На большинстве выборок неоднородные КРП, сформированные в известных публикациях, улучшали точность классификации на 3+10% [26].

К сожалению, как было отмечено выше, большинство традиционных способов построения КРП [5, 17] не могут эффективно применяться в задаче выбора оптимальных параметров алгоритма АРИ. Действительно, они либо предъявляют достаточно жёсткие требования к объёму обучающей выборки, либо накладывают ограничение на равноценность всех параметров-кандидатов. Наиболее подходящим здесь представляется использование статистического подхода [1] и, в частности, классического принципа максимума апостериорной вероятности.

В настоящей работе показано, что критерий (15) обеспечивает максимум апостериорной вероятности принадлежности входного объекта к классу из БД, если во всех индивидуальных правилах (5) используется информационное рассогласование Кульбака– Лейблера. Однако наиболее важным следует признать то, что критерий (15) позволяет получить высокую точность АРИ и для других, более популярных и точных, расстояниях – традиционная метрика Евклида (3) и симметричное информационное расхождение (16). Действительно, несмотря на то, что рассогласование Кульбака–Лейблера (10) является статистически оптимальным (в смысле эквивалентности наивному байесовскому правилу), на практике точность АРИ для (10) существенно ниже аналогичного показателя для (16). Это может быть объяснено тем, что само предположение о статистической независимости признаков, лежащее в основе классификатора Байеса, является слишком «наивным» в задаче АРИ. И тем ценнее тот факт, что синтезированный критерий (15) показывает высокие результаты и в реальных практических задачах распознавания лиц.