Выбор параметров цифровых фильтров при спектрофотометрических исследованиях

В различных областях знаний при исследовании изменяющихся процессов, по отклику, получаемому с помощью физического прибора, анализируемый сигнал условно можно разделить на две компоненты: «полезный» сигнал и сигнал «помех». Так, например, в спектроскопии выделяют линии поглощения и сигнал, обусловленный шумом различной природы [1–4]. А в инженерных исследованиях при изучении влияния размерных факторов, связанных с неровностью поверхности системы, на адгезию, смачиваемость, трение и т. п., рельеф поверхности разделяют на шероховатость, волнистость и отклонение формы от базовой линии. Отмеченные факторы в конкретных исследованиях можно считать «полезным» сигналом или сигналом «помех» и при этом возникает проблема подавления «помех». Данная проблема решается с помощью разнообразных физических и цифровых фильтров [5].

В процессе решения задач качественного и количественного спектрофотометрического анализа спектрофотометрическую информацию можно разделить на «полезный» сигнал и «помехи».

Перед обработкой спектров поглощения наноструктур (назовем эти спектры «полезным» сигналом), например, в ИК-спектрах конденсированных сред, появляется необходимость предварительной фильтрации исходного спектра от «помех». Эти «помехи» могут быть вызваны факторами различной природы. Например, наличием нескомпенсированных спектров поглощения атмосферы, влиянием спектров адсорбированных на поверхности образца молекул, наличием интерференционных помех в тонких или многослойных объектах. Искажение формы и параметров полос поглощения может также существенно повлиять на погрешности последующей обработки спектров, например, для расчетов оптических характеристик сред по формулам Френеля, Кра-мерса–Кронига, классического дисперсионного анализа. Сложность фильтрации «полезного» сигнала от «помехи» заключается в том, что они могут обладать схожими контурами полос поглощения. Наиболее часто для описания контуров полос используют контуры лоренцевской и гауссовской формы. Для спектральной линии, описываемой данными контурами, основными являются следующие параметры: положение полосы поглощения, интенсивность и полуширина (FWHM). Особый интерес в связи с поставленными задачами качественного и количественного спектрофометрического анализа представляет влияние на параметры спектра вида фильтра и его характеристик. Существует множество способов фильтрации спектров [4]. В рамках данной работы авторы сравнили влияния наиболее часто используемых при спектрофотометрических исследованиях медианного фильтра и оконных фильтров Савицкого–Голая [4–8] нулевого–первого, второго–третьего, четвертого–пятого порядков [4, 9] на параметры полос поглощения, описываемых контурами лоренцевской и гауссовской формы. Задача решалась методами математического моделирования.

Моделирование контура одиночной полосы поглощения и конструирование фильтров

Полоса поглощения, описываемая контуром Гаусса, моделировалась с помощью выражения:

T ( у ) = 1 - h₀ exp

- 4 • In 2 •

( у - У о ) 2

FWHM ₀

контур полосы поглощения лоренцевской формы аппроксимировался формулой:

T ( у ) = 1 - h o

FWHM ₀ ²

FWHM 2 + 4( у - у ₀)²

где h ₀ - интенсивность максимума (отн. ед.), у - волновое число (см^-1), у о - волновое число, соответствующее максимуму поглощения (см^–1), FWHM 0 – полуширина полосы поглощения (см^–1).

Модели контуров полос поглощения (1) и (2) использовались в качестве входных данных для оконных фильтров. Эти модели дискретизировались с частотой дискретизации dу, при этом соблюдалось соотношение: dу «FWHM0. Результатом дискретизации была функция Ti, где i е (0; N).

Результат фильтрации спектра для фильтра Савицкого–Голая вычислялся как:

M

Yt= £ CT+k , k=-M где T – входная функция поглощения, Y – фильтрованная функция, C – весовые коэффициенты оконного фильтра, M – параметр фильтра, характеризующий количество точек, используемых для фильтрации, количество которых считалось как 2M + 1 .

Для фильтра нулевого–первого порядка коэффициенты оконного фильтра Савицкого–Голая (SG0) рассчитывались по формулам [4, 6, 8]:

Ck = 1(2 M +1), для фильтра второго–третьего порядка (SG2):

C = 3(3 M 2 + 3 M -1 - 5 k 2) k = (2M + 3)(2M +1)(2M -1), для четвертого–пятого порядка (SG4):

Физика

C _ 15 63k2 - 35(2M2 + 2M - 3)k2 +15M4 + 30M3 - 35M2 -50M +12 k = 4         (2M + 5)(2M + 3)(2M +1)(2M -1)(2M - 3)         , медианный фильтр (Median) реализовывался в соответствии с [9]:

Y i = med(T_k ), k e ( i - M ; i + M ), ширину окон фильтров рассчитывали как:

WW = d v • 2 M .

Обсуждение результатов моделирования

Основные результаты моделирования влияния фильтрации на параметры модельной полосы поглощения представлены на рис. 1–4. Согласно рис. 1 все оконные фильтры, рассмотренные в данном исследовании, не изменяли положения максимума полосы поглощения v ₀, что является важным результатом, позволяющим использовать данный параметр для последующей идентификации спектра.

Для исследования влияния ширины окна фильтра на изменение интенсивности и формы контура был проведен численный эксперимент. На рис. 1 приведены основные результаты по изучению искажения интенсивности гауссовского контура поглощения в зависимости от относительной ширины окна WW / FWHM = 4,75 . Сплошной линией изображен контур полосы поглощения до фильтрации, точечной линией – контур после фильтрации. Из полученных данных следует, что медианный фильтр практически не искажает контур полосы поглощения, однако происходит обрезание интенсивности контура. Фильтр Савицкого–Голая SG0 – значительно уширяет полосу поглощения, существенно уменьшая ее интенсивность; фильтр SG2 – при данном соотношении WW / FWHM несколько искажает форму полосы поглощения, появляются дополнительные боковые полосы, меньше искажается полуширина максимума и его высота; фильтр SG4 в данном случае вносит наименьшие искажения, однако при увеличении ширины окна появляются иска-

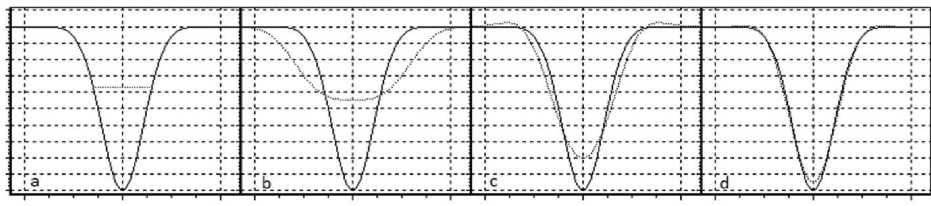
Рис. 1. Характер искажения полосы поглощения гауссовской формы различными фильтрами: a) Мedian; b) SG0; c) SG2; d) SG4

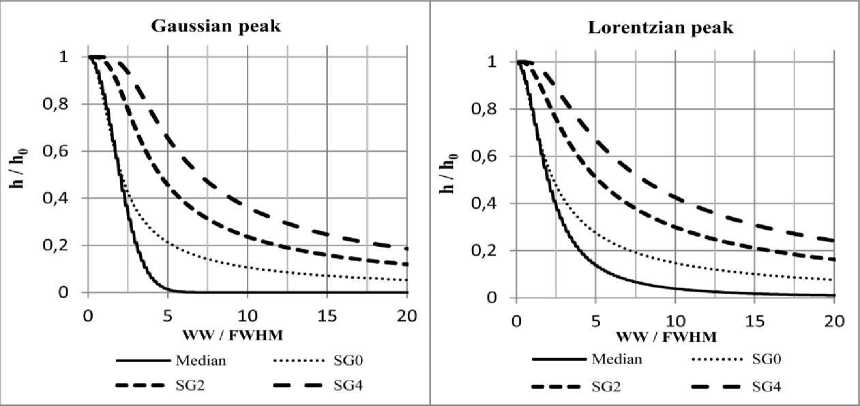
Рис. 2. Изменение относительной высоты максимума в зависимости от относительной ширины окна фильтров жения, аналогичные фильтру SG2. Общий характер искажения формы лоренцевской полосы поглощения аналогичен рассмотренным результатам для полосы поглощения гауссовской формы.

Для обобщения результатов исследования они представлены в безразмерных величинах. На рис. 2 приведена зависимость отношения интенсивности полосы поглощения после фильтрации h к начальной интенсивности полосы h 0 в зависимости от относительной ширины окна (отношения ширины окна WW к параметру полосы поглощения FWHM ). Полученные результаты позволяют сделать вывод, что искажение интенсивности полосы гауссовской формы при малых значениях параметра WW / FWHM меньше, чем для полосы лоренцевской формы. Однако при увеличении этого параметра (абсцисса на графике) уменьшение значения интенсивности полосы лоренцевской формы становится меньше, чем для гауссовской формы. Контур гауссовской полосы поглощения при WW / FWHM >  5 и лоренцевской полосы при WW / FWHM >  20 практически полностью подавляется медианным фильтром.

Для более детального изучения искажений контура полос поглощения были построены зависимости, изображенные на рис. 3 и рис. 4. Из полученных результатов следует, что для контура гауссовской формы и искажении начальной интенсивности менее чем на 1 % при использовании медианного и SG0 фильтров, соотношение WW / FWHM должно быть не более 0,2, фильтра SG2 – не более 0,9, фильтра SG4 – не более 1,6. Для контура лоренцевской формы и искажении начальной интенсивности полосы менее чем на 1 % в случае применения медианного фильтра и фильтра SG0 соотношение WW / FWHM должно быть менее 0,2, в случае фильтра SG2 – менее 0,7, фильтра SG4 – менее 1,1.

На рис. 4 приведены результаты исследования зависимости относительной полуширины (отношения FWHM после фильтрации к начальному параметру FWHM 0 ) от относительной ширины окна фильтров. Для обеспечения 1 % точности воспроизведения полуширины (см. рис. 4), относительная ширина окна фильтра должна удовлетворять таким же критериям, что и для искажения интенсивности полосы поглощения. Сравнивая результаты использования SG0 и медианного фильтров, можно прийти к выводу, что медианный фильтр искажает полуширину максимума меньше, чем фильтр SG0. При малых значениях относительной ширины окна влияние фильтра SG0 на интенсивность и полуширину полосы поглощения больше, чем у медианного фильтра, а фильтры SG2 и SG4 наиболее точно описывают контур полосы и меньше искажают его параметры. Отмеченные особенности можно использовать для выделения «полезного» сигнала и подавления сигнала «помехи» при решении задач прикладной спектроскопии.

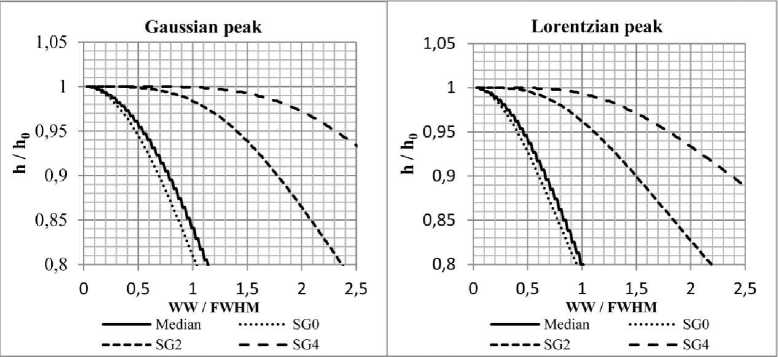
Рис. 3. Изменение относительной интенсивности полосы поглощения в зависимости от относительной ширины окна фильтров для изучения малых искажений

При решении ряда задач спектроскопии конденсированных сред для подавления полос поглощения, имеющих малую полуширину (спектры адсорбированных атомов и молекул, интерференционные полосы, полосы поглощения атмосферы), оптимальнее применять медианный фильтр или фильтр Савицкого–Голая нулевого–первого порядка.

Заключение

Анализ полученных в работе результатов по численному моделированию влияния фильтрации на контуры и положение полос поглощения лоренцевской и гауссовской форм позволяет сформулировать следующие рекомендации по разделению сигналов на «полезный» и «помеху»:

Физика

• 1.    Для абсолютного подавления полос поглощения «помех» предпочтительно применение медианного фильтра, при этом для гауссовского контура ширина окна фильтра должна быть в 5 раз больше полной ширины на половине высоты подавляемой полосы поглощения, а для контура лоренцевской формы это соотношение должно быть более 20.

• 2.    Для уменьшения искажения интенсивности полосы поглощения менее чем на 1 % можно рекомендовать выбирать относительную ширину окна фильтров для гауссовской формы контура и применении медианного фильтра – 0,2, SG0 – 0,2, SG2 – 0,9, SG4 – 1,6.

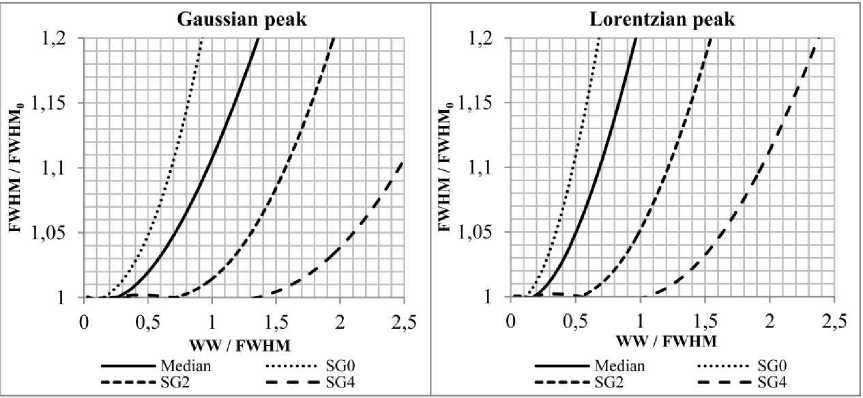
Рис. 4. Изменение относительной полуширины контура поглощения FWHM в зависимости от относительной ширины окна фильтров

Для лоренцевской формы контура и медианного фильтра это соотношение должно быть не более 0,2, для фильтров SG0 – 0,2, SG2 – 0,7, SG4 – 1,1.

Полученные в данной работе результаты моделирования влияния параметров оконных фильтров на положение полос поглощения лоренцевской и гауссовской форм, их интенсивность и полуширину, актуальны при исследовании объектов методами спектроскопии поглощения, излучения, зеркального и диффузного отражения, а также Рамановской спектроскопии.