Выбор параметров протеза стремени при стапедопластике на основе собственных частот

Слух – восприятие звуковых колебаний, которое осуществляется органами слуха. Слуховая система связывает приемник звука с мозгом. Слуховой аппарат человека состоит из проводящей и воспринимающей звук частей. Звуковые волны от внешнего источника поступают в наружный слуховой проход через ушную раковину. Когда они достигают конца слухового прохода, то заставляют вибрировать барабанную перепонку – кожаную мембрану, натянутую на конце слухового прохода. Эта вибрация, в свою очередь, заставляет колебаться три маленькие слуховые косточки – молоточек, наковальню, стремечко, расположенные в среднем ухе (рис. 1). Во время вибрации слуховые косточки отрабатывают сложную кинематику движения. В зависимости от величины звукового давления стремя двигается вперед и назад, вращается относительно продольной оси и поворачивает овальное окно – границу между средним и внутренним ухом. Эти движения вызывают вибрацию жидкости, которой заполнено внутреннее ухо. Вибрация жидкости улавливается эпителиальным образованием – кортиевым органом, являющимся частью спирали улитки [4, 7] .

Селянинов Александр Анатольевич, д.т.н., профессор кафедры теоретической механики, Пермь

Еловиков Алексей Михайлович, к.м.н., заведующий кафедрой отоларингологии, Пермь

Подгаец Роман Михайлович, к.т.н., профессор кафедры теоретической механики, Пермь

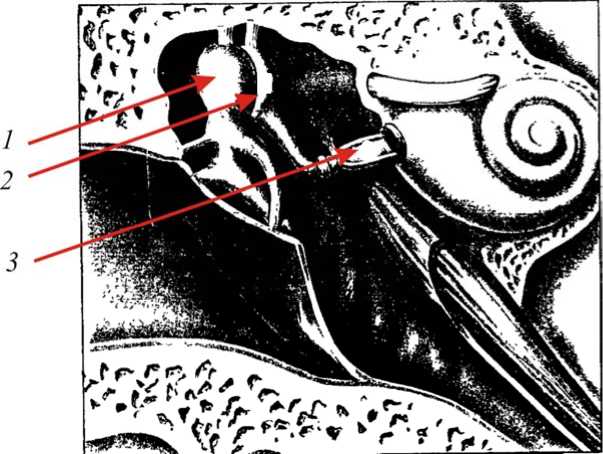
Рис. 1. Среднее ухо: 1 –молоточек, 2 – наковальня, 3 – стремя

Существуют заболевания, вызванные механическим повреждением или ограниченной подвижностью цепи косточек, которые могут привести к полной потере слуха. Операционный микроскоп, ювелирные методики операций, специальные хирургические инструменты – все это позволило вывести на новый, более высокий уровень хирургическое лечение заболеваний уха. Помимо удаления очага инфекции стало возможным сохранить больному слух, поэтому операция – радикальная слухосохраняющая. Более того, очень часто производят еще и слухоулучшающую операцию – тимпанопластику.

Тимпанопластика – это реконструкция разрушенного звукопроводящего аппарата (барабанной перепонки, слуховых косточек – молоточка, наковальни, стремени). Большую роль в развитии тимпанопластики сыграло детальное изучение анатомического строения среднего уха, функционального значения отдельных участков барабанной перепонки, слуховых косточек. Главным этапом тимпанопластики является замещение отсутствующей барабанной перепонки трансплантатом. Слуховые косточки заменяют общим протезом, соединяющим трансплантат с овальным окном.

В одной из последних теоретических работ по частотному анализу восстановленной колебательной системы, состоящей из искусственной барабанной перепонки и двух шарнирносоединенных между собой стержней [6], было исследовано влияние механических и физических характеристик протеза на нижний спектр частот в случае жесткого и упругого крепления восстановленной мембраны на внешнем контуре.

В ряде случаев отосклеротический процесс поражает костный лабиринт внутреннего уха. Нормальная кость замещается губчатой, затем плотной костью, отличающейся по своему строению от нормальной. Очень часто при этом замуровывается основание стремени, оно становится неподвижным, что влечет за собой снижение слуха. Заболевание начинается исподволь, без всякой видимой причины. Вначале постепенно снижается слух и появляется шум в одном ухе, а затем в другом.

Во второй половине XIX века была сделана первая попытка улучшить слух при неподвижности стремени хирургическим путем. Удачных операций было мало, в большинстве случаев наступала глухота, развивалось гнойное воспаление внутреннего уха. Помимо операционных осложнений воспалительные процессы в среднем ухе могут привести к утрате части косточки стремени, что требует ее реконструкции.

Когда появились новые оптические системы, полимеры и антибиотики, отохирурги смогли разработать операции на стремени, приводящие к хорошим функциональным результатам. Наиболее эффективная из них – стапедэктомия со стапедопластикой , то есть удаление стремени и замена его протезом [5]. Операции на стремени сложны технически, но невелики по объему, и пациенты хорошо переносят их. Слух появляется сразу же после операции: больного привозят в операционную глухим, а в палату он возвращается слышащим. В качестве материалов для протезов применяются тефлон, золото, платина, титан, нержавеющая сталь или гомотрансплантаты.

Первые частоты собственных колебаний стремени находятся в звуковом диапазоне 16 – 20000 Гц [8], что способствует лучшему восприятию определенных частей диапазона за счет резонансных явлений. Однако стременная косточка имеет сложную конфигурацию, повторять которую в виде протеза нецелесообразно.

В последние годы операции на стремени успешно производятся сотрудниками кафедры отоларингологии Пермской государственной медицинской академии имени академика Е.А. Вагнера. При этом имеет место проблема рационального выбора формы и материала протезов.

В качестве протеза стремени используются стержни постоянного и переменного сечения с крепежным элементом. В ходе операции стержень вставляется в отверстие, подготовленное в пластине овального окна. Передача колебаний наковальни к жидкости, заполняющей среднее ухо, осуществляется преимущественно путем продольных движений стержня, поэтому интересны продольные колебания протеза. В работе [9] показано, что в значительной части звукового диапазона слуховые косточки среднего уха движутся как абсолютно твердые тела, а начиная с 15 кГц – деформируются.

Поэтому следует исследовать собственные частоты продольных колебаний стержневых протезов. В силу малой длины стержневых протезов можно заранее предположить, что их первые собственные частоты попадают в сверхвысокочастотный диапазон. В МГц-диапазоне в непосредственной близости от человека работают системы сигнализации автомобилей и мобильные телефоны. Чтобы уменьшить вредное воздействие сверхвысокочастотных излучений на организм человека, следует вывести первые собственные частоты стержневых протезов стремени как можно дальше от нижнего предела МГц-диапазона.

Таким образом, в качестве критерия рационального выбора формы и материала стержневых протезов стремени можно предложить минимум первой собственной частоты.

Для этого предлагается доступная для специалистов в области отохирургии методика определения собственных частот и выбора наиболее подходящего материала и формы стержневых протезов стремени среднего уха человека.

Продольные колебания стержня постоянного сечения

Рассмотрим собственные колебания слуховых косточек на примере продольных колебаний стержня постоянного сечения (рис. 2) и найдем частоты этих колебаний.

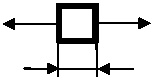
При продольных колебаниях каждый элементарный участок стержня длиной dx попеременно испытывает растяжение и сжатие, оставаясь плоским. Поскольку стержень относительно тонок, инерциальные силы в поперечном направлении, вызванные попеременным увеличением и уменьшением высоты сечения, пренебрежимо малы и можно считать, что инерционные силы в стержне направлены вдоль его продольной оси. Связь напряжений и перемещений, обусловленных только осевыми силами при малых колебаниях, _ ди            „ определяется законом Гука [3]: оx = Eгx = E—, где оx,гx,E,и - напряжение, деформация, дx модуль упругости и перемещение соответственно, причем координатная ось направлена вдоль оси стержня.

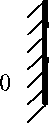
x

N

dN.

N +— dx 5x

dx

Рис. 2. Расчетная схема стержневого протеза стремени

Составим дифференциальное уравнение продольных колебаний стержня. Рассмотрим для этого элементарный участок стержня между поперечными сечениями, расположенными , ,,                                                                                                                   , 5и на расстоянии dx. На левой грани участка dx действует растягивающая сила N = EA— , где 5x

А – площадь сечения стержня, на правой грани кроме силы N имеется ее приращение д N

N +-- dx . Применяя второй закон Ньютона, получим д x

, , 52 и рAdx—т- =

5t2

где р есть плотность материала стержня.

Дифференциальное уравнение продольных колебаний стержня принимает вид рAdx —2- = — I EA— I dx, 5t2 5x (

5 ² и E 5 ² и

5 t ²    р 5 x ²

5 ² и _ 1 5 ² и 5 x ² a ² 5 1 ²

= 0,

= 0,

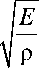
где а =

Частное решение этого дифференциального уравнения ищем в виде и ( x , t ) = X ( x ) T ( t ),

• т. е. предположим, что перемещение u можно представить в виде произведения двух функций, одна из которых зависит только от аргумента x , а другая – только от аргумента t . Тогда вместо определения функции двух переменных x и t необходимо определение двух функций X(x) и T(t) , каждая из которых зависит только от одной переменной.

Подставив выражение (2) в уравнение (1), получим а ² X"T = XT (штрихами обозначена операция дифференцирования по x ). Перепишем это уравнение в виде а ² X" / X = T / T . Для тождественного выполнения этого равенства (при любых x и t ) необходимо, чтобы каждая из частей была равна постоянной, которую обозначим через – p² :

• а ² X' '/ X = _ p ²; T / T = _ p ².

Отсюда следуют два уравнения:

T + p² T = 0; X '' + p 2 X = 0. a ²

Первое уравнение имеет следующее решение:

T = B sln( pt + a ),                                    (4)

указывающее на колебательный характер процесса. Из выражения (4) видно, что пока неизвестная величина p имеет смысл частоты свободных колебаний.

Второе уравнение из (3) имеет следующее решение:

( px A       ( px A

X = C sin l— 1 + D cos l— I                             (5)

• V a J       к a J

• и определяет собственную форму колебаний.

Частотное уравнение, определяющее величину p , составляется путем использования граничных условий. Это уравнение всегда трансцендентное и имеет бесконечное число корней. Таким образом, число собственных частот бесконечно, причем каждому значению частоты p n соответствуют своя функция T n ( t ), определяемая зависимостью (4), и своя функция X n ( x ), определяемая зависимостью (5).

Решение (2) является лишь частным и не дает полного описания движения. Полное решение получается путем наложения всех частных решений:

^

u = £ X , ( x )T ( t ).

n = 1

Функции X n ( x ) называются собственными функциями задачи и описывают собственные формы колебаний.

В случае если стержень закреплен одним концом, краевые условия имеют вид x = 0: X = 0 иx = l: X' = 0.                               (6)

Определим собственные частоты консольного стержня. Подставляя поочередно условия (6) в решение (5), получаем

D = 0; C — cos( pl / a ) = 0.

a

Условие C ^ 0 приводит к частотному уравнению

p cos — l = 0, a pl 2n -1

— =---- П.

a 2

Частота свободных колебаний, соответствующая n -й главной форме,

2 n - 1     2 n - 1

p„ =-----an =-----n n     2l

E

.

2 l ρ

Вычислим в рамках модели частоты собственных колебаний стержневых протезов стремени, изготовленных из костного материала, с характеристиками, близкими к реальному: E = 3 -109 Н/м2 (модуль упругости); А = 0,5 -10-6 м2 (площадь поперечного сечения); l = 3,5-10-3м (длина стремени); ц0 = 714,3-10-6кг/м (масса единицы длины стремени) [2, 5].

Также определим частоты собственных колебаний стержневых протезов стремени (табл. 2), выполненных из разных материалов ( l = 3,5 - 10 - 3 м), характеристики которых приведены в табл. 1.

Таблица 1

Характеристики материалов

Материал	р , кг/м3	E , 10 9 Па
Тефлон	920	5,5
Золото	19,3∙103	79
Платина	21,5∙103	160
Титан	4,5∙103	116
Нержавеющая сталь	(7,7–7,9)∙103	195–205

Таблица 2

Собственные частоты протеза стремени в виде однородного стержня

Материал	p 1 (с–1)	p 2 (с–1)	p 3 (с–1)	p 4 (с–1)
Кость	650 365	1 950 435	3 250 506	4 550 577
Тефлон	1 097 335	3 290 893	5 484 450	7 678 008
Золото	908 002	2 723 085	4 538 168	6 353 251
Платина	1 224 313	3 671 699	6 119 084	8 566 469
Титан	2 278 634	6 833 592	11 388 549	15 943 507
Нерж. сталь	2 272 582	6 815 441	11 358 301	15 901 160

Результаты для костного материала даны в качестве дальней перспективы. Данные вычисления показывают, что собственные частоты стержневых протезов выше 100 кГц – за пределом звукового диапазона. Причем уже вторая частота для титана и нержавеющей стали попадает в МГц-диапазон, а четвёртая находится в нем для всех применяемых материалов. Собственные частоты – сверхвысокочастотные. По критерию минимума первой частоты лучшими материалами для стержневых протезов стремени являются золото и тефлон.

Применяемая форма протеза представляет собой однородный стержень постоянного или переменного сечения с головкой для крепления к наковальне. Для приближенного расчета собственных частот стержней переменного сечения рассмотрим метод Ритца.

Метод Ритца

Изложим основное содержание этого метода [1] в применении к расчету продольных колебаний неоднородного стержня, для которого функционал Остроградского–Гамильтона имеет вид t2 l

⁵ = И И < х ) Ш t i о L        VO t

dxdt ,

где ц ( х ) - погонная масса стержня

кг • с²

м2

A ( х ) - площадь поперечного сечения [м 2 ],

• у ( х, t ) - продольное смещение сечения стержня в момент t.

Интеграл по x , взятый в пределах от 0 до l от двух слагаемых в квадратных скобках, представляет соответственно кинетическую и потенциальную энергию рассматриваемой системы.

Подставим в функционал (8) y ( x , t ) = ф ( x ) sin ( pt + a ) . После интегрирования по t в пределах одного периода — получим ^p

l

5 = ^ЧМx )ф2 (x) Р p

2 p ₀

- ЕЛо' (x )] dx,

где ф ( x ) - действительная форма.

Сущность метода заключается в приведении вариационной задачи к задаче на разыскание экстремума функции многих независимых переменных. Такое приведение осуществляется путем отбора из всех возможных допустимых функций, на которых рассматриваются значения функционала, некоторого специального класса функций, зависящих от конечного числа сначала неопределенных параметров. Подстановка таких функций в выражение функционала превращает его в функцию этих параметров, экстремум которой может быть найден известными элементарными способами.

В методе Ритца значения функционала (9) рассматриваются на совокупности выражений вида

ф( x ) = ]Г aiф i (x),                                     (10)

i = 1

где a i - параметры, варьируя которые получаем класс допустимых функций, ф i ( x ) - базисные или координатные функции, специально выбираемые или задаваемые известные функции, удовлетворяющие, по крайней мере, геометрическим краевым условиям рассматриваемой задачи.

На совокупности функций (10) соответствующий функционал обращается в функцию n независимых переменных a i , i =1, 2,..., n, то есть

5(ф) = 5(a^a2,...,an), и его первая вариация

85 M = Z> 8a,. i=1 da i

Найдя значения параметров ai из уравнений d5

---= 0, i = 1, 2,^, n da i

• и подставив их в (10), получим приближенное решение поставленной задачи.

Поскольку функционалы, соответствующие дифференциальным уравнениям малых колебаний прямых стержней, являются квадратичными относительно ф ( x ) , уравнения (11) линейны относительно a 1 , a ₂,..., a _n . Они имеют вид, аналогичный уравнениям малых колебаний системы с конечным числом степеней свободы. Приравнивая нулю определитель системы (11), получим уравнение, из которого найдутся приближенные значения первых частот системы. Это уравнение – уравнение частот Ритца.

Таким образом, подставив в функционал (9) минимизирующую форму (10), обратим 5 в квадратичную форму параметров a i

	S (a„ ..., a n ) = p 2 j T a i a k - ^ U k a i a k , i , k = 1                      i , k = 1	(12)
где	T k - f PV , V k dx , U ik = \ eA v/v k' dx . 00	(13)
	Уравнения (11) примут вид
	( p1T 11 - U ,1 ) « 1 + ... + ( p1T 1 n - U 1 n ) a n = 0, ( p 2 T 1 - U 21 ) a 1 + ... + ( p 2 К. n - U 2 , ) a n - 0,

(p ² T, - U _A ) a, + ... + ( p ² T„„ - U „„) a = 0. n 1 n 11            nn nn n

Условие, при котором не все a i одновременно равны нулю, является уравнением частот Ритца:

2 T 11 p 2 T 21 p	- U 11    • - U 21    .	2 ..    T 1 np 2 ..   T 2 n p	- U 1 n - U 2 n	- 0.	(14)
2 Tn 1 p	- Un 1    .	2 ..   Tnnp	- Unn

Рассчитаем собственные частоты продольных колебаний для стержневого протеза постоянного сечения с крепежной головкой (рис. 3) методом Ритца при помощи программы MathCAD . Длина l = 3,5 мм, радиус головки R = 0,5 мм, толщина протеза b = 0,3 мм.

Площади сечения первой и второй частей :

A = b 2 ,

A ₂ ( x ) = 2 b^R ² - ( x - l + R ) 2 .

Погонная масса стержня

Pi =p b2, p2 (x) = 2ph^R2 -(x-l + R)2.

Форма колебаний

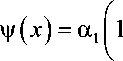
x l

2                      2223

I , x 1 x ( , x 1 x ( , x 1 x + a, 1 — —+ a, 1 — —;—ba, 1 — —;-.

² ( l J l 3 ( l J l ²       4 ( l J l ³

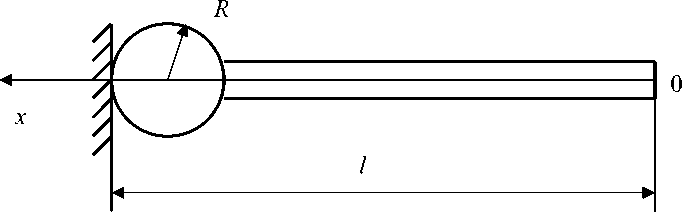
Рис. 3. Расчетная схема стержневого протеза стремени постоянного сечения с крепежной головкой

Каждый член этого разложения удовлетворяет краевым условиям задачи: x = 0: v"( 0 ) = v"( 0 ) = 0, x = l : ^ ( l ) = V‘ ( l ) = 0.

В первом одночленном приближении

U 11

2 b2 l-R1R -т     Л     >4           l           ___________________г     \4 T11 = - j    р b211 -—1 dx + j    2р b^R2-(x -1 + R )211 -—1 dx; 0        V l)          i,2                        V l) l - R-, R 2 l - R

R

. 2 b 2

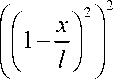
dx +

l l - R

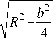
V

dx .

Из уравнения частот T11 р2 - UH = 0 находим верхнюю границу первой частоты для имплантата из тефлона:

p ₁ = 1 832 477 c^-1.

Для второго приближения берем в формуле (15) первые два слагаемых и получаем:

p1 = 1 381 543 c-1, p2 = 5 462 434 c-1.

Для третьего приближения р1 = 1381335 c-1, р2 = 3 854 569 c-1, р3 = 9 322 389 c-1.

Для четвертого приближения р1 = 1378 577 c-1, р2 = 3 834 006 c-1, р3 = 5 520 246 c-1, р4 = 14 050 672 c-1.

Аналогично вычисляем частоты для имплантата из золота. Результаты вычисления собственных частот приведены в табл. 3.

Четвертое приближение по первой собственной частоте мало отличается от третьего, и потому искать следующие приближения нет надобности.

В результате собственные частоты для такой формы протеза несколько выше частот, полученных для стержня постоянного сечения.

Таблица 3

Собственные частоты стержневого протеза стремени переменного сечения (рис. 3)

Приближение	Собственные частоты (с–1)
	Тефлон	Золото
Первое	p 1 = 1 832 477	p 1 = 1516 303
Второе	p 1 = 1381543 p 2 = 5 462 434	p 1 = 1143172 p 2 = 4 519 950
Третье	p 1 = 1381335 p 2 = 3 854 569 p 3 = 9 322 389	p 1 = 1143 001 p 2 = 3189 505 p 3 = 7 713 912
Четвертое	p 1 = 1378 577 p 2 = 3 834 006 p 3 = 5 520 246 p 4 = 14 050 672	p 1 = 1140 719 p 2 = 3172 489 p 3 = 4 567 787 p 4 = 11626 381

С целью упрощения изготовления и смещения центра тяжести стержневого протеза от области крепления к наковальне в сторону овального отверстия внутреннего уха рассмотрим собственные колебания протеза переменного сечения (рис. 4).

В этом случае площадь поперечного сечения А и погонная масса ц имеют вид

0 <  x <  l — R :

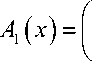
2 R — b l — R

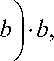
Pt (x ) = P b

2 R — b l — R

• x + b I;

R < x < l: A2 (x) = 2b^R2 —(x — l + R)2, ц2 (x) = 2pb^R2 —(x — l + R)2.

Результаты вычисления собственных частот приведены в табл. 4. Следует отметить хорошую сходимость метода Ритца для определения собственных частот, так как уже на четвёртом приближении первая собственная частота практически стабилизируется. Значения первой частоты протеза увеличились незначительно (в 1,029 раз по отношению к протезу на рис. 3, то есть небольшое утолщение протеза в области крепления к наковальне не ухудшает частотные характеристики в смысле минимума первой собственной частоты. Такой протез из тефлона более технологичен в изготовлении по сравнению с предыдущим, сделанным из золота.

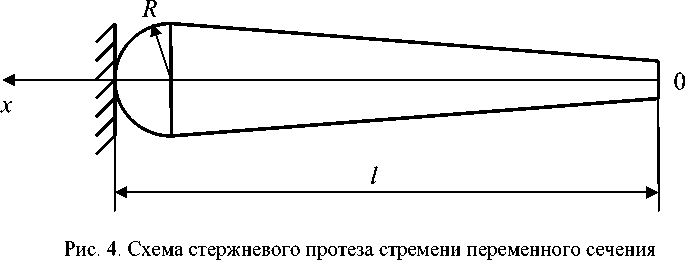
Таблица 4

Собственные частоты стержневого протеза стремени переменного сечения (рис. 4)

Приближение	Собственные частоты (с-1)
	Тефлон	Золото
Первое	p 1 = 1938912	p 1 = 1 604 374
Второе	p 1 = 1 497 287	p 1 = 1238946
	p 2 = 5018661	p 2 = 4152745
	p 1 = 1447905	p 1 = 1198085
Третье	p 2 = 3582728	p 2 = 2 964 567
	p 3 = 8754460	p 3 = 7 243 973
	p 1 = 1418628	p 1 = 1173 859
	p 2 = 3511039	p 2 = 2 905 248
Четвертое	p 3 = 5714187	p 3 = 4 728 266
	p 4 = 13276290	p 4 = 10985611

Выводы

• 1.    На основе приближенного метода Ритца разработана доступная методика оценки собственных частот продольных колебаний стержневых протезов стремени переменного сечения, применяемых при операциях стапедопластики среднего уха человека. Получена хорошая сходимость метода Ритца по первой собственной частоте.

• 2.    Показано,   что собственные частоты стержневых протезов находятся в

• 3.    С целью вывода первых собственных частот из МГц-диапазона введен критерий рациональной формы и материала стержневого протеза стремени – минимум первой собственной частоты. Данному критерию удовлетворяют стержневые протезы переменного сечения (см. рис. 4) из золота и тефлона, ввиду лучшей технологичности при изготовлении – из тефлона.

сверхвысокочастотном диапазоне, изменяются в пределах 30% при изменении формы сечения от постоянного по длине до переменного и сильно зависят от материала.

Благодарности

Авторы работы выражают искреннюю благодарность коллегам с кафедры теоретической механики Пермского государственного технического университета и заведующему кафедрой био- и наномеханики Белорусского государственного университета профессору Г.И. Михасеву за плодотворное обсуждение содержания данной работы.

Медицина, 1983. – 272 с.