Выбор параметров сетки конечных элементов при моделировании роста трещин гидроразрыва

Основной технологией интенсификации добычи углеводородов является гидроразрыв нефтяного пласта. Он производится путём закачивания в скважину жидкости под высоким давлением, что инициирует зародышевую трещину. Давление жидкости воздействует на берега трещины, заставляет её распространяться вглубь массива горных пород. Для поддержания трещины в открытом состоянии в жидкость гидроразрыва добавляют твёрдые частицы, так называемый проппант. После утечки жидкости в породу образуется высокопроницаемый канал для фильтрации нефти из пласта в скважину, что увеличивает объём добываемой нефти [1].

Перед математическими моделями гидроразрыва ставятся три взаимосвязанные задачи: 1) описать течение вязкой жидкости в трещине; 2) рассчитать упругую деформацию породы; 3) определить возможность распространения трещины и направление. Две последних задачи составляют предмет механики деформируемого твёрдого тела. При численной реализации модели гидроразрыва актуально наличие совершенных вычислительных технологий решения каждой из перечисленных задач. Особенно следует выделить методы расчёта напряженно-деформированного состояния породного массива, учитывающие распространение трещины с выбором направления её роста [2].

2.    Модель Христиановича–Гиртсмы–де Клерка (KGD)

Трещина гидроразрыва моделируется плоским разрезом бесконечной высоты (Рис. 1), погружённым в линейно-упругую изотропную среду и ориентированным перпендикулярно направлению действия горизонтальных напряжений σ ₀ , порождённых боковым стеснением пород [3, 4]. Такое представление справедливо при допущении, что высота трещины значительно превосходит ее длину 2 l ( t ). В трещину закачивается ньютоновская жидкость с постоянным расходом Q ₀ , в результате чего трещина распространяется прямолинейно вдоль оси x согласно теории линейной механики хрупкого разрушения. Предполагаются выполненными условия плоской деформации.

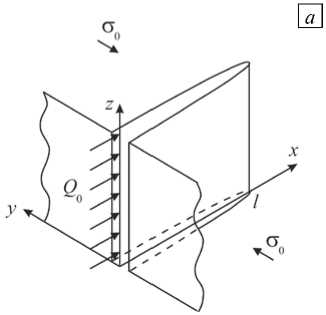
Рис. 1. KGD модель трещины гидроразрыва ( а ); вид в плане ( б )

Пусть w ( x ) — раскрытие трещины, p_f ( x ) — давление жидкости, p ( x ) = p_f ( x ) - σ ₀ — избыточное давление жидкости на берега трещины. В случае плоской деформации раскрытие прямолинейной трещины в бесконечной плоскости связано с величиной давления на её берегах следующим соотношением [5]:

4 ^l w ( x ) =       p ( s )ln

π E ′ ₀

'J l ² - x ² + 'J l ² - s ² l ² - x ² - V l ² - s ²

ds ,

при этом E ′ = EI (1 -ν ²) , E — модуль Юнга, ν — коэффициент Пуассона. В качестве критерия начала роста трещины примем силовой критерий разрушения Ирвина [6]

K I = K Ic

где K _I — коэффициент интенсивности напряжений (КИН) для трещины нормального отрыва, который для симметричной трещины можно представить в виде [5]:

K _I = 2 J; dx , π 0 l ² - x ²

K _Ic — критическое значение КИН или вязкость разрушения — константа материала, представляющая способность материала сопротивляться распространению трещины. Критерий (2) можно записать также как асимптотику раскрытия трещины в её вершине

w ( x ) = lim x → l

8 K Ic

2πE′

l - x .

3.    Компьютерное моделирование

Появление приближенных численных методов анализа задач механики разрушения обусловлено значительными трудностями, связанными с нахождением аналитических решений даже для простых геометрий и условий нагружения. Среди численных методов решения линейных и нелинейных задач исследования трещин наибольшее распространение получил метод конечных элементов (МКЭ). Многими исследователями обсуждалось применение МКЭ к решению специфических задач механики разрушения, в этом направлении был проделан значительный объём работы. Предложено большое количество различных видов специальных конечных элементов, которые учитывают сингулярность поля напряжений в окрестности вершины трещины. Типичными недостатками этих элементов является либо несовместимость с обычными элементами, либо неспособность отображать перемещение тела как жёсткого целого. Из-за ограниченной пригодности компьютерных программ, содержащих эти специальные элементы, в приложениях МКЭ к задачам механики разрушения, как правило, приходится иметь дело со стандартными элементами, доступными в большинстве общецелевых программ МКЭ. Наиболее используемы элементы с линейной аппроксимацией смещений (при постоянной деформации) и квадратичной аппроксимацией смещений (при линейной деформации). Исследования показывают, что для достижения с помощью этих элементов приемлемых решений требуется высокая степень измельчения сетки, особенно при линейных элементах, и кроме того, точность решения существенно зависит как от размеров и формы элементов, так и от общей конфигурации сетки. Например, в окрестности вершины трещины требуются очень мелкие элементы, но для того, чтобы уменьшить количество узлов сетки общепринятым способом, необходимо увеличить размеры элементов далеко от трещины. Существуют разные методы сгущения сеток и, следовательно, разные группы исследователей, работающие независимо друг от друга, в рамках одной и той же задачи механики трещин, вероятно, построят множество разных по виду сеток. К сожалению, эти сетки могут привести в результате к очень разным решениям. Факты показывают, что конфигурация, по крайней мере, относительно грубых сеток оказывает значительное влияние на точность вычислений, хотя всё еще не сделано исчерпывающих выводов о взаимосвязи сеточных свойств и точности вычислений.

В последнее время находит распространение так называемый расширенный метод конечных элементов (X-FEM), предложенный в работах Беличко [7–9]. Этот метод устраняет трудности при решении задач с локализованными сингулярностями, которые не эффективно реализуются традиционным МКЭ. X-FEM можно использовать в задачах, связанных с проблемой сингулярности в вершине трещины, где локальные особенности адекватно описываются соответствующей комбинацией базисных функций. В стандартном МКЭ при аппроксимации негладких решений требуется осторожность при построении сетки. Например, узлы сетки должны совпадать с точками разрывов, и сетку необходимо измельчать вблизи точек с большим градиентом поля напряжений. В отличие от этого X-FEM способен достичь оптимальной скорости сходимости на структурированных сетках, где присутствуют произвольные разрывы решений.

В расчётах КИН, особенно прямыми методами, большое влияние на точность результатов оказывает выбор сетки конечных элементов. Значительное число различных сеток для вычисления K _I опробовано в работе [10]. Для нескольких простых задач механики разрушения с помощью элементов с линейной и квадратичной аппроксимацией смещений изучалось влияние сеточных параметров на точность получаемых решений с целью выработки руководящих принципов для оптимизации сетки конечных элементов. Точность МКЭ решений оценивалась путём сравнения вычисленного КИН с его величиной, найденной аналитически. Естественно, что [10] — это довольно ограниченное исследование, поскольку рассмотрено небольшое число элементарных проблем с хорошо документированными аналитическими решениями. Тем не менее в работе даются следующие практически значимые рекомендации:

• 1.    Размер элементов в окрестности вершины трещины должен быть мал по сравнению с длиной трещины. Для элементов с линейной аппроксимацией смещений оптимальный размер таких элементов равняется 1 200 длины трещины.

• 2.    В области с характерным размером порядка длины трещины размеры элементов должны плавно возрастать.

• 3.    Отношение длины любого элемента к его ширине не может превышать 50.

Работа [10] на долгие годы стала фактическим стандартом (руководством) для многих исследователей проблем линейной механики разрушения. Сделанные в ней выводы и рекомендации вошли во многие справочники, учебники и монографии по численному решению задач механики хрупкого разрушения методом конечных элементов (см., например, [11, 12]). Недостаток этой работы или, вернее, неполнота исследования заключается в том, что авторы ограничились изучением трещин только на краях пластин, причём равномерно распределённая нагрузка прикладывалась к внешнему контуру пластины, сами же трещины были свободны от напряжений. Цель данного исследования заключается в попытке восполнить этот пробел, поскольку в задачах гидроразрыва нефтяного пласта давление закачиваемой в трещину жидкости действует на берега трещина, вызывая её распространение.

Рассмотрим пластину единичной толщины с размерами в плане 200 х 200 м, находящуюся в условиях плоской деформации. Пластина содержит центральную внутреннюю прямолинейную трещину длиной 2 1 = 20 м. Трещину моделируем как двусторонний разрез, к берегам которого приложено нормальное давление p ( x ). Внешние границы пластины свободны от напряжений. Геометрия пластины представлена

100 м
	100 м
НИН 10м	100 м

а

б

Рис. 2. Геометрия расчётной области ( а ); пример сетки конечных элементов ( б )

на рисунке 2 а . Вследствие симметрии только правая половина пластины покрыта сеткой конечных элементов, ось O y является осью симметрии (Рис. 2 б ). Материал пластины изотропный линейно упругий с модулем Юнга E = 24600 МПа и коэффициентом Пуассона v = 0,25. Расчёт напряжённо-деформированного состояния пластины выполнялся в пакете конечно-элементного анализа MSC.Marc 2012 [13].

Опробовано большое число сеток из прямоугольных элементов с линейной и квадратичной аппроксимацией смещений. Размеры четырёх ближайших к вершине трещины элементов, которые всегда были квадратными, принимались равными h = 0,4, 0,1, 0,025 м. Сгущение узлов сетки к вершине трещины производилось в горизонтальном направлении (по оси O x ) и по двум вертикальным: от верхней грани пластины к вершине трещины и от нижней грани так же к вершине трещины (см. Рис. 2 а ). Отношение размеров (расстояний между узлами) элементов у вершины и на границе области задавалось равным 1:25, 1:50, 1:100. На берегах трещины имело место либо равномерное разбиение, либо незначительное сгущение: 1:2,5; 1:5. На рисунке 2 б , показана сетка конечных элементов с параметрами: h = 0,4 м, сгущением к вершине 1:25 и сгущением на берегах трещины 1:2,5.

На берегах трещины считались известными следующие модельные распределения нормального давления:

Р 1 ( x ) = 1,

p 2 ( x ) = ¹ — 1 X 0,

Р з ( x ) = 10,

Р 4 ( x ) =    ^- 1 x 0,

Р 5⁽ x ) = ²

-

x

-

x

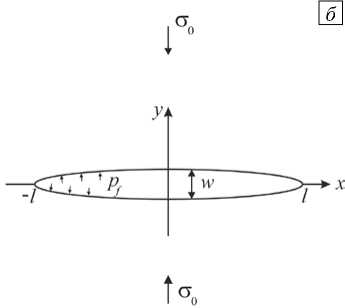
Профили давления (5) названы модельными, поскольку они использовались в предварительных тестовых расчётах для отработки вычислительной методики КИН. Профиль p ₁ соответствует постоянному давлению на берега трещины; профили p ₂ , p ₃ — линейные, причём к вершине трещины давление p ₂ падает до нуля, а давление p ₃ возрастает; профили p ₄ , p ₅ описывают квадратичное и кубическое распределение давлений соответственно, причём для профиля p ₅ имеется участок отрицательного давления на берега трещины. Эпюры давлений (5) представлены на рисунке 3. Также приводятся профили давлений p ₆ , p ₇ , взятые из реальных гидродинамических совместных задач течения жидкости в трещине гидроразрыва [14, 15]. Для профиля p 7 полудлина трещины составляет l = 100 м, полуширина пластины — 1000 м.

Коэффициент интенсивности напряжений K _I определим с помощью инвариантного J -интеграла [16], который в случае плоской деформации связан с K I соотношением JE' = K I ². Вычисление J -интеграла в пакете MSC.Marc базируется на методе Делорензи [17] (другое название — метод интегрирования по областям), согласно которому контурный интеграл преобразуется в интеграл по площади (см. с. 144 в [13]), интегрирование ведется по кольцу элементов, окружающих вершину трещины, напряжения находятся в точках гауссова интегрирования, располагающихся внутри элементов. Такое обобщение J -интеграла позволяет использовать его при решении геометрически и физически нелинейных задач и расширить применение на случай температурных деформаций, массовых сил и давления на берегах трещин.

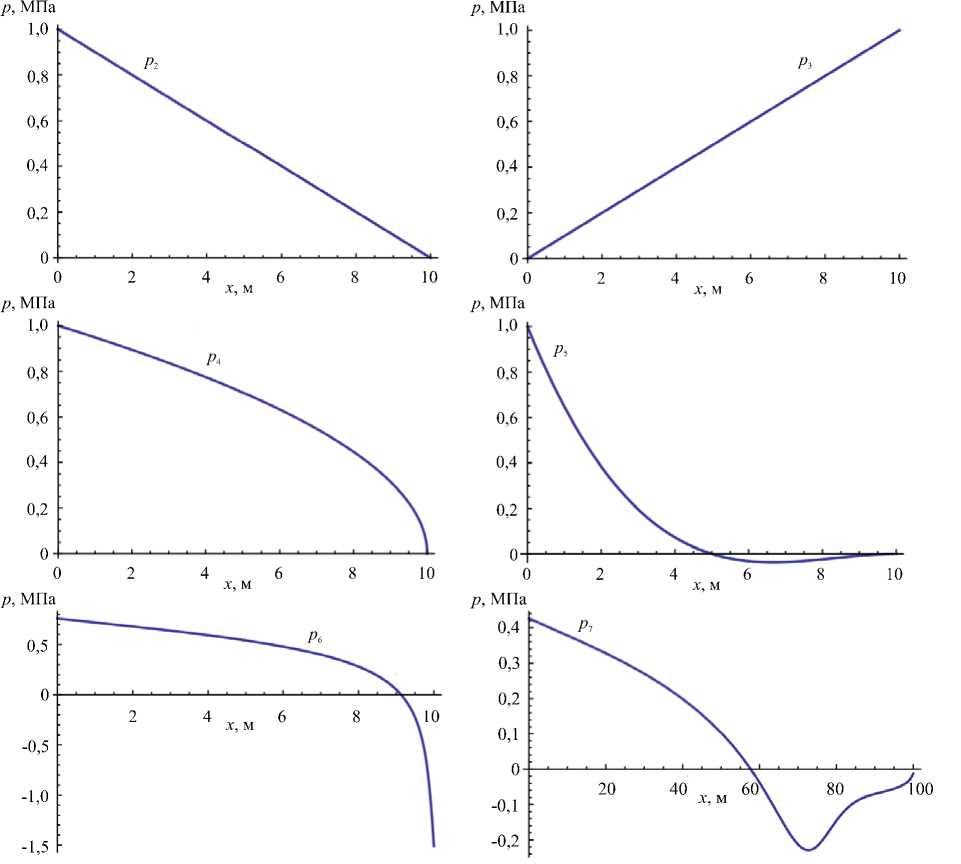
Рис. 3. Эпюры давлений на берегах трещины

В обсуждаемых ниже примерах область интегрирования состоит из 8-ми вложенных друг в друга колец элементов, окружающих вершину трещины, причём начиная с 4-го или 5-го значение J -интеграла практически не изменяется. Результаты расчёта при разных профилях давления показаны на рисунке 4. По оси абсцисс отложено отношение полудлины трещины l к размеру конечного элемента у вершины трещины h : точки с координатами 25, 100, 400 соответствуют линейным конечным элементам с размерами h = 0,4,0,1, 0,025 м, точка 800 условно обозначает элементы с квадратичной аппроксимацией смещений с размером у вершины h = 0,025 м. По оси ординат отложен нормированный коэффициент интенсивности напряжений K t I — отношение вычисленного значения K I к точному. Точное значение K I находится по формуле (3) с учётом поправки на конечные размеры пластины (для пластины, у которой отношение длины трещины к ширине пластины составляет 0,1, поправочный коэффициент, согласно справочнику [18], равняется 1,014). Интегрирование в формуле (3) выполняется численно с помощью процедуры NIntegrate компьютерной программы Mathematica 8.0.

Для постоянного профиля давления p ₁ при минимальном размере элемента ошибка составляет: e min = 1,09 %. Профили p ₂, p 3 — линейные, при этом давление p ₂ убывает к вершине трещины (см. Рис. 3), e min = 0,77 %, а давление p 3 возрастает, поэтому погрешность становится заметно больше: e min = 2,18 %. По виду квадратичный профиль давления p ₄ аналогичен асимптотике раскрытия трещины у её вершины (4), поэтому вычисления КИН при нём демонстрируют наименьшую ошибку: e min = 0,33 %. Анализ полученных результатов обнаруживает общую тенденцию: наибольшая погрешность наблюдается в тех расчётах, где давление возрастает с приближением к вершине трещины. Для кубического профиля p ₅

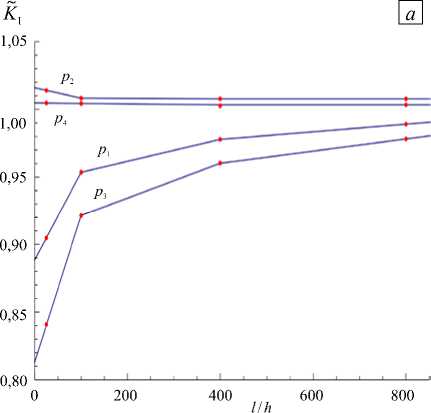
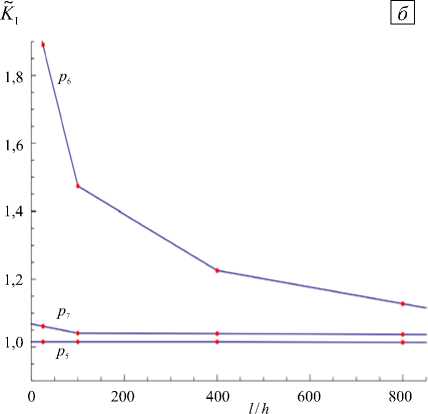
Рис. 4. Зависимость нормированного КИН от размеров элементов для профилей давления p ₁,..., p ₄ ( а ); p ₅,..., p ₇ ( б ) давление с приближением к вершине трещины падает до нуля, поэтому даже грубая сетка даёт высокую точность результатов e min = 1,34%.

Крайне неудовлетворительные результаты демонстрирует расчёт КИН при профиле p ₆ , в соответствии с которым давление резко падает, достигая значительных отрицательных величин в окрестности вершины трещины: на грубой сетке ошибка достигает 88,86%, на мелкой — e min = 12,77 %. Подобный профиль давления является характерным в задачах гидроразрыва нефтяного пласта; резкое падение давления объясняется неоднородностью утечек жидкости в пласт через боковую поверхность трещины. Для профиля p ₇ отрицательное давление уменьшается почти до нуля в вершине трещины, поэтому погрешность вычислений вполне приемлемая: e min = 3,7 %. В задачах гидроразрыва давление закачанной жидкости создает распределённую нагрузку на стенки трещины, и в этом случае крайне важно иметь точные значения приложенных к берегам трещины нормальных напряжений. Следовательно, необходимо строить достаточно мелкую стеку конечных элементов не только в окрестности вершины трещины, но и по всей её поверхности.

С целью уточнения решения для профиля давления p ₆ была сконструирована сетка конечных элементов со следующими параметрами: размером ближайших к вершине трещины элементов h = 0,005 м, отношением 1/h = 2000; сгущением узлов сетки вблизи вершины трещины в горизонтальном направлении и к берегам трещины по двум вертикальным направлениям 40:1, а также вдоль берегов трещины 10:1; общим числом четырёхугольных элементов 165259. В результате удалось снизить ошибку в определении КИН с 12,77% до 10,7% при четырёхугольных элементах с линейной аппроксимацией смещений и до 6,44% при четырёхугольных элементах с квадратичной аппроксимацией смещений.

4.    Моделирование распространения трещины

Рассмотрим распространение трещины гидроразрыва на примере давления с профилем p ₇ (Рис. 3), действующего на берега трещины полудлиной l = 100 м в пластине полушириной 1000 м (Рис. 2 а ). На рисунке 5 показано раскрытие трещины (кривая 1 ), полученное на сетке конечных элементов со следующими параметрами: отношением l/h = 400; размером элементов у вершины h = 0,25 м; сгущением узлов к линии распространения трещины 100:1; сгущением на берегах трещины 4:1, разбиением с равномерным шагом h = 0,25 м вдоль линии распространения трещины; общим числом прямоугольных элементов с линейной аппроксимацией смещений 1400450. Для сравнения на рисунке 5 представлено аналитическое решение для раскрытия трещины на бесконечной плоскости (кривая 2 ), вычисленное по формуле (1).

Моделирование распространения трещины будем проводить в статической постановке, без учёта движения жидкости, то есть предполагаем, что продвижение трещины происходит под действием постоянного во времени давления p ₇ , приложенного к берегам трещины на участке от 0 до 100 м. Тогда зависимость КИН K _I от длины трещины, вычисленная по формуле (3) с учётом поправки на конечные размеры пластины (см. с. 340 в [18]), примет вид, показанный на рисунке 6. Согласно рисунку, КИН

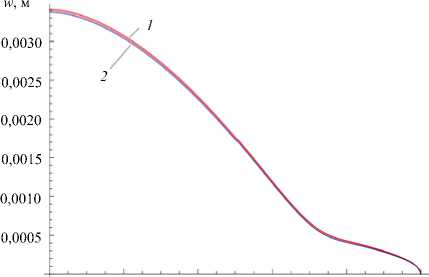
О 20        40        60        80       100

х, м

Рис. 5. Эпюры раскрытия трещины: численный расчёт (кривая 1 ); точное решение ( 2 )

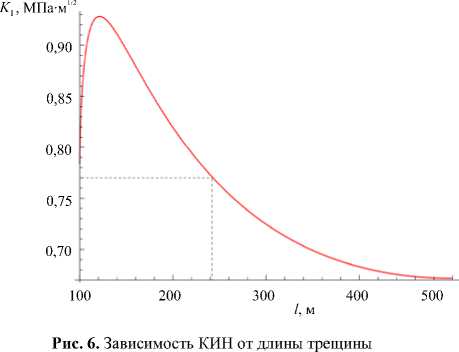
сначала возрастает, достигая максимума, а затем монотонно убывает, следовательно, минимальная длина, на которую может распространиться трещина, составит l = 228,5 м. Если принять критический КИН равным K I c = 0,769МПа^м¹ / ² [19-21], то тогда точное решение для профиля давления p 7 даст минимальный размер трещины l = 243,8 м.

Процесс распространения трещины в линейно-упругом изотропном теле можно охарактеризовать интенсивностью освобождения упругой энергии G , которая в МКЭ вычисляется с помощью методики виртуального закрытия трещины VCCT [22]. Данный метод опирается на следующие гипотезы: 1) энергия, требуемая для разделения поверхностей, равняется энергии, необходимой для смыкания этих же поверхностей; 2) напряжённое состояние вокруг вершины трещины существенно не изменится, когда трещина подрастёт на малую величину. Концепция квазихрупкого разрушения Гриффитса [6] основывается на энергетическом балансе энергии деформации тела и работы, затрачиваемой на образование новой поверхности. Энергетический критерий Гриффитса можно записать в виде:

G = - dW = Gc , da

где W — энергия деформации, a — длина трещины.

Дадим пояснения к формуле (6). Критерий G зависит от геометрии тела и приложенных нагрузок, а параметр G_c называется вязкостью разрушения и является характеристикой материала, определяемой из экспериментов. Интенсивность освобождения упругой энергии G не связана со временем, а характеризует скорость изменения потенциальной энергии тела в зависимости от изменения длины трещины. Уравнение (6) представляет собой критерий разрушения: трещина начинает расти, когда G достигает критического значения G_c .

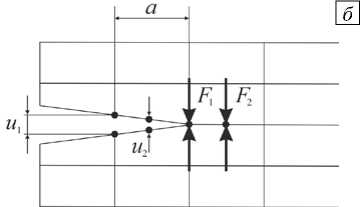
Рассмотрим простейшую конечно-элементную модель, содержащую трещину нормального отрыва (Рис. 7 а ). В методе VCCT значение G вычисляется как G = Fu/ (2 a ), где F — силы, удерживающие берега трещины вместе, u — раскрытие трещины в ближайших к её вершине узлах. Для элементов с квадратичной аппроксимацией перемещений необходимо учитывать вклад промежуточных узлов (Рис. 7 б): G = ( Fu 1 + F ₂ u ₂)/ ( 2 a ) .

Задачу распространения трещины решим в геометрически нелинейной постановке [23] с учётом образования новых поверхностей. Давление с профилем p ₇ действует на берегах первоначальной трещины полудлины l = 100 на участке от 0 до 100 м, по времени давление возрастает линейно от 0 до 1 (здесь под временем, как принято в квазистатических задачах, понимается некоторый монотонно возрастающий безразмерный параметр нагружения). Вязкость разрушения G_c вычислим по формуле: Gc = K I ² c IE' = 2,254 ■ 10 ^{- 5} МН/м, где K I c = 0,769 МПа^м¹ / ².

В силу симметрии как приложенных нагрузок, так и геометрии пластины относительно оси O x , трещина распространялась прямолинейно (по I-й моде разрушения) с расщеплением граней элементов. Расчёт вёлся с постоянным шагом по времени 0,01; в момент времени 0,95 (что соответствовало уровню нагружения 95%) трещина начала распространяться и за 250 итераций достигла длины 286,75 м; интенсивность освобождения упругой энергии составила G = 2,246 ■Ю^{- 5} МН/м и оказалась меньше критического значения. Поэтому трещина остановилась. На следующем шаге, при нагрузке 96% от максимальной, трещина «прострелила» до конца пластины.

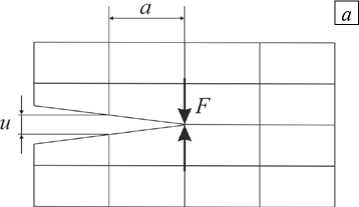
Рис. 7. Метод виртуального закрытия трещины: линейные элементы ( а ), квадратичные элементы ( б )

Заметим, что минимальная длина трещины l = 286,75 м, полученная при решении квазистатической задачи, заметно больше длины l = 243, 8 м для статического случая. Объясняется это тем, что, во-первых, в квазистатическом приближении использовались общие уравнения механики деформируемого твёрдого тела [23] с учётом геометрической нелинейности, а не уравнения линейной механики разрушения (1)–(4), и, во-вторых, метод конечных элементов даёт завышенные значения интенсивности освобождения упругой энергии [13].

5.    Заключение

Первый важный вывод состоит в том, что, по крайней мере для рассмотренных элементарных сингулярных задач, метод конечных элементов с линейной аппроксимацией перемещений сходится к решению, которое для всех практических целей является точным. Определённая минимальная ошибка в пределах точности инженерных расчётов (3–5%) обуславливается главным образом неточностями, связанными с непрямыми методами определения КИН, а не слабостью самого по себе МКЭ. На протяжении всего исследования демонстрируется, что точность решения чувствительна к конфигурации сетки. Следующий вывод заключается в существовании нескольких параметров, определяющих эффективность построения конечно-элементных сеток, и эти параметры устанавливаются, а именно минимальный размер элемента, расстояние между узлами в окрестности вершины трещины, степень удлинённости отдельных элементов. Все рекомендации по их выбору, приведённые в [10], остаются в силе, но их число необходимо дополнять и расширять в задачах с заданным профилем давления на берегах трещины. Выводы относительно характеристик, которые должны быть присущи эффективным сеткам, следующие:

• 1.    Необходимо, чтобы размеры элементов, непосредственно примыкающих к вершине трещины, были достаточно малыми по сравнению с длиной трещины, безотносительно к тому, какой метод применяется для вычисления КИН. По-видимому, у таких элементов существует оптимальный размер, который составляет примерно 0,0025 l .

• 2.    Сгущение следует осуществлять плавно путём увеличения расстояния между узлами во всех направлениях, начиная с минимального расстояния у вершины трещины. Размер области сгущения равен длине трещины (сгущение N :1 , число элементов не менее N , то есть размер элемента на границе области в N раз больше размера элемента у вершины трещины, а число элементов вдоль линии, по которой производится сгущение, не менее N ). За границами зоны плавного увеличения расстояния между узлами, по-видимому, нет явного ограничения на размеры элементов.

• 3.    Сильно вытянутые элементы даже в удалённых от вершины трещины местах сетки приводят к заметной погрешности. Для достижения приемлемых результатов соотношение размеров отдельных элементов не должно превышать 50.

• 4.    В задачах гидроразрыва давление закачанной жидкости создаёт распределённую нагрузку на стенки трещины, поэтому крайне важно иметь точные значения приложенных к берегам трещины нормальных напряжений, следовательно, необходимо строить достаточно мелкую сетку конечных элементов не только в окрестности вершины трещины, но и по всей включающей её поверхности.

• 5.    Моделирование распространения трещины целесообразно проводить с помощью VCCT (Virtual Crack Closure Technique) — методики виртуального закрытия трещины, а в качестве критерия разрушения выбирать энергетический критерий Гриффитса, причём сгущение сетки проводить к линии возможного распространения трещины. В случае криволинейной траектории трещины прибегать к локальной перестройке сетки в окрестности вершины трещины по мере её распространения.

Используя эти выводы как руководство к конструированию эффективных сеток КЭ, можно достигнуть высокой точности оценки КИН либо интенсивности освобождения упругой энергии G в задачах, подобных рассмотренным.

Следует подчеркнуть, что поскольку обсуждались довольно простые задачи, пока нет достаточных оснований считать перечисленные рекомендации верными и в общем случае. Приведёт ли их выполнение к таким же хорошим результатам в более сложных задачах, можно определить только путём численных экспериментов.

Работа выполнена при финансовой поддержке РФФИ (проект № 14-08-00113).