Выборочное распределение наблюдений числа падения кукурузной муки

Проведение эмпирических исследований предусматривается для установления статистических закономерностей измеряемой величины, количественно характеризующей исследуемый вариационный признак, а саму «…измеряемую в испытаниях величину рассматривают как случайную…», распределение которой соответствует теоретическому закону. Отмечается, что «…если изучаемый признак измеряется физическими методами, то его можно рассматривать как непрерывную случайную величину с неизвестной функцией распределения по заданному алгоритму» [1]. На практике возникает задача установления по экспериментальным данным закона распределения измеренной случайной величины путем выбора модели, адекватно ее описывающей: «…в результате в качестве наиболее вероятного закона для исходной выборки выбирается тот, для которого значение функции распределения будет максимальным» [2]. Получив нормальное распределение наблюдаемой случайной величины, далее прибегают к проверке гипотезы относительно параметров распределения генеральной совокупности, т. е. к проверке основной гипотезы, проверяемой при помощи критериев согласия. Считается, что «…критерии согласия позволяют определить вероятность того, что при гипотетическом законе распределения наблюдающееся в рассматриваемой выборке отклонение вызывается случайными причинами, а не ошибкой в самой гипотезе. Если такая вероятность велика, то отклонение от гипотетического закона распределения следует признать случайным и считать, что гипотеза о предполагаемом законе распределения не опровергается… Вероятностный характер критериев согласия позволяет утверждать, что гипотеза не противоречит данным опыта в случае, если вероятность наблюдаемого отклонения от гипотетического закона распределения велика, и напротив, если эта вероятность мала, то статистическая гипотеза не согласуется с опытными данными» [3].

Объект данного исследования – наблюдения числа падения кукурузной муки, являющейся рецептурным компонентом хлебобулочных изделий [4–12], в том числе с диетической направленностью [13–16], в мировой практике выступает как статистический материал для получения референсных (интервальных) значений показателя числа падения крахмалистых растительных ресурсов [17, 18] с надлежащей точностью метода при коэффициенте вариации не выше 1,4–1,7%. Однако представленные в указанных работах результаты не содержат убедительное доказательство проверки статистической гипотезы о равенстве средних двух выборок, на основании которых можно сделать выводы о необходимости проведения серии опытов с целью достижения желаемых интервальных значений измеряемой величины. В подобных экспериментах «…внутривидовая вариация определяет степень различия между средними в двух группах, тестируемых неоднократно…» [19], что характерно для зависимых выборок. Отсюда значительная часть внутригрупповой изменчивости в обеих группах объясняется авторами индивидуальными различиями субъектов при исключении ранее обнаруженной вариации. Для чистоты опыта укажем, что в перечисленных процедурах в качестве нулевой гипотезы рассматривается предположение о том, что средние в группах равны при выявлении зависимости между группируемой и зависимой переменными при требуемом уровне значимости p .

Целью данной работы явилось изучение выборочного распределения наблюдений числа падения кукурузной муки для определения репрезентативности выборки опытных данных. Определение параметров функции распределения случайной величины, получаемой по выборке, позволяет сравнить их с таковыми для генеральной совокупности, распределенной по теоретическому закону. С помощью теоремы Гливенко ранее доказано, что при достаточно большой выборке случайной величины, сгруппированной в вариационный ряд, «…функцию распределения генеральной совокупности приближенно можно заменить выборочной функцией распределения» [3] в случае преобразования выборочных данных в статистический ряд.

В связи с этим, вместо полного определения случайной величины в виде закона распределения вероятностей прибегают «…к установлению числовых характеристик – вещественных чисел, выражающих характерные особенности случайной величины и относимые к ее моментам» [3]. Начальный момент первого порядка оказывается математическим ожиданием (или средним значением) случайной величины. Первый центральный момент всегда равен нулю, а второй центральный момент является дисперсией, квадратный корень из которого стандартом или средним квадратичным отклонением. Третий центральный момент, разделенный на стандарт в кубе, служит коэффициентом асимметрии, а четвертый центральный момент, разделенный на стандарт в четвертой степени, соответственно, коэффициентом эксцесса. Указанные моменты относят к общим (интегральным) характеристикам распределения, но немаловажную роль для описания характеристик случайной величины отводят и квантилям, т. е. значениям, которые заданная случайная величина не превышает с фиксированной вероятностью.

Материалы и методы

Материалом исследования послужил промышленный образец кукурузной муки тонкого помола, соответствующего требованиям ГОСТ 14176–69 [20] (ПФ «Радуга», ст. Северская, Краснодарский край). Показатели качества кукурузной муки соответствовали требованиям, представленным в таблице 1. Число падения изучали при реализации стандартного метода на приборе ПЧП-99 и определяли как «…время, необходимое для перемешивания водно-мучной суспензии мешалкой и ее падения с верхнего до нижнего положения в вискозиметрической пробирке» при нагревании и клейстеризации суспензии в кипящей водяной бане [21].

Для проведения исследования выборочных данных наблюдений числа падения кукурузной муки применили метод «сгруппированных данных» для получения интервального вариационного ряда с показателями центра распределения (выборочная средняя, мода, медиана, квартили, децили), показателями вариации (размах, среднее линейное отклонение, дисперсия, несмещенная оценка дисперсии, среднее квадратичное отклонение, коэффициент вариации, линейный коэффициент вариации, коэффициент осцилляции), показателями формы распределения (относительный показатель квартильной вариации, коэффициент асимметрии, структурный коэффициент асимметрии Пирсона, показатель эксцесса), показателями интервального оценивания центра генеральной совокупности (доверительные интервалы для генерального среднего, интервальное оценивание генеральной доли, т. е. вероятности события). Для изучаемой случайной величины числа падения кукурузной муки гипотезу о нормальном распределении проверяли с помощью показателей асимметрии и эксцесса, а также при применении правила т рех сигм. Изучение вариационного интервального ряда для выборочных данных производили в онлайн-калькуляторе «Показатели вариации» .

Результаты

Исходные экспериментальные данные, преобразованные в интервальный вариационный ряд, сведены в таблицу 2. Рассчитанные характеристики интервального вариационного ряда (показатели центра распределения, вариации и формы распределения) приведены ниже. Расчет средней взвешенной (выборочной средней) произведен по формуле (1), моды – по формуле (2), медианы – по формуле (3), квартилей – по формулам (4, 5), децилей – по формулам (6, 7), среднего значения по способу моментов – по формуле (8), среднего квадрата отклонений по способу моментов – по формуле (9), среднеквадратичного отклонения – по формуле (10), размаха вариации – по формуле (11), среднего линейного отклонения – по формуле (12), дисперсии – по формуле (13), несмещенной оценки дисперсии – по формуле (14), оценки среднеквадратичного отклонения – по формуле (15), коэффициента вариации – по формуле (16), линейного коэффициента вариации – по формуле (17), коэффициента осцилляции – по формуле (18), коэффициент асимметрии – по формуле (19), среднеквадратичной ошибки коэффициента асимметрии – по формуле (20), структурного коэффициента асимметрии Пирсона – по формуле (21), коэффициента эксцесса – по формуле (22), среднеквадратичной ошибки коэффициента эксцесса – по формуле (23), доверительного интервала для генерального среднего – по формуле (24), стандартной ошибки выборки для среднего – по формуле (25), предельной ошибки выборки – по формуле (26), доверительного интервала для генеральной доли – по формуле (27). Проверку статистической гипотезы о принадлежности выборочных данных наблюдений числа падения кукурузной муки нормальному распределению наблюдений генеральной совокупности производили исходя из выполнения условия (28) и правила 3σ (29).

Таблица 1.

Требования к показателям качества кукурузной муки по ГОСТ 14176–69 [20]

Requirements for quality indicators of corn flour according to GOST 14176–69 [20]

Table 1.

Показатель | Indicator	Характеристика | Characteristics
Цвет | Colour	Белый или желтый | White or yellow
Запах | Flavour	Свойственный кукурузной муке, без посторонних запахов, не затхлый, не плесневелый Characteristic of corn flour, odorless, not musty, not moldy
Вкус | Taste	Свойственный кукурузной муке, без посторонних привкусов, не кислый, не горький Characteristic of corn flour, without foreign flavors, not sour, not bitter
Минеральная примесь | Mineral impurity	При разжевывании муки не должно ощущаться хруста When chewing flour, there should be no crunch
Влажность, %, не более | Moisture, %, no more	15,0	15,0	15,0
Зольность в пересчете на сухое вещество, %, не более | Ash content in terms of dry matter, %, no more	0,9	1,3	–
Жир в пересчете на сухое вещество, %, не более | Fat in terms of dry matter, %, no more	2,5	3,0	–
Крупность помола: | Fineness of grinding:
остаток на сите из шелковой ткани № 23 по ГОСТ 4403, не более the residue on the silk fabric sieve No. 23 according to GOST 4403, no more	2		2
остаток на сите из проволочной сетки № 56 по ТУ 14–4–1374, не более the residue on the wire mesh sieve No. 56 according to TU 14–4–1374, no more	–		–
проход через сито из шелковой ткани № 32 по ГОСТ 4403, не менее passage through a silk fabric sieve No. 32 according to GOST 4403, at least	30	–	30
Металломагнитная примесь, мкг в 1 кг муки Metallomagnetic admixture, mcg in 1 kg of flour размером отдельных частиц в наибольшем линейном измерении не более 0,3 мм и (или) массой не более 0,4 мг, не более the size of individual particles in the largest linear dimension is not more than 0.3 mm and (or) the mass is not more than 0.4 mg, not more	3	3	3
размером и массой отдельных частиц более указанных выше значений the size and mass of individual particles are more than the above values	Не допускается Not allowed
Зараженность вредителями хлебных запасов | Pest infestation of grain stocks
Загрязненность вредителями вредных запасов | Pest contamination of harmful stocks

x =

Средняя взвешенная (выборочная средняя):

I xf I f

333,5-3 + 338 • 6 + 342-7 + 345,5-2 + 349.5-2

6812,5

= 340,625

Выбираем в качестве начала интервала 341, так как именно на этот интервал приходится наибольшее количество, определили, что наиболее часто встречающееся значение ряда – 341,333.

Медиана служит характеристикой при асимметричном распределении данных, т. к. при наличии их «выбросов» более устойчива к воздействию отклоняющихся из них:

Мода как наиболее часто встречающееся значение признака у единиц данной совокупности:

M о = x о + h

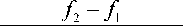
⁽ f 2 ^- f 1 ^{) + (} f 2 ^- f i )

= 341 + 2

7 - 6

(7 — 6) + (7 — 2)

= 341,333,

h f I f     1

M e = ^x 0 '      । ;     S me - 1 I =

f me V            У

2< 20

= 341 + - -° - 9 = 341,286 .

71 2 J

где x 0 – начало модального интервала; h – величина интервала; f 2 – частота, соответствующая модальному интервалу; f 1 – предмодальная частота; f 3 – послемодальная частота.

Медианным является интервал 341–343, т. к. в этом интервале накопленная частота S больше медианного номера. Медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот. Расчет показал, что 50% единиц совокупности будут меньше по величине 341,286.

Таблица 2.

Характеристики интервального вариационного ряда наблюдения числа падения кукурузной муки

Table 2.

Characteristics of the interval variation series of observation of the falling number of corn flour

Интервал Interval	Сер. интервала, х центр Middle of interval, х сеntrе	Количество, f i Quantity, f i	Х I ·f i	Накопленная частота, S Accumulated frequency, S	|x-х ср |·f i	(x-х ср )2·f i	Относительная частота, f i /f Relative frequency, f i /f
331–335	333,5	3	1000,5	3	21,375	152,297	0,15
336–340	338	6	2028	9	15,75	41,344	0,3
341–343	342	7	2394	16	9,625	13,234	0.35
344–347	345,5	2	691	18	9,75	47,531	0,1
348–351	349,5	2	699	20	17,75	157,531	0,1
Итого | Total		20	6812,5		74,25	411,938	1

Квартили, как значения признака в ранжированном ряду распределения, выбраны таким образом, что 25% единиц совокупности меньше по величине квартиля Q 1 , 25% будут заключены между квартилями Q 1 и Q 2 , 25% – между квартилями Q 2 и Q 3 , а остальные 25% превосходят квартиль Q 3 :

h | ^Z f )- Q 1 = x 0 ⁺^l^^ S me - 1 I = f me

4 <20

= 336 + - -°- 3 = 337,333 ,

61 4 J

3hf3 •z Л     V

Q3 = x0 ■      ।     --- Sme-1 I = fme

2<3-20

= 341 + - —⁰ - 9 = 342,714 .

71  4      J

Расчет показал, что 25% единиц совокупности меньше по величине 337,333, квартиль Q 2 совпадает с медианой и равен 341,286, а остальные 25% превосходят значение 342,714.

Децили, как значения признака в ранжированном ряду распределения, выбраны таким образом, что 10% единиц совокупности меньше по величине дециля D 1 , а 80% заключены между децилями D 1 и D 9 , а остальные 10% превосходят дециль D 9 .

h f^ f

^D1 = ^X 0 ⁺ z- l ,       S me -1

fme V

= 332 + 3 -0 - 0 = 334, 3110 J h f 9 z fi

D g = X q +-----

^{9    0} f I 10

me

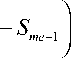
3 ( 9-20

= 344 + ³ 1 — - 16 1 = 347.

3 1 10      J

Расчет показал, что 10% единиц совокупности меньше по величине 334, а остальные 10% превосходят 347.

Среднее значение изучаемого признака по способу моментов равно:

X = -Ah + A = ——3 + 342 = 340,625 (8)

I f,          20              ’ где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой), равен 501; h – шаг интервала, равен 26.

Средний квадрат отклонений по способу моментов равен:

Г x ' П f               2

D = L - J ^J- h ² + ( X - A )² =

I f,       ⁽      )                   (9)

49.97 . ,

= -^-3 2 - ( 340,625 - 342 ) = 20,597.

Результаты расчета квадрата отклонений по способу моменту приведены в таблице 3.

Таблица 3.

Расчет квадрата отклонений по способу моментов

Table 3.

Calculation of the square of deviations by the method of moments

x ц	x * i	x * i f i	[ x * i ]2 f i
333,5	-2,8333333333333	-8,5	24,083333333333
338	-1,3333333333333	-8	10,666666666667
342	0	0	0
345,5	1,1666666666667	2.3333333333333	2,7222222222222
349.5	2,5	5	12,5
		-9,1666666666667	49,972222222222

Среднеквадратичное отклонение равно: о = DD = 720,597 = 4,538.      (10)

Соответственно, каждое значение ряда отличается от среднего значения 340,625 в среднем на 4,538.

Размах вариации как разность между максимальным и минимальным значениями признака первичного ряда:

• — = xmax - xm-n = 351 - 332 = 19.(11)

Среднее линейное отклонение для учета различия всех единиц исследуемой совокупности равно:

Z| x, - xf74,25

d = —!!— =-----= 3,713.(12)

I f      20,

Очевидно, что каждое значение ряда отличается от другого в среднем на 3,713.

Дисперсия как мера разброса около ее среднего значения (мера рассеивания, т. е. отклонения от среднего) равна:

If x, - x )2 f   411,938

D =    --- LA =--- ,938 = 20,597. (13)

I f       20

Результат аналогичен полученному ранее по формуле (9).

Несмещенная оценка дисперсии как состоятельная оценка дисперсии (исправленная дисперсия) равна:

S 2 = ^{I (} x - x ) ^f = 411,938 = 21,681.   (14)

I f - 1        19       ,

Оценка среднеквадратичного отклонения равна:

s = S^ = 7 21,681 = 4,656.

Коэффициент вариации, как мера относительного разброса значений совокупности, показывает, какую долю среднего значения этой величины составляет ее средний разброс:

о v = —

x

4,538

340,286

100% = 1,33%.

Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая, поэтому полученным результатам можно доверять.

Линейный коэффициент вариации характеризует долю усредненного значения признака абсолютных отклонений от средней величины:

K = d = ^3,713 100% = 1,09%.     (17)

^d x 340,625

Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней:

R 19

K = - =------ 100% = 5,58%.     (18)

^r x 340,625

Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. Наиболее точным и распространенным показателем асимметрии является моментный коэффициент асимметрии:

As = MJs ³—.7^ = 0,243,         (19)

• ³     4,538^{3     ,    ,}

где M 3 – центральный момент третьего порядка;

s – среднеквадратичное отклонение.

Полученная положительная величина моментного коэффициента асимметрии указывает на наличие правосторонней асимметрии.

Оценка существенности показателя асимметрии дается с помощью среднеквадратичной ошибки коэффициента асимметрии:

6 ( ^и - 2)        I 6(5 - 2)

= w ) x = 0,612.   (20)

( n + 1 )( n + 3 )   )|( 5 + 1 )( 5 + 3 )

Если выполняется соотношение | As |/ s A s < 3, то асимметрия несущественная, ее наличие объясняется влиянием различных случайных обстоятельств.

Если имеет место соотношение | As |/ s A s > 3, то асимметрия существенная и распределение признака в генеральной совокупности не является симметричным. Результаты расчета центральных моментов приведены в таблице 4.

Таблица 4.

В анализируемом вариационному ряду распределения наблюдается несущественная асимметрия (0,243 / 0,612 = 0,4 < 3).

Структурный коэффициент асимметрии Пирсона характеризует асимметрию только в центральной части распределения, т. е. основной массы единиц, и не зависит от крайних значений признака:

Если отношение Ex/s E х > 3, то отклонение от нормального распределения считается существенным. В данном случае s E х < 3, поэтому

отклонение от нормального распределения считается не существенным.

Доверительный интервал для генераль-

ного среднего равен:

_ x - M ₀_ 340,625 - 341,333 _

-A™ —          —                     — 0,16.     ⁽²¹⁾

sp      о           4,538

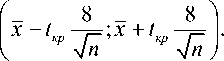
Коэффициент эксцесса определяется для симметричных распределений, при этом эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения:

Для проведения расчета определили значение t kр по таблице распределения Стьюдента: T табл ( n -1; α / 2) = T табл (19; 0,025) = 2,433.

Стандартная ошибка выборки для сред-

него равна:

E x — M- — 3 — s

s 4,656

^c n     20

— 1,0412.       (25)

1078,95

4,5384

- 3 — 2,5433 - 3 — - 0,46.

Для распределений более островершинных (вытянутых), чем нормальное, показатель эксцесса обычно положительный ( Ex > 0), для более плосковершинных (сплюснутых) – отрицательный ( Ex < 0), т. к. для нормального распределения выполняется равенство M 4 / s ⁴ = 3. Число 3 вычитается из отношения μ ⁴/ σ ⁴, поскольку для нормального закона распределения μ ⁴/ σ ⁴ = 3, поэтому для нормального распределения эксцесс равен нулю.

Для данного вариационного ряда характерно плосковершинное распределение при выполнении условия Ex < 0. Существенность эксцесса рассчитывается по статистике Ex/s E х , где s E х – средняя квадратическая ошибка коэффициента эксцесса:

Стандартная ошибка среднего указывает, на какую величину среднее выборки 340,625 отличается от среднего генеральной совокупности.

Предельная ошибка выборки равна:

54.656

s — tKp^ — 2,4334656 — 2,533.(26)

кр n20

или если ε = t kр , то s с = 2,433 ∙ 1,041 = 2,533.

Расчетный доверительный интервал равен: (340,625 – 2,533; 340,625 + 2,533) = (338,092;

343,158). С вероятностью 0,95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.

Доверительный интервал для генеральной доли ( p · - ε; p · + ε ) равен:

s — t кр

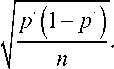
24n(n - 2)(n - 3)

Ex   ^( n +1)2 (n + 3)( n + 5)

-----3---------— — 0,5.

(5 +1) (5 + 3)(5 + 5)

В рассматриваемом случае принято равенство 2 Ф ( t kр ) = γ. Ф ( t kр ) = γ / 2 = 0,954 / 2 = 0,477. По таблице функции Лапласа нашли t kр значение при Ф ( t kр ) = 0,477, т. е. t kр ( γ ) = (0,477) = 2. Результаты вычислений приведены в таблице 5.

Расчет центральных моментов

Table 4.

Calculation of central moments

Интервал | Interval	Середина интервала, х центр | The middle of the interval, х сеntrе	Количество, f i | Quantity, f i	(x-х ср )3·f i	(x-х ср )4·f i
331 – 335	333,5	3	-1085,115	7731,446
336 – 340	338	6	-108,527	284,884
341 – 343	342	7	18,197	25,021
344 – 347	345,5	2	231,715	1129,61
348 – 351	349,5	2	1398,09	12408,047
Итого | Total		20	454,359	21579,009

Таблица 5.

Интервальное оценивание генеральной доли

Table 5.

Interval estimation of the general share

Доля i -ой группы f i /∑ f The share of the i -th group f i / ∑f	Средняя ошибка выборки для генеральной доли, ε Average sampling error for the general fraction, ε	Нижняя граница доли, p · - ε Lower limit of the share, p · - ε	Верхняя граница доли, p · + ε Upper limit of the share, p · + ε
0,15	/ 0,1571 - 0,15) s = 2 U—1--- ’—L = 0,0798 20            ,	0,0702	0,23
0,3	/ 0,371 - 0,3) s = 2,—( ---,^ = 0,1 20	0,198	0,402
0,35	/ 0,35 • ( 1 - 0,35 ) s = 2 J  --- = 0,11 20	0,243	0,457
0,1	1 0,1 ( 1 - 0,1 ) s = 2,            = 0,0671 20	0,0329	0,167
0,1	/ 0,1 ( 1 - 0,1 ) s = 2,            = 0,0671 20	0,0329	0,167

С вероятностью 0,954 при большем объеме выборки эти доли будут находиться в заданных интервалах.

При проверке статистической гипотезы о том, что случайная величина наблюдений числа падения кукурузной муки распределена по нормальному закону, воспользовались следующим условием:

| As | < 3 S as ; | A | < 3 S As ; | E | < 3 S ex (28)

Для изучаемого вариационного ряда S аs = 0,6124, S ех = 0,5, As = 0,243, Ex = -0,46. |0,243| < 3×0,6124 = 1,8371; |-0,46| < 3×0,5 = 1,5, то есть 3σ условия выполняются.

При проверке статистической гипотезы о том, что случайная величина наблюдений числа падения распределена по нормальному закону с помощью правила 3σ, воспользовались предположением: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднеквадратичного отклонения, т. е. все значения случайной величины должны попасть в интервал:

x - 3

В рассматриваемом случае этот интервал составил: (340,625 – 3 · 4,538; 340,625 – 3 · 4,538) = (327,011; 354,239), все значения случайной величины попадают в интервал, так как х min = 332, х mах = 351.

Очевидно, что для рассматриваемой выборки небольшого объема (n = 20) при проверке статистической гипотезы о законе распределения достаточно было использовать критерий

Стьюдента для сравнения генеральных параметров распределения и их оценок, полученных по выборке. В качестве оцениваемых параметров выборки целесообразным посчитали выбирать центральные моменты.

Обсуждение

Полученные в работе результаты совпадают с принятыми представлениями о параметрах функции распределения, определяемых с помощью методов статистического анализа эксперимента. В целях статистического анализа в математической статистике введено понятие абстрактной генеральной совокупности, состоящей из всех допустимых значений случайной величины, и выборки, представляющей собой совокупность ограниченного числа значений, полученных в результате опытов [3, 19, 22]. В соответствии с этим, различают выборочные характеристики случайной величины, найденные по ограниченному числу наблюдений и зависящие от этого числа, и соответствующие им характеристики генеральной совокупности. Предметом подобного изучения служит репрезентативная выборка, т. е. выборка, в которой все основные признаки генеральной совокупности, из которой извлечена данная выборка, представлены приблизительно в той же пропорции или с той же частотой, с которой данный признак выступает в этой генеральной совокупности. По изучаемой выборке наблюдений числа падения кукурузной муки в виде интервального вариационного ряда (таблица 2) рассчитали широкий перечень выборочных статистических характеристик, которые и явились оценками соответствующих генеральных параметров (таблица 5).

Заключение

Изучение выборочного распределения наблюдений числа падения кукурузной муки позволило установить числовые характеристики, выражающие характерные особенности случайной величины и относимые к ее центральным моментам. Статистический метод «сгруппированных данных» для получения интервального вариационного ряда с показателями центра распределения, вариации, формы распределения и интервального оценивания центра генеральной совокупности позволил оценить репрезентативность выборочных данных в отношении варьирования изучаемого признака в генеральной совокупности. Статистическая гипотеза о нормальном распределении изучаемой случайной величины числа падения кукурузной муки доказана путем расчета показателей асимметрии и эксцесса (соответственно, третьего и четвертого центральных моментов), а также при применении правила 3σ. В силу взятого объема выборки (n = 20) при проверке статистической гипотезы о законе распределения достаточно было использовать критерий Стьюдента для сравнения генеральных параметров распределения и их оценок, полученных по выборке.

Исследования выполнялись с использованием оборудования ЦПК «Исследовательский центр пищевых и химических технологий» КубГТУ (СКР_3111), развитие которого поддерживается Министерством науки и высшего образования РФ (Соглашение № 075–15–2021–679).