Вычисление и анализ собственных функций ограниченного радиально-симметричного оператора распространения в свободном пространстве в ближней зоне

Затухающие электромагнитные волны являются одним из основных объектов изучения оптики ближнего поля. Известно, что вклад волн такого типа становится значительным, когда размер объекта или расстояние порядка длины волны и меньше. До появления ближнепольных микроскопов значение затухающих волн игнорировалось в оптике [1-4]. Стоит отметить, что ближнепольная микроскопия не является единственным объектом изучения оптики ближнего поля. С учетом затухающих волн были разработаны различные теоретические подходы [5-12] и алгоритмы расчета [13-17].

Увеличение интервала пространственных частот – является главной идея оптики ближнего поля. Данный механизм обеспечивает сохранение затухающих компонент поля источника и преодоление таким образом дифракционного предела [18-26].

Стоит отметить, что за пределами ближней зоны дифракции, также существует возможность преодоление дифракционного предела [27]. В частности, при острой фокусировке достигается компактная локализация лазерного излучения. Однако, в этом случае требуется амплитудная или фазовая аподизация зрачка оптической системы [28-32], использование специальных типов поляризации [33-35] или внесение фазовой сингулярности в пучок [36, 37], а также сочетания всех этих факторов [38-41] с целью оптимизации формируемого поля [42-45].

Однако вне зоны ближнего поля уменьшение размера светового пятна, как правило, сопровождается значительным ростом боковых лепестков [27, 45-47], в то время как на расстоянии менее длины волны не имеется каких-либо ограничений на размер светового пятна – локализация лазерного изучения может быть сколь угодно малой, хотя существенно зависит от размера деталей фокусирующего элемента [48-50] или воздействующих пучков [51-53].

В данной работе с помощью разложения по плоским волнам исследуется распространение осесимметричных лазерных пучков в ближней зоне дифракции (на расстояние порядка длины волны). Характеристики сигналов (информации), передаваемой без потерь (без искажения) опре- деляются, как собственные функции такого оператора, имеющие собственные значения близкие к единице. В работах [54, 55] показана необходимость численного расчета собственных функций. Это связано с ограниченностью оператора распространения как в пространственной, так и спектральной областях. В рамках данной работы выполнен расчет осесимметричных собственных функций ограниченного оператора распространения в ближней зоне дифракции и проведены исследования качественных и количественных характеристик в зависимости от расстояния распространения и ограничений, наложенных в объектной и спектральной областях.

1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

”     ,     -------V2п                                 I

E ( р , 9 , z ) = jexp I- kz Vct ² - 11 1 j F ( ст , ф )exp [ ik рст cos( 9-ф ) ] d ф 1ст d CT . (5) /(J

Проанализируем часть в (5), зависящую от полярного угла. Экспоненциальный множитель по модулю равен единице. Спектральная функция F ( ст , ф ) (при фиксированном f) убывает не медленнее, чем 1/ ст , иначе не будет выполняться равенство Парсеваля. Таким образом, интегрирование по углу даст функцию, которая не возрастает с ростом s, и для дальнейшего анализа её можно заменить на константу:

г                                         1

I = exp - kz4 ст² - 1 ст d ст =----т-

^{J Р(}                )           ( kz )² .

Абсолютная погрешность при замене верх-

него предела на конечное значение ст _z :

Скалярный непараксиальный оператор рас-

пространения с использованием разложения по плоским волнам записывается следующим образом [16, 17]:

У ^ст 2^{2 - 1} ₊    ¹

^{( kz ) 2}

exp ( - kz^ ст 2 - 1 ) ,

E ( u , v , z ) = J J F ( 5 , n )exp ( ikz 4 1 -5 2 -П 2 ) exp [ ik ( ^ u + n v ) ] d ^ d n , ^{2 5}

F fe n ) = F JJ ^E 0 ( x , y ) exp [ - ^ik 6 ^{x +} n y ) ] d x ^d y                  ,

X

² O

где F (x,h) – спектр разложения входного поля по плоским волнам, 2 _$ : ст , <  -J 5 2 + n ² <ст ₂ — область учитываемых пространственных частот. При ст , = 0, ct ₂ = 1 рассматриваются только распространяющиеся волны, а при ст , = 1, ст ₂ >  1 - только затухающие волны.

В случае, когда входное поле является осесимметричным:

E о ( x , y ) = E о ( r ),                  (2)

выражение (1) можно упростить:

относительная погрешность:

s=^A = ( kz J ст 2 - 1 + 1 ) exp ( - kz^ ст 2 - 1 ) .    (8)

Величина e монотонно убывает с ростом ст _z (можно доказать, взяв производную). Сделав замену t = kz^ ст z - 1, получим функцию, не зависящую от определённых значений X и z . Для нахождения допустимой границы отсечения нужно задаться определённой погрешностью e и решить уравнение (8).

В частности, для e = 0,04 получаем t = 5, т.е. выбор в качестве верхней границы частот:

к 5 У²

ст z =11^1+ 1 .                  (9)

V V kz )

.ст I СТ . I

E ( р , z ) = - ik ² J J e_o ( r ) J_o ( k ст r ) r d r exp 0 V 0                        )

( ikz 71 —CT ² ) J ₀ ( k стр ) ст d ст , (3)

где r – радиальная координата в выходной плоскости, ст - радиальная координата в частотной плоскости, ст ₀ - радиус учитываемых пространственных частот.

При численной реализации по теореме Найквиста ст ₀ определяется дискретизацией входного поля A r :

обеспечивает погрешность расчёта (5) не выше 5%.

Перепишем оператор (3) в виде:

r o

E ( р , z ) = J E o ( r ) K ( r , p , z ) rdr ,        (10)

где

K ( r , р , z ) = - ik ²

^ст 0

ст d ст .(11)

^CT 0

X

2 A r •

Распространяющимся волнам соответствуют пространственные частоты, расположенные в круге радиусом ст ₀ <  1. Чтобы учесть также и затухающие волны, вносящие свой вклад на расстояниях меньше длины волны, необходимо увеличивать радиус учитываемых пространственных частот до некоторого значения ст _z >  1 , зависящего от расстояния z от апертуры. Оценим это значение.

Рассмотрим интеграл (1) в полярных координатах только в области затухающих волн:

Тогда задача вычисления осесимметричных собственных функций в ближней зоне дифракции сводится к поиску собственных функций следующего ограниченного оператора:

^r 0

bn ^{( z} ) V n ( р , ^z ) = J V n ( ^r ) ^K ( ^r , р , ^z ) ^rdr , (12)

где z - расстояние, b_n ( z ) - собственные значения, v _n ( р , z ) - собственные функции.

Очевидно, характеристики собственных функций будут зависеть не только от расстояния распространения z , но и от ограничений, наложенных на поле в объектной и спектральной областях.

• 2.    РАСЧЕТ ОСЕСИММЕТРИЧНЫХ СОБСТВЕННЫХ ФУНКЦИЙ ОГРАНИЧЕННОГО ОПЕРАТОРА

РАСПРОСТРАНЕНИЯ В БЛИЖНЕЙ ЗОНЕ ДИФРАКЦИИ

Расчет собственных значений и собственных функций был выполнено для различных значений параметров при тестовой длине волны лазерного излучения X = 1 ц m .

На рис. 1 показан вид матриц (11), являющихся ядром преобразования (12), а на рис. 2 -вид рассчитанных матриц упорядоченных собственных векторов для различных параметров.

Как видно из рис. 1, 2 сужение области пространственных частот (уменьшение значения s0) приводит к заполнению матрицы ядра преобразования ненулевыми значениями. В этом случае расчет собственных векторов усложняется (рис. 2б).

На рис. 3 показаны графики полученных собственных значений. Видно, что при расстояниях меньше длины волны и при учете затухающих волн |а| >  1 (рис. 3а) график собственных значений имеет классический вид, близкий к ступенчатой функции. Если значительно увеличить расстояние при учете только распространяющихся волн |а| <  1 (рис. 3б), то собственных значений, близких к единице становится значительно меньше.

На рис. 4 показаны нормированные графики полученных собственных функций. Так как функции в общем случае комплексные, то показана только действительная часть. Из рисунка 4 видно, что собственные функции в первом случае имеет классический вид, а во втором – вырожденный. Чтобы улучшить ситуацию, нужно увеличить размер входной области.

Рис. 1. Амплитуда матриц (11), являющихся ядром преобразования (12) для

(а) r = 10 X , z = 0.5 X , ^ о = 10, (б) r = 10 X , z = 20 X , ^, = ¹

a) b)

Рис. 2. Вид рассчитанных матриц (амплитуда, негатив) упорядоченных собственных векторов для

(а) r = 10 X , z = 0.5 X , ^ 0 = 10, (б)

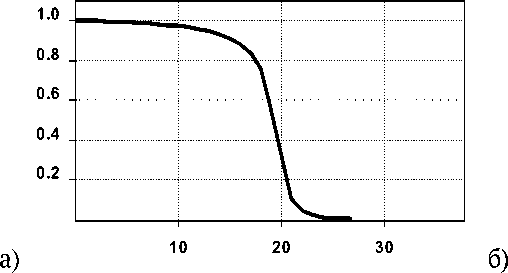
Рис. 3. График модулей собственных значений b_n ( z ) для (а) r₀ = 10 X , z = 0.5 X , g ₀ = 10, (б) r = 10 X , z = 20 X , ^ 0 = ¹

r ₀ = 10 X , z = 20 X , g ₀ = 1

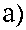
r, мкм

б)

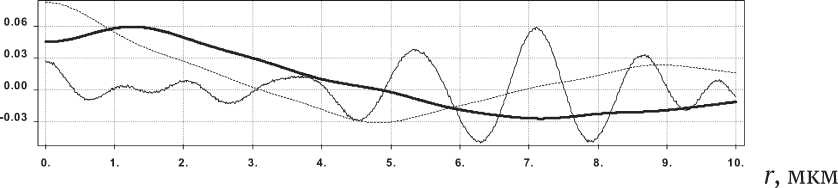
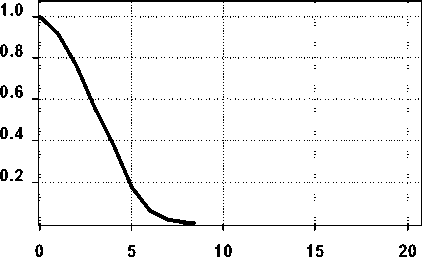
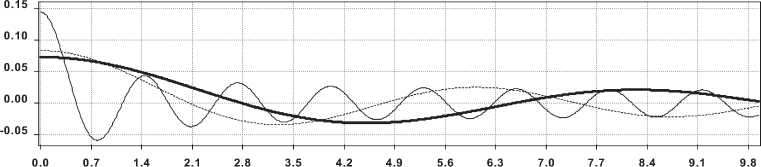
Рис. 4. График сечения действительной части нормированных собственных функций v n ( р ) ( n = 1 – толстая линия, n = 2 – пунктир, n = 15 – тонкая линия) для

(а) r₀ = 10 1 , z = 0.5 1 , а ₀ = 10, (б) r₀ = 10 1 , z = 20 1 , q ₀ = 1

3.    МОДЕЛИРОВАНИЕ РАСПРОСТРАНЕНИЯ РАССЧИТАННЫХ СОБСТВЕННЫХ ФУНКЦИЙ

Для моделирования распространения рассчитанных собственных функций в свободном пространстве использовалось выражение (3). Результаты моделирования показаны в Таблицах 1 и 2.

Как видно из результатов, приведенных в Таблице 1, поля, согласованные с собственными функциями, распространяются в свободном про -странстве с сохранением своей структуры . Для соб - ственных функций низкого порядка характерно более длительное сохранение структуры, чем для функций высокого порядка. В частности, при n=1,2 видно полное сохранение структуры на расстояние 5l, в то время как при n=15 на этом же расстоянии периферийная часть поля теряется. Заметим, что сформированные поля и их пространственные спектры похожи на моды Бесселя [56].

Как видно из результатов, приведенных в таблице 2, поля, совпадающие с «вырожденными» собственными функциями, распространя-

Таблица 1. Моделирование распространения собственных функций V n ( р , z ) рассчитанных при параметрах: r ₀ = 10 1 , z = 0.5 1 , а ₀ = 10 (распределения показаны в негативе)

Таблица 2. Результаты моделирования для полей, совпадающих с собственными функциями, рассчитанными для параметров r₀ = 10 Х , z = 20Х , о ₀ = 1 .

ются в свободном пространстве и сохраняют его структуры только в центральной части.

ЗАКЛЮЧЕНИЕ

В рамках данной работы для ограниченного оператора распространения в ближней зоне дифракции был выполнен расчет осесимметричных собственных функций. Показано, расстояние распространения и ограничения, наложенные в объектной и спектральной областях имеют значительное влияние на качественные и количественные характеристики собственных функций. Результаты моделирования показывают, что поля, совпадающие с рассчитанными собственными функциями, распространяются в свободном пространстве с сохранением его структуры. Для собственных функций более низкого порядка характернее более длительное время сохранения, чем для функций более высокого порядка.

Данное исследование финансировалось РФФИ в соответствии с исследовательским проектом № 18-37-00056.