Вычисление индекса Пуанкаре: описание "неколлинеарного случая" в пространствах произвольной конечной размерности

Рассмотрим задачу о вычислении индекса Пуанкаре нулевой изолированной особой точки (нуля) векторного поля в случае, когда производная Фреше в этой точке (линейная часть) – ненулевая вырожденная матрица.

В статье [1] нами описан векторный метод, в котором дается достаточное условие того, что искомый индекс плоского векторного поля определяется совокупностью линейной и квадратичной частей векторного поля, а члены более высоких порядков малости на индекс не влияют. Этот случай, названный нами неколлинеарным, предполагает, что в тех точках, где линейная часть обращается в ноль, векторы квадратичной части не коллинеарны ненулевым векторам линейной части, которые на всей плоскости направлены вдоль одной и той же прямой.

Рассмотрим обобщение векторного метода на произвольное конечномерное пространство для случая, когда матрица линейной части имеет ранг n-1, где n – размерность пространства.

Постановка задачи

Пусть векторное поле Ф2: Rn→Rn имеет вид

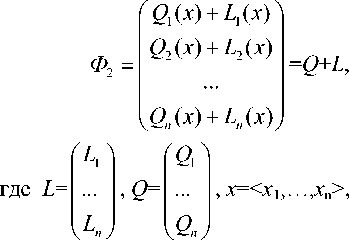
L i (x)= а л x 1 + a _i2 x ₂+_+ a _in x _n ( i = 1, n ), A =( a j ) -вещественная матрица линейной части векторного поля Ф 2 , Q – квадратичная часть векторного поля Ф 2 . Пусть далее матрица А имеет ранг n– 1.

Необходимо обобщить векторный метод на этот класс полей, указав для них аналог неколлинеарного случая.

Описание многомерного обобщения неколлинеарного случая

Если векторное поле вида (1) имеет линейную часть, причем ранг ее матрицы равен n -1, то пространство решений уравнения Lx = θ , т.е. ядро оператора L , имеет размерность, равную n -( n -1)=1. Аналогично плоскому случаю, это одномерное подпространство пересекает любую n -мерную сферу с центром в нуле в двух точках: x * и – x *.

Множество значений оператора L является линейным подпространством пространства Rⁿ и имеет размерность:

dim (Im ( L ))=dim( R ⁿ) - dim(Ker( L ))= n -1.

Аналогом неколлинеарного случая для плоских векторных полей будет случай, когда выполнено условие

Q ( x *) ? Im( L ). (2)

Заметим, что, поскольку Q является четным векторным полем, справедливо равенство Q (- x *)=Q( x *).

Можно показать, что если векторное поле содержит члены более высоких степе- ней, т.е. имеет вид

( W ( x ) + Q 1 ( x ) + L 1 ( x ) Л

Ф =

W ₂( x ) + Q ₂( x ) + L ₂( x )

= W + Q + L ,

I Wn (x) + Qn (x) + Ln (x) J где W(x) = o(||x||2) (i=1,n), матрица линейной части имеет ранг n-1 и выполняется условие (2), то индексы нулевых особых точек векторных полей Ф и Ф2 равны в силу их гомотопности на границе сфер малых радиусов.

Если отсутствует квадратичная часть ( Q = θ ), то аналогичные рассуждения можно проводить для однородной компоненты, которая следует непосредственно за линейной.

Пример. Рассмотрим векторное поле вида

^Л W ( x ) + Q j ( x ) + x

W ₂ ( x ) + Q ₂ ( x ) + x₂

Ф =

W n - 1^{( x} ) ^{+ Q} n - 1^{( x} ) ^{+ x} n - 1 . W n ( x ) + x n²

Имеем: Ker ( L )=(<0,…,0, C ); dim(Ker( L ))=1; Im( L )={< C 1 , …, C n-1 ,0>}.

Последняя компонента вектора Q (<0,0,…,1>) равна 1. Следовательно, Q (x*) ^ Im( L ), и от векторного поля Ф можно перейти к полю Ф ₂ без компоненты W .

Действительно, если обобщить лемму [2, с.72] на многомерный случай и применить ее к данным векторным полям, то получим, что индексы нулевых точек обоих полей Ф и Ф 2 равны нулю.

Замечание

В неколлинеарном случае для полей рассматриваемого класса нулевая точка всегда будет изолированной. Если линейная компонента L обращается в нуль, то отлична от нуля следующая за ней компонента, которая "перевешивает" все компоненты более высоких порядков малости. В противном случае наиболее весомой оказывается ненулевая линейная компонента.