Вычисление собственных чисел эллиптических дифференциальных операторов с помощью теории регуляризованных рядов

Т = -А =¹— sin y дУ

1 d ² )

■ о д Siny--- . . , дУ  sin2 У дф ,

действующий в гильбертовом пространстве Н. Собственные числа оператора Лапласа–Бельтрами образуют систему ортонормированных сферических функций. Обозначим Xn = n ( n + 1) ( n = 0, ~) - собственные числа, vn = 2n +1 - кратность собственного числа Xn опе ратора Т; vni (i = 0,2n) - собственные функции, ln = {X|X = An + n +1 + ip, -~< p <+^} - прямые на комплексной плоскости, цп i - собственные числа оператора T + P

|uni - n ( n + 1 )| < const.

Определим собственные числа дифференциального оператора с помощью теории регуляризованных рядов. Рассмотрим четырех поправки теории возмущений.

Первая поправка теории возмущений [1]

^n           2 m + 1

i = 1                 ^{4 n} F

2 n

Вторая поправка теории возмущений a n ( p ) к сумме У u ni представляется формулой [3]: i = 0

a n ( p ) =—L Sp J f- f    х Г ( T -X E ) 1 P ² 1 ( T -X E ) 1 d X > =

2ni      J J L                J in ln-1

n

l n - 1

^

^a k , n k =^y . n |^Xk ^{- X}n| ’

2k2n an, k = У У (Puki, unj) (Punj, uki). i=0 j=0

Кадченко С.И., Торшина О.А.

Вычислим вторую поправку теории возмущений. Для этого введем так называемое Л преобразование f ( а ) функции p ( 6 , ф ) [2]. Обозначим T ( а ) - пересечение конуса со сферой, ф ( 6 , 6' , а ) - якобиан перехода 6 . ф . 6 , ф к координатам 6 , ф , 6 , а .

ф ( 6 , 6 ', а ) = ±

sin а

( - cos а + cos ( 6 - 6' ) ) ( cos а - cos ( 6 + 6' ) )

При этом знак «плюс» берется, если ф <  ф , знак «минус», если ф >  ф . Тогда [4]

f ( а ) = JJ p ( 6 , ф ) sin 6 d 6 d ф JJ p ( 6 , ф ) sin 6' F                     T ( а )

ф ( 6 , 6 , а ) d 6 sin а

(2к +1)(2n +1)П , ак,n =----П-----* f(а)^Li (P2к (C0SаLi (P2n (^^))sin^^

Очевидно, что функция f ( а ) нечетная, то есть f ( а ) = - f ( п - а ), 0 <  а <  п . Докажем, что f (0) = f ( п ) = 0. Для этого введем функцию [6]

Z ( а ) = ^

( sin а ) ²,

/ ■ „ А -2      ^П

-(sin а) , у

П

Если f (0) = f ( п ) Ф 0, то J f ( а ) ^ ( а ) sin а d а   . С другой стороны [5]

П

J f ( а ) ^ ( а ) sin а d а

JJJJ

FF

p ( 6 , ф ) p ( 6 ' фр ) sin 6 sin 6И6 d 6'dф d ф

sin а

FF

= ^const JJJJ

FF

а О ф 6 ф ф ф ф sin а

< ^const JJJJ

FF

sin а

J ( - cos а + cos ( 6 - 6 ) )( cos а - cos ( 6 + 6 ) )

В результате, f (0) = f ( n ) = 0. Докажем, что функция f ( а ) почти всюду дважды дифференцируема и f ‘ ( а ) е L 1 [ 0, п ] . Запишем равенство [8]

FF d6dфd6 Ha.

J ( - cos a + cos ( 6 - 6 ) )( cos a - cos ( 6 + 6 ) )

Далее имеем [7]

FF d6dфd6da =

( - cos а + cos ( 6 - 6 ) )( cos а - cos ( 6 + 6 ) )

=± П 3d7 {p (6,ф) p (6 ,ф)}фе (а)sin 6 sin 6 х

FF

Математика

J ( - cos a + cos ( 9 - < 9 '))( cos a - cos ( 9 + 9 '))

FF

J( - cos a + cos ( 9 - 9 '))( cos a - cos ( 9 + 9 '))

± 1 ЛЛ p (^{9 ,} ф ) p ' ( ⁹ V )

2 FF

sin aq ( a )

32                   12

( - cos a + cos ( 9 - 9 ) ) ( cos a - cos ( 9 + 9 ) )

±¹ЛЛ p ^{( 9} , ^ ) p ⁽⁹' , ^ф ) 7----si ^f -^w r------TEE^sin ^{9 sin 9 d 9 d} ^ ^{d 9}' ^{d a}

² F F                ( - cos a + cos ( 9 - 9 ) ) ( cos a - cos ( 9 + 9 ) )

Произведем замены: в первом интеграле 9 - 9 = aсhф, 9 + 9 = aсhф', а во втором 9-9' = aсhф, 9 + 9' = ashфchф', в третьем интеграле 9-9' = aсhф, 9 + 9' = ashфchф'. В ре зультате по формуле Фубини получим f '(a)e L1 [0,п], где производная взята в смысле С. Л. Соболева [9].

Далее

0 FF х ------------;----sin^;----— q (a) q (a) sin 9 sin 9'd 9d фd 9 di a +

( - cos a + cos ( 9 - 9 ))( cos a - cos ( 9 + 9 )) ^v ’ ^v ’

± ¹ЛЛ p ( ^{9 ,} ф ) p ( ⁹ , ^ ) 2 _FF

sin aq ( a ) q ( a )                1

sin 9 sin 9' d 9 d ф d 9 d i a ±

( - cos a + cos ( 9 - 9 ') ) 32 ( cos a - cos ( 9 + 9 ') ) 12

² ff               ( - cos a + cos ( 9 - 9 ) ) 1 ² ( cos a - cos ( 9 + 9 ) ) 3 ²

По аналогии в формуле для f' ' ( a ) получим cos a                                         sin² a

( - cos a + cos ( 9 - 9 ') ) 12 ( cos a - cos ( 9 + 9 ') ) 32 ( - cos a + cos ( 9 - 9 ') ) 12 ( cos a - cos ( 9 + 9 ') ) ^5/2

Сделаем замены 9 + 9 ' = a ch- ф , 9 - 9 ' = a 4 sh ф сКф' , - 9 + 9 ' = 2 a сh ф , 9 - 9 ' = a ³sh³ ф ch ф' .

Воспользовавшись теоремой Фубини, получим, что f '' ( a ) е L 1 [ 0, п ] и существует почти всюду [11].

Вычислим [10]

2 n

L1 (P2n (cosa)) + L2 (P2n (cosa)) = Е m=0

. nm sin

n m cos

х

d 2 ₂ d 2 ₂

2 n 22 n 2 n 2

х П -^Нт-P2n ( cos a ) = Е П -^Нт-Pk ( cos a ) = k = 0, k ^ m ^{m - k}                 m = 1 k = 0, k ^ m ^{m - k}

2 n 2 n

= Е П m=1 k=0, k^m

d ² d/'

- k ²

22 m k

2 n

2Е s=0

⁽ n ^- s ^{) !} p( s )

5 s ( n + S ) ! ² n

( cos 9 ) P^ nS ) ( cos 9 ) cos s ( ф - ф' ) =

2 1 ( n - X ) !                                             2 n 2 n 2 - k ²

= ² Z L . X. P 2 n ( cos ⁹ ) P 2 n ( cos ⁹ ) cos ^{X Ф -} Ф^ Z П 2 ,2 = P 2 n ( ^{cos a} ) .

X = 0 3_S ( n + ^X ) ^!                                        m = 1 _k / // m m 2 - к 2

Тогда

(2 к + 1)( 2 П + 1) П , x2^ z ak,n =----n-----J f (“) Z Li (P2k (cos")) ZL (P" (cos^)sin“d" =

( 2 k + 1 )( 2 n + 1 ) П , _x ,

= 2----- -I f ( a ) P _{2 k} ( cos a ) P _{2 n} ( cos a ) sin a d a .

^{4 n}      0

В результате вторая поправка теории возмущений an ( P ) = -

( 2 n + 1 ) 4 n ²

^

z k=1, k # n

2 k + 1 ⁿ I ^ k - ^ n\ ^J

a ) P _{2 k} ( cos a ) P_2n ( cos a ) sin a d a =

4 n ^г

^

z k=1, k ^ n

2 k + 1

I л - Л .1

E П J + J . 0 n-E

f ( a ) P _{2 k} ( cos a ) P _{2 n} ( cos a ) sin a d a +

n-E

+ I f ( a ) P _{2 k} ( cos a ) P _{2 n} ( cos a ) sin a d a > .

E

Воспользовавшись [5]

^P2k ( ^{cos a} ) =

cos { ( 2 k + 12 ) a - П 4 }

( 2 пТ ₊ о (1) 2 k ¹² 2 k ³²

( sin a )

sin { ( 2 k + 3/2 ) a - nJ 4 } о (1)         о (1)

( sin a ) 3 2          ² k 3 ²    ( sin a ) 5 2 2 k 5^2

Получим:

^a n ( P ) = ^-

2 т + 1 4 n ²

^

z k=1, k ^ n

2 k + 1

PA

J + J

_L о n -.

f ( a ) sin a P_2k ( cos a ) P _{2 n} ( cos a ) d a +

п-E

+ J

E

_{z 4 z} J cos { ( 2 k + 1 ) a - n /4 } ^{f ( a ) sin ( a )}(------ —-12-----

\       ( sin a )

( 2 nf . O ( 1 )

(2/ k ) ^V 2 (2/ k ) ^3/2

+

sin { ( 2 k + 3/2 ) a - П 4 } O (1)          O (1)      \/cos { ( 2 k + 12 ) a - П 4 } ( 2/ n ) 1 ²     O ( 1 )

( sin a ) ³²         ( 2 k ) 3 ²    ( sin a ) 5 ² ( 2 k ) 52           ( sin a ) ¹²          ( 2/ k ) ¹²    ( 2/ k ) 3 ²

sin { ( 2 k + 3/2 ) a - nJ 4 } O (1)           O (1)

( sin a ) ³²         ( 2 k ) 3 ²    ( sin a ) 5 ² ( 2 k ) 5^ ²

где E - положительное число f (a ) = JJ p (9, ф) sin 9d9dф

F

П p ( 9 , ф) sin 9- ^⁹- ⁹ - ^a ) d ⁹ sin a

F

С учетом асимптотических формул [4] получим

, X 2, \  ^( Elnn / „/ E / „( E / ^( E ln n / „/E ln n / an (p) = O ( e ln n) + OI-----I + OI —тут-1 + OI — I + OI —т— I + OI —т— I + v к n /    к n3/2 7 I n J < n2 7 I n2 7

+ O I ^E 2 1+ O I ^E^ к n ² 7 к n

n-E

1 f X . ( I E In n ) , —— f ( a ) ctg ( n - a ) d a + O I——I + 4 n ² n E к n ² 7

I In n / Д In E In n / Д In n / Д In n / Д 1 I ^f 1

+OI     I+ OI I+ OI — I+ + OI I+ OI I+ OI — к n3/2 7     к n3/2 7     кn3E7      кn3/2 7     кEn3/2 7     к n3E^

.

Математика

Выбирая в качестве e = ^4 , найдем n

1 П-E                                С ] \ a (p)=v^ J f(a) ctg (n - a)da+0l^I.

4 n ² n E                       V n )

Учитывая, что j f ( a ) ctg ( n - a ) d a = 0, получим

E

₍ x _ f In n ) ^a n ( P ) = O l ^72 I .

Вычислим третью поправку теории возмущений

P n ( p ) = Sp f-f   Г P ( T - X E ¹ 1 3 d X = 1-Sp        X

( 2 n + 1 )( 2 k + 1 )( 2 1 + 1 )

~        ~         ~ "       c d X X

( X n - X )( X k - X )( X - X )

6ni    ; у L J        6ni     • ^j

_ ln ln-1 J                                                      L ln ln-1 - f 1

X l T I jjjjjj P (9,ф)P (0 ф P (0 ф ) Pn (cosa) Pn (cos e) Pn (cos У )X

^{V 4 П )} F F F

X sin в sin 0 sin 0"d ф dф'd ф d 0 'd 0 , cos a = cos 0 cos 0 + sin 0 sin 0 cos ( ф - ф ) , cos в = cos 0 cos 0' + sin 0 sin 0 cos ( ф - ф ' ) , cos у = cos 0 cos 0 + sin 0 sin 0 ' cos ( ф - ф ') . Если в шестикратном интеграле сделать замену ф ^ П + ф , 0 ^ П - 0 , то

P n ( cos ( п - a ) ) = P n ( - cos a ) = ( - 1 ) n P_n ( cos a ) , P l ( cos ( п - у ) ) = P l ( - cos у ) = ( - 1 ) l P l ( cos у ) .

В результате

P n ( P ) = 0.

Для оценки четвертой поправки докажем теорему.

Теорема 1. Для оператора Лапласа–Бельтрами с дважды непрерывно дифференцируемым потенциалом на l_n = { X | X = X _n + n + 1 + iP , - ^ <  p <  m } справедливо равенство

I( T - X E ) ^{- 1} Г < 1 0 (1)-,

I                   12    |e| + n где Xe ln и e = Im(X)

Доказательство. Имеем

(T -XE )-1 = X .. . k ,,22

² k = 0 ( X k - X n - n - 1 ) + e

n-1           vv у Vk+ vk k=0 (Xk - Xn - n -1) + e2 (n +1) + e2

m

+ ---------- ^k ----5-----= A\ + A 2 + A 3.

k = n + 1 ( X k - X _n - n - 1 ) + e

Оценим каждое из слагаемых в отдельности n-1

A1 = X k=0

vk

(Xk - Xn - n - 1) + e2

n - 1

= const j

( 2 k + 1 ) dk

( k ( k + 1 ) - n ( n + 1 ) - n - 1 ) ² + ee '

n - 1

= const j

( 2 k + 1 ) dk

( ( n + 1 ) - k ( k + 1 ) ) + e

Кадченко С.И., Торшина О.А.	Вычисление собственных чисел эллиптических дифференциальных операторов с помощью теории регуляризованных рядов
Оценим	n ( n "        dm           O (1) = const ------------ 5 ----< —--- . 0 ( ( n + 1 ) 2 — m ) + e 2    e + n A =      vt     = 2 n + 1 <  O (1) n = O (1) 2 ( n + 1 ) 2 + e 2 ( n + 1 ) 2 + e 2 ( n + e | ) 2 e + n

Здесь была использована эквивалентность норм | а | + | b | и ^| а |² + | b |² .

Далее

J

A 3 = E k = n + 1

vk

( ^ k - ^Л - n - ^{1 ) 2 +} e ²

= E k=n+1

2 к + 1

( n + 1 ) — к ( к + 1) I + e

Оценивая A ₃ аналогично A ₁ , получим

A 3 <

O (1) | e | + n

Теорема доказана.

Учитывая результаты теоремы 1, рассмотрим четвертую поправку теории возмущений.

—

п5pf — f (P (T — AE)-1 )* dA < ln ln—1

n

l n — 1

w

< O (1) f ( T — A E )

— 1

j

( T — A E ) ¹

² d A <  O (1) J — d ^ -y 1(1 ^ + n ) 3

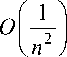
Теорема 2 . Пусть p – потенциал, удовлетворяющий условию Липшица, тогда для собственных чисел оператора T + P верна оценка

1 ^П                           „Г In n ^

E ^ni — n ( n + 1)( 2 n + ')+ , 2 I f (a) ctg«(n — a) da = OH/ll .

i = 0 ,                         4 n ² n ^                                I n ^3/2 )

Интерес к подобного рода задачам все время возрастает в связи с широкой областью их применения [12–14].