Вычислительная процедура нахождения предельных значений параметров нагружения механических систем

Процесс деформирования материала в результате повреждения микродефектами может привести (и, как правило, приводит) к зависимости между напряжениями и деформациями, соответствующей разупрочнению, при котором напряжения падают, а деформации (закритические) растут. При этом не выполняется постулат устойчивости Друккера, и разупрочненный материал является реологически неустойчивым. С континуальной точки зрения этот эффект характеризуется падающей ветвью полной диаграммы деформирования, построенной для жесткого одноосного растяжения [1, 2].

При учете стадии разупрочнения материала возникают две проблемы. Первая заключается в усовершенствовании моделей материала с целью описания его деформирования на закритической стадии и построении соответствующих определяющих соотношений для неодномерного нагружения. Вторая связана с разработкой математических методов анализа устойчивости процесса деформирования (потеря устойчивости может быть интерпретирована как разрушение [3]). Потеря устойчивости ассоциируется при этом с переходом части материала в деформируемом твердом теле или части элементов конструкций механической системы на стадию неустойчивого деформирования (разупрочнения). В связи с этим возникает необходимость в установлении единственности решения краевых задач определения напряженно-деформированного состояния твердых тел и записи уравнений равновесия

механической системы с разупрочняющимися элементами, а также в создании численных методов и эффективных итерационных процедур решения нелинейных задач такого рода.

Устранение первой проблемы требует разработки специальных экспериментальных и теоретических методов для адекватного описания свойств материалов на закритической стадии деформирования. Для решения второй проблемы и апробации соответствующих математических методов и численных процедур необязательно иметь в распоряжении определяющие соотношения для реальных материалов. Допускается использование гипотетических моделей, которые на качественном уровне отражают основные свойства разупрочняющегося материала.

Полная диаграмма деформирования получается дифференцированием одномерной потенциальной функции, имеющей область выпуклости вниз (отвечает устойчивому состоянию материала), точку перегиба (пограничное состояние) и область выпуклости вверх (неустойчивость материала). Таким образом, с достаточной степенью точности можно считать, что при неодноосном деформировании с разупрочнением свойства материала описываются многомерной потенциальной функцией, имеющей область выпуклости вниз и, в общем случае, седловые точки (или области выпуклости вверх), а также точки, разделяющие состояния упрочнения и разупрочнения. Некоторые такие потенциальные функции, описывающие (не претендуя на общность) качественные характеристики разупрочняющегося материала, приведены в работе [4].

В данной работе рассматривается один класс градиентных дискретных механических систем, к которому относятся, например, стержневые системы. В подобных системах положение элементов определяется конечным числом обобщенных координат (обобщенных перемещений). Частично эти координаты могут быть задаваемыми величинами (жесткое нагружение) и представлять собой параметры управления, а остальные тогда играют роль параметров состояния. Также в качестве параметров управления могут выступать действующие на систему обобщенные силы (мягкое нагружение). В этом случае все обобщенные перемещения есть параметры состояния. Может иметь место и смешанное нагружение, когда задаются как силы, так и перемещения.

Поведение градиентной механической системы характеризуется ее потенциальной функцией W ( q i , Q j ) ( i = 1,..., N ; j = 1, ..., M ), зависящей от параметров состояния q i системы и параметров управления Q_j [5]. Предполагается, что часть элементов системы при ее монотонном деформировании может перейти на стадию разупрочнения, и, следовательно, тогда свойства этих элементов описываются невыпуклыми неодномерными потенциальными функциями, имеющими области выпуклости вниз и седловые точки. Поэтому данные механические системы могут потерять устойчивость (разрушиться) в процессе деформирования.

Для определения напряженного состояния элементов такой механической системы в положениях равновесия необходимо выявить все критические точки функции W из решений системы нелинейных уравнений V N W = 0. Здесь V N — оператор Гамильтона в евклидовом пространстве состояний R^N . В силу того, что некоторые потенциальные функции элементов системы являются невыпуклыми, данные уравнения могут иметь одно или несколько решений, или вообще не иметь решения. Особое значение приобретают вырожденные критические точки, в которых матрица устойчивости H ( W ) = V _N V _NW вырождена. Здесь H ( W ) — матрица Гессе вторых производных функции W [6]. Такие точки структурно неустойчивы [5]. Возмущение потенциальной функции W вызывает качественные изменения в поведении самой функции. Вырожденная критическая точка расщепляется на несколько изолированных (невырожденных) критических точек. Механическая система при этом скачком переходит в новое состояние равновесия.

Вырожденные критические точки образуют в евклидовом пространстве управлений R ^M -многообразия, являющиеся сепаратрисой функции W . Вне области, ограниченной сепаратрисой, механическая система обладает лишь одним положением равновесия или положений равновесия не существует совсем. Внутри данной области имеется несколько положений равновесия [5]. Известно [5, 7], что при выходе пути нагружения за пределы области, ограниченной сепаратрисой, положение равновесия механической системы становится неустойчивым, и она скачком переходит в новое устойчивое положение равновесия (если оно существует). В таком случае можно считать, что механическая система разрушается. Следовательно, предельные значения параметров управления определяет сепаратриса потенциальной функции механической системы. Ниже излагается численный метод построения сепаратрисы для градиентной дискретной механической системы.

Апробация изложенной методики осуществляется построением сепаратрисы и вычислением предельных значений параметров нагружения для стержневой механической системы, реализующей процесс трехосного растяжения элементарного куба из нелинейного материала, обладающего эффектом деформационного разупрочнения при его активном деформировании. При вычислениях свойства материала куба полагаются идентичными свойствам гипотетического разупрочняющегося материала, потенциальная функция которого приведена в работе [4].

• 2.    Методика численного построения сепаратрисы

• 3.    Механическая система, реализующая трехосное растяжение элементарного куба

Для построения сепаратрисы необходимо сначала найти все критические точки потенциальной функции системы при возрастающих параметрах управления (нагрузках), а затем выделить из них вырожденные критические точки. Реализация данной схемы требует решения большого числа нелинейных уравнений для нахождения всех положений равновесия механической системы при квазистатическом возрастании нагрузок. Затем строится сепаратриса и определяются предельные значения параметров управления.

Возможен и другой подход к построению сепаратрисы. Он позволяет избежать решения систем нелинейных уравнений и заключается в следующем. Сначала дискретизируем с некоторым малым шагом евклидово пространство R N х R M внутри достаточно большого ( N + M )-мерного куба. В узлах сетки находим значения параметров состояния и управления. Подставляя эти значения в функции, составляющие элементы матрицы Гессе, получаем множество числовых матриц. Вычисляем детерминанты этих матриц и выделяем множество узлов L с их координатами в R N х R M , где гессиан близок к нулю с наперед заданной точностью. Очевидно, что множество L в общем случае содержит большее число элементов, чем множество вырожденных критических точек потенциальной функции W .

Подставляя координаты узлов из L в уравнения равновесия, выделяем те из них, которые с заданной точностью удовлетворяют этим уравнениям. Такие узлы и образуют множество вырожденных критических точек. Используя теперь параметры управления, отвечающие узлам с вырожденными критическими точками, находим в пространстве управлений вид сепаратрисы, по которой уже и определяем предельные значения параметров управления.

Будем рассматривать такие механические системы, для которых элементы матрицы Гессе есть функции только параметров состояния. В качестве примера исследуем процесс трехосного растяжения элементарного куба в специальной стержневой системе. Кубический элемент (Рис. 1) подвергается трехосному растяжению в системе, в которой растягивающие усилия на куб передаются через стержни 1, 2, 3, выполненные из линейно упругого материала. В недеформированном состоянии (отсчетная конфигурация) длина ребер куба равна единице. Грани куба с одной стороны скреплены шарнирами с абсолютно жесткими стенками, с другой — с упругими стержнями 1, 2, 3 таким образом, чтобы в процессе трехосного растяжения куб мог принимать форму только прямоугольного параллелепипеда. Точкам свободных концов стержней либо сообщаются монотонно возрастающие перемещения u1,u2,u3 (мм) (жесткое нагружение), либо к ним прикладываются монотонно возрастающие усилия P1,P2,P3 (кг) (мягкое нагружение).

Жесткости упругих стержней при растяжении соответственно равны Х 1 , Х ₂, Х ₃. Нагружение системы происходит при постоянной температуре и настолько медленно, что можно пренебречь динамическими эффектами.

В ходе нагружения грани куба в отсчетной конфигурации получают удлинения £ i ( i = 1, 2, 3). Грани нагружены равномерно распределенными усилиями q_i . Равнодействующие этих усилий равны с i = q i S ia , где S_ia — площади граней в актуальной (текущей) конфигурации. Величины с i имеют смысл номинальных напряжений, определяемых по элементарной теории. Величины £ i можно трактовать как деформации,

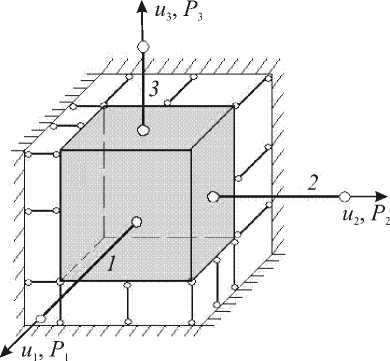
Рис. 1. Механическая система также определяемые в соответствии с

элементарной теорией.

Далее положим, что работа сил на перемещениях не зависит от вида траектории, по которой движется точка с координатами (£1, £2, £3) в евклидовом пространстве состояний Re3 , то есть движение точки, изображающей процесс растяжения куба, происходит в потенциальном силовом поле с некоторым потенциалом П(£1, £2, £3).

В качестве потенциала возьмем функцию вида [4]

П = B < 1 - exp

-

v E              2 E

—------— ( £ + £0 +£о ) + -

V

J2J

где B = const — величина потенциала в момент разрушения; E = 2 - 10 5 МПа — модуль Юнга; v = 0,3 — коэффициент Пуассона. Линии уровня потенциала П в пространстве деформаций R_e ³ представляют собой эллипсоиды. Для определенности зададим В = 10МПа . Тогда предельный эллипсоид, точки которого отвечают разрушению, имеет большую полуось b = 0,022 и малые полуоси a = 0,012.

В точках пространства R ^, где матрица Гессе H ( П ) положительно определена, потенциал П есть функция, локально выпуклая вниз [6], что отвечает физической (собственной) устойчивости материала куба (упрочнению). Область положительной определенности матрицы H ( П ) , включающая в себя начало координат, ограничивает множество меры нуль (поверхность в пространстве R 3 ), где матрица H ( П ) вырождена. В точках, расположенных за этой поверхностью, матрица H ( П ) знаконеопределена (ее собственные значения имеют разные знаки), что отвечает разупрочнению материала

(собственной неустойчивости). Таким образом, потенциальная функция П описывает свойства материала куба на всех стадиях его деформирования, а именно на стадии устойчивого деформирования (упрочнения) и стадии неустойчивого деформирования (разупрочнения).

• 4.    Сепаратриса и предельные значения параметров управления при жестком нагружении

При активном деформировании описанная выше механическая система градиентна и в случае жесткого нагружения описывается потенциальной функцией

W1 =ЕМ ui-l ^/2 + П(£1, £2, £3 )и ,                                          (1)

i = 1

где l = 1 мм — длина ребра куба; и = 1 мм3 — объем куба. Первые три слагаемые — это энергия деформаций линейно упругих стержней 1, 2, 3, в выражениях которых для определенности полагаем Xi = 5000МПа х мм . Наконец, в формуле (1) величины l£i есть параметры состояния системы, а ui — параметры управления.

Критические точки потенциальной функции W1 являются решениями системы уравнений W1i = (и/1)П -Xi (ui -1£i) = 0 (i = 1,2,3). Запятой обозначены частные производные по соответствующим параметрам состояния lsi. Отметим, что рассматриваемая механическая система относится к такому классу систем, уравнения равновесия которых могут быть разрешены относительно параметров управления. В данном случае

U. =—П . +1£

¹ l X_i ’ i         i

Компоненты матрицы Гессе являются тогда функциями только параметров состояния:

H (W1 ) = u l

IV»*^ П,2

^П ,21         ^X 2 /^{и + П} ,22

№    П ,32

ПД3         1

П ,23

Х3/и + П,зз

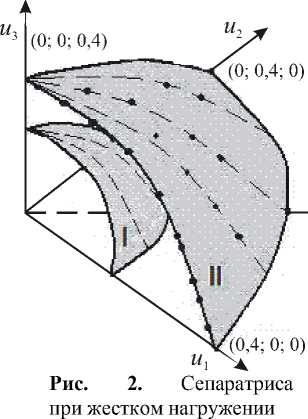
При монотонном возрастании параметров u параметры состояния удовлетворяют соотношению £ i > 0. Выделим на множестве D = { £ i ^ 0 } куб 0 <£ i <  0,0086 и построим в нем объемную сетку с шагом 4,5 • 10 - ⁴. В каждом узле сетки вычислим значение det H ( W 1 ) и выделим те узлы, в которых детерминант близок к нулю. Координаты этих узлов подставим в уравнения (2) и найдем значения u_i^s — координаты точек сепаратрисы. Натянув на точки ( u ₁ ^s , u ₂ ^s , u ₃ ^s ) поверхность, получим

приближенный вид сепаратрисы (Рис. 2).

Сепаратриса состоит из двух поверхностей: I и II. Предельные значения параметров управления определяют точки поверхности II. При последующем нагружении в пространстве управлений значения параметров пересекают поверхность II, происходит катастрофа (внезапная потеря устойчивости процесса деформирования механической системы). Координаты точек, лежащих на сепаратрисе и определяющих предельные значения параметров управления, можно представить в виде таблицы (Табл. 1).

Таблица 1. Координаты некоторых точек, расположенных на сепаратрисе при жестком нагружении

Параметры управления (перемещения)	Координаты (предельные значения), мм
u 1 s	0,314	0,342	0,361	0,382	0,310	0,209	0,289	0,242
u 2 s	0,357	0,299	0,202	0,220	0,266	0,353	0,198	0,227
u 3 s	0,180	0,227	0,260	0,310	0,339	0,353	0,386	0,400

5. Сепаратриса и предельные значения нагрузок при мягком нагружении

Потенциальная функция при мягком нагружении системы имеет вид ₃ u_i

W 2 = W 1 - ^ J Pde _t , где три последних слагаемых — это работа растягивающих усилий, = 1 0

взятая со знаком минус. Теперь параметры состояния — это 1 s , , и , а параметры управления — растягивающие усилия P_i . Критические точки функции W ₂ являются решениями системы уравнений

W^W 1 )n ,-X, (и,-1 s,) = 0,   W^-X, (u-1s,)-P = 0.                  (3)

3 X                        3 u i - ^{1 s}

Представим функцию W ₂ следующей суммой: W ₂ = V^ + У — ( u- - 1 s )² -X J Pde , где 1=1 2^         t? о

• 3 ^{1 s} ,

• V 2 = un ( s 1 , s ₂, s ₃ ) - ^J Pdei . Здесь функция V 2 — потенциальная функция такой = 1 0

механической системы, в которой отсутствуют линейно упругие стержни, а нагружение куба осуществляется силовым способом. Таким образом исключаются параметры u и X _i . Критические точки функции V ₂ определим из решения уравнений

vu=(U 1 )п,-P = 0 (р = п,).

Отметим, что уравнения (4) — это вторая группа уравнений (3), в которых выражения

X , . ( и - 1 sj заменены на (и/ 1 ) П _s

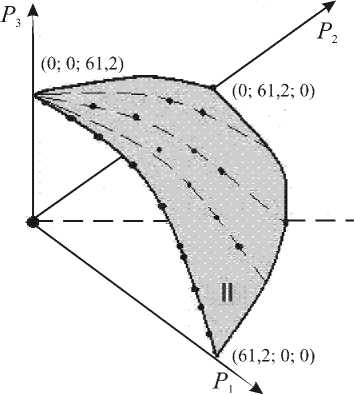
Рис. 3. Сепаратриса при мягком нагружении

в силу записи уравнений первой группы.

Сравнивая системы (3) и (4), находим, что они имеют одинаковое число решений, которое зависит только от значений управляющих параметров P , причем в положениях равновесия основной и упрощенной механических систем величины P определяют одни и те же параметры состояния. А это означает, что критические точки функции V ₂ есть проекции критических точек функции W ₂ в пространство меньшей размерности: ( s , , u , , р ) ^ ( s , , р ) . Тогда и проекции вырожденных точек функций W ₂ и V ₂ в пространство управлений совпадают и определяют одну и ту же сепаратрису. Таким образом, параметры и , и X , несущественны для анализа устойчивости процесса мягкого нагружения данной механической системы.

Найдем сепаратрису функции V ₂ в пространстве управлений P_i . Имеем

1Э Г^П ,11 ^П ,12 ^П 13 HV ) =Т П ,21 П ,22 П ,23

l П з П з J

На том же кубе в пространстве Re3 с той же сеткой узлов вычислим в каждом узле det H (V2) и выделим те узлы, в которых детерминант близок к нулю с достаточной степенью точности. Координаты этих узлов подставим в уравнение (4) и найдем значения Pis — координаты точек, лежащих на сепаратрисе. Натянув на точки P1s ,P2s,P3s поверхность, получим приближенный вид сепаратрисы (Рис. 3). Она состоит из точки — начала координат, и поверхности II. Если путь нагружения пересекает эту поверхность, то происходит катастрофа. Координаты точек, лежащих на сепаратрисе и определяющих предельные значения нагрузок, можно представить в виде таблицы (Табл. 2).

Таблица 2. Координаты некоторых точек, расположенных на сепаратрисе при мягком нагружении

Параметры управления (предельные нагрузки)	Координаты (предельные значения), Н
P 1 s	1638	1551	1341	2058	1324	1533	1253
P 2 s	1498	1760	1570	1009	1394	1882	2162
P 3 s	939	992	992	1009	905	1114	1114

• 6.    Заключение

Для определения предельных нагрузок, действующих на дискретные градиентные механические системы, приведена методика их численного расчета, позволяющая избежать решения большого числа нелинейных уравнений равновесия. На примере одной стержневой системы, реализующей трехосное растяжение куба, по изложенной методике проведены расчеты предельных параметров управления при жестком и мягком нагружениях.

Работа выполнена при финансовой поддержке РФФИ (проекты № 10-08-00135, 10-01-96018_Урал).