Вычислительно эффективное решение по нахождению плотности тока на освещенной и теневой сторонах бесконечно тонкого круглого диска

Одной из канонических задач теории дифракции в векторном (электромагнитном) случае является задача дифракции на бесконечно тонком идеально проводящем круглом диске [1]. Ее исследованию в отношении внешней и внутренней задач электродинамики для стороннего плоского монохроматического поля произвольной поляризации и произвольного направления падения посвящено большое число работ [2–10] и др. Их основу составляют следующие решения: 1) аналитические, формируемые при применении метода разделения переменных и представления волновых уравнений в вырожденной эллиптической системе координат с получением решения в виде ряда по сфероидальным функциям [2; 3]; 2) асимптотические, реализуемые в приближениях физической оптики [4], физической теории дифракции [5], геометрической теории дифракции и ее модификаций [6; 7]; 3) численные, основанные на применении метода моментов [8] или его модификаций [9; 10].

Указанные решения в исследовании дифракционной задачи на бесконечно тонком идеально проводящем круглом диске при применении метода конформных отображений [11; 12] потенциально позволяют обобщить получаемый результат на более сложные геометрические структуры [13–15]. Вместе с тем перечисленные методы в существующих реализациях не позволяют вычислительно эффективно выделить поверхностную плотность тока на освещенной и теневой сторонах круглого диска.

Цель настоящей статьи состоит в устранении указанного недостатка путем формирования вычислительно эффективного алгоритмического решения, основанного на методе моментов и позволяющего численно определять гладкую аппроксимацию поверхностной плотности тока на освещенной и теневой сторонах бесконечно тонкого идеально проводящего круглого диска.

1. Постановка и решение задачи дифракции

Пусть Q с К ² = ( x з = 0) с К ³ - бесконечно тонкий идеально проводящий диск радиусом R с

центром в начале координат и границей 5Q = = Q \ Q , а E 0 , H 0 - падающее стороннее плоское монохроматическое поле (рис. 1).

Задачу дифракции E 0 , H 0 на Q сведем к определению рассеянного электромагнитного поля (ЭМП) [16]:

E, H е С2 (К3 \ Q) х х Qc[ ®+ \5Q5 Ю С[ К3 \ 5Q5 |, 5>0 х          ^8>0 х^

удовлетворяющего условиям [1; 13]:

Vx H = -ipE, Vx E = ipH, x е К3 \ Q;(2)

^etL =- ^{e 0}|_q ; ^E 0 I^{е с} ” ^{( Q )}; E^H е L 2oc ^{( К} 3 );

E , H = o ( r ~1 ), r : = |x| ^» , Im P> 0;

H x e r - E = o ( r ¹); E x e r + H = o ( r ¹);

E, H = O(r 1), r ^® при Im P = 0, где x = { x 1, x 2, x 3};    er = x I |x|;

P 2 = й ² ц ( £ + i его ^{- 1});

го >  0 - угловая частота; s >  0 и ц >  0 - абсолютные диэлектрическая и магнитная проницаемости среды; индекс т обозначает тангенциальную составляющую поля на Q ,

5Q g = { x : |x - y| <5 , y е 3Q } .

Доказательство существования и единственности решения задачи (1)-(2) при Im Р> 0 известно из [16, с. 45]. Используя векторные потенциалы и граничное условие для ET из (2), представим (1)-(2) в виде gj = -f,                                                (3)

где

G J = V^ ( V- J ) + P ² ^ J ; f = i ro ( s + i его ^{- 1}) E 0 ;

tIq

^ J ( x ) = j G ( x , y ) J ( y ) d y ; x = { x ₁ , x ₂ , x 3 } e Q ;

Q

_{1 e} ^j P|^{x -}y|

J ( y ) - n = 0; G ( x , y ) =

4 P x - y|

• - функция Грина; J ( y ) = J e ( y ) + J h ( y ) - поверхностная плотность тока на Q , представленная суммой безвихревых J e ( y ) и вихревых J h ( y ) токов [17]; n = (0,0,1) - орт нормали к Q .

Решение задачи (3) выполним в проекционной постановке метода Галеркина [18] при разложении:

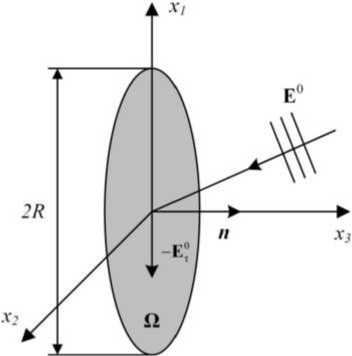
Рис. 1. Геометрическое представление задачи дифракции плоской волны на бесконечно тонком идеально проводящем круглом диске

Fig. 1. Geometric representation of the problem of diffraction of a plane wave on an infinitely thin perfectly conducting circular disk

M

J ( x ) = ^ C j V j ( x ),                                      (4)

j = 1

искомой функции J по базису V j ( x ).

С учетом первой формулы Грина [1] и свойств дифференциальных операторов [19] при удовлетворении Vj граничным условиям уj ’v| = 0, (v - нормаль к 5Q) выражение (3) при требовании ортогональности j Я (x)у j (x)d x = 0

Q невязки

M

Я ( x ) = G ^ C j у j ( x ) - f ( x )

к у j ( x ) примет вид

M Гг

^ C j - j V у _j ( x ) - j G ( x , y ) V у j ( y ) d y d:

: x -

_ Q Q

j = 1

- P ² j у _i ( x ) - j G ( x , y ) у j ( y ) d y d x Q Q

= j f ( x ) - у _j ( x ) d x .

Q

Эффективность решения (5) существенным образом зависит от выбора у j для Q . При этом исследование задачи предлагается формировать из функций у j , способных в последующем численном решении (5) и аппроксимации (4) обеспечить возможность представить J ( x ) в виде суммы безвихревых J e ( x ) и вихревых J h ( x ) токов.

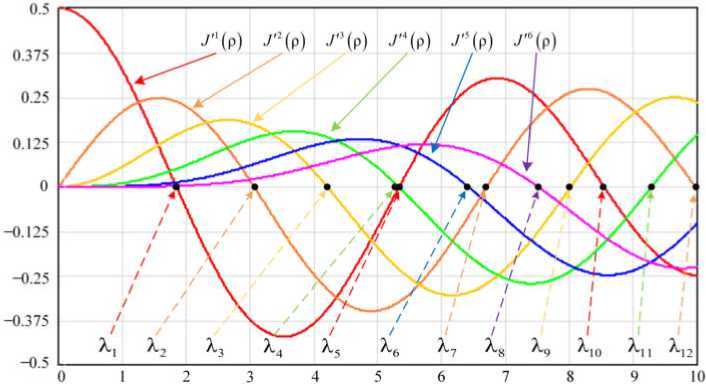
Рис. 2. Примеры графиков J '“ ( р ) и расположение первых 12 элементов множества нулей X = { X “ ( к )}

Fig. 2. Examples of graphs of J '“ ( р ) and location of the first 12 elements of the set of zeros X = { X “ ( к )}

• 2.    Решение дифракционной задачи с учетом разделения поверхностной плотности тока на вихревую и безвихревую составляющие

Особенность предложенного решения состоит в формировании гладкой аппроксимации J ( x ):

^*           ^*             ^*

J(x) = Je (x) + Jh (x), заданной конечными суммами: ",

NN

^{J (} x ) = ^ cj- ^ j ^{( x )} + 2 c h ' V h ^{( x )},

Тогда с учетом граничных условий на dQ решение задачи (5) на Q определим:

"

NN

J ( x ) = 2 c e ■ V₁ Ф N ( x ) + 2 c h ■ ^Ф D ( x ).

j = 1                     j = 1

В качестве ф N и ф D предлагается применять двумерные модифицированные функции Бесселя первого рода действительного переменного J j ( x ) и многочлены Цернике Z j ( x ), удовлетворяющие условиям (6) и (7) соответственно.

Удовлетворяющие граничному условию Неймана (6) функции Jj (x) зададим в виде где N, N - количество базисных функций каждого типа.

Согласно [20], для x eQ имеет место двумерный аналог декомпозиции Гельмгольца, который для поля H имеет вид

H = V1■ф D + V^-фN, где

^"              ^"

J j ( x ) = J j ( р , ф ) =

J ^а ( X “- _{+ 1} )/ ₂ p )^cos( к ф ), j mod2 = 1,

J ^а ( X ^a <2 p )sin( к ф ), j mod2 = 0,

где

р = р ( x ) = xx + + x 2 ; p< 1;

^V ± =

д д

ф = ф ( x ) = arg( x 1 + ix 2 );

V I =

д x 1 d x 2 I

д д

—

d x 2 ’ d X i J ’

J ^а ( р ) - функции Бесселя перового рода порядка а >  1; X = { X а ( к )} - упорядоченное по возрастанию X i < X i ₊ 1 (рис. 2) множество всех нулей

ф ^N , ф D - неизвестные скалярные функции, удовлетворяющие условиям Неймана:

dJ а ( р )
d р	а p=X i

= 0; X i ^ 0;

V1ф■ N -v   = 0, х 5Q и Дирихле:

Ф DI = 0, 5Q соответственно.

k – порядковый номер нуля функции

dJ ^а ( р )

J '^а ( p ) =           ;

d р

i e|_ 1, N / 2 J - порядковый номер элемента множества X .

Модификацию Zj(x) функций Цернике Zj(x) при удовлетворении граничному условию (7) опре делим как

Z j ( x ) = Z m (pY R m ^(PY ^m Y >  ^0;

^ R m ( p )sin ( — m p ) , m <  0,

R m ( p ) =p (i —p 2 ) p n — m Yp²

—

1),

где

P t ^(a>P)( x ) =

r ( a + 1 + 1) ----------------X t ! Г ( а + в + 1 + 1)

— в ² j v e ( x ) j G ( x , y ) v j ( y ) d y d x > =

Q Q                  ^[

= j f ( x ) v ej ( x ) d x .

Q

Решение системы уравнений (11), (12) позволит определить поверхностную плотность тока J ( x ) с требуемой точностью при обеспечении возможности выделения тока на освещенной J ^0CB( x ) и теневой J ^TeH( x ) сторонах диска.

X

* f t Vr( a + ₽ + 1 + s + 1)Y x — 1 f

s = 0 v ;

Г ( а + s + 1)

- многочлены Якоби порядка t ; n e N ; m e Z /{0}; n > | m |;

n — m

-----e Z ;

j = 0,5( n ² — 1 — n mod 2 + sgn( m )) + | m |.

Примеры графического представления предложенной модификации функции Бесселя первого рода действительного переменного J j ( x ) и многочленов Цернике Z j ( x ), удовлетворяющие условиям (6) и (7) соответственно, приведены на рис. 3.

С учетом поставленной задачи дифракции и предложении аппроксимации поверхностной плотности тока в виде (8) зададим (5) виде системы уравнений:

N [f,,

Xcj. -^ Jv-vj (x) J G( x, y )V-vj. (y) dydx — j '=1     IQQ

3. Расчет поверхностной плотности тока на освещенной и теневой сторонах Ω

В [16] доказано, что с каждой стороны бесконечно тонкого идеально проводящего плоского экрана известны тангенциальная составляющая магнитного поля H _T и нормальная составляющая

электрического поля E n :

lim E„ ( x ) = + ¹— V_± J ( x );

X 3 —± 0 ⁿ 2 ros ^x

1 , .

lim H _T ( x ) = ±- J ( x ) x n .

x ₃ >± 0              2

Согласно принципу физического эквивалента [23], поля H ⁰ и H на поверхности идеально проводящего тела можно заменить эквивалентным поверхностным током J ^eq:

J ^eq = n X ( H ⁰ + H ),

— e ² j v j ( x ) j G ( x , y ) v j ( y ) d y d X > +

Q Q

^J

N Yr    , r          ,

+ X c j ' I J v- v j ( x ) j G ( x , y ) V- v e -( y ) d y d x — ^j '= 1    Y Q

— e ² j v j ( x ) j G ( x , y ) v e ' ( y ) d y d x

где n – нормаль к поверхности тела.

С учетом того что поле H ⁰ известно, а H =

= H ( x ) поддается вычислению для каждой T x ₃ >± 0

из сторон Q , подставив (13) в (14) при непрерывности падающего поля H ⁰, в пределе получим:

J0CB(x) = lim Jeq(x) = x 3 —>+0

= lim Tn x H0(x) + n x H (x)! = x 3 —+0 L                  T J

Q Q

= j f ( x ) v ^j ( x ) d x , Q

Xj Y j V- v e ( x ) j G ( x , y ) v- v j ( y ) d y d x —        (12)

j '= 1      I Q          Q

— e ² j v e ( x ) j G ( x , y ) v j ( y ) d y d x > +

Q Q

= n x H ⁰ ( x ) + n x| 1 J ( x ) x n J =

= n x H ⁰ ( x ) + ¹ J ( x ) «

« n X H ⁰ ( x ) + 1 J ( x ) = J ^0CB( x );

J ^TeH( x ) = lim J ^eq( x ) = ^x 3 ^{—— 0}

= lim Г—n x H0(x) — n x H (x x 3 ——0 L                  T

^J

N

+ X ce' ■ I j V- ve (x) j G(x, y)V- ve- (y) dydx — j '=1    Y Q

I 1 X I

= — n X H ⁰ ( x ) — n xl — —J ( x ) X n I =

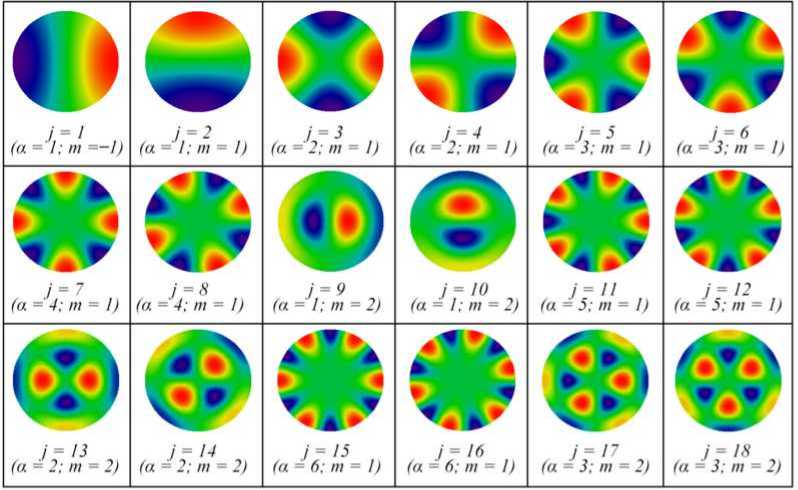
- min

а

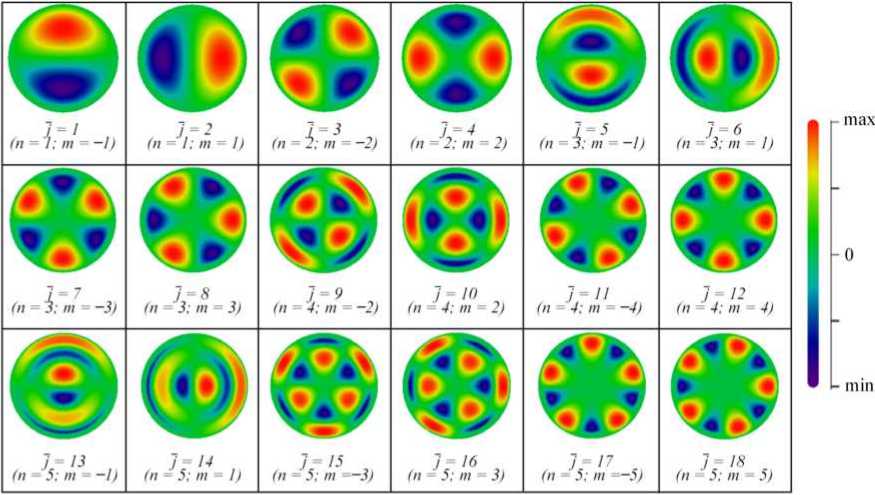
б

Рис. 3. Пример визуализации многочленов J ( x ) ( а ) и Z j ( x ) ( б Fig. 3. Example of polynomials visualization J-( x ) ( a ) and Z j ( x ) ( b )

= - n x H 0 ( x ) + 1 J ( x ) «

« - n x H 0 ( x ) + ¹ J ( x ) = J ^TeH( x ).

Таким образом, предложенный способ позволяет преодолеть ограничения (5) при асимптотическом выделении тока с каждой из сторон Q . Для сформированных представлений составим численную схему решения задачи (11), (12) при определении J ^0CB( x ), j ^TeH( x ) и выделении алгоритмических особенностей.

• 4.    Особенности алгоритмической реализации

Точность решения системы (11), (12) во многом зависит от численного вычисления одиночных и двойных интегралов. С этой целью представим область интегрирования Q многоугольником S е К ², ( х з = 0), состоящим из

M

S = U Ss s=1

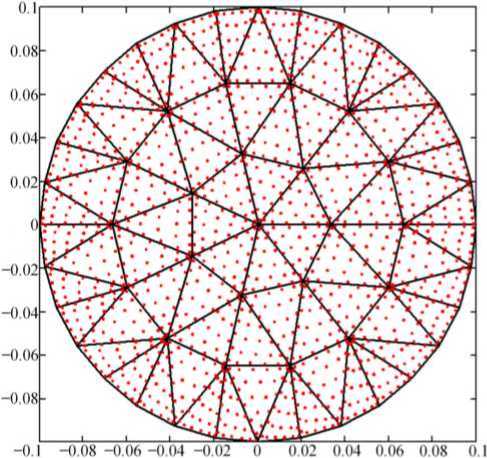
Рис. 4. Вариант представления диска П многоугольником S . Точками обозначены узлы численного интегрирования

Fig. 4. Variant of the disk representation Q by a polygon S . The dots indicate the nodes of numerical integration

треугольных областей таких, что

S m ⁿ S m ' = ^ ( m , m' ^G {1, M }, m * m ^^

Разбиение Q на треугольные элементы произведем триангуляцией Делоне (рис. 4) [6].

Окончательная система линейных алгебраических уравнений (СЛАУ) относительно неизвестных коэффициентов c e , c h примет вид

M

Е s = 1

MN   [„,

Е ЕcjИр'^h(x)JG(x,y)V . s '=1L j '=1        I SsS vj (y)dydX — в2 J vh (x) J G(x, y)v j (У)dУdx ’ +

Ss

а

б

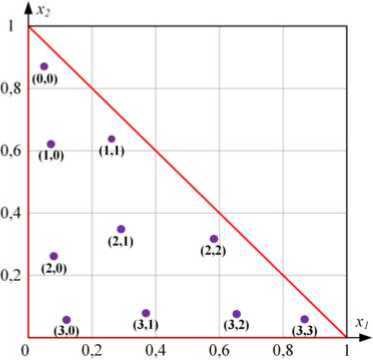
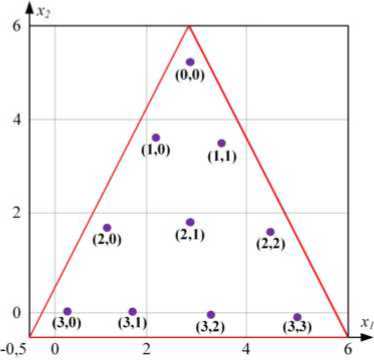
Рис. 5. Корни многочлена Дубинера - Курнвиндера при n = 4. Нумерация корней x _ai отображена в виде ( row , col ), где row -номер строки, col – номер столбца: a – на единичном треугольнике; б – на произвольном треугольнике

Fig. 5. Roots of the Dubiner–Koornwinder polynomial at n = 4. The numbering of the roots x a _b is shown in the form ( row,col ) , where row is the row number, col is the column number: a – on a unit triangle; b – on an arbitrary triangle

+ ЁА ]jV'Vh(x) J G(x,y)V-j=1      I Ss

■ v e ( y ) d y d x — в 2 J V h ( x ) J G ( x , y ) V e ' ( y )d y d x ’ =

Ss

M

= Е J f ( x ) V h ( x ) d x , s = 1 S_s

M

Е s = 1

MN   [..

Е ЕchИ Jv^e(x)JG(x,y)V . s '=1L j '=1        I SsS

■ V j ( y ) d y d x - в ² J V e ( x ) J G ( x , y ) V h ( y ) d y d x ’ +

Ss

+ Ё ce 'I J V^Ve (x) J G(x>y)V- j =1      I Ss

■ v e ( y ) d y d x - в ² J V e ( x ) J G ( x , y> у ( y ) d y d x ’ =

Ss

= E J f ( x ) v e ( x ) d x .

s = 1 S_s

Ввиду того что Q с К ² = ( x 3 = 0) с R ³, V^ V h ( x ) = 0 и

V^ v h -'( x ) = 0.

В качестве узлов численного интегрирования внутри каждого S_s используются корни многочленов Дубинера – Курнвиндера [21]:

а

б

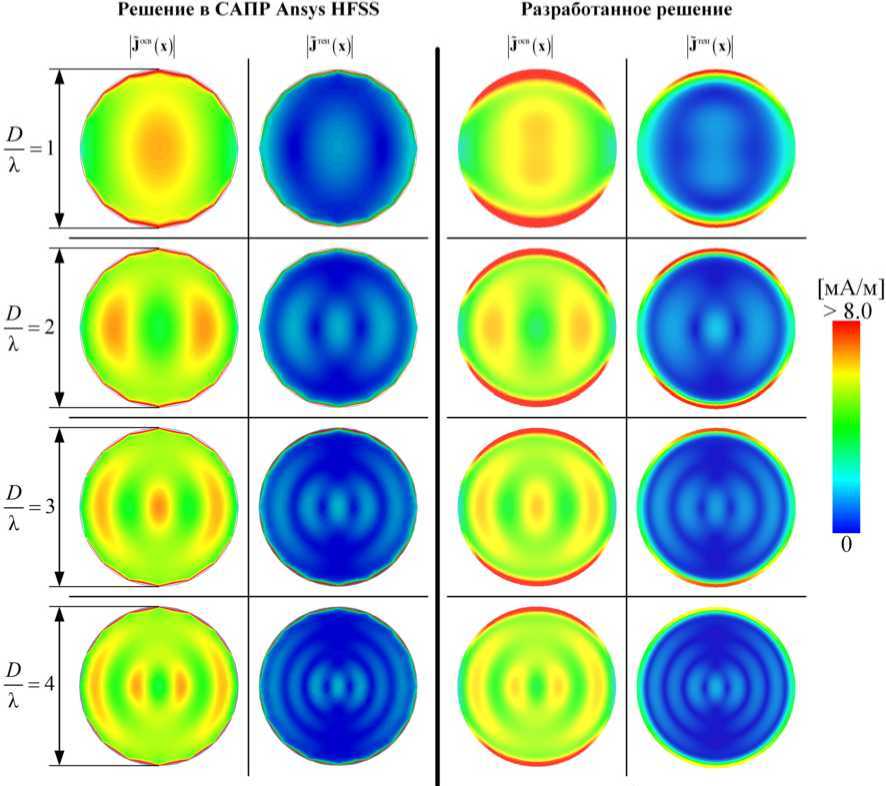
Рис. 6. Сравнение J ^OCB( x )| и J ^тен( х ) в САПР Ansys HFSS ( а ) и разработанного решениея ( б) при различных соотношениях D / X

Fig. 6. Comparison of J ^OCB( x )l and J ^TeH( x )l in Ansys HFSS CAD ( a ) and the developed solution ( b ) at different D/ X

Qn , k ⁽ x 1 ’ x 2 ) = P T^ X 1 )⁽¹ - x 1 ) k^Pk^0,0) ,x ² I ’    (19)

11 x 1J где n – максимальная степень многочлена Якоби

P n O^Hx ); 0 <  k <  n.

Координаты узлов интегрирования определим по правилу (рис. 5):

xa,b = {(x 1 ’x2(1 - x 1)) : x1 = (X1’ )b’ x 2 = (Xa ’ b)(n - b - a); 1 e E0’n - 0

b e[ 0, a J ; a , b , n e N 0 } ;

X a ’ ^b J x : j ^{( 2(} a ^- Ь J¹’ ⁰ ) ( x ) = 0;

1 I s Jn-(a - b)      s s e (0, n - (a - b));

x о <  x 1 < ... <  x n - ( a - b ) ; x s ^e К j ;

X 2 ^a ’ b = { x p : J n - b ⁾⁽ x p ) = 0; P e ^(0, n - ^b );

^x 0 <  ^x 1 < ... <  ^xn - b ;

^xp ^{e К} } .

В ходе вычисления (11) и (12) возникает ситуация, когда s = s' и x = y при |x - y| ^ 0 и G ( x , y ) ^» . Для исключения сингулярности в G ( x , y ) при s = s' интегрирование производится в полярной системе координат [22]. Обозначим S s = S s,= T s , тогда в интегралах вида

G ¹ j 1 ’ j 2

V-V; ( X )

j ₁ T_sT_s

_е М^x-y|

V-V; ( y ) d y d x ;

^{X -} y       j ²

G ² i = f V/ ^(x) ( e V,- ⁽ y ^{) d} y d^{x j} 1 ’ j 2           > 1 X - y j 2

TsTs

(где j 1 , > 2 - порядковые номера базисных функций) преобразуем по d y в локальную относительно T s полярную систему координат у ( ф , р ) с центром в х . В таком представлении (20) преобразуется:

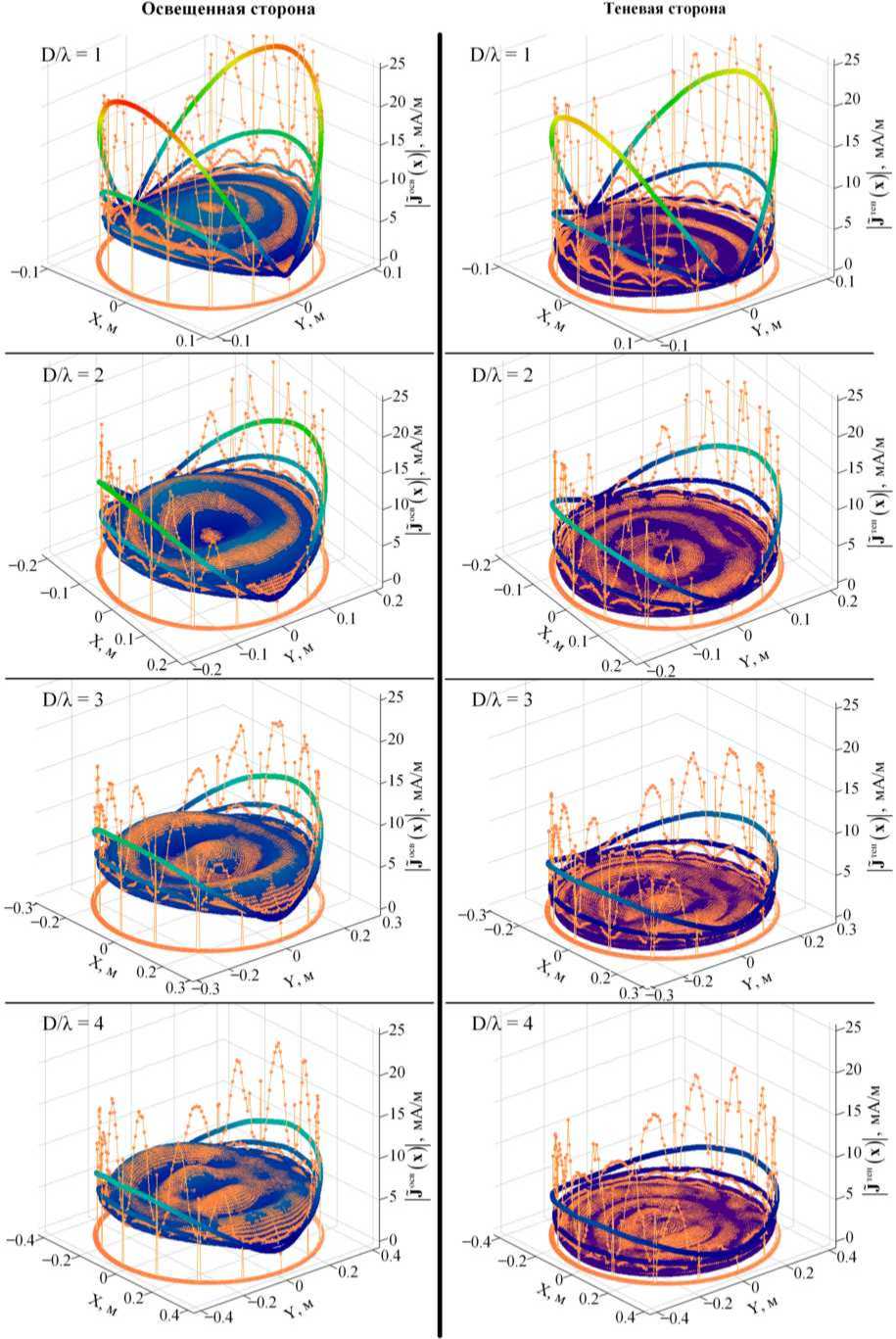
Рис. 7. Совмещение графиков J ^OCB( x ) и J ^TeH( x )| для различных соотношений D/ X . Оранжевый - САПР Ansoft HFSS, цветной -разработанное решение

Fig. 7. Matching plots j ^OCB( x ) and j ^TeH( x ) for different DI X . Orange - Ansoft HFSS CAD, colored - developed solution

а

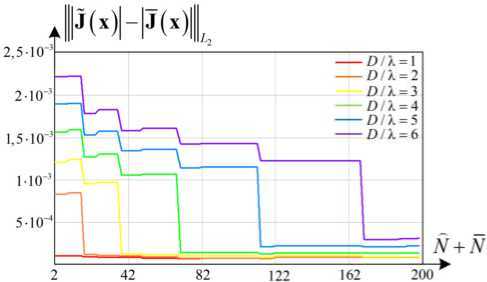
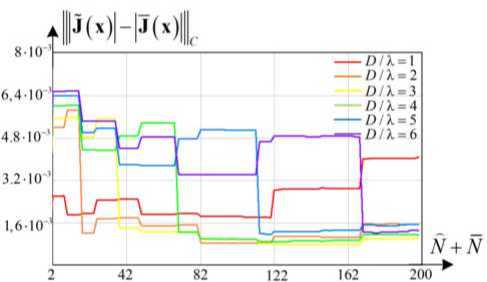
Рис. 8. Зависимость

Fig. 8. Dependence of

j ( x )| - J ( x )|||_L ( а ) и |||J ( x )| — I J ( x )|||_c ( б) от числа базисных функций

|J(x)| - J(x)|||_L ( a ) and ||J(x)| - |j(x)|||_c ( b ) on the number of basis functions

б

G ¹ j 1 , j 2

₂ ф q 1 r q W

Г'"<

Ts            q=0 ф q 0

■ Vj (У(ф, P)) dPdФdx;

G²

₂ф q 1 rq⁽ф)

= fvj (x)' Xf f ^ei^₽PVj (y(ф, P)) dPdфdx,

Ts   ¹     q=0 ф q 0         ²

где q - номер вершины Ts;

ф m = ^arctg

q x2 - x2

--------------------;

xq - x 1

y(P, ф) = (p cos ф + x 1, P sin ф + x₂);

R'

rq⁽ф) =       q ;

q     cos(ф-ф_q)

x ‘q ^ф=^arctg —_q x₁

^x 2 . ;

^{- x}1

X 'q =

C bqdq

-

aqcq

^-aqdq

-

bqcq

(aq )2 + (bq )2

(aq )2 + (bq )2 J

- координаты пересечения дx^qx^{q 1}x со стороной (X ^qX ^{q 1});

q1 q              q1 q aq x 2 x 2; bq x1 x 1;

cq = ^x11 ^x2q^{- x}21 xq ; dq = ^bqx1^-aqx2 ;

q1 = (q + 1)mod 3; Rq = lx' l - x|; x^q = (xq, xq)

- координаты вершин Ts.

Таким образом, указанные приемы позволяют минимизировать влияние ошибки численных методов расчета на получение итогового результата. Следует отметить, что точность получаемого решения значительно зависит от приближения границы многоугольника S к 5Q. С этой целью количество областей интегрирования необходимо увеличивать у границы S.

5. Результаты верификации сформированных решений

Для наглядной демонстрации предпочтительности сформированного решения выполним серию вычислительных экспериментов, которые предполагают получение плотности тока на освещенной и теневой сторонах диска для различных порядков аппроксимации полиномов и размеров диска, заданного соотношением D / X, X - длина волны.

Эталонная модель, используемая для верификации полученных результатов, разработана в САПР ANSYS HFSS. Она имеет форму идеально проводящего цилиндра высотой 0,0001 м и радиусом D. В качестве источника ЭМП задана плоская монохроматическая волна с частотой 1,5 ГГц и фронтом, параллельным диску. Установки программы: режим моделирования: HFSS IE Solver; Maximum Number of Passes: 20; Maximum Residual Error: 0,0002. Сравнение полученных результатов для различных соотношений D / X = {1,2,3,4} (X = const) приведены на рис. 6, 7.

Оценка апостериорной сходимости оценивалась относительно модуля

I J(x )| = J х) ■ J1 ( x ) + J₂( x) ■ J₂( x) + J₃( x) ■ J ₃(x)

по нормам:

L2^:|||^J(x)| ^-|^J(x)|| L = / f (I^J(x )| ^-|^J(x )| )²d^x,

²    Q\5Q

C: ||J(x >1 -lJ(x) C = ^xj lJ(x)l-lJx)l|, где 5Q :={x: |x - y| <5,y eSQ} при 5> 0.

В качестве эталона J(x) принято решение, сформированное в САПР Ansoft HFSS.

Из представленных на рис. 8 графических зависимостей следует, что не все базисные функции вносят одинаковый вклад в решение тестовой задачи. В этой связи на графиках наблюдаются «скачки» (рис. 8). Отдельные увеличения ошибки (особенно для малых D / X) по норме С при росте числа базисных функций связано с ошибочным нахождением в САПР Ansoft HFSS поверхностной плотности тока J( x) вблизи dQ (рис. 7). Также для улучшения сходимости при малых соотношениях D ё требуется дополнительная регуляризация СЛАУ. В реализованном алгоритме ее решение выполнено прямым методом.

В целом применение составленного алгоритмического решения при исследовании задачи дифракции на Q и выделении J^0CB(x), j^TeH(x) обеспечивает экспоненциальную сходимость по норме L2 и полиномиальной по норме в С.

Заключение

Полученные результаты позволяют сделать вывод о предпочтительном применении предложенной модификации функций Бесселя и Цернике при решении задачи дифракции на Q. Основное достоинство предлагаемой схемы состоит в разделении суммарной поверхностной плотности тока J(x) на две составляющие: на освещенной J^0CB( x)

и теневой J^TeH(х) сторонах Q. Применение векторных базисных функций у e (x) и у hi (x), основанных на многочленах (9) и (10), удовлетворяющих граничным условиям (6) и (7), позволяет учесть влияние E0 на Je (х) и J _h (х). В свою очередь, поле H⁰ формирует дополнительные поверхностные токи равной амплитуды, но разного направления с каждой из сторон Q, что в совокупности с принципом эквивалентности позволяет разделить J( х) на J ^0СВ( х) и J ^тен(х).

Следует уточнить, что применение стандартных норм L2 и C при x ∈Ω для оценки сходимости в рассматриваемой задаче является некорректным, что обуславливается граничными условиями J(x) вблизи ∂Ω при возникающей сингулярности [16]. В этой связи в нормах L2 и C для апостериорной оценки сходимости результатов численного решения выбрана модификация при x eQ \ 5Q. В последующих исследованиях для априорной оценки сходимости предполагается выбирать пространства Соболева [24].

Полученные результаты при применении метода конформных отображений [12] потенциально позволят обобщить полученные результаты на бо- лее сложные геометрические структуры, что и является направлением дальнейших исследований.