Вычислительное моделирование движения сжимаемой среды, генерируемой точечным источником

Использование методов численного решения прикладных задач механики сплошных сред с использованием вычислительной техники в настоящее время является основным способом построения решений краевых задач, включающих системы дифференциальных уравнений движения, неразрывности, энергии, теплопроводности, концентрации, состояния и прочих, с соответствующими начальными и граничными условиями. При исследовании подобных задач большее внимание уделяется конечноразностным методам [1–4], требующим относительно малых вычислительных ресурсов. Значительный интерес вызывают схемы факторизации эволюционных дифференциальных уравнений [5, 6], позволяющие «расщеплять» многомерные задачи на последовательности одномерных задач, что приводит к существенному повышению эффективности вычислительных алгоритмов. В ряде исследований [7–13] для решения задач движения сплошной среды используются методы конечных и граничных элементов с различными видами аппроксимации полей скорости, перемещения, плотности, давления, температуры и других характеристик.

Для решения прикладных задач механики сплошных сред интенсивно развивается и успешно применяется метод крупных частиц (метод Давыдова), позволяющий выполнять расчеты вихревых структур с учетом отрывных явлений, исследовать фильтрационные и

струйные [14] течения, газо- и гидродинамические потоки с большими перемещениями и соударяющимися поверхностями раздела, движение многокомпонентных [15, 16], сыпучих и деформируемых сред [17], течения сквозь проницаемые объекты [18] и многие другие процессы. С использованием системы уравнений Эйлера построены трехмерные вычислительные модели взаимодействия струй с поперечными потоками [19, 20], истечения газа из отверстий и каналов [21, 22], воздействия ударных волн на препятствия и границы раздела сред [23, 24, 25], влияния локализованных источников энергии и массы на газодинамические характеристики газовых потоков [26, 27].

Следует отметить, что вопросам сеточной аппроксимации областей, моделирующих источники количества движения, энергии и массы (отверстия, щели, локализованные источники, в том числе со сложной геометрией) при построении численных решений уделяется недостаточно внимания. В настоящей работе рассматриваются особенности движения сжимаемой среды из точечного источника, генерирующего поток массы с интенсивностью m и энергетической мощностью s . Решение такой задачи обусловлено необходимостью исследования характеристик газовых потоков, эмитируемых подвижными точечными источниками различной интенсивности [28] в произвольной пространственной области со сложной геометрией.

Система уравнений Эйлера, описывающая движение сплошной среды в области G (в дивергентной форме [17, 29, 30]), включает уравнения:

– неразрывности

^ + V^ ( p V ) = m 5 ( 0 ) ;

– движения dpV) + V^(pVV)+VP = 0;

S t

– энергии

^^ + V • ( p UV ) + V • ( PV ) = £5 ( 0 ) ; dt            ^{x                 x} '

– состояния (адиабатический процесс)

p ( k - 1 )( U - V • V/2 ) - P = 0.

Здесь обозначено: p — плотность среды; V - вектор скорости потока с компонентами V x , V y , V z ; P — давление; U — полная удельная энергия; k — показатель адиабаты; 5 () — дельта-функция Дирака.

В силу сферической симметрии движения среды рассматривается 1/8 часть конечной области G (Рис. 1). Предполагается, что источник находится в вершине рассматриваемого куба, имеющей координаты x = y = z = 0 . В начальный момент времени в области G известны распределения компонент вектора скорости, плотности и энергии: V_x ( 0, x, y, z ) = 0; V y ( 0, x, y, z ) = 0; V z ( 0, x, y, z ) = 0; p ( 0, x, y, z ) =p o ; U ( 0, x, y, z ) = U 0 ; x, y, z e G .

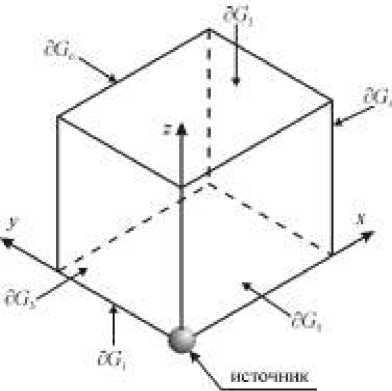
Рис. 1. Схема расчетной области и обозначения ее границ

Граничные условия определяются с учетом симметрии движения потока:

d V x /d z = 0, d V_y /d z = 0, V_z = 0, dp/d z = 0 , dU/d z = 0 , x, y, z g d G 1 ;

d V x /dz = 0, d V y /d z = 0, d V_z ]dz = 0, dp/ d z = 0 , dU/d z = 0 , x, y, z g d G 2 ;

V_x = 0, d V_y /dx = 0, d V_z\dx = 0, dp/ d x = 0, d U /d x = 0, x, y, z g d G 3 ;

d V_x /dx = 0 , d V_y /dx = 0, d V_z\dx = 0, dp/ d x = 0, dU/ d x = 0, x, y, z g d G 4 ;

d V x /d y = 0, V_y = 0, d V z /dy = 0, dp/d y = 0, d U/dy = 0, x, y, z gS G 5 ;

д V_x /d y = 0 , д V_y /d y = 0 , d ¥_z ^yy = 0, dp/d y = 0, dU/d y = 0, x, y, z g S G 6 .

Верификация результатов вычислительного моделирования выполняется с помощью точного решения стационарной ( dp/d t = 0 , dp U /d t = 0, dp V /d t = 0 ) системы уравнений (1)–(4)

V- ( p V ) = m 5 ( 0 ) ,

V- ( p VV ) + V P = 0,

V- ( p UV ) + V- ( PV ) = s5 ( 0 ) ,

p( k - 1)(U - V • V/ 2)-P = 0, которое имеет вид:

V = 2e/ m ;    p = Vm 3/ 4 n r ²V2 s ;    U = e/ m ;    P = 0 .

Граничные условия (5), заданные для «удаленных» границ d G₂, d G₄ и d G 6 при построении численного решения задачи (1)–(4) в области с ограниченными размерами, не вполне соответствуют точному решению (6), полученному для бесконечной области. При записи выражений (5) для всех искомых функций приняты

«мягкие» граничные условия [8], моделирующие установление течения сплошной среды на «удаленных» от источника границах расчетной области. Это, в известной степени, соответствует традиционным постановкам краевых задач механики жидкостей и газов [8, 9], в которых заранее не известен характер потоков жидкостей и газов вдали от источников возмущений.

Дополнительно следует отметить, что точное решение (6) для полной удельной энергии U = const удовлетворяет условиям (5) на всех «удаленных» границах:

d U _ d U _ d U _ 0

d x " dy ” dz” "

В соответствии с идеей метода крупных частиц [17] система уравнений (1)–(4) расщепляется по физическим процессам. Расчет каждого временного слоя разбивается на три этапа.

Для реализации первого (эйлерова) этапа считается, что изменяются лишь величины, относящиеся к ячейке в целом, а сплошная среда предполагается заторможенной. Система уравнений (1)–(3) представляется в виде:

р _ const, a z х

<

-(pV )+VP _ 0, ot

-( p U ) +V- ( PV ) _ 0"

o t

Уравнения этой системы записываются в виде явных конечно-разностных схем

ɶ

V , =v , ^r xijk ^r xijk

(⁷ i + 1/2 jk

^Pi - 1/2 jk ) ^ t

P ijk h x

,

ɶ

v yijk

= v yijk

⁽ P j + 1/2 k

^Pij - 1/2 k ) ^ t

P ijk h y

,

ɶ

V , =v , ^r zijk ^r zijk

( ijk + 1/2

P jk - 1/2 ) ^ t

P ijk h z

,

ɶ

U-, - U-, ijk ijk

& t  ( PV x ) , + ,/2j.

( ^PVx )_H / ₂ jk

^p ijk

h _x

+

+

PV

\ y iij + 1/2k

PV

\ y iij-Mkk

h y

+

( PV z ) jk + 1,2

(PV), ,„ z ijk -,/ 2

hz

.

В приведенных соотношениях величины с дробными индексами определяются как

^{( Л} ijk ^{+ Л} i ± 1 jk )

Л i±1/2 jk —        2’

_ ^(Л ijk ^{+ Л} ij + 1k )

Лу±1/2 k —

.          _ \ jk        ijk +1;

Лijk±1/2 —

где Л принимает значения: P; PV x ; PV y ; PV z .

На втором (лагранжевом) этапе вычисляются эффекты переноса, учитывающие обмен между ячейками при их перестройке на прежнюю эйлерову сетку. Определяются потоки массы за время A t через границы эйлеровых ячеек. Для учета направления движения сплошной среды потоки массы, импульса и полной удельной энергии определяются выражениями:

	~~ Л ijk V xi + 1/2 jk ,    Vxi + 1/2jk - 0 ,		~ Л i - 1 jk Vxi - 1 / 2 jk	~ ,    V xi - 1 / 2 jk - 0
x )i + 1/2 jk	~~	^V x l-- 1/2jk =		~
	_ Л i + 1 jk V xi + 1/2jk ,    Vxi + 1/2 jk <  0;		ijk xi - 1/2 jk ,	Vxi - 1/2 jk < 0 ;
	Л V     К   >0		Л V	V    > 0
	ijk yij + 1/2k ,     y yij + 1/2 k - v,		iV ij - 1kv yij - 1/2 k	yij - 1 /2 k -   ,
(Л VУ U k =]		(Л VУ ) j - 1/2k =<		~
	Л V      V    < 0- v i jk\kv + + 1/2 k , r yij + 1/2k <  v;		ijk yij - 1/2k ,	V     < O' y yij - 1/2 k < v;
	~~		~	~
	ijk zijk + 1/ 2 ,       zijk + 1/ 2         ,		Л ij - 1kVzijk - 1/2 ,	Vzijk - 1 /2 - 0,
(Л^ ) „. + 1/2 =j	~~	(лк )„ k - 1/2 j	~	~
	ь Л ijk + 1 V zijk + 1/2 ,   V zjk + 1/2 <  0 ;		Л ijk V zijk - 1/2 ,	V zijk - 1/2 < 0 "

В этих выражениях Л принимает значения: р ; p V x ; p V y ; p V z ; p U .

На третьем, заключительном, этапе окончательные значения массы, импульса и энергии в момент времени ^f = t + A t определяются законами сохранения массы, импульса и энергии, записанными с учетом промежуточных значений параметров потока:

+ ^V ( p V ) = 0,

<

£ ( p V ) +V. ( p VV ) = 0, d t ( p U~ ) +V- ( p UV ) = 0.

Разностная аппроксимация уравнений приводит к системе разрешающих соотношений:

^p «. =P k ^{- A} t [^{( p} V x ) , + „2 „ ^{- ( p} V A,, ,. ] [к ⁺

+r(pvj    -(pV;)    ^] A +F(pfJ    -(pV)   ^] hn_z L

_\     y hj + „2k \ y 'ij - ,2k J/ y _^V z^j'k + 12 ' z^jk - ,2 ]/ )

ˆ xijk xijk pijk ] pijk

( pVx V)

x ^x)i + 1j2 jk

- ^{(p V}x V x L jk ]/ ( ^p >A ^{) +} -

■ | i ^{p V;r} ) , . V2k "W> ) , - ,2k ]/ ( ^p A ' + ' '’ V- )„ k . „2   ( ' V ' ) j> - ,2 l/ i-V . h )•

ˆ yijk      yijkp,jk ] p,jk

pW)

\^{r y x}/i + 1/2jk

^-(pV/ x L, ]/ ^{( p} A ^{) +}

⁺ [ ( ^{p V}7 y ⁾„«/2k "H y^V ) ,-« ]/^{( p} -Л ) ■ '!’'/ ( jk .     ^{p P} )„ k - ,2 ]/^{( p} ,k^h )

/V           ~             у

ˆ zijk       zijkp,jk / p,jk

(pVzVx )

i + ,2 jk

^{-(p V}z V x L,2j« ]/ ^{( p} «*^hx ^{) +}

⁺ [ ( P ^Vz^V )„ V2. ^{-(p V}z^V' ) j - ,2k ^]/ ⁽ P ,k^h, ^{) +} [ ⁽ P ^Vz V; \_t .„, - ^{(p V}z^Vz I, - ,2 ^]/ ^{( p} .^ )

/V           ~            ]

ˆ ijk ppijk! p,jk

^{(p UV}x L jk ^{-(p UV}x ) , - V2j. ]/^{( p} j- h x ) ⁺

⁺ [⁽p ^UV ) j + „2k ^{- (} p ^UV )_№ k ^]/ ^{( p} «k N » + ( p ^UV ) ,j„ + ,2 ^{-(P U} V. ) _St . ^]/ ^{( p} .k h z ) • •

Поле давления вычисляется из уравнения состояния (4) с учетом поправки для обеспечения баланса энергии [17]:

ˆ               ˆ      ˆ              ˆ2     ˆ2      ˆ2

ijk \         ) ^p ijk \ ijk ^-    | xijk yijk zijk

₊ ^p ijk ^p ijk

ˆ xijk

xijk           yijk yijk           zijk

-

~  \2

V zijk )

По окончании третьего этапа в ячейке, где расположен источник (центр ячейки, моделирующей точечный источник, имеет координаты { h x /2, h y /2, h_z /2 } ), пересчитываются значения плотности и энергии в соответствии с уравнениями (1) и (3) с учетом заданных величин m и s :

^p jk ( ^ ) = ^p ijk

m A t

+ h_xh_yh_z

Ujk (t') =

P ijk U ijk ₊ sA t p jk (t')     h x h y h z p ijk ^{( P )} •

С использованием описанного алгоритма разработан комплекс программ для численного исследования пространственного движения сжимаемой среды. В выполненных вычислительных экспериментах линейный размер рассматриваемой области определяется длиной ребра куба (Рис. 1), равной 0,004 м. Остальные величины составляют: интенсивность источника сплошной среды m = 0,001 кг/с; мощность того же источника 8 = 3mRT/ 2, где 3RT/2 — удельная внутренняя энергия [30, 31], R — универсальная газовая постоянная, T — температура поступающей среды, принятая равной 300оК; показатель адиабаты к = 5/3; р0 = 0; U0 = 0. Для указанных значений определено, согласно (6), точное решение, которое обладает в пространстве сферической симметрией (центральной симметрией бесконечного порядка): V = 0,86502 -102м/с; р = 0,91995 -10-5 r-2 кг/м3; U = 0,37413 -104 Дж/кг; P = 0 Па.

Вычислительные эксперименты выполнены на равномерных (hx = hy = hz = h) сетках с количеством элементарных ячеек N = 6, 12, 25, 50 и 100 вдоль каждого из ребер куба, что соответствует 216 (при шаге интегрирования по времени At = 4,0 -10-8 с), 1728 (At = 2,0-10-8с), 15625 (At = 8,0-10-9с), 125-103 (At = 4,0-10-9с) и 106 (At = 2,0-10-9 с) расчетных ячеек соответственно. В каждом из вариантов расчеты осуществлялись до достижения состояния установления численного решения, при этом стационарность получаемого решения определялась выполнением условий maxi^jk "Л"Д <°Л .

• i,    j,k

Отклонения численных решений от точных значений (6) оценивались выражениями

• ^5Л = max |^Л У"к - ^Л ( x i , y j ’ z k )l • ⁽⁸⁾

В приведенных формулах обозначено: с_Л — заданная малая величина; n — номер временного слоя; Л _ijk — численное решение; Л ( x_i , y j , z_k ) — точное решение в расчетной ячейке с номерами i, j, к ( Л принимает значения р , U, P и модуля скорости V).

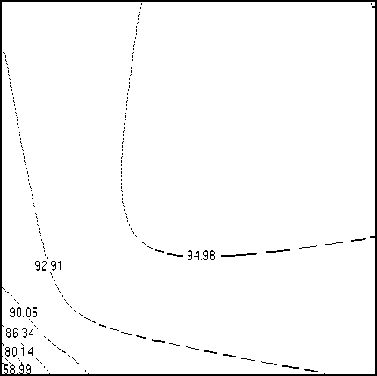
Результаты численного определения полей скорости, плотности, полной удельной энергии и давления движущейся среды в расчетной области G при использовании для аппроксимации 1728 и 10⁶ расчетных ячеек приведены на рисунках 2 и 3 соответственно. При использовании «грубой» сетки (Рис. 2) ячейка, аппроксимирующая источник, занимает около 0,5% объема расчетной области; применение разностной сетки, содержащей 10⁶ расчетных ячеек, приводит к уменьшению размера ячейки–источника движущейся среды до 0,0001% всего объема области G . Этим может быть объяснено существенное различие значений плотности в расчетной области, особенно вблизи «точечного» источника: за одинаковые промежутки времени в разные по объему ячейки-источники поступают равные массы генерируемой сплошной среды. По той же причине при использовании «грубой» сетки давление вблизи источника оказывается ниже, и, как следствие, снижается скорость потока (Рис. 2).

Вычислительные эксперименты показывают, что распределение значений полной удельной энергии мало зависит от параметров разностных сеток (в частности от размеров расчетных ячеек) в отличие от распределений значений скорости, плотности и давления, которые весьма существенно зависят от степени дискретизации расчетной области (Рис. 2 и 3). Следует также отметить наличие зависимостей найденных функций скорости, полной удельной энергии и давления движущейся среды от расстояния до источника и направления практически при всех используемых степенях дискретизации расчетной области (Рис. 2 и 3), что противоречит точному решению (6). Вычисленные значения плотности потока движущейся среды также зависят от направления (Рис. 2, а и 3, а ).

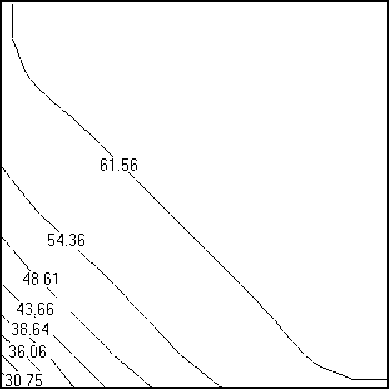
б

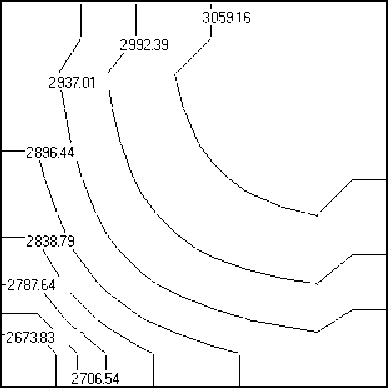
в                                                 г

Рис. 2. Распределения плотности, кг/м3 (а), модуля скорости, м/с (б), полной удельной энергии, Дж/кг (в) и давления, Па (г) в плоскости z = 0 при аппроксимациях исследуемой области с использованием 1728 расчетных ячеек

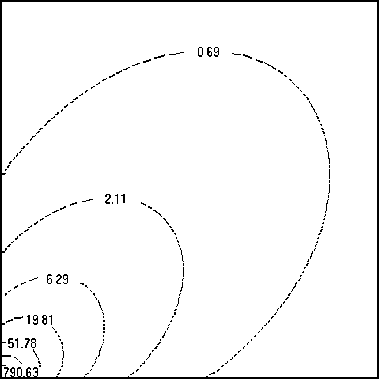
а

б

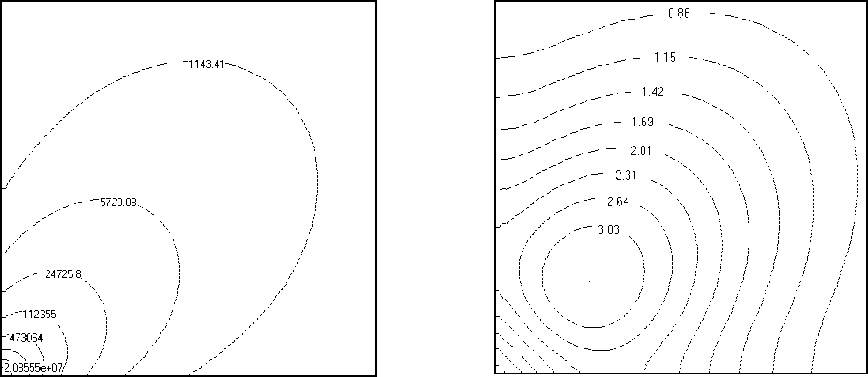
Рис. 3. Распределения плотности, кг/м3 (а), модуля скорости, м/с (б), полной удельной энергии, Дж/кг (в) и давления, Па (г) в плоскости z = 0 при аппроксимации исследуемой области с использованием 106 расчетных ячеек

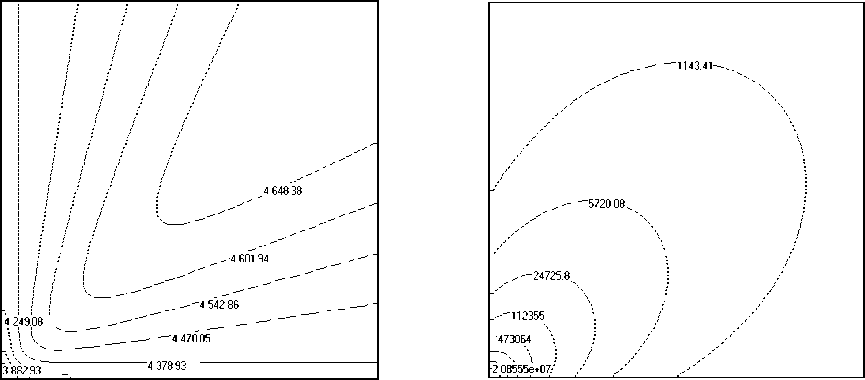
Рис. 3. Продолжение

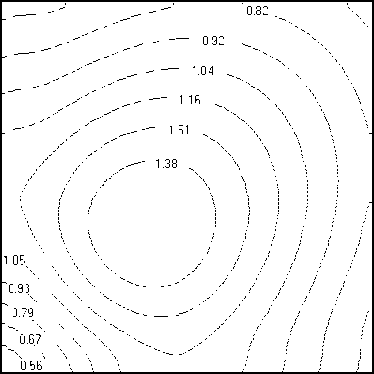
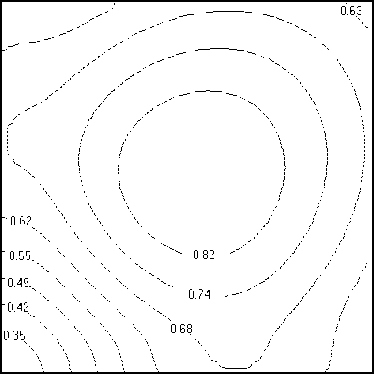
Особенности распределения плотности движущейся среды, приведенного на рисунке 4 для различных сечений расчетной области плоскостями z = const, указывают на наличие затопленной струи (об этом свидетельствуют концентрические изолинии плотности), генерируемой источником, что также противоречит точному решению рассматриваемой задачи. Анализ результатов вычислительного моделирования позволяет предположить, что отсутствие сферической симметрии в распределении характеристик потока определяется принятыми при проведении расчетов разрешающими соотношениями метода крупных частиц, полученными в предположении кубической формы расчетных ячеек, используемых для аппроксимации расчетной области.

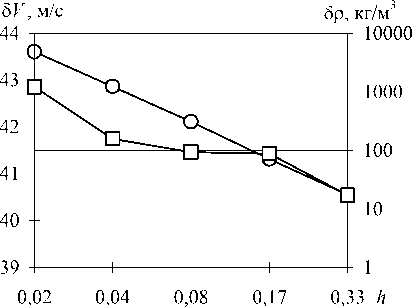
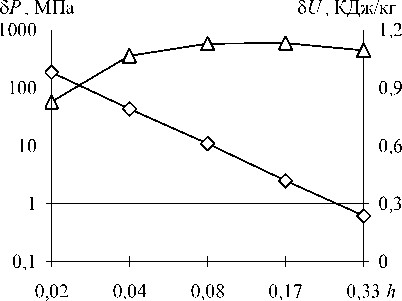
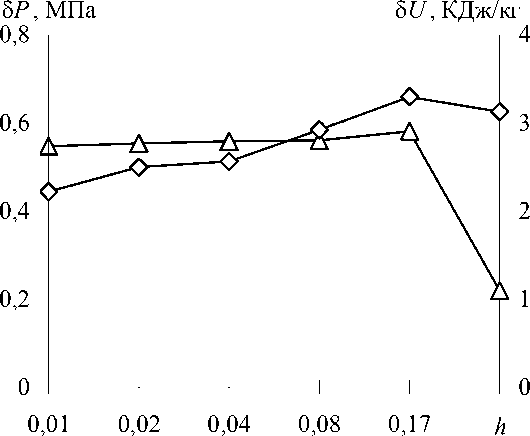
На рисунке 5 (а, б) показаны отклонения (8) численных решений от точных значений (6) в зависимости от степени дискретизации расчетной области. Следует отметить возрастание погрешностей (кроме полной удельной энергии) при повышении степени дискретизации расчетной области. На этом же рисунке (фрагменты в, г) приведены распределения погрешностей (8) численного решения в зависимости от расстояния r до источника, показывающие, что наибольшие погрешности сосредоточены вблизи источника и существенно уменьшаются по направлению к периферии расчетной области (на примере аппроксимации области с использованием 106 расчетных ячеек).

а                                         б

Рис. 4. Распределения плотности (кг/м3) в плоскостях z, мм: 0,5 (а), 1,0 (б), 1,5 (в) и 2,0 (в); аппроксимация исследуемой области с использованием 106 ячеек

в

г

Рис. 4. Продолжение

а

б

8 V, м/с

8p , кг/м³

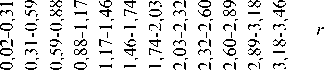
в

8 P, МПа                        8 U, КДж/кг

Рис. 5. Погрешности решения в зависимости от аппроксимации расчетной области (а, б), где h – размер ячейки, мм, и расстояния до источника r, мм (в, г):

плотность (-О-), скорость (- □ -), полная удельная энергия (- А -) и давление (- ◊ -)

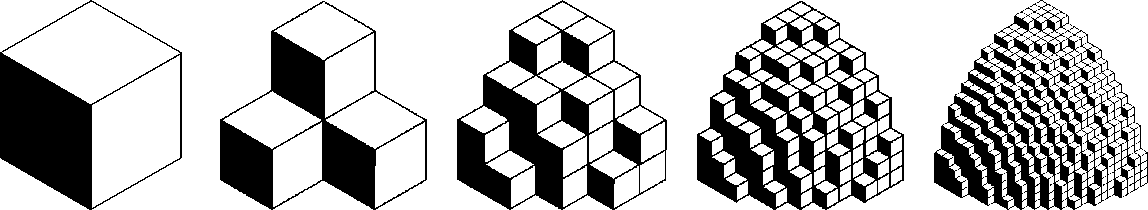
б

а

в

г

д

Рис. 6. Аппроксимация 1/8 части области, занятой точечным источником, с использованием 1 (а), 4 (б), 35 (в), 272 (г) и 2157 (д) расчетных ячеек

Для уточнения решения поставленной задачи (в частности для повышения степени симметрии в распределении численных решений) проведен ряд вычислительных экспериментов с применением аппроксимации зоны, моделирующей точечный источник набором расчетных ячеек. Вычислительные работы выполнены для той же области G с применением указанной ранее последовательности сеток; аппроксимация области, содержащей источник, проводилась с помощью 1, 4, 35, 272 и 2157 расчетных ячеек соответственно (Рис. 6).

Выбранная для расчетной области G последовательность разностных сеток позволяет повышать точность аппроксимации участка, занятого точечным источником, при сохранении размера этого участка в пределах от 0,5% (Рис. 6, а) до 0,2% (Рис. 6, д) объема всей области G. Для реализации соотношений (7) в этом случае величины m и s распределяются поровну по всем ячейкам, аппроксимирующим «точечный» источник.

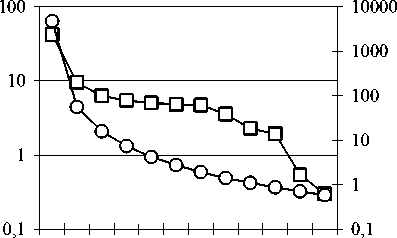
На рисунке 7 представлены отклонения численных решений от точных значений в зависимости от степени дискретизации расчетной области для указанной последовательности сеток с использованием аппроксимации источника сплошной среды. При этом точки, соответствующие шагу разностной сетки h = 0,33 мм, отвечают численному решению с аппроксимацией источника сплошной среды одной ячейкой (Рис. 6, а), то есть решению, приведенному на рисунке 2. В отличие от зависимостей, указанных на рисунке 5, при использовании аппроксимации зоны источника (Рис. 6, б-д) и повышении степени дискретизации расчетной области отмечается снижение погрешностей для всех искомых функций.

Рис. 7. Погрешности решения в зависимости от аппроксимации расчетной области при использовании аппроксимации точечного источника: плотность (-О-), скорость (- J -), полная удельная энергия (- Д -) и давление (- ◊ -); h - размер ячейки, мм

б

а

б

в

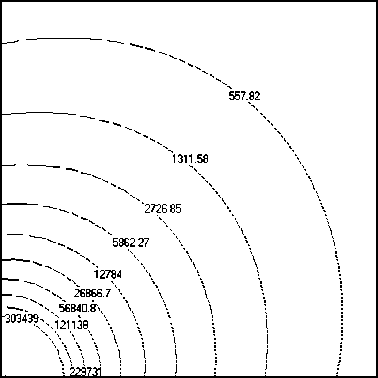
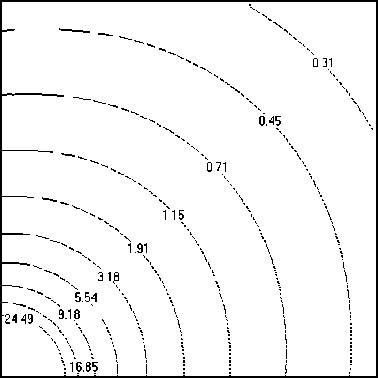
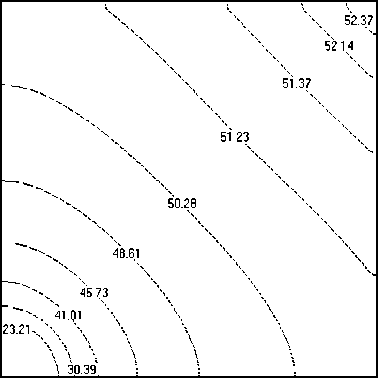
Рис. 8. Плотность, кг/м3 (а), модуль скорости, м/с (б), полная удельная энергия, Дж/кг (в) и давление, Па (г) в плоскости z = 0 при аппроксимации расчетной области и источника с использованием 106 расчетных ячеек

Распределение функций скорости, плотности, полной удельной энергии и давления для области G, содержащей 10⁶ ячеек, в сечении расчетной области плоскостью z = 0 представлено на рисунке 8. Приведенные поля искомых функций близки к сферически симметричным. Полученное распределение плотности показывает отсутствие затопленной струи, отмеченное ранее на рисунке 4. Следует отметить, что найденные распределения искомых функций ρ , V и U имеют более низкие значения по сравнению с точными решениями (6). Это объясняется тем, что характеристики точечного источника m и ε теперь распределяются по объему всех ячеек, аппроксимирующих этот источник, снижая тем самым интенсивность его воздействия на искомые решения.

Выводы

Комплекс программ, реализующий пространственный вариант метода крупных частиц, позволил выполнить сравнение точного решения задачи о движении сжимаемой среды, генерируемой точечным источником, и численного решения, полученного методом крупных частиц (методом Давыдова) с использованием последовательностей разностных сеток с уменьшающимися размерами расчетных ячеек. Погрешности численного решения достигают наибольшего значения вблизи источника и существенно уменьшаются в направлении к периферии расчетной области.

Выявлено отсутствие сферической симметрии численного решения при использовании расчетных ячеек кубической формы. Дополнительная аппроксимация источника конечным числом ячеек приводит к распределению искомых величин, близкому к сферической симметрии, и, одновременно, к понижению значений искомых функций по сравнению с точными значениями.