Вычислительное моделирование переноса и рассеяния воздушным потоком отработанных газов автотранспорта над территорией городского квартала

В настоящей работе рассматривается перенос и рассеяние над территорией городского квартала оксида углерода, входящего в состав отработанных газов автомобильного транспорта. Исследование такого процесса осложнено необходимостью учета элементов улично-дорожной планировки и характера застройки (расположения дорог и зданий, высоты и типа строений), направления и скорости движения воздушных масс, случайного характера появления автомобилей на проезжей части, нестационарности транспортных потоков и прочих факторов. В свою очередь, интенсивность транспортных потоков зависит от местонахождения городского квартала, расположения скоростных и транзитных дорог, особенностей размещения промышленных предприятий, автохозяйств, бензозаправочных станций и станций техобслуживания в рассматриваемом квартале и прилежащих к нему районах. Типичная схема застройки и транспортно-дорожной сети городского квартала показана на рисунке 1.

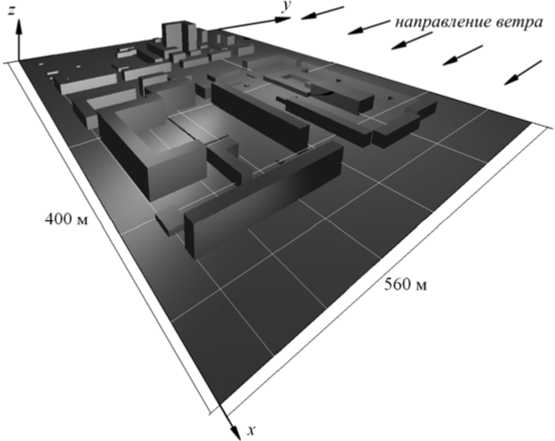
Рис. 1. Сеточная модель исследуемого городского квартала

Выбрасываемый подвижными точечными

В начальный момент времени в рассматриваемой области известны температура, плотность и давление воздуха, поле скорости движения воздушных масс. Поток транспортных средств моделируется как множество отдельных подвижных точечных источников загрязняющей примеси. Каждый точечный источник с известными значениями интенсивности и мощности эмитирует поток газа, содержащий пассивную газовую примесь. Скорость движения точечных источников, а также их количество задаются в соответствии с данными натурных наблюдений [12] за движением транспортного потока на рассматриваемых участках улиц городского квартала.

источниками газ смешивается с воздухом, и полученная газовоздушная смесь, увлекаемая воздушными потоками, переносится между зданиями и сооружениями. В общем случае на перенос и рассеяние газовой примеси оказывает влияние ее плотность. Кроме того, выбрасываемые автомобилем отработанные газы имеют более высокую температуру (и, соответственно, более низкую плотность по сравнению с атмосферным воздухом), что обеспечивает подъем газовой примеси в воздушном потоке за счет положительной плавучести отработанного газа. В то же время многие газы, входящие в состав выхлопных газов автомобильного транспорта, обладают удельным весом, превышающим удельный вес воздуха. Вследствие этого за счет отрицательной плавучести остывающая газовая примесь концентрируется в нижних слоях воздушного потока. Для учета указанного фактора используется приближение Буссинеска, согласно которому при малой концентрации C и малом отклонении температуры Т газовой примеси от среднего значения температуры воздушного потока применяется разложение функции плотности газовоздушной смеси р(C, Т) в ряд Тейлора:

р( C, Т ) = р( C0, То )+8р( C0, T) (C - C0 )+8р( C", T0) (T - To ) = Ро +а C+Р( T - То), (1) о C                 о T где С0 = 0, р0, T0 — начальные концентрация, плотность и температура газовоздушной смеси, а = 5р( C0, T0 )/д C — концентрационный коэффициент плотности, в = 5р(C0, T0 )/дT — температурный коэффициент объемного расширения газа.

С учетом этого математическая постановка задачи исследования переноса и рассеяния воздушным потоком отработанных газов автомобильного транспорта в сложной пространственной области включает в себя систему дифференциальных уравнений [13]

– неразрывности

Ip + V^p V ) = m 8 ( r _s ) ,

О t

– движения

^(PV) + V-(pVV ) + Vp = g [aC + p( T - To)] + m V. 8(r),(3)

О t

– полной удельной энергии

^^У+ V• (p UV)+ V •(p V)=-V •(Pg V)+ e 8(rs),(4)

– состояния

p(k - 1)(U - VV/2)-p = Pg.(5)

Для исследования концентрации отдельных компонентов газовоздушной смеси система уравнений (2)–(5) дополняется уравнением концентрации, записанным в диффузионном приближении:

-- + V. ( C V ) =V. ( XV C ) + q 8 ( r _s ) . d t

Здесь обозначено: V — вектор скорости воздушного потока; r _S — радиус-вектор положения точечного источника; g — ускорение свободного падения; U — полная удельная энергия газовоздушной смеси; P g — гидростатическое давление в воздушном потоке; p — отклонение действительного атмосферного давления от гидростатического; k — показатель адиабаты; e — мощность точечного источника; m — массовый расход отработанного газа, имеющего скорость V _m ; q — интенсивность поступления газовой примеси из источника; X — коэффициент диффузии примеси; 8 () — дельта-функция Дирака.

Построение разрешающих соотношений для численного решения системы дифференциальных уравнений (2)–(6) осуществляется на основе метода Давыдова (метода крупных частиц [14]). В разработанном на их базе комплексе программ [15] применяется технология параллельного программирования OpenMP. Комплекс прошел верификацию на точных решениях задач исследования движения потока сжимаемого вязкого нетеплопроводного газа [16] и переноса и рассеяния газовой примеси от подвижного точечного источника [10].

Численное решение задачи исследования движения воздушных масс, переноса и рассеяния отработанных газов автотранспорта в атмосферном воздухе над урбанизированной территорией находилось для квартала, сеточная модель которого показана на рисунке 1. Для получения достоверной качественной и количественной картины распределения концентрации газовой примеси от автотранспорта учитывался режим работы светофоров. Транспортные потоки по магистралям описывались моделью случайного процесса пуассоновского типа [ 17 ].

Вычислительный эксперимент выполнен для области с размерами 560 x 400 x 66 м; аппроксимирующая разностная сетка содержала 14,8 миллиона расчетных ячеек. Шаг по времени составлял 10^–3 с. Метеоусловия полагались нормальными: температура воздуха 275 К, на уровне поверхности z = 0 атмосферное давление 10 5 Па, плотность 1,2 кг/м³; коэффициенты диффузии X _x = X y = 67 м²/с, X _z = 26 м²/с (что соответствует классу «С» устойчивости атмосферы [ 18 ]). На входной границе y = y max , а также на боковых ( x = 0, x = x max ) и верхней ( z = z max ) границах поддерживались значения компонент вектора скорости ( V_x = 0, V y = 0, V_z =- 6,0 м/с), плотности (1,2 кг/м³), энергии (соответствовала температуре 275 К), концентрации ( C = 0 кг/м³), отклонения давления ( p = 0 Па) и направление ветра (см . Рис. 1). На выходной границе y = 0 задавались условия переноса всех искомых величин: б V_x /6 x = 0, б V y ]б x = 0, б V_z/б x = 0, бр) б x = 0, б U /б x = 0, б p /б x = 0, б С/ б x = 0. Нижняя граница z = 0, а также стены и крыши городских зданий и строений моделировались условиями отсутствия скорости ( V = 0), потоков плотности, концентрации и энергии через эти границы . В начальный момент времени в рассматриваемой области (Рис. 1) задавались распределения компонент вектора скорости, плотности, энергии, давления и концентрации, соответствующие значениям на входной границе. Принималось, что каждый подвижный точечный источник эмитирует поток отработанных газов, содержащий угарный газ с плотностью 1,3 кг/м³, интенсивностью 0,12 г/с [19] и температурой 355 К.

На рисунках 2–4 представлены распределения изолиний скорости воздушного потока в характерных сечениях исследуемой области. Рисунки свидетельствуют, что воздушный поток, встречая на своем пути препятствие в виде городских построек, обтекает их как в горизонтальном, так и в вертикальном направлениях. Это существенно отличает разработанную пространственную модель от двумерных аналогов.

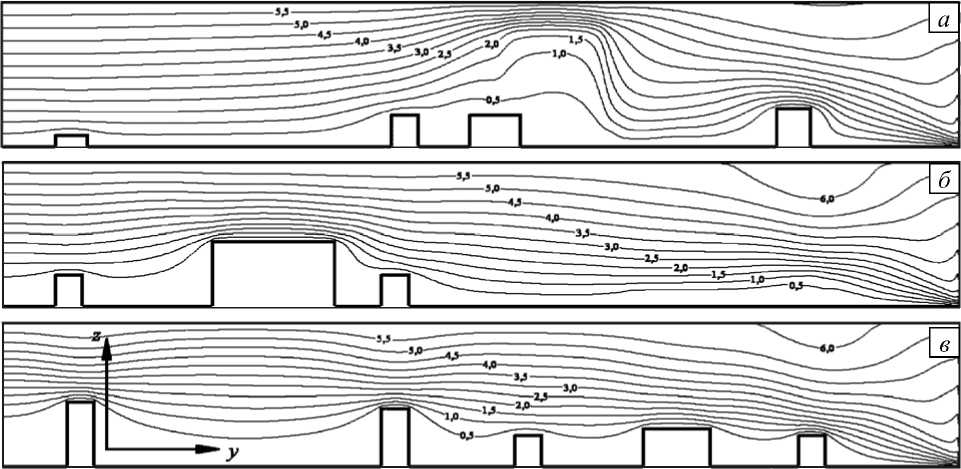
Рис. 2. Скорость газовоздушной смеси (м/с) в сечениях x , м: 100 ( а ), 300 ( б ), 400 ( в )

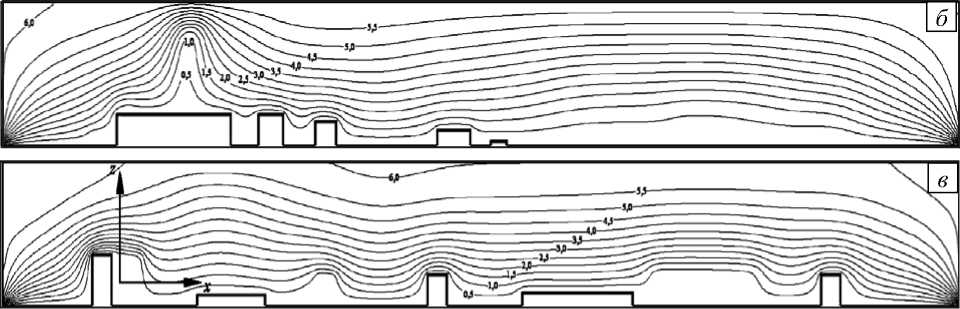
Рис. 3. Продолжение

На открытых участках городского квартала (на улицах, вдоль которых перемещаются воздушные массы, больших территориях без застроек, а также в тоннелях–путепроводах под домами, узких проходах между постройками) воздушный поток обладает большей скоростью, чем поток, движущийся внутри дворов и в областях плотной застройки. Отмечается наличие застойных зон с подветренной стороны зданий (Рис. 2–4) и в зонах плотной застройки (Рис. 2, в ; 3, б ; 4), градиенты скорости с наветренной стороны и над крышами зданий (Рис. 2, а , в ; 4, б , в , г ).

С ростом вертикальной координаты наблюдается увеличение скорости воздушного потока (Рис. 4). Это обусловлено как граничными условиями на подстилающей поверхности, так и тем, что на верхних уровнях городского квартала имеются значительные области, свободные от построек (зоны свободного движения воздушных масс). Результаты расчета хорошо согласуются с естественным представлением об обтекании воздушным потоком препятствий (зданий и сооружений).

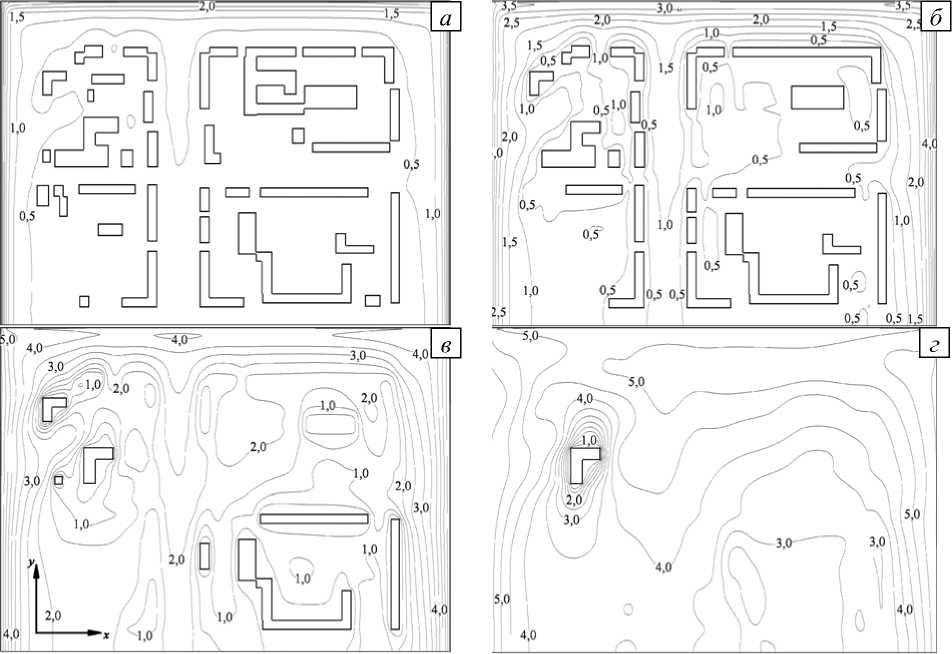
Рис. 4. Скорость газовоздушной смеси (м/с) в сечениях z , м: 5 ( а ), 10 ( б ), 20 ( в ), 40 ( г )

Поля концентраций угарного газа в городском квартале представлены на рисунках 5–7. Угарный газ благодаря переносу и рассеянию воздушным потоком распространяется практически по всей пространственной области. Застройка исследуемого городского квартала оказывает определяющее влияние на его рассеивание.

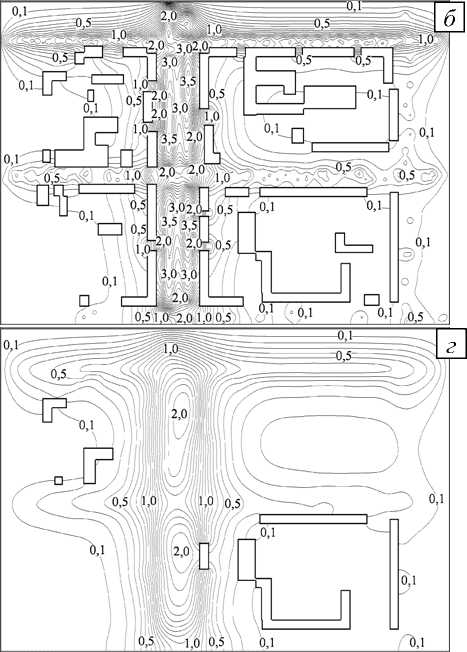
Городские здания и сооружения, расположенные вдоль транспортных магистралей, препятствуют прониканию загрязнений в воздушную среду дворовых территорий (Рис. 5, 6). Лишь небольшие объемы примесей, увлекаемые воздушным потоком, переносятся внутрь квартала через тоннели–путепроводы домов и проходы между постройками. Относительно высокая концентрация выхлопных газов (в данном случае угарного газа) от потока транспортных средств наблюдается вблизи построек со стороны проезжих частей квартала (Рис. 7, б – г ). Наибольшая же концентрация угарного газа, как показывают расчеты, сосредоточена в приземных слоях в непосредственной близости от транспортных магистралей (Рис. 6 и 7, а , б ). С увеличением высоты концентрация загрязняющего вещества существенно понижается (Рис. 7).

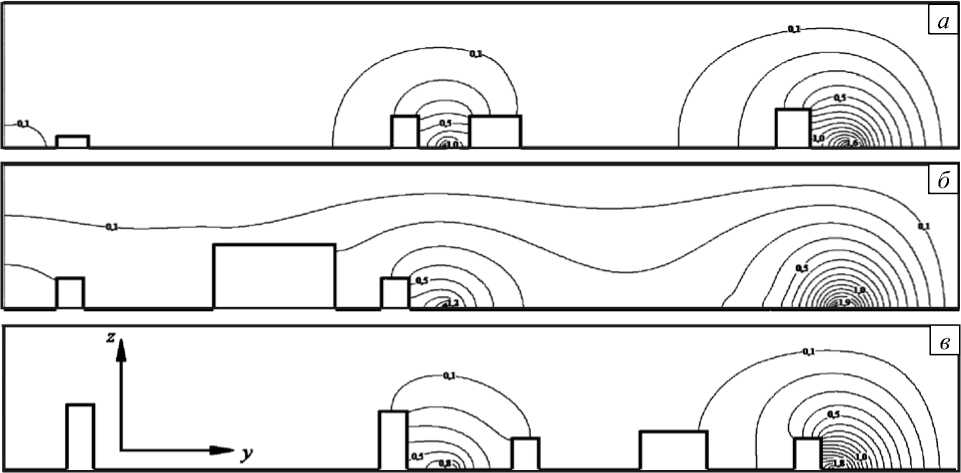
Рис. 5. Концентрация угарного газа (мг/м³) в сечениях x , м: 100 ( а ), 300 ( б ), 400 ( в )

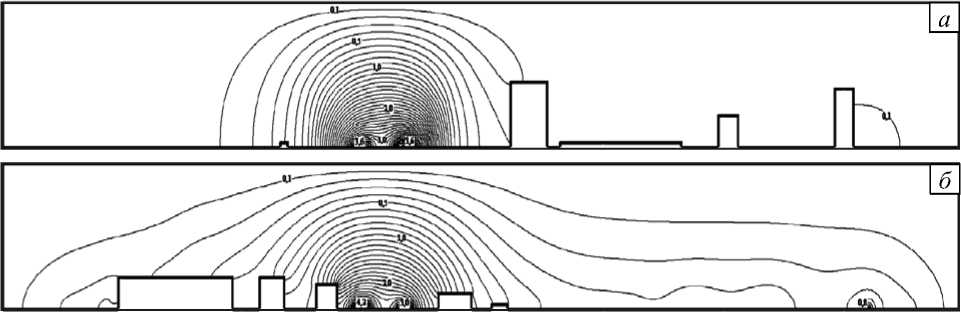
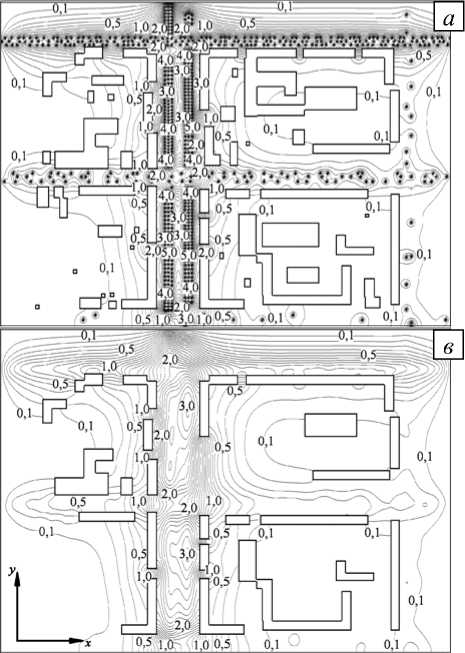
Рис. 7. Концентрация угарного газа (мг/м³) в сечениях z , м: 2 ( а ), 5 ( б ), 10 ( в ), 20 ( г )

Анализ результатов показывает, что концентрация газовой примеси (в пределах 6,0 мг/м3) и повышение температуры газовоздушной смеси от поступающих горячих отработанных газов (в пределах 7,0–10,0 К) можно признать малыми, что подтверждает обоснованность использования разложения (1) плотности газовоздушной смеси в ряд Тейлора при решении в приближении Буссинеска.

Выводы

Математическая модель, базирующаяся на системе уравнений Эйлера, дополненной уравнением концентрации (диффузионное приближение), учитывала случайный характер появления автотранспорта на границах рассматриваемого квартала, а также режимы работы светофоров. Транспортные потоки описывались случайным пуассоновским процессом. Вычислительная модель, включающая перенос и рассеяние газовой примеси (на примере угарного газа) в сложной пространственной области, содержащей здания, сооружения и транспортные магистрали квартала современного города, позволила определить поля основных газодинамических характеристик потока газовоздушной смеси и распределение концентрации газовой примеси.

Для компьютерной реализации использовался алгоритм метода Давыдова (крупных частиц), а также технология параллельного программирования OpenMP. Верификация программного комплекса осуществлялась на точных решениях задач движения потока сжимаемого вязкого нетеплопроводного газа и переноса и рассеяния газовой примеси от подвижного точечного источника.

Разработанная компьютерная модель может быть использована для создания инструментария, пригодного для объективного и обоснованного принятия решений по рационализации транспортных потоков, реконструкции дорог, проектированию и строительству новых транспортных магистралей с целью снижения техногенной нагрузки на атмосферный воздух городской территории.