Выделение и сравнение точечных особенностей на изображениях объекта

Постановка задачи

Реконструкция трехмерных сцен по набору изображений – одна из самых важных задач компьютерного зрения, имеющая множество практических применений [1]. Существует достаточно большое количество алгоритмов реконструкции, которые непосредственно зависят от типа решаемой задачи. У всех этих алгоритмов можно выделить некоторые общие этапы, которые обязательно должны быть реализованы:

• -    поиск особенных точек на каждом изображении набора;

• -    для каждой особенной точки уточняется регион, в пределах которого особенная точка однозначно локализуется и вычисляется некоторый количественный описатель – дескриптор;

• -    с помощью алгоритмов сравнения устанавливается первичное – строгое соответствие между особенными точками;

• -    построение фундаментальной матрицы;

• -    вычисление соответствий для незадейство-ванных особенных точек;

• -    вычисление трехмерных координат точек сцены и объединение их в так называемое облако точек;

• -    соединение облака точек в трехмерную модель;

• -    текстурирование трехмерной модели.

Особенная точка (точечная особенность, POI) – такая точка на поверхности объекта (сцены), которую можно легко выделить и локализовать на изображении. В идеальном случае особенная точка легко локализуется на каждом изображении набора, который может быть получен, например, телевизионной съемкой объекта с разных ракурсов. Регионом особенности называется область изображения, в пределах которой особенная точ- ка одного изображения может быть найдена на другом изображении. Регион характеризуется направлением градиента.

Для реализации быстрого и точного алгоритма трехмерной реконструкции объектов необходимо провести анализ существующих методов выделения точечных особенностей и способов нахождения между ними соответствий, выработать необходимые метрики количественного и качественного сравнения алгоритмов.

Существующие алгоритмы сравнения устанавливают соответствие особенных точек с помощью дескрипторов, вычисляя евклидово расстояние. Установкой некоторого порога можно отбросить ложные соответствия – оставить только точки с устойчивыми соответствиями. Но при этом из 500-700 точек остается только 10-15%, в результате чего можно будет построить только «разреженную» модель. Для построения «плотной», более точной модели необходимо разработать рекурсивный алгоритм сравнения, позволяющий не просто отбрасывать ложные соответствия, а уточнять их верными соответствиями.

Таким образом, можно сделать вывод, что третий и пятый по счету этапы алгоритма реконструкции в большей степени влияют на точность построения трехмерной модели объекта (сцены). В настоящей работе будет рассмотрен алгоритм, позволяющий улучшить качество сравнения особенных точек. Чем больше особенностей будут иметь верные соответствия, тем более точным будет алгоритм реконструкции.

Точечные особенности сцены

Особенности объекта (сцены) можно разделить на несколько видов. Особенностями первого рода являются конкретные области на изображениях: вершины, углы, различные орнаменты, выделяющиеся неоднородности и другие хорошо заметные, легко локализуемые особенности. Эти виды локализованных особенностей называют ключевыми точками (keyponts). Особенности второго рода – это грани. Такие особенности могут быть согласованы по их ориентации, локальной частоте появлений (краевой профиль) и могут быть хорошими индикаторами границы объекта и взаимных перекрытий объектов в последовательности изображений [1].

Преимуществом ключевых точек является то, что они позволяют установить соответствие даже в присутствии шумов, изменении масштаба или ориентации.

Существует два основных подхода для нахождения точечных особенностей и их соответствий

• [2]. Первый подход основан на нахождении особенностей на одном изображении, которые затем можно точно отслеживать с помощью техник локального поиска, таких как метод корреляции или наименьших квадратов. Данный подход используется, когда изображения набора получены с незначительно отличающихся ракурсов или взяты из быстрой последовательности при динамических изображениях. Второй подход использует независимое обнаружение особенностей на всех рассматриваемых изображениях набора и сравнение их с использованием местных дескрипторов. Применяется, когда изображения получены с достаточно сильно отличающихся ракурсов или с большим временным интервалом, в результате чего соответственные точки на изображениях оказываются сильно смещены.

Обнаружение ключевых особенностей и их сравнение можно разделить на четыре стадии:

• -    обнаружение (извлечение) признаков (отличительных характеристик) на изображении. На каждом изображении производится поиск регионов, которые могут быть легко обнаружены на других изображениях;

• -    каждый регион вокруг обнаруженных признаков конвертируется в более компактный и инвариантный количественный дескриптор, который может быть однозначно сопоставлен с другими дескрипторами;

• -    поиск наиболее вероятных соответствий между признаками на других изображениях;

• -    альтернатива третьей стадии, где поиск ведется только в малой окрестности каждой обнаруженной особенности и больше подходит для обработки видеопотоков.

Примером алгоритма, совмещающего все четыре стадии, является алгоритм SIFT (Scale Invariant Feature Transform) – масштабно-инвариантное преобразование особенности [3].

Обнаружение точечных особенностей

Точечные особенности проще локализовать на участках изображения с большими изменениями контраста (градиента) [2]. На рис.1 представлено изображение тестового объекта, а на рис. 2, того же объекта с локализованными особенностями.

При выделении особенностей заранее неизвестно, с какими особенностями будет происходить сравнение на другом изображении. Таким образом, можно только вычислить, насколько устойчива эта метрика в отношении малых изменений ^u , путем сравнения регионов изображений друг с другом. Эта метрика известна как автокорреляционная функция или поверхность:

Еде № = S wUi ^о <х; + Аг/) - к (^, )]2 > где ЕАС – автокорреляционная функция; \и – вектор смещения регионов (в пикселях); ™1хд – весовая функция региона x, индекс i означает применение весовой функции ко всем пикселям региона; Io – текущее изображение (массив значений яркости каждого пикселя).

Рис. 1. Изображение тестового объекта

Рис. 2. Выделенные точечные особенности

Для определения ориентации особенности необходимо вычислить градиент изображения. Это можно выполнить различными методами. Классический детектор Харриса использует фильтр. Более современные варианты используют сверт- ку по горизонтали и вертикали с помощью произ- водных Гаусса. Автокорреляционную матрицу А можно записать как А = и- *

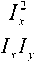
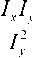
где взве-

шенные суммы заменены дискретной сверткой с ядром взвешивания w.

Матрица, обратная матрице A, обеспечивает нижнюю границу неопределенности расположения соответствующего региона. Это может быть полезным индикатором того, какие регионы могут быть надежно сопоставлены. Самый простой способ визуализировать и сделать вывод об этой неопределенности – это выполнить анализ на собственные значения автокорреляционной матрицы A, который состоит из двух собственных значений и двух собственных векторов направлений. Поскольку большая неопределенность зависит от меньшего собственного значения, то для нахождения хороших признаков необходимо найти максимумы в меньшем собственном значении.

Дескрипторы особенностей

Для поиска соответствий, обнаруженных на наборе изображений особенностей, их необходимо сравнивать между собой, то есть найти особенности на одном изображении и найти их соответствующее местоположение на другом изображении. В большинстве случаев локальный вид особенностей изменяется при смене масштаба, ориентации, при аффинных преобразованиях и т.д. Чтобы иметь возможность сравнивать особенности даже после различных преобразований, из региона особенности извлекается масштаб, ориентация, делается аффинная оценка, и вся эта информация используется для формирования дескриптора особенности. Но даже после компенсации этих преобразований вид регионов особенностей в последовательности изображений может изменяться [3].

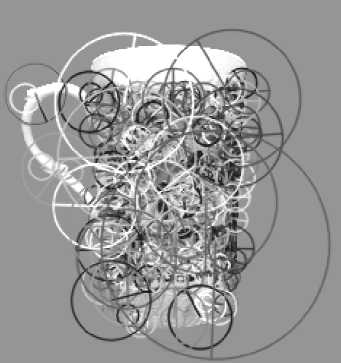
Рис. 3. Регионы особенностей

На рис. 3 изображены особенности с соответствующими регионами. Радиус окружности, ограничивающей регион, определяет масштаб, в котором особенность хорошо локализуется, прямая линия, направленная по радиусу окружности, показывает общее направление градиента региона.

Из этого следует, что дескриптор особенности должен быть максимально инвариантным ко всем этим преобразованиям, сохраняя при этом отличительные черты между разными регионами [1]. Значение дескриптора уникально для каждого алгоритма, но в общем случае это вектор значений. Количество значений в векторе может быть 32, 64 или 128 значений. Тип значений – целое (со знаком или без знака) или вещественное с плавающей запятой.

Рассмотрим дескриптор алгоритма SIFT. Каждый дескриптор представляет собой вектор из 128 элементов типа float (с плавающей запятой). SIFT дескриптор формируется вычислением градиента в каждом пикселе региона особенности (регион особенности в данном случае представляет из себя окно размером 16×16 пикселей), используя соответствующий уровень пирамиды

Гаусса, на котором была найдена особенность. Величина градиента затем уменьшается на значение Гауссовой функции спада для снижения влияния градиентов, расположенных далеко от центра, так как они более подвержены шуму. Далее в каждом квадранте размера 4×4 пикселя формируется гистограмма ориентации градиента – к одному из 8 значений гистограммы (histogram bins) добавляется взвешенное значение градиента. Для уменьшения эффекта положения и доминирующего направления каждый из 256 значений градиента сглаживаются трилинейной интерполяцией.

Оставшиеся 128 неотрицательных значений формируют основу дескриптора SIFT. Для уменьшения эффекта контраста значения вектора нормируются. Для того, чтобы дескриптор был устойчивыми к другим фотометрическим вариациям, значения вектора урезаются на 0,2 и результирующий вектор снова нормируется.

Сравнение особенностей

После извлечения особенностей и их дескрипторов из нескольких изображений необходим следующий шаг – установление некоторых предварительных соответствий между особенностями этих изображений. На рис. 4 прямыми линиями показаны соответствия между особенностями, найденными на двух изображениях тестового объекта.

Рис. 4. Соответствия между особенностями (порог 0,3)

Параллельные линии указывают на правильно обнаруженные соответствия, линии, расположенные под углом, указывают на неправильно установленные соответствия. Точки, для которых не найдено соответствий, оставлены без соединяющих линий.

Проблему установления соответствия между особенностями можно разделить на две составляющие: необходимость выбора соответствующей стратегии, которая определяет, какие соответствия должны передаваться следующему этапу для дальнейшей обработки, и разработка эффективных структур данных и алгоритмов быстрого поиска соответствий [1].

Стратегии сравнения

Определить, какие совпадающие особенности допустимы для дальнейшей обработки, зависит от контекста, в котором выполняется сравнение. Например, есть два изображения, которые перекрываются на 80%. Известно, что большинство особенностей на одном изображении будет совпадать с особенностями на другом изображении, но некоторые совпадать не будут, так как могут быть перекрыты или их положение изменится слишком сильно. С другой стороны, при попытке распознать, сколько объектов содержится в хаотической сцене, большинство из особенностей не совпадут.

Для многих алгоритмов сравнения необходимо, чтобы дескрипторы особенности были разработаны так, чтобы евклидово расстояние (векторная величина) в пространстве особенности можно было непосредственно использовать для ранжирования особенностей. Если оказывается, что определенные параметры (оси) в дескрипторе более надежны, чем другие, то рекомендуется перемасштабировать эти оси во времени для определения степени их изменения при сравнении с другими надежными совпадениями. Более общий процесс включает в себя процесс преобразования векторов признаков в новый базис масштабирования.

Учитывая евклидово расстояние в качестве метрики, простейшая стратегия сравнения устанавливает порог (максимальное расстояние) и возвращает результат сравнения с другими изображениями в соответствии с порогом. Установка более высокого порога, приводит к частым отрицательным срабатываниям, то есть возвращению неправильного соответствия. В свою очередь, установка слишком низкого порога приводит к частым ложным несрабатываниям, то есть много корректных соответствий будут пропущены. Сравнив рис. 4 и рис. 5, можно заметить, что снижение порога позволило отбросить неверные соответствия, но в то же время многие верные соответствия так же были отброшены.

Для ранжирования алгоритмов сравнения необходимо ввести количественные характеристики их производительности при определенном пороге. Подсчет количества истинных и ложных соответствий и несоответствий можно выполнить, используя следующие определения:

• -    ТР (true positives) – количество верных соответствий;

• -    FN (false negatives) – соответствия, которые не были обнаружены;

• -    FP (false positives) – количество неверных соответствий;

• -    TN (true negatives) – несоответствия, которые были правильно отклонены.

Эти значения необходимо перевести в удельные величины (УВ), используя следующие преобразования:

• -    УВ верных соответствий

  TP TP

  
  

  TPR =

  
  

  _-

  
  

TP + FNP

УВ неверных соответствий

FP FP

FPR =-------=;

FP + TN N

• -    положительное спрогнозированное значение

TP + TN p' ’ TP + TN - точность ACC =,

P + N где P – число соответствий, N – число несоответствий, p’ – предсказанное число соответствий.

Любая стратегия сравнения (с определенным порогом или параметром) может быть оценена с помощью TPR и FPR. В идеале, TPR должен стремиться к 1, а FPR стремиться к 0. При изменении порога сравнения получается семейство точек, которые известны как накопитель рабочих характеристик (ROC – Receiver Operating Characteristic). Это кривая (см. рис. 6), применяемая для организации классификаторов и визуализации их производительности. Чем ближе эта кривая находится к левому верхнему углу, тем выше производительность [1].

Рис. 5. Соответствия между особенностями (порог 0,15)

Кривая ROC также может использоваться для вычисления средней точности, которая является средней точностью значения PPV и зависит от порога.

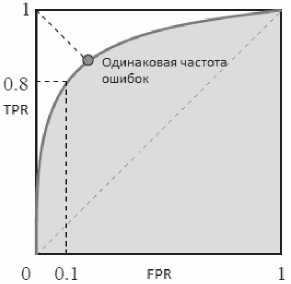
Рис. 6. Кривая ROC

Проблема с использованием фиксированного порога состоит в том, что его трудно подобрать. Полезный диапазон может изменяться в широких пределах для разных частей региона особенности. Лучшей стратегией в этом случае может быть простое сравнивание соседей в пространстве особенности. Некоторые особенности могут не иметь совпадений, например, они могут быть частью фона или на некоторых изображениях оказаться невидимыми из-за сложного рельефа поверхности объекта. Выбор порога позволяет сократить число ложных срабатываний [1]. В идеале порог должен адаптироваться к различным регионам пространства особенности. При наличии достаточного количества тестовых данных иногда воз- можно определить влияние величины порога для всевозможных особенностей [2].

Но чаще всего берется произвольный набор изображений для сравнения при построении панорамы или реконструкции 3D-моделей. В этом случае полезным может быть сравнение расстояний между ближайшими соседними особенностями, взятыми с другого изображения (см. рис. 7).

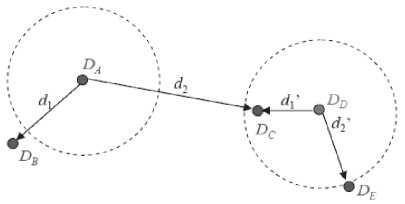
Рис. 7. Расстояние между соседними особенностями

Это расстояние можно определить как отношение расстояния между ближайшими соседними особенностями (NNDR – Nearest Neighbor Distance Ratio):

NNDR = d^-d2

VPlFI \D, - Del

где d₁ и d₂ – расстояния до ближайших особенностей, D_A – целевой дескриптор, D_B и D_C – ближайшие соседние дескрипторы.

Реализация алгоритмов сравнения

После выбора стратегии сравнения необходимо выбрать способ эффективного поиска кандидатов на сравнение. Самый простой способ установить соответствия между особенными точками состоит в том, что все особенности одного изображения сравниваются со всеми особенностями других изображений. Этот метод известен как метод полного перебора, или метод «грубой силы» (Brute force). Для каждого дескриптора первого изображения ищется наиболее близкий дескриптор из набора дескрипторов второго изображения. Если принять количество дескрипторов в первом наборе за N , во втором M , то количество операций сравнения N × M . При среднем количестве дескрипторов в наборе более 500 количество сравнений превысит 250^.10³. Наиболее оптимальную пару дескрипторов определяют с помощью порога. Существует несколько модификаций метода полного перебора, отличающихся способами вычисления расстояний между соседними дескрипторами, например, с помощью расстояния Хамминга (BruteForce-Hamming). Большое число сравнений обусловливают и низкую производительность данного алгоритма, но обеспечивают приемлемую точность.

Более оптимальный подход предполагает использование индексирующей структуры, такой как многомерное дерево поиска или хеш-таблицы, для быстрого поиска соседей особенности. Такие структуры могут поддерживаться для каждого изображения независимо (это может помочь в ситуациях, когда необходимо только оценить потенциал соответствия, например для поиска определенного объекта) или глобально, поместив все изображения в индексированную базу данных; это устранит потребность в выполнении итераций по каждому изображению.

Самый простой метод для реализации – многомерное хеширование, которое отображает дескрипторы в блоки фиксированного размера, основанные на некоторой функции, применяемой к каждому дескриптору. Во время сравнения каждый новый признак хешируется в блок и поиск соседних блоков используется для возврата потенциальных кандидатов на сравнение, которые затем могут быть отсортированы или градуированы для определения допустимых соответствий. Пример простого хеширования – вейвлеты Хаара [5]. При построении сравнивающей структуры каждый регион размера 8×8 пикселей, ориентированный и нормализованный, конвертируется в дескриптор особенности путем суммирования разных квадрантов региона. В результате значения дескриптора нормализуются по их стандартным отклонениям и формируется одномерный массив. Трехмерные индексы формируются путем объединения трех квантованных значений для индексации 23 = 8 массивов, в которых хранятся дескрипторы особенности. При запросах к структуре выбирается только ближайший (главный) индекс. Остальные измерения индекса используются для выбора k-ближайших (k-nearest) элементов.

Более сложная, но широко применяемая версия хеширования называется окрестночувствительным хешированием, которое объединяет независимо вычисленные хешфункции для индексации особенностей [5].

Другим широко используемым классом индексирующих структур являются многомерные деревья поиска. Самыми известными из них являются KD-деревья. Это бинарные деревья ограничивающих параллелепипедов, вложенных друг в друга. Каждый параллелепипед в KD-дереве разбивается плоскостью, перпендикулярной одной из осей координат, на два дочерних параллелепипеда. Для максимизации некоторого критерия, такого как баланс дерева поиска, устанавливается порог вдоль каждой оси. KD-деревья часто используются в алгоритмах отсечения невидимых плоскостей в компьютерной графике. Существует достаточное количество библиотек с открытым исходным кодом, реализующих основные операции с KD-деревьями (например ANN – Approximate Nearest Neighbor, а также модуль FLANN – Fast Library for Approximate Nearest Neighbors, входящий в состав библиотеки OpenCV).

Предлагаемый алгоритм сравнения

Характерной чертой рассмотренных алгоритмов сравнения является равнозначный выбор особенных точек для сравнения. Это значит, что дескриптор особенности первого изображения сравнивается со всеми дескрипторами особенностей второго изображения. Это может приводить к неверным соответствиям при сравнении, например из-за значительных изменений в положении объекта, изменении освещения или других причин. В дальнейшем при обработке результатов сравнения такие выбросы отсеиваются.

Предлагаемый алгоритм сравнения не просто отбрасывает особенные точки, имеющие ложное соответствие, а ищет для них наиболее подходя- щие соответствия, при этом не добавляя новых ложных соответствий.

Весь алгоритм можно разбить на несколько этапов:

• -    выделение особенных точек с помощью общедоступных реализаций алгоритмов – SIFT, SURF (Speeded-Up Robust Features) и подобных. Вычисление дескрипторов и установление первоначальных соответствий между точками;

• -    из всех соответствий, найденных на первом этапе, оставить только устойчивые;

• -    вокруг каждой особенности, оставленной на втором этапе, выделяется область, являющаяся окружностью. Области выделяются парами на первом и втором изображениях. Радиус окружности выбирается произвольно. Эта величина достаточно условная и может зависеть, например, от количества особенностей, оставленных на первом этапе, или подбираться экспериментально для каждого набора изображений (обычно 32 ... 128 пикселей). На рис. 8 показаны строгие соответствия и выделены некоторые области. Выделенные области ограничивают регион поиска соответствий для тех особенностей, которые оказались внутри области;

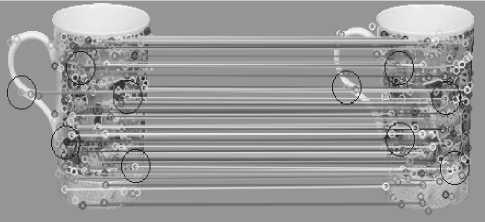
Рис. 8. Устойчивые соответствия с выделенными областями

- в каждой области выбираются особенности, назовем их вторичные, не имеющие соответствий или отброшенные на втором этапе. Поиск соответствий для вторичных особенностей производится только в парных областях (см. рис. 9). Пороговое значение для расстояния между вторичными особенностями либо не изменяется, либо повышается. Процент повышения можно подобрать экспериментально, но не более 1015%, чтобы предупредить появление ложных соответствий.

Третий и четвертый по счету этапы можно повторять итерационно для повышения количества надежных соответствий. Такой алгоритм, работающий с небольшими участками изображений, позволяет найти истин- ные соответствия между точками даже в тех случаях, когда их не удается обнаружить с помощью эпиполярного ограничения. Например, в тех случаях, когда объект на каком-либо изображении смещается относительно центра камеры или объект имеет сложную геометрическую форму и особенные точки перемещаются на разные расстояния. На рис. 10 представлен результат работы одной итерации алгоритма. Сравнив его с рис. 5, можно заметить, что количество истинных соответствий значительно увеличилось, а ложные соответствия отсутствуют.

Рис. 9. Сравнение вторичных особенностей

Рис. 10. Результат работы алгоритма

На рис. 10 также видны особые точки, для которых не нашлось соответствий. В таком случае можно выполнять несколько итераций, на каждом шаге повышая порог, но в таком случае гарантировать приемлемое качество работы алгоритма будет трудно.

Экспериментальные исследования

Для проверки работоспособности и точности предлагаемого алгоритма были выполнены экспериментальные исследования. В ходе эксперимента вычислялись количественные характеристики как предлагаемого алгоритма сравнения, так и нескольких других известных алгоритмов, описанных выше. Для получения изображений тестовых объектов используется установка, показанная на рис. 11. Данная установка использует поворотный стол для получения изображений объекта с разных ракурсов.

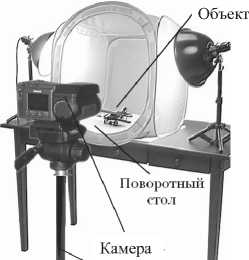
Рис. 11. Экспериментальная установка

На рис. 12 представлены три набора тестовых изображений с разной текстурой. Каждый набор содержит по 4 изображения, полученных регистрацией объектов, повернутых вокруг вертикальной оси на 0; 5°; 10° и 20° соответственно. В наборе присутствуют как изображения с легко локализуемыми особенностями, так и со сплошной текстурой, что может затруднить поиск и выделение особенностей. Поиск и сравнение особенных точек производился по парным изображениям – первое изображение из набора последовательно сравнивалось с остальными изображениями набора (вторым, третьим и четвертым).

Для повышения чистоты эксперимента поиск особенностей на изображениях выполнялся с помощью нескольких алгоритмов, что позволило снизить влияние их внутренней реализации на устойчивость алгоритмов сравнения. В основном такое влияние оказывают выбранные способы представления и хранения переменных в памяти [1]. В качестве алгоритмов поиска особенностей использовались общедоступные реализации алгоритмов SIFT[3], MSER[4] и SURF [4]. Эти алгоритмы объединяет то, что их дескрипторы представлены числами с «плавающей» запятой (float) и хранятся в виде вектора.

В качестве традиционных алгоритмов сравнения были выбраны:

• -    BruteForce (BF) – алгоритм поиска, основанный на полном переборе всех доступных вариантов («грубой силы»);

• -    FlannBasedMatcher (FBM) – алгоритм сравнения, основанный на KD-деревьях;

• -    VectorMatcher (VM) – алгоритм сравнения дескрипторов, представленных векторами в конечном пространстве.

Рассмотрим методику проведения эксперимента. Эксперимент состоит из циклов, а цикл из нескольких этапов:

• -    формирование пары – алгоритм обнаружения особых точек, алгоритм сравнения;

• -    поиск особых точек на каждом изображении;

• -    вычисление дескрипторов особых точек;

• -    нахождение соответствий между дескрипторами;

• -    фильтрация установленных соответствий с помощью порогового значения;

• -    вычисление количественных характеристик алгоритма сравнения.

В каждом цикле перечисленные этапы последовательно выполнялись для каждой пары алгоритмов – поиска особых точек и их сравнения с пороговым значением 0,25. Порог устанавливался непосредственно перед каждым циклом. При вычислении результирующих характеристик алгоритмов сравнения брались средние значения, вычисленные для алгоритма в одном цикле. Полученные в ходе экспериментальных циклов данные сведены в таблицы 1-6.

Рис. 12. Тестовый набор изображений

Таблица 1. Среднее число особенностей

№ набора изображений	SIFT	MSER	SURF
1	178	15	129
2	145	23	141
3	140	20	86

Таблица 2. Алгоритм BruteForce

№ набора изображений	BF SIFT	BF MSER	BF SURF	Среднее значение
1	43	3	51	45
2	44	14	80	58
3	20	8	34	34

В таблице 1 представлено число найденных особенностей, усредненное по количеству изображений в наборе. По значениям в этой таблице можно косвенно оценить текстуру тестовых объектов на изображениях.

Таблица 3. Алгоритм FlannBasedMatcher

№ набора изображений	FBM SIFT	FBM MSER	FBM SURF	Среднее значение
1	43	3	51	45
2	44	14	80	58
3	20	8	34	34

Таблица 4. Алгоритм VectorMatcher

№ набора изображений	VM SIFT	VM MSER	VM SURF	Среднее значение
1	74	5	79	52
2	66	20	109	65
3	50	11	58	40

Таблица 5. Предлагаемый алгоритм

№ набора изображений	* SIFT	* MSER	* SURF	Среднее значение
1	37	4	42	28
2	35	9	57	34
3	18	6	19	15

Циклы эксперимента представлены в таблицах 2-5 (порог 0,25). Каждый цикл запускался несколько раз. Среднее значение в таблицах учи- тывают как истинные, так и ложные найденные соответствия.

Таблица 6. Сводная таблица характеристик

Величина	BF	FBM	VM	*
TP	37	35	36	35
FN	5	7	10	1
FP	8	10	16	1
TN	62	66	67	60
TPR	0,88	0,83	0,70	0,95
FPR	0,11	0,3	0,21	0,02

В таблице 6 представлены количественные характеристики работы алгоритмов сравнения, полученные как средние значения по всем трем наборам значений. Предлагаемый алгоритм (обозначенный символом «звездочка») при прочих равных условиях показал высокий процент найденных истинных соответствий. Одновременно эксперимент показал, что количество истинных соответствий, устанавливаемых алгоритмом, необходимо увеличивать, например, с помощью динамического порога.

Выводы

Выполненные исследования позволяют оценить различные алгоритмы выделения и сравнения точечных особенностей на наборах изображений с точки зрения устойчивости к различным преобразованиям. Авторами предложен алгоритм сравнения особенностей, реализованный с помощью библиотеки OpenCV, повышающий количество истинных соответствий и их качество. Данный алгоритм также пригоден для последующей адаптации к другим задачам компьютерного зрения. Например, фундаментальная матрица обычно вычисляется на основе семи строгих соответствий, вычисляемых для всего изображения.

Затем эпиполярное ограничение, закодированное в фундаментальной матрице, используется для уточнения вычисления соответствий. Чем сложнее объект, тем сложнее будет обнаружить соответствия с помощью эпиполей. В таких случаях фундаментальную матрицу можно строить по семи соответствиям, найденным в выделенных областях (см. рис. 8). При таких небольших размерах участка изображения точности фундаментальной матрицы будет вполне достаточно для получения из нее методом разложения (SVD) матрицы проекции, которая в дальнейшем используется в алгоритме триангуляции для получения трехмерных координат точек.