Выявление характерного времени процесса в динамике солнечной активности

Исследование космической погоды и ее проявлений продолжается более века. Выявлено, что динамика всех биологических процессов зависит от космических ритмов. Влияние космической погоды на среду обитания реализуется через несколько каналов. Наиболее значимым из них являются электромагнитные поля и радиоволны, генерируемые различными источниками, которые регулируются солнечной активностью.

Многие явления связаны с активной областью на Солнце: пятна, факелы, факельные поля, сильные магнитные поля, коро-нальные конденсации, усиленное радиоиз- лучение, источники ультрафиолетового и рентгеновского излучения, области вспышек. Некоторые области более активны, чем другие, но не существует единственного признака, по которому можно было бы охарактеризовать активную область на Солнце. Основными признаками активности являются площади пятен, количество пятен, размеры и интенсивности факелов и факельных полей, потоки рентгеновского, ультрафиолетового и радиоизлучения.

Количество пятен на Солнце или Числа Вольфа W рассчитываются по следующей формуле [0] :

w = k(f + 10 g),

где f - количество наблюдаемых пятен;

g - количество наблюдаемых групп пятен; к - нормировочный коэффициент.

В любой динамической системе явления проявляются значительнее в зависимости от уровня, на котором данные рассматриваются. При анализе исходных данных трудно определить характерное время, хотя во многих случаях присутствует скрытая закономерность. Поэтому применяются различные методы и преобразования для поиска периодических компонент процесса, которые и будут рассмотрены далее.

На рисунке 1 изображена ежедневная динамика чисел Вольфа за один цикл Швабе-Вольфа на временном интервале 1996-2010 гг. [0]. Цикл Швабе-Вольфа – это ярко выраженный цикл солнечной активности, который в среднем равен 11 годам. «Одиннадцатилетним» цикл называют условно, в XVIII-XX веках его длина менялась от 7 до 17 лет, а в XX веке в среднем была ближе к 10.5 годам.

1996     1998     2000     2002     2004     2006     2008     2010

t, ДНИ

Рис. 1. Динамика чисел Вольфа за один цикл

Для определения периодических компонент нелинейных процессов с трендом требуется провести исключение тренда так, чтобы был получен ряд, гарантированно содержащий близкие к периодам величины.

По структуре ряды экспериментальных данных представляют собой либо колебания относительно постоянного уровня, либо композицию характеристик процесса, имеющих принципиально разные масштабы изменения аргумента. При этом «медленные» движения маскируют характеристики «быстрых» движений.

Характеристики тренда кодируются через опорные точки. Задача состоит в том, чтобы найти положение этих точек, которое обеспечит исключение трендовой составляющей ряда. Простейший случай, когда для решения используются всего три точки y_t-Δt, y_t и y_t+Δt, расположенные на равном расстоянии друг от друга. В такой постановке задача сводится к классическим результатам теории пропорций, в соответствии с которыми происходит разбиение отрезка [0] .

Преобразование эмпирических данных приводит к исключению трендовых участков из данных по следующей формуле:

P(t, Δt) = ln(

y t-Δt ⋅ y t+Δt ^y t²

).

Возьмем фиксированный шаг Δt и исключим тренд из данных ежедневной динамики солнечной активности. Результат исключения тренда для Δt = 10 представлен на рисунке 2.

Рис. 2. Временной ряд без тренда

Если абсолютная величина математического ожидания равна нулю, то реализовывается идеальное исключение тренда. В реальности математическое ожидание отличается от нуля, поэтому вычислим модуль математического ожидания полученного временного ряда. Такую операцию проделываем для последовательности Δt разной длительности. Для анализа рекомендуется брать не более 2/3n точек, так как на маленьком интервале в конце растет ошибка. Δt, для которого модуль математического ожидания имеет минимальное значение, будет наилучшим вариантом исключения тренда. Это значение будет соответствовать почти-периоду, характерному для данного процесса, который наиболее близок к истинному периоду системы [0]. Построим зависимость модуля математического ожидания от Δt для данных рисунка 1. Результат представлен на рисунке 3.

Рис. 3. Модуль математического ожидания

Глобальный минимум равен 26 дням, что соответствует синодическому периоду обращения Солнца на экваторе. Это про- межуток времени, спустя который для наблюдателя с Земли часть поверхности Солнца повторит свое положение.

Еще одним способом выявления почти- функция или функция Альтера-Джонсона: периоды системы является сдвиговая п-т

а(т) = — У |f(t + т) - f(t)|, n — тд—I t=1

где n - общее число отсчетов функции f(t); f(t) - периодическая функция;

т - период функции.

В основе данного подхода лежит фундаментальное характеристическое свойство периода функции, которое состоит в том, что значения функции повторяются через интервал изменения переменной равный периоду. Положение локальных минимумов сдвиговой функции указывает на наличие в исходном временном ряду почти-периодов различных длительностей.

Предварительно исключив тренд с помощью преобразования, рассмотренного ранее, построим сдвиговую функцию для динамики чисел Вольфа за один цикл ежедневных данных для разных сдвижек исключения тренда At. Результат представлен на рисунке 4.

Рис. 4. Сдвиговая функция для ежедневных данных

На рисунке 4 выделяется один глобальный экстремум, который соответствует 27 дням, что в точности равно осевому вращению Солнца. Данный цикл проявляется во многих сферах деятельности, например, российский врач М.В. Соколов и известный шведский ученый С. Аррениус нашли тенденцию к 27-дневной повторяемости в эпилептических припадках. Швейцарский врач К. Киндлиман обнаружил на много- летней статистике около 27-дневный период смертности от сердечно-сосудистых заболеваний: показатель смертности возрастает в дни, когда большие пятна пересекают центральный солнечный меридиан [0].

Динамику солнечной активности за один 11 -летний цикл можно описать моделью ограниченного роста, а именно моделью Гомперца:

dy где – ежедневная динамика;

dy

~Г = Ae dt

kty,

у - кумулятивная сумма исходных данных;

t – дни;

А и k – параметры модели.

Для поиска параметров модели воспользуемся методом анаморфоз. Анаморфоза – это нелинейное преобразование, которое приводит данные в линейную зависимость [0] .

Анаморфоза модели Гомперца:

dy у dt

= Ae~kt.

Взяв натуральный логарифм, получим анаморфозу:

ЧУ)=

ln(A) — kt.

Спрямление данных, которые соответствуют модели Гомперца, дает их построение в координатах:

чун

Построим данные динамики чисел Вольфа за один цикл в координатах. Результат изображен на рисунке 5.

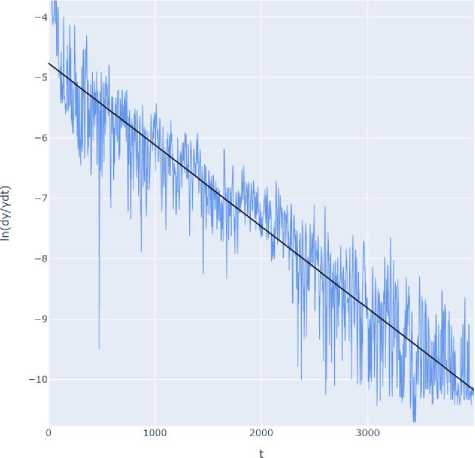
Рис. 5. Анаморфоза кривой модели Гомперца

Тангенс угла наклона прямой определяет параметр модели k и равен 0.00139. Характерное время процесса равно 719 дней. Это время, за которое количество чисел

Вольфа изменится в e раз. Для других циклов солнечной активности характерное время колеблется от 600 до 833 дней и в среднем составляет 679 дней (1.86 года).

Проблеме цикличности развития в связи с процессами в Солнечной системе посвящено большое количество исследований. В результате анализа был выявлен один из циклов, который часто встречается в раз- личных областях науки. Изменяя детализацию данных и шага сдвиговой функции, можно найти и другие значимые периоды, которые будут представлены в следующих исследованиях.