Вырожденные интегро-дифференциальные уравнения специального вида в банаховых пространствах и их приложения
Автор: Фалалеев Михаил Валентинович, Орлов Сергей Сергеевич
Статья в выпуске: 4 (221), 2011 года.
Бесплатный доступ
В статье методами теории фундаментальных оператор-функций сингулярных интегро-дифференциальных операторов исследован специальный класс вырожденных линейных интегро-дифференциальных уравнений в банаховых пространствах, для которого получены достаточные условия существования и единственности классического решения задачи Коши. Абстрактные результаты проиллюстрированы на примере двух начально-краевых задач, возникающих в математической теории вязко-упругости.
Банаховы пространства, распределения, фундаментальная оператор-функция
Короткий адрес: https://sciup.org/147159119
IDR: 147159119
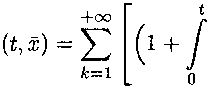
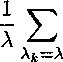
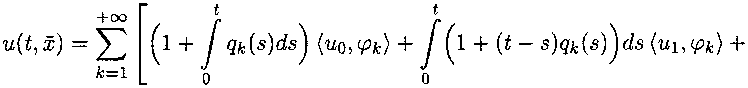
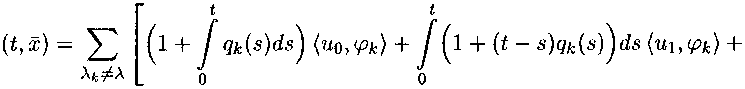
Список литературы Вырожденные интегро-дифференциальные уравнения специального вида в банаховых пространствах и их приложения
- Фалалеев, М.В. Начально-краевые задачи для интегро-дифференциальных уравнений вязкоупругости/М.В. Фалалеев, С.С. Орлов//Обозрение прикладной и промышленной математики. -2010. -Т. 17, вып. 4. -С. 597 -600.
- Sviridyuk, G.A. Linear Sobolev Type Equations and Degenerate Semigroups of Operators/G.A. Sviridyuk, V.E. Fedorov. -Utrecht; Boston; Köln; Tokyo: VSP, 2003.
- Свиридюк, Г.А. К общей теории полугрупп операторов/Г.А. Свиридюк//Успехи мат. наук. -1994. -Т. 49, № 4. -С. 47 -74.
- Lyapunov-Schmidt Methods in Nonlinear Analysis and Applications/N. Sidorov, B. Loginov, A. Sinitsyn and M. Falaleev. -Dordrecht: Kluwer Acad. Publ., 2002.
- Фалалеев, М.В. Фундаментальные оператор-функции сингулярных дифференциальных операторов в условиях спектральной ограниченности/М.В. Фалалеев, Е.Ю. Граждан-цева//Дифференц. уравнения -2006. -Т. 42, № 6. -С. 769 -774.
- Фалалеев, М.В. Фундаментальные оператор-функции сингулярных дифференциальных операторов в условиях секториальности и радиальности/М.В. Фалалеев//Известия вузов. Математика. -2006. -№ 10. -С. 68 -75.
- Cavalcanti, М.М. Existence and Uniform Decay for a Non-Linear Viscoelastic Equation with Strong Damping/M.M. Cavalcanti, V.N. Domingos Cavalcanti, J. Ferreira//Math. Meth. Appl. Sei. -2001. -V. 24. -P. 1043 -1053.
- Замышляева, A.A. Фазовые пространства одного класса линейных уравнений Соболевского типа второго порядка/A.A. Замышляева//Вычислит. технологии. -2003. -Т. 8, № 4. -С. 45 -54.
Статья научная
