Вырожденные потоки разрешающих операторов для нестационарных уравнений соболевского типа

Пусть X , Y - банаховы пространства. Оператор L е L ( X ; Y ) (т.е. линейный непрерывный) и оператор M е Cl ( X ; Y ) (т.е. линейный замкнутый, плотно определенный в X ). На промежутке J с R рассмотрим задачу Коши

X ( 1 0 ) = x 0 (1) при t 0 е J для нестационарного уравнения вида

• LX = aMx + g , (2) где ker L Ф {0}, а скалярная функция a : J ^ R ₊ и вектор-функция g : J ^ Y подлежат дальнейшему определению.

При условии a = const уравнение (2) в силу нетривиальности ядра оператора L относится к стационарным уравнениям соболевского типа [1]. В настоящее время уравнения соболевского типа активно исследуются в различных направлениях, о чем могут свидетельствовать монографии, целиком или частично посвященные их исследованию [1–7]. Результаты этих исследований стали основой для изучения систем леонтьевского типа (см. напр. [8, 9]), задач оптимального управления (см. напр. [5]), на основе которых было предложено задачу восстановления динамически искаженного сигнала [10, 11] рассматривать как задачу оптимального измерения [12, 13]. Более того, стационарные уравнения соболевского типа начали рассматриваться в квазибанаховых пространствах [14–16], а также в пространствах «шумов» [17, 18]. Отметим, также, что основой исследования уравнений соболевского типа стал метод фазового пространства [6, 19].

Нестационарные уравнения соболевского типа исследовались автором довольно фрагментарно (см. напр. [20]). Целью данной работы является полное математическое обоснование методов, необходимых при нахождении решении нестационарных уравнений соболевского типа вида (2) и начальных задач для него.

Статья кроме введения, заключения и списка литературы содержит три части. В первой весьма кратко описывается теория относительно p -ограниченных операторов. Все результаты данной части приведены без доказательства, обосновывается лишь переход от контурного интегрирования к предельным переходам. Далее, во второй (основной) части рассматриваются вырожденные группы и потоки операторов, используя которые в третьей части получены решения начальных задач для нестационарных уравнений соболевского типа. Список литературы не претендует на полноту и отражает лишь вкусы и пристрастия автора.

Автор считает своим приятным долгом выразить искреннюю благодарность своему научному консультанту профессору А.Л. Шестакову за внимание к данной работе, профессору Г.А. Свиридюку за строгую, но конструктивную критику, а также коллектив кафедры уравнений математической физики за плодотворные дискуссии и интерес, проявленный к данной работе.

Относительно p -ограниченные операторы

Следуя [1], множества p ( M ) = { pе C :( p L - M ) ^{- 1} е L ( Y ; X )} и О ( M ) = C \ p ^L ( M ) назовем L - резольвентным множеством и L - спектром оператора M соответственно. В силу результатов [1] множество p ^L ( M ) является открытым, а поэтому o ^L ( M ) всегда замкнут.

L -резольвентное множество оператора M может быть пустым множеством, например, если ker L n ker M Ф {0}. Предполагая, что множество p ^L ( M ) не пусто, введем в рассмотрение опера-тор-функции комплексного переменного ( p L - M ) ^{- 1}, R p ( M ) = ( p L - M ) ^{- 1} L и

L p ( M ) = L( p L - M ) ¹ с областью определения p ^L ( M ), которые будем называть соответственно L - резольвентой, правой и левой L-резольвентами оператора M . В силу [1], L -резольвента, правая и левая L -резольвенты оператора M голоморфны в p ^L ( M ).

Определение 1. Оператор M назовем спектрально ограниченным относительно оператора L (коротко, ( L , о ) - ограниченным ), если Я r е R + V p е C (| p | > r ) ^ ( ре p ( M )).

Возьмем ( L, о )-ограниченный оператор M , выберем в комплексной плоскости C контур

Y= { pе С :| p | = h >  r }. Тогда имеют смысл такие интегралы, как интегралы от голоморфных опе-ратор-функций комплексного переменного по замкнутому контуру,

P =    Р< ( M ) d p ,    Q =   j L p ( м ) d p .                    (3)

i n i *                    2 П *

γγ

Так как правая R p ( M ) = ( p L - M ) ^{- 1} L и левая L p ( M ) = L( p L - M ) ^{- 1} L -резольвенты оператора

M голоморфны [1], то операторы P и Q не зависят от радиуса h контура у •

Лемма 1. [1] Пусть L е L ( X ; Y ) , M е Cl ( X ; Y ) и оператор M ( L , о ) -ограничен. Тогда операторы P е L ( X ) и Q е L ( Y ) являются проекторами.

Введем обозначение X ⁰ = ker P , X ¹ = imP , Y ⁰ = ker Q , Y ¹ = imQ ; а через L k ( M k ) обозначим сужение оператора L ( M ) на X^k ( X^k n domM ), k = 0,1.

Теорема 1 (теорема Г.А. Свиридюка о расщеплении). [1] Пусть операторы L е L ( X ; Y ) и M е Cl ( X ; Y ) , причем оператор M ( L , о ) -ограничен. Тогда

• (i)    операторы L k е L ( X k ; Y^k ) и M k е Cl ( X k ; Y^k ) , k = 0,1 ;

• (ii)    существуют операторы L - е L (Y 1 ; X 1 ) и M ₀ ¹ е L (Y ⁰; X ⁰).

При условии ( L , о ) -ограниченности оператора M , согласно теореме 1, существуют операторы H = M - ¹ L ₀ е L ( X ⁰) и 5 = L - ¹ M 1 е L ( X 1 ), используя которые можно разложить L -резольвенту оператора M в кольце Щ >  r в ряд Лорана

∞∞

( p L - M ) ^{- 1} =- ^ pH^kM 01 ( I y - Q ) + ^ p- ^kS^{k - 1} L - ¹ Q .

k = 1                             k = 0

При этом бесконечно удаленная точка является

• (i)    устранимой особой точкой , если H = O ;

• (ii)    полюсом порядка p е N , если H^p Ф O , а H^{p + 1} = O ;

• (iii)    существенно особой точкой , если H^k Ф O для всех k е N .

Бесконечно удаленную точку будем называть полюсом порядка p е N ₀ ( = {0} и N ), если она является устранимой особой точкой ( p = 0) или полюсом порядка p е N .

Определение 2. Оператор M будем называть ( L , p ) - ограниченным ( p е N ₀), если он ( L , о ) -ограничен и бесконечность является полюсом порядка p е N ₀ для ( p L - M ) ^{- 1}.

Следствие 1. Пусть оператор M ( L , p ) - ограничен ( p е N ₀) . Тогда

P = lim Д Д ( M )) p ^{+ 1},     Q = lim Д М ( M )) ^{p +} 1 .

д ^^                   д^^

Доказательство. Рассмотрим

P = lim ( m R M ( M ) ) p ^{+ 1} = lim ( д ( m L - M ) ¹ L ( P + ( I X - P д^^   ^M        д^^

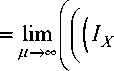
- —L ^{- 1} M, Д ¹

,-17 ^{p +1}       ,                     , p + + 1

) J P + (д(mH -Ix у1H)  (Ix -P)

= P + O ( I x - P ) = P .

Утверждение относительно проектора Q доказывается аналогично. Следствие доказано.

Вырожденные группы и потоки операторов.

Пусть X , Y - банаховы пространства, операторы L е L ( X ; Y ) и M е Cl ( X ; Y ).

Определение 3. Однопараметрическое семейство X ( • ): R ^ L ( X ) будем называть вырожденной группой операторов , если выполнены условия

• (i)    X (0) = P ,

• (ii)    X ( t ) X ( s ) = X ( t + s ) для всех t , s е R .

Замечание 1. Если первое условие определения 3 заменить на X (0) = I_X , то группа вырожденной не является, и в этом случае ее называют просто группой операторов.

Вырожденная группа операторов называется аналитической , если она допускает аналитическое продолжение во всю комплексную плоскость с сохранением свойств (i) и (ii).

Теорема 3. [1] Пусть оператор M (L,^) -ограничен. Тогда существует аналитическая группа {X(t)е L(X): tе R} ({Y(t)еL(Y): tе R}), причем ее операторы задаются интегралами типа Данфорда-Тейлора по контуру у= {де С :|Д = h > r}

X ( t ) =     J К Д ( M ) eYu.   Y ( t ) =     |T ( M ) e Pm .

2m^j                      2 n i^J

Y

V           y             7

Замечание 2. Сужение операторов X ( t )| _х = exp( tS ), где S = L 1 ¹ M 1 е L ( X 1 ) из теоремы 1.

Следствие 2. Пусть оператор M ( L , p )- ограничен ( p е N ₀) . Тогда операторы группы

{ X ( t ) е L ( X ): t е R } ( { Y ( t ) е L (Y ): t е R } ) заданы аппроксимациями Хилле-Уиддера-Поста

X (t) = lim k -^^

и     I ^k

|r L ( M )

V t         7

Y ( t ) = lim k >■

V

(,, JkJ

^^L ! ^{( M} )

V t 7 7

Доказательство. Рассмотрим группу { X ( t ) е L ( X ): t е R } . В силу теоремы 2 и следствия 1

X (t) = lim k ^^

( kRL (M) (P + ( Ix - P))

V t t

k

= lim k ^^

V

k ( k

L — Mi t V t ^{1        1}

1 k( k

Li P + k ( ^^ L o

7-1              J k

^{- M} 0 7 ^L 0 ⁽ I X ^{- P} )

(,

= lim (Ix k ^~ VX

V

- kL-1 Mx t 1 1

P +

- 1

k ( k и i I

71 tH ^- I^х J

V

J ^k

H

( I x - P ) = exp( St ) P + O ( I x 7

- P ).

Откуда, принимая во внимание замечание 2, получаем утверждение относительно X ( t ).

Утверждение относительно группы Y ( t ) доказывается аналогично. Следствие доказано.

Определение 4. Двухпараметрическое семейство X ( • , • ): R х R ^ L ( X ) будем называть вырожденным потоком операторов , если выполнены условия

• (i)    X ( t , t ) = P , для всех t е R

• (ii)    X ( t, T ) X ( t , s ) = X ( t , s ) для всех t, T ,s е R .

Замечание 3. Если первое условие определения 4 заменить на X(t, t) = IX, то поток вырож денным не является, и в этом случае его называют просто потоком операторов.

Вырожденный поток операторов называется аналитическим , если он допускает аналитическое продолжение во всю комплексную плоскость с сохранением свойств (i) и (ii).

Пусть оператор M (L, p) -ограничен (p е N0) и функция a е C(R;R). По аналогии с (4) рас смотрим при t, 5 е R выражение

г

t

к

X ( t , 5 )

₁                                      ',

= — pR ( M )exp A a ( Z ) d Z d R , 2m- " ^J

Y

k 5

где контур у = { ц е С :| ц\= h >  r }.

Теорема 4. Пусть оператор M (L, p) -ограничен (p е N0) и функция a е C(R;R). Тогда се мейство { X(t, 5) е L (X): t, 5 е R}, операторы которого заданы формулой (5), является вырожденным аналитическим потоком операторов.

Доказательство. Для операторов (5) потока {X(t, 5) е L (X): t, 5 е R} очевидно существует аналитическое продолжение.

Покажем, что X(t, 5) образуют поток операторов. Свойство (i) из определения 4 следует из способа задания операторов X(t, 5). Рассмотрим свойство (ii) из определения 4:

X ( t , т ) X ( т , 5 ) =

= 1

( 2 n i ) ²

( 2 n i ) ²

( t k

J R R ⁽ M )ехр r J a ^{( Z} ) d ^Z d R- J ^r1 L ⁽ M )exp 1 J a ^{( Z} ) d ^Z d i =

( т A

у

k T 7 у( T k k

k5         7( t k

J J R R ⁽ M ) R i ⁽ M ^)exP ^ J a ^{( Z} ) ^{d Z d i ex}P a J a^{( Z} ) ^{d Z d} A =

у k Y’

k 5

( 2 n i ) ²

JJ

(T            I iJa(Z)dZ di

5         7

i - Ц

⁷ 7

( t

k т 7k

R R ( M )exp Ц a ( Z ) d Z d ц + k T 7

k

( T

+ J R i ( M )exp i J a( Z ) d Z J

( t I k expl ц J a(Z)dZ IdR

Y            k 5        7 у

т____

Ц - i

k

di

где точка ц е у лежит внутри области, ограниченной контуром у1, а точка iе у1 находится вне области, ограниченной контуром у. Тогда в силу теоремы о вычетах, учитывая последнее выра- жение, получим

X ( t , T ) X ( T , 5 ) = —

( 2 n i )

( t k

( T k

J R L ⁽ M ^)exp Ц J a^{( Z} ) ^{d Z d} R • J ^R i l ⁽ M ^)exp ⁱ J a^{( Z} ) ^{d Z d i} =

у

k T 7 у

k5         7

1                  ( (t-             T kk

= VT f R L ⁽ M ^)exp Ц J a ^{( Z} ) ^{d Z +} J a ^{( Z} ) ^{d Z d} R = ^{X (} t , ⁵ ).

2 nz^J,                    i ^j

у

k

k T              5

Теорема доказана.

Замечание 4. В силу теоремы 1 сужение операторов потока X ( t , 5 )| X

= exp ( S J t a ( Z ) d Z )

, где

оператор S = L - ¹ M ₁ е L ( X ¹).

Замечание 5. В пространстве L ( У ) по аналогии с (5) также можно задать поток операторов следующей формулой

У ( t , 5 ) = 2~г J L L ( M )exp ( Ц J a( Z ) d Z ) d R .                       (6)

Доказательство свойств такого потока аналогично доказательству теоремы 4.

Следствие 3. Пусть оператор M ( L , p ) -ограничен ( p е N ₀) и функция a е C ( R ; R ₊ ) . Тогда операторы потоков { X ( t , s ) е L ( X ): t , s е R } и { У ( t , s ) е L ( У ): t , s е R } задаются с помощью ап-

проксимаций Хилле–Уиддера–Поста ff           t         А - 1 А k X ( t ) = lim L - 1 M\a( Z ) d ( L и k ^~      k V V          s          7 7

f f            t           А - 1 А k У ( t ) = lim L L - 1 M\a( Z )d (     .     (7) k ^~        k J V V          s          7 7

Начальные задачи для нестационарных уравнений соболевского типа.

Пусть X, У - банаховы пространства, операторы L е L (X; У) и M е Cl (X; У). Рассмотрим задачу Коши x (10) = x 0                                               (8)

для однородного нестационарного уравнения вида

Lx = aMx ,                                     (9)

где функция a : R ^ R ₊ подлежит дальнейшему определению.

Определение 5. Вектор-функция x е C 1 ( R ; X ) называется ( классическим ) решением (9), если подстановка этой вектор-функции в уравнение (9) делает его верным тожеством. Решение x = x ( t ) уравнения (9) будем называть решением задачи Коши (8) для уравнения (9) (коротко, задачи (8), (9)), если оно удовлетворяет условию Коши (3) при некотором x ₀ е X .

Замкнутое множество pc X назовем фазовым пространством уравнения (9), если

• (i)    любое решение x = x ( t ) лежит в р поточечно (т.е. x ( t ) ер при всех t е R ),

• (ii)    при любом x ₀ ер существует единственное решение задачи Коши (8), (9).

Вместе с уравнением (9) будем рассматривать эквивалентное ему при v е p^L ( M ) уравнение

L ( v L - M ) ^{- 1} y = aM ( v L - M ) ^{- 1} y .                          (10)

Теорема 5. Пусть оператор M ( L , p ) -ограничен ( p е N ₀) и функция a е C ( R ; R ₊ ) . Тогда фазовым пространством уравнения (9) ((10)) является множество X ¹ ( У 1 ) .

Доказательство. В силу теоремы 1 уравнение (9) эквивалентно системе Hx° = ax ⁰,        x ¹ = Sx ¹.

Выразим x ⁰ из первого уравнения этой системы и получим x ⁰ = ^Hx⁰ . Продифференцируем это выражение и применим оператор ^И , в силу уравнения получим

• ¹    Hx ⁰ = ¹ Hd ^f1 Hx ⁰ ) = И 2 ¹ d ^f1 x ⁰ ) = x ⁰

a a dt V a 7 a dt V a 7

и так далее. На шаге с номером p получим ^ Hx ⁰ = H^{p + 1} (^) ^p ( ^ x⁰ ) = x ⁰ .

Откуда в силу нильпотентности оператора H , получим, что x ⁰ = 0.

Перейдем к рассмотрению второго уравнения системы. В силу [21] решение этого уравнения

f t          А имеет вид x1(t) = exp S j a (Z) dZ где S = L11M 1 е L (X 1). Откуда при x0 е X1, в силу замеча

^x 0 ,

V t 0            7

ния 4, решение имеет вид x ( t ) = X ( t , t ₀) x ₀. Теорема доказана.

Определение 7. Поток операторов X(•, •): R х R ^ L (X) называется потоком разрешающих операторов (или просто разрешающим потоком) уравнения (9), если для любого x0 е X вектор- функция x(t) = X(t, 10)x0 является решением уравнения (9) в смысле определения 5. Перейдем к рассмотрению задачи Шоуолтера-Сидорова

P ⁽ x ⁽ t 0 )^- x 0 ) = ⁰

для неоднородного уравнения

Lx = aMx + g

с функцией g :[ t ₀, T ) ^ Y . В дальнейшем будем использовать обозначение g ⁰ = ( I_Y - Q ) g .

Определение 8. Вектор-функция x е C 1 ([ t ₀, T ); X ) называется ( классическим ) решением (12), если подстановка этой вектор-функции в уравнение (12) делает его верным тожеством при некоторой вектор-функции g :[ t ₀, T ) ^ Y . Решение x = x ( t ) уравнения (12) будем называть решением задачи Шоуолтера-Сидорова (11) для уравнения (12) (коротко, задачи (11), (12)), если оно удовлетворяет условию (11) при некотором x ₀ е X .

Теорема 6. Пусть оператор M ( L , p ) -ограничен ( p е N ₀) и функция a е C p ^{+ 1}([ t ₀, T ); R ₊ ) .

Тогда для любой вектор-функции g:[t0, T) ^ Y такой, что Qg е C 1([t0,T); Y 1)   и

g0 е Cp+1([t0, T); Y0), и для любого начального значения x0 е X существует единственное решение xе C 1([t0,T);X) задачи Шоуолтера-Сидорова (11), (12), которое имеет вид tp

x ( t ) = X ( t , 1 0 ) x 0 + J X ( t , s ) L - ¹ Qg ( s ) ds - ^ H^kM 0 ¹

k = 0

' 1 d I k g ⁰( t ) _v a ( t ) dt J a ( t )

•

Если дополнительно выполнено условие согласования

( I x - P ) x 0 =- ^^H^kM 0 ¹

k = 0

( 1 d

k

_v a ( t ₀) dt _y

g ⁰⁽ t c ) a ( 1 0 ) ’

то функция (13) является единственным решением задачи Коши (9) для уравнения (12).

Доказательство. В силу теоремы 1 задача (11), (12) эквивалентна системе задач x ¹ = aL ^- M 1 x ¹ + L - 1 Qg ,      x 1 ( 1 ₀) = Px ₀,

Hx0 = ax1 + M01 g0,     x0(10) - любое на подпространствах X1 и X0 соответственно.

Уравнение в задаче (14) не является вырожденным, а, следовательно, решение задачи (14), в силу результатов [21], имеет вид x 1 ( t ) = X ( t , t ₀) x ₀ + J ₍₎ X ( t , s ) L - ¹ Qg ( s ) ds .

Перейдем к задаче (15). Выразим x0 из уравнения задачи (15) и получим x0 =1НХ0 a

M 01 g a

•

Продифференцируем это выражение, и применим оператор ^H, в силу уравнения получим x 0( t) + Mo1 g-^ = H1 0 a(t)

1 d x ⁰( t ) a ( t ) dt ^ a ( t )

л

У

HM ”’^L It [ g ⁰? ^ ) a dt ^ a ( t )

Л

У

•

Далее снова выразим x ⁰, продифференцируем это выражение, применим оператор ^ H , и так далее. На шаге с номером p получим

x ⁰( t ) = H P ^{+ 1}

p

4? d I ^ a ( t ) dt J

⁰/^\A P k 0 ~⁰/^\A x^t ) -У H^kM ^{- 1} 1 1 - I g -( t ) ( a ( t ) J ^ ₀ ⁰ I adt J ( a ( t ) J

откуда в силу нильпотентности оператора H , получим часть решения на X ⁰ в виде:

x ⁰( t ) = - j^ H^kM ^{- 1} f¹—) k = 0         <  ^adt J

(glI

Откуда получаем вид (13) для решения задачи Шоуолтера-Сидорова (11), (12).

Ясно, что если в начальный момент времени выполнено равенство

x ⁰( 1 0 ) = ( I x - P ) x 0 =- ^^H^kM 0 ¹

k = 0

k

——¹ _v a ( 1 ₀) dt J

g ⁰⁽ t 0 ) a ⁽ t 0 ) ,

то есть выполнено условие согласования, то функция (13) будет являться единственным решением задачи Коши (9) для уравнения (12). Теорема доказана.

Заключение. В дальнейшем планируется применить все полученные результаты для исследования задачи оптимального измерения в нестационарном случае. Такое измерение модели оптимального измерения позволяет учитывать, например, снижение чувствительности измерительного устройства [20].