Вырожденные уравнения Вольтерра типа свертки в банаховых пространствах и их приложения

Теория интегральных уравнений в абстрактных пространствах представляет интерес примерно с 60-х годов прошлого столетия. Этой тематике посвящена обширная библиография (см. монографии [1–3] и сопутствующие им обзоры литературы); среди отечественных исследований в данной области следует отметить работы И.Ц. Гохберга и М.Г. Крейна [4], М.М. Лаврентьева [5], А.Л. Бухгейма [6], И.В. Сапронова [7], Н.Д. Копачевского [8] и др. Во всех упомянутых работах изучаются классы уравнений Вольтерра с тождественным или непрерывно обратимым линейным оператором при внеинтегральном слагаемом (в главной части). Вырожденные интегральные уравнения в абстрактных пространствах представлены в современной литературе существенно меньшим числом публикаций, примерами таких являются [9–12]. Исследования систем интегральных уравнений с необратимой матрицей коэффициентов в главной части проводились М.В. Булатовым [13], В.Ф. Чистяковым [14] и др. Интегральные уравнения Вольтерра с вырождением в бесконечномерных пространствах впервые рассмотрены в пионерской работе Н.А. Сидорова [15], где изучалась однозначная разрешимость в классе непрерывных функций уравнения t

Bu ( t ) - j K ( t - s ) u ( s ) ds = f ( t ) 0

с фредгольмовым оператором B и операторнозначным ядром K(t) . В [16] к исследованию этой задачи впервые применен аппарат обобщенных функций со значениями в банаховых пространствах, ее однозначная разрешимость в классе распределений с ограниченным слева носителем доказана в [17] с помощью конструкции фундаментальной оператор-функции. В этих работах естественным образом возникала задача о построении обобщенного жорданова набора оператора B относительно оператор-функции K(t). Как отмечено автором [18, с. 112], применение разработанных методов становится весьма затруднительным, если K(t) имеет в точке t = 0 нуль кратности £ , т. е. K(0) = K'(0) = ... = K(£-1)(0) = O и K(^) (0) Ф O. Здесь и далее O - нулевой оператор. В этом случае неизвестно как строится жорданов набор оператора B. Подобная проблема возникает при изучении сингулярных линейных интегро-дифференциальных уравнений Вольтерра в банаховых пространствах с дифференциальной частью высокого порядка, в которой отсутствует хотя бы одно слагаемое наивысшего порядка группы младших производных.

Пусть E 1 , E ₂ - банаховы пространства, u = u ( t ), f = f ( t ) - неизвестная и заданная функции неотрицательного действительного аргумента t со значениями в E 1 и E ₂ соответственно. Рассмотрим интегральное уравнение

t

Bu ( t ) - J g ( t - s ) Au ( s ) ds = f ( t ),                                (1)

где B , A - линейные операторы, причем B e L ( E 1 , E ₂), A e Cl ( E 1 , E ₂) (т. е. A замкнут и D ( A ) = E 1 ), ядро g = g ( t ) - числовая функция. В этом случае K ( t ) = g ( t ) A , и он наиболее типичен для приложений. Будем предполагать, что оператор B является необратимым, а функция g = g ( t ) - аналитической в точке t = 0 и имеет в этой точке нуль кратности £ .

В работе [19] исследован вопрос существования и единственности решения уравнения (1) в классе распределений с ограниченным слева носителем в условиях фредгольмовости оператора B и наличия у функции g = g ( t ) в точке t = 0 нуля кратности £ . Показано, что в этих предположениях порядок сингулярности обобщенного решения возрастает на кратную £ величину. Представляемая статья посвящена изучению однозначной разрешимости уравнения (1) с ( B , p )-ограниченным оператором A . Применяется синтез идей теорий полугрупп операторов с ядрами Г.А. Свиридюка [20, 21] и фундаментальных оператор-функций вырожденных интегро-дифференциальных операторов в банаховых пространствах [17]. Подход оказался применимым к исследованию начальной задачи

t

Bu ⁽ N ) ( t ) - J g ( t - s ) Au ( s ) ds = f ( t ),                             (2)

u (0) = u 0 , u ‘ (0) = u 1 , .., u ⁽ N ^{- 1)}(0) = u n - 1 ,                          (3)

при аналогичных предположениях на операторные коэффициенты и ядро интегральной части.

Разрешимость абстрактных уравнений Вольтерра

В пространстве K + ( E 1 ) распределений с ограниченным слева носителем уравнение (1) принимает сверточный вид

I o ( 3 ( t )) * u ( t ) = f ( t ),                                              (4)

Здесь I_o ( J ( t )) = B ^ ( t ) - Ag ( t ) ^ ( t ), w( t ) = u ( t ) ^ ( t ), f ( t ) = f ( t ) ^ ( t ), 3 (t ) - функция Дирака, У ( t ) -функция Хевисайда, u ( t ) - классическое (сильно непрерывное) решение уравнения (1).

Определение 1. Фундаментальной оператор-функцией интегрального оператора I_o ( J ( t )) называется обобщенная оператор-функция s₀ ( t ) такая, что для любых v ( t ) e K + ( E 1 ) и w ( t ) e K + ( E ₂) справедливы равенства s_o ( t ) * I_o ( £ ( t )) * v ( t ) = v ( t ) , I_o ( J ( t )) * s_o ( t ) * w ( t ) = w ( t ) .

Смысл конструкции в том, что, если известен вид s o ( t ), то единственным решением уравнения (1) в K + ( E 1 ) ( обобщенным решением уравнения (1)) является ~( t ) = s_o ( t ) * f ( t ), в чем нетрудно убедиться, так же как это сделано, например, в работах [18, 19].

Изложению основных результатов предпошлем некоторые вспомогательные сведения из [20, 21], которые приведем в удобных для нас обозначениях.

Определение 2. Множество рв (A) = { дe C: (дВ - A) 1 e L (E 2, E1)} называется резольвентным множеством оператора A относительно оператора B ( B -резольвентным множе- ством оператора A), а оператор-функция (цВ - A)-1 - резольвентой оператора A относительно оператора B (B -резольвентой оператора A).

Определение 3. Оператор-функции R ^ ( A ) = ( ц В - A )¹ В и L ^ ( A ) = В( ц В - A ) ^{- 1} называются соответственно правой и левой резольвентами оператора A относительно оператора B (правой и левой B-резольвентами оператора A).

Определение 4. Оператор A называется спектрально ограниченным относительно оператора В ( ( В, о ) -ограниченным), если существует a >  0 такое, что { ц е C: Щ >  a }с р^в ( A ) .

Замечание 1. Пусть Г = { це C: Щ = r >  a }. Тогда, как показано в [20, 21], если оператор A спектрально ограничен относительно В , то операторы

P =    f R_JЦ ( A ) d Ц и Q = yr L L ( ( A ) d ц

2ni Г                 2ni Г являются проекторами в E1 и E2 соответственно, порождают разложения этих пространств в прямые суммы E1 = E0 © E1 = N(Р) © R(Р), E1 = E0 © E2 = N(Q) © R (Q). Действия операторов A и В расщепляются, при этом A0 : E0 ^ E0 , В1: E1 ^ E2 непрерывно обратимы, A1: E1 ^ E2 ограничен. Имеют место равенства QB = ВР, QA = AP.

Замечание 2. Если существует p е { 0 } и N такое, что ( A ₀ В 0 ¹) ^p + O 1 , но ( AВ ₀ 1 ) ^{p + 1} = O 1 , то бесконечно удаленная точка является несущественно особой точкой (либо устранимой особой точкой при p = 0, либо полюсом порядка p е N) В -резольвенты оператора A . В этом случае, согласно [20, 21], ( В , у ) -ограниченный оператор называется ( В , p ) - ограниченным .

Теорема 1. Пусть В е L ( E 1 , E ₂) , оператор A е Cl ( E 1 , E ₂) спектрально ограничен относительно В, g ( t ) е C ( t >  0) , тогда интегральный оператор I₀ ( ^ ( t )) = В ^ ( t ) - Ag ( t) 9 (t ) имеет на классе K + ( E ₂) фундаментальную оператор-функцию вида +∞                          +∞

£ о ( t ) = В ^{- 1} £ ( A В - ¹) k ^{- 1} Q ( g ( t Ж t )) ^{k - 1} - £ ( A 1 В 0 ) q A 0 ^{- 1}(l 2 - Q )( Y ( t )) q ^{+ 1}, k = 1                                     q = 0

здесь и всюду далее / ( t ) - обратный к g ( t ) У ( t ) элемент в сверточной алгебре D + , т. е. / ( t ) * g ( t ) У ( t ) = ^ ( t ), степень обобщенных функций понимается в смысле операции свертки, причем ( g ( t ) ^ ( t ))⁰ = 8 ( t ).

Доказательство. Согласно определению 1, следует показать, что I0 (^(t)) * £0 (t) = I2 5(t) и £0 (t) * Io (£(t)) = I1 5(t), где I1, I2 - тождественные операторы в E1 и E2 соответственно. Спра- ведлива цепочка равенств

I o ⁽ 5 ⁽ t )) * ^£ 0 ⁽ t ) = ^{( В} ^ ⁽ t ) ^- Ag ⁽ t Ж t )) * ^£ 0 ⁽ t ) =

+∞+∞

= ВВ1-1 £ (AВ1-1) kQ (g (t )^( t))k + ВВ^З( t) - В £ (A01 В 0) qA -1(I2 - Q )(y( t))q+1 - k=1

+∞+∞

- ABf1 £ (A1В-1)k-1Q (g (t )^( t))k + A £ (A 01 В0) qA»'(I. - Q )(y( t))q = k=1

+∞+∞

= £ (A1В1-1)kQ(g(t)^(t))k + Q^(t) - В0 £ (A01 В0)qA^(Хг- Q)(y(t))q+1 - k=1

+∞+∞

- £(A1В1-1)kQ(g(t)9(t))k + В0 £(A01 В0)U-U- Q)(Y(t))q+1 + AA(-1(Х2- Q)^(t) = k=1

= Q ^ ( t ) + (I 2 - Q ) 3 ( t ) = I 2 3 ( t ).

Далее, учитывая QB = ВР , QA = AP , получим

£ о ( t ) * I o ( 3 ( t )) = £ 0 ( t ) * ( В 8 ( t ) - Ag ( t ) 9 ( t )) =

+^+^

= B- У (A в:1)k BP(g(tЖt))k + B-1 BP^(t) - У (Ao1B0)q Ao'B(Ij- P)(y(t))q+1 -k=1

+^+^

- B-1 У (A1B-1)k1AP (g (t Ж t))k + У (Ao1 Bo) qA o-1 A (f - P )(y( t)) q = k=1

+^+^

= Bf1 У (A1Bf1)k1A1P(g(t)^(t))k + P^(t) - У (Ao'Bo)q+1(I1 -P)Y(t))q+1 -k=1

+^+^

- Bf1 У (A1Bf1)k1A1P (g (t )0( t))k + У (Ao1 Bo) q+1Ao1 A (f - P )(Y t)) q+1 + Ao-1 A (f - P Я t) = k=1

= P ^ ( t ) + (I 1 - P ж t ) = I 1 £ ( t ), что доказывает второе сверточное равенство и завершает доказательство всей теоремы. Теорема доказана.

Замечание 3. Если в теореме 1 дополнительно положить, что ^ - несущественно особая точка B -резольвенты оператора A, то +~

"^W R- 1 k-1З-НАЗ^ - 1         - 1 34 Л- 1/Т      ЗАААЗЧ + 1

S 0 (t) = B У (A1B1 )   Q(g (tЖ t))   - У (A o B o) Ao (I2 - Q)(Y( t)), k=1

p e { o } u N (см. замечание 2).

Следующая теорема, доставляющая способ построения у (t ), доказана в работе [19].

Теорема 2. Пусть g ( t ) e C ^{£ + 1}( t >  o) является аналитической функцией в точке t = o и в этой точке имеет нуль кратности £, т. е. g (o) = g '(o) = ... = g ⁽ ' ^{- 1)}(o) = o и g ^{( £ )}(o) ^ o , тогда обратным элементом y (t ) к g ( t) 0 (t ) в сверточной алгебре D + является обобщенная функция ^^{I1 + 1)}( _t )

Y(t) =           * (^(t)+ r(t)6(t)), g (£)(o)

g ^{( £ +} 1) ( t ) где r ( t ) - резольвента ядра ( _£ ) (o) '

Замечание 4. В условиях этой теоремы и ( B , p ) -ограниченности оператора A ,                                              р ,            ,            х(( q + 1)( £ + 1))(-л

So(t) = B-1^(t) *(I2 3(t) + Ro(t)У(t))Q- У(Ao-1Bo)qAo1(l2-Q) (g(£)(o))q21) *(3(t) + r(t)^(t))q+1 . Здесь Ro(t) - резольвента ядра A1 B-g(t), в терминах которой представлена первая группа слагаемых формулы в замечании 3. Рассмотрим последовательность из K + (E2) вида fk (t)^(t) = z т 1 , (^(t) + r(t)У(t))k * f (t)У(t), k e N, (g (£)(o)) k где r(t) из теоремы 2. Имеют место рекуррентные соотношения

^£_            t-                trtt-sV

g ( t) 0 (t ) * f k ( t) 0 (t ) = - 0 (t ) * f k - 1 ( t) 0 (t ), J g ( t - 5 ) f k ( 5 ) ds = J f k - 1 ( s ) ds , k e N.

^£ !                                 o                              o ^£ !

Поскольку известен вид s 0 ( t ), справедлива следующая

Теорема 3. Пусть выполнены условия теорем 1 и 2, оператор A e Cl ( E 1 , E ₂) является ( B , p ) -ограниченным, тогда уравнение (1) имеет единственное обобщенное решение, и, если

g(t) e C(p+2)(£+1) (t > o), f (t) e C(p+1)(£+1) (t > o; E2), то оно имеет вид

~( t ) =

tp

6 ( t ) -

R^-1Of(t ^-+R^\R (t—^Of (sARs - V ( Д^-1R W 4^-1Я -Г)ЛГ⁽⁽ q ^+1)(£+Wfl

B 1 Qf ⁽ t ) ⁺ B 1 J ^R o ⁽ t  s ) Qf ⁽ s ) ds   У ⁽ A o B o ) A o ^(I 2   Q ) f q + 1        ⁽ t )

o                         q = o

£ + 1 p

- ^^ ( A 0 ¹ B 0 ) q W - - 1[ q ] £ ⁽⁽ q ^{+ 1)( £ + 1)} - j ) ( t ), j = 1 q = ⁰

где используются обозначения замечаний 1, 2 и 4, а также

W j - 1[ q ] = j^( A 0' B 0 ) k A 01 (I 2 - Q ) f k ⁽+ q+Tj ^{- 1)}(0), q = 0,^, p , j = 1,^,£ + 1. k = 0

Теорема 4. Пусть выполнены условия теоремы 3, тогда, если

W j - 1[ q ] = 0, q = 0,^, p , j = 1,^,£ + 1, то уравнение (1) имеет единственное классическое решение tp

u ( t ) = B - ¹ Qf ( t ) + B 1 ^{- 1} J R 0 ( t - s ) Qf ( s ) ds - ^ ( A 0 ¹ B 0 ) ^qA 0 ' (I . - Q ) f q ⁽ + q 1 ^{+ 1)( £ + 1))}( t ).

q = 0

Начальная задача (2), (3) в пространстве K + ( E 1 ) принимает вид сверточного уравнения

I n ( 3 ( t )) * u ( t ) = h ( t ),                                           (5)

в котором IN (3(t)) = B^1N)(t) - Ag(t)^(t), ~(t) = u(t)^(t), а правая часть h (t) = In (3( t)) * p (t )0( t) + h 0( t )0( t)

включает не только свободную функцию уравнения (2), но и начальные условия (3). Здесь

t

N

h 0 ⁽ t ) = f ⁽ t ) ⁺ J g ⁽ t ^- s ) AP ⁽ s ) ds , P ⁽ t ) = ^ u j - 1

j = 1

t j ^{- 1}

( j — 1)!

Единственным решением уравнения (5) в K + ( E 1 ) ( обобщенным решением задачи Коши (2), (3)) является распределение ~( t ) = £_N ( t ) * h ( t ), где £_N ( t ) - фундаментальная оператор-функция интегро-дифференциального оператора I N ( £ ( t )).

Теорема 5. Пусть B е L ( E 1 , E ₂) , оператор A е Cl ( E 1 , E ₂) является ( B , p ) -ограниченным, а функция g ( t ) е C ^{£ + 1}( t >  0) - аналитической в точке t = 0 и в этой точке имеет нуль кратности £, тогда интегро-дифференциальный оператор I N ( ^ ( t )) = B ^ N ) ( t ) - Ag ( t ) ^ ( t ) имеет на классе K + ( E ₂) фундаментальную оператор-функцию вида

^£ N ( t ) = B

t N — 1

¹ —— 0 ( t ) * (I 2 5 ( t ) + R N ( t ) 0 ( t )) Q - ( N - 1)!

P ,         ,          x( q ( N + £ + 1) + £ + 1)m

- £ (A1 B0)q A1 (I2- Q)               +1() * (£(t) + r(t)^(t))q+1, q=0                         (g (0))

„ ,                                 ,      Г (t - s)N-1 z X , где Rn (t) - резольвента ядра AB]11---------g(s)ds .

0 ( ^N - 1)^!

Техника доказательства этой теоремы аналогична применяемой выше для интегрального оператора I0 (J(t)). Всюду далее используются обозначения hk(t)^(t) =            (^(t) + r(t)^(t))k *h0(t)У(t), kе N,

( g ^{( £ )}(0)) k

g ^{( £ + 1)}( t )

где r ( t ) - резольвента ядра ( _£ ) (0) (см. теорему 2).

Теорема 6. Пусть выполнены условия теоремы 5, тогда задача Коши (2), (3) имеет единственное обобщенное решение, и, если

g(t) е CpN+(p+2)(£+1) (t > 0), f (t) е CpN+(p+1)(£+1) (t > 0; E2), то оно имеет вид

~( t ) =

Г          .Vif-sV- - 1                 -- s(f-s-i-AN - 1 p ( t ) + B ,-1 [ ^ t -A)--- Qh ( s ) ds + B - 1 f f ( t s T ) —Rn ( t ) Qh ( s ) dTds - 1 J o ( N - 1)! 0          1 J o J o ( N - 1)! N ю

1 + 1

p

Z ( A o ^{- 1} B 0 ) ^q A o ^{- 1} (I 2 - Q ) h q + N ^{+ 1 + 1) + 1 + 1)} ( t ) ^ ( t ) - Z w j - 1[0] ^ ^{( 1 + 1 -} j ) ( t ) -

q = 0

j = 1

N + 1 + 1 p

Z Z (Ao'B0)q+1 Wj-Цq+1^((q+1)(N+1+1)+1   j) (t), j=1 q=0

где используются введенные выше обозначения, а также p wj-1[q] = Z(A-1B0)kA-1(I2-Q)hk—и1+1)+j-1)(0), q = 0,-,p, j = 1,-,N +1 +1. k=0

Замечание 5. Построенное в K + ( E 1 ) решение начальной задачи (2), (3) представляет собой сумму ~( t ) = u ( t ) ^ ( t ) + ta( t ), где функция u = u ( t ) удовлетворяет уравнению (2) и начальным условиям u ⁽ j ^{- 1)}(0) = u j _{- 1} - W j ₊₁ [ ₀ ] , j = 1,^, N , а ы = to (t ) является линейной комбинацией функции Дирака и ее производных. Оно совпадает с классическим ( N раз сильно непрерывно дифференцируемым) решением этой задачи, если порядки гладкости g = g ( t ) и f = f ( t ) увеличить еще на N и положить все W j _{- 1} [ _q ] = 0.

Теорема 7. Пусть выполнены условия теоремы 5 и g(t) e C(p+1)N+(p+2)(1+1) (t > 0), f (t) e C(p+1)(N+1+1) (t > 0; E2), тогда, если wj-1[q] = 0, q = 0,..., p, ное классическое решение

Л ( t - s ) ^{N - 1}

U ( t ) = p ( t ) + B ] ¹ f----------- ^{1 J} ₀ ( N - 1)!

p

.,...,N +1 +1, то задача Коши (2), (3) имеет единствен- t -v (t - v - t )N -1

Qh 0 ^{( v} ) ds + B 1 ¹ f j            ^ N ^{( T} ) ^Qh 0 ^{( v} ) ^{d T} d^{v -}

0 0 ^{( N - 1)!}

- £ ( A 0 1 b 0 ) A ^{- 1} (I 2 - Q ) h q '^{+1 + 1) + 1 + 1} ( t ). q = 0

Замечание 6. Порядки сингулярности (см. определение в работе [19]) обобщенных решений уравнения (1) и начальной задачи (2), (3) определяются порядками старших производных дельтафункции, входящих в эти решения, и равны ( p + 1)(1 + 1) и pN + ( p + 1)(1 + 1) соответственно. Таким образом, наличие у функции g = g ( t ) нуля кратности 1 в точке t = 0 приводит к увеличению порядков сингулярности обобщенных решений рассматриваемых задач на величину, кратную 1.

Приложения

Пример 1. Пусть Q = [ 0; h ] x [ 0; h ] x [ 0; h ] , h >  0 . Рассмотрим граничную задачу t         д ² u

(A-a)u(t,x,y,z) + p\(t-T)—y(T,x,y,z)dT = f (t,x,y,z), t>0, (x,y,z)e Q; .        дz u ( t, x, y, z )|( x, y, z )eд q = 0, которая описывает низкочастотные электронные (ионные) магнитозвуковые колебания во д 2 д 2 д 2

нем магнитном поле [22]. Здесь a * 0, в >  0 - параметры, A = —- +--- +---. Выбирая д x ² д y ² д z ²

E 1 = Hl^{L + 2}(Q) = { u ( x , y , z ) e W L ^{+ 2}(Q): u ( x , y , z )₍ x , _y , z _{) eд Q} = 0 } , E 2 = H^L (Q), L e { 0 } u N

внеш-

( H ⁰ (Q) = L ₂ (Q) - пространство функций с квадратом, интегрируемым по Лебегу на Q), а также

_ .          .. д полагая B = А-a, A = -в—, g(t) = t, сведем эту задачу к уравнению (1). Рассмотрим далее дz 2

однородную задачу Дирихле д2P д2P д2P .    _.

+ +-- X = 0, ф( x, у, z)0.

д x ² д у ² д z ^{2                         l(} x , ^у , z ^{) g Q}

Ее спектр с г ( А ) состоит из X _k m n

кое собственное число имеет вид

_П 2

= —— ( k ² + m ² + n ²), k , m , n g N , т. е. за необходимостью вся- h ²

пг

X и = —^ s , s g N. Кратность d(Л_к и) собственного числа h ²

Xkmn равна количеству различных решений (k, m, n) g N3 уравнения k2 + m2 + n 2 = s при заданном s g N. Учитывая известную теоретико-числовую теорему о представлении натурального числа суммой квадратов целых чисел [23, с. 344; р. 279], можно получить точную формулу d (X, m, n ) = I ( IX 4( d) - IS - k 2 i2),

k g N d g N k ² < s s - k ² | d

i g N

где х₄( d ) — характер Дирихле по модулю 4 числа d g N, S i j - символ Кронекера. Система собственных функций рассматриваемой однородной граничной задачи, ортонормированная в смысле скалярного произведения пространства H^L (Q), имеет вид

π k    π m    π n

P k mn ^{( x} , у , ^z ) = C k m n ^sin , ^{x sin} , у ^sin , ^z , k , m , n g N . hhh

2     2                   (п

Здесь Ck, m, n =- -------, Hk, m, n = I |T| k  1 m  2 n 3, a = a1 + a2 + «Y Пусть a g °(А) , h\hPk, m, n              0<| a I < LI h )

тогда B = А- a - фредгольмов оператор. Более того, нетрудно показать, что его нули P _{k mn} ( x , У , z ), k ² + m ² + n ² = s , не имеют A -присоединенных элементов. Тем самым, за доста

точностью A является (B,0)-ограниченным [20, 21]. Функция g(t) = t в точке t = 0 имеет нуль кратности t = 1. Из теоремы 3 вытекает п2

Следствие 1. Пусть а = —^- s g ° ( А ) , s g N , тогда краевая задача (6), (7) имеет единст-h ²

венное обобщенное решение, и, если f ( t , x , y , z ) g C²( t >  0; H^L (Q)) , то оно имеет вид

U ⁽ t , x , y , z ) = I    ¹ k ² + m ² + n ² <  s ^X k > ^m > ^{n a}

⁽ f P k , m , n ) h l (Q) ⁺

π n β ^t     π n β

+ h       ^a^ ^ShA/X   ^а⁽ t ^{T )(} f ^{, P k} , ^m ’ n ) H^{L (} Q)

^Г1^⁷^k , m , n      0 ^rk^'n , m , n ^a

^{d T} P k , m , n ^{( x} , у , ^z ) ^ ⁽ t ) ⁺

+I k 2+m 2+n 2 > s

Xk, m, n - a

⁽ f , P k , m , n ) h l (Q)

π n β ^t      π n β

^{d T} P k , m , n ^{( x} , у , ^z ) ^ ⁽ t ) ⁺

1    у     h ²

R   ¹   _ 2 2

P k ² + m ² + n ² = s ^п n

⁽ f t , P k , m , n ) _HL _(Q) ^ ⁽ t ) ^{+ (} f t |t = ₀, P k , m , n ) _HL _(Q) ^{S (} t ) ⁺

⁺ ( ^f\_t = ₀ ^, Ф k , m , n ) H L _(Q) ^ ( t ) Ф k , m , n ^{( x} , У , z ) .

Замечание 7. Если в условиях этой теоремы ⁽ f t = 0 ф , m , n ) H_{L (Q)} = ⁽Д = 0 ф , m , n ) H L _(Q) = 0, к ² + m ² + n ² = s , то ~( t , x , y , z ) = u ( t , x , y , z ) 0 ( t ), где функция u = u ( t , x , y , z ) является решением граничной задачи (6), (7) в классе C( t >  0; H^{L + 2}(Q)).

Аналогичные задачи физики плазмы рассматривались ранее. Например, модель ионнозвуковых волн изучалась А.А. Замышляевой, в том числе с применением вычислительных методов [24], в виде начально-краевой задачи для дифференциального уравнения соболевского типа высокого порядка относительно обобщенного потенциала электрического поля [22, с. 37].

Пример 2. Реализацией начальной задачи (2), (3) является задача Коши-Дирихле вида ар_п - U_ttxx + a ( « 2 u_t - U txx ) + b ( « 3 u - u xx ) = f ( t , x ), t >  0, x e ^[ 0; h ] ;             (8)

u ( t , x )| _t = ₀ = u 0 ( x ), U t ( t , x )| t = ₀ = u 1 ( x ), x e [ 0; h ] ; u ( t ,0) = u ( t , h ) = 0, t >  0,         (9)

которая при а2 = а, заменой v(t, x) = ut (t, x) + au (t, x) сводится к начально-краевой задаче t а1 vt - vtxx + bje-a(t-T)(a3v(t,x)-vxx(t,x))dT = f (t,x) -b(a3u0(x) -u0(x))e-at, t > 0, xe[0; h]; (10) 0

v ( t , x )| t = ₀ = u 1 ( x ) + au ₀( x ), x e [ 0; h ] ; v ( t ,0) = v ( t , h ) = 0, t > 0.           (11)

Здесь a _x, a ₂, a ₃, a , b e R - ненулевые параметры. Уравнение (8) описывает продольные колебания упругого стержня с учетом инерции и массовой нагрузки. В современной научной литературе это уравнение и его многомерные аналоги именуют уравнениями Буссинеска-Лява [25].

Задача Коши-Дирихле (10), (11) является частным случаем начальной задачи (2), (3) при d ²            , d ² х

N = 1, B = a —2 , A = -b(a —-y), g(t) = e  , dx2 dx если пространствами E1 и E2 выбрать, например, HД2 и H[Lh], Le {0}uN. Введем в рассмот-

_2 2

П n рение собственные числа ^ =--^—, n e N, краевой задачи ф (x) = Хф(x), ф(0) = ф(h) = 0 , и h 2

систему соответствующих им собственных функций

^ n          ²

Ф п ^{( x} ) = C n Sin — ^x , C n = ----, ^u n h          N hu n

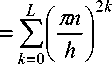
ортонормированную в H[L h]. Пусть a1 = Xs, s e N, тогда оператор B - фредгольмов, причем его нуль ф8 (x) e N(B) не имеет A -присоединенных элементов. Значит, оператор A спектрально ограничен относительно B и ^ является устранимой особой точкой относительной резольвенты (pB - A)-1. Функция g(t) = e-at при t = 0 не обращается в нуль, т. е. ^ = 0 . Сформулированное далее утверждение является следствием теоремы 6.

^{П s}

Следствие 2. Пусть a =--

¹ h²

s e N , тогда начально-краевая задача (10), (11) имеет

единственное обобщенное решение, и, если f ( t , x ) e C 1 ( t >  0; H [ Lh ] ) , то оно имеет вид:

v ( t , x ) = u 1 ( x ) + au ₀( x ) + V —-— n ^ s ^a 1 - ^ n

t wn (t) + J rn (t - T) wn (T)dT 0

Ф п ^{( x} ) ^ ⁽ t ) ⁺

+

b ( a ₃ - a 1 )

( f t

^{+ af - b( a} 3 ^- « 1 ^{)( u} 1 ^{+ au} 0 ), Ф s ) H [ L _0; h ] 0 ⁽t ) ⁺ ( f i t = ₀

-

^{b ( a} 3 ^{- a} 1 ) ^u 0 ^, Ф s \l L   5 ⁽t ) Ф s ^{( x} ),

^H [0; h ]

t b                              1

где w n ( t ) = ( f ( τ , x ) d τ - ( α 3 - λ n ) ( t ( u 1 + au 0 ) + (e ₀ a                      a

-

at

-

1) u ₁ ) , ϕ _n ) _H

L

[0; h ]

, r_n ( t ) – резольвента ядра

b γ n (e

-

at

-

a

1) , γ n =

α 3

-

λ n

α 1 - λ n ,

которая определяется формулами

r_n ( t ) =

-

2 b γ _n

a

t

n

-

a

e

sin

4 b γ _n

-

a

t при всех n ∈ N таких, что 4 b γ n

-

a ² > 0 ;

r_n ( t ) =

-

2 b γ _n

a

t

a ² - 4 b γ n

e

sh

a ² - 4 b γ _n

t при всех n ∈ N таких, что 4 b γ n

-

a ² <  0 ;

a a2 - t rn(t)=- 4 e 2

при всех n ∈ N таких, что 4 b γ n - a 2 = 0 .

Замечание 8. Если f ( t , x ) ∈ C²( t ≥ 0; H _[ ^L _{0; h ]}) и

( f    -b(α1-α3)u0,ϕs) L =( f′   -b(α1-α3)u1,ϕs) L =0, t 0                             H[0;h]          t 0                             H[0;h]

то v~(t, x) = v(t, x)θ(t), где функция v = v(t, x) представляет собой решение начально-краевой за дачи (10), (11) в классе C1(t > 0; H[L+2]).

Вопросы однозначной разрешимости различных начально-краевых задач для уравнения (8) и его многомерных аналогов при α2 = α1 , α1 ∈ σ(Δ) изучены в цикле работ А.А. Замышляевой и ее учеников. Случай α2 ≠ α1 , α1 ∈ σ(Δ) , рассмотрен в [18]. Представленные в данной работе результаты исследования задачи Коши–Дирихле (8), (9) в интегро-дифференциальной форме (10), (11) согласуются с полученными ранее.

Работа проводилась при финансовой поддержке Российского фонда фундаментальных исследований в рамках научного проекта № 16-31-00291 мол_а.