Вывод нелинейного объекта третьего порядка на заданное движение

Работа посвящена синтезу программного управления для нелинейного объекта управления с целью вывода его на заданную траекторию. В основе синтеза лежит решение задачи оптимального по быстродействию управления, с помощью которого осуществляется поэтапный перевод объекта на заданное движение.

Постановка задачи. Рассматривается объект управления, который описывается следующей системой нелинейных дифференциальных уравнений:

^^ - -^1(1)22(0 + хз(<),     (I)

^ = -0Ъ,{«)-

-s3(t)x3(t)sign(a:3(t)) + Ц<), где $i(t) - переменные состояния объекта, г = 1,2,3; |u(t)| < 1 - управляющее воздействие; y(t) = ari(t) - управляемая переменная, выход объекта. Требуется перевести выход объекта из начального нулевого состояния на заданную траекторию, которая описывается следующей линейной функцией времени:

г(4) = 0,0144 + 0,62.           (2)

Решению задачи перевода нелинейного объекта на заданную траекторию посвящено достаточно много работ [3], где также рассматриваются некоторые методы синтеза нелинейных систем управления с полиномиальными нелинейностями. В данной работе приводятся результаты расчета программного управления для частной задачи быстродействия с последующим многократным применением этого управления. Показано, что с некоторой приведенной погрешностью можно осуществить перевод объекта на заданную траекторию (2) объекта управления (1).

Описание алгоритма синтеза программного управления. Во-первых, следу ет иметь в виду ограничения, накладываемые на модели нелинейных объектов управления. Они описываются обыкновенными дифференциальными уравнениями с постоянными коэффициентами.

Решения дифференциальных уравнений являются гладкими функциями. В систему дифференциальных уравнений управляющее воздействие входит линейно и имеет симметричное ограничение на свою величину, т. е. когда |ц(4)| <  17™, где 47_т - максимально допустимая величина. Для подобных объектов в задаче быстродействия оптимальное правление носит релейный характер с интервалами управления не более п, где п - порядок объекта (количество дифференциальных уравнений) [2].

Предлагается решать нелинейную задачу быстродействия для краевых условий, когда правая граница по управляемой координате является достаточно малой. В частности, для приведенного примера краевые условия имеют вид: X (0) = [0; 0; 0] — левая граница, X(tfc) = [zifc;0;0] — правая граница, где tk - минимальное время перехода в состояние X(t_k), т_гк >  0.

Расчет моментов переключения релейного управления был выполнен на основе численного алгоритма, приведенного в [1]. В отличие от других алгоритмов, решающих нелинейную задачу быстродействия, в нем не требуется задания начального приближения по определению моментов переключения. Он численно, программным путем определяет условия «сшивания» траекторий с последующим расчетом временных отрезков, где это происходит.

Когда определены моменты переключения 41,4г,4з = tk, то программное управление с моментами переключения ii, t^, ts многократно используется для систем уравнений (1), с учетом того, что происходит накопление временных отрезков, на каждом из которых управляющее воздействие определяется с линейным преобразованием координат по оси времени, а переменные состояния имеют начальные значения, полученные при гаггегрировании дифференциальных уравнений на предыдущем временном отрезке. Подбор моментов переключения осуществляется за счет правой начальной границы х^ и величины допустимого управления. Процесс подобного моделирования не представляет особых проблем в такой высокоразвитой системе математических и инженерных расчетов, как MATLAB. Именно в ней реализованы рассматриваемые алгоритмы. Их можно практически полностью автоматизировать.

Естественно ожидать, что численные расчеты влекут за собой погрешности, которые будут накапливаться при многократном использовании управляющего воздействия для заданной системы дифференциальных уравнений.

Результаты синтеза программного управления для перевода нелинейного объекта на заданную траекторию. При ведем условия, для которых были получены результаты синтеза программного управления, переводящего выход объекта (1) на заданную траекторию (2): (0) — [0; 0; 0] - левая граница, X(tfc) — [0,2;0;0] -правая граница, U_m _ i_rtt = 0,52, t₂ = l,44,t₃ = 1,85.

Результат многократного приложения управляющего воздействия с предварительно рассчитанными моментами переключения к системе (1) показан на рис. 1.

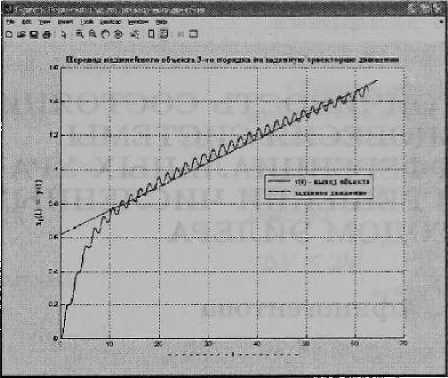
Ptic. 1. Пример вывода нелинейного объекта на заданное движение

Как видно из рис. 1, в достаточно большой области движение нелинейного объекта осуществляется вдоль заданной траектории.

Оценка отклонений движения нелинейпо- го объекта от заданного движения дается с помощью приведенной погрешности, которая выражается в процентах от максимального значения для линейной функции (2).

Характер изменения приведенной погрешно сти показан на рис. 2.

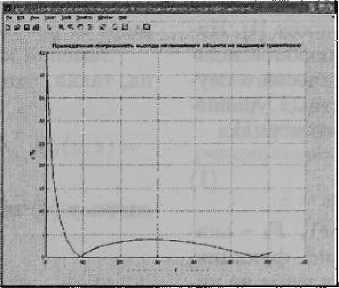
Рис. 2. Оценка погрешности выхода объекта на заданную траекторию

Как видно из рис. 2, погрешность не превосходит 5 % (обычное инженерное требование) на достаточно большом временном отрезке. Таким образом, оптимальное по быстродействию управление может быть использовано в задаче вывода нелинейного объекта на заданную траекторию.