Взаимное действие эффектов естественной бианизотропии и искусственной киральности среды на распространение электромагнитных волн
Автор: Зейде К.М.
Журнал: Физика волновых процессов и радиотехнические системы @journal-pwp
Статья в выпуске: 1 т.27, 2024 года.
Бесплатный доступ
Обоснование. В настоящей статье рассматриваются взаимные действия специфических эффектов среды на распространяющиеся в ней электромагнитные волны. Объектом исследования стал движущийся диэлектрик, который в состоянии покоя проявляет бианизотропные свойства, т. е. является синтетическим материалом, в частности киральным с Ω-частицами. Бианизотропные материальные уравнения являются наиболее общими для описания эффектов взаимодействия сложной среды с электромагнитным излучением. Их изучение и анализ оказываются заметной научной проблемой. Естественная бианизотропия является свойством природных сред, находящихся в особых условиях (состояние движения, внутренние токи и диффузионные процессы), тогда как искусственная бианизотропия суть неотъемлемое свойство самого синтетического материала (композитного материала, материала с различными метачастицами).
Бианизотропия, киральность, гиротропия, пространственная и временная дисперсия, движущаяся среда, распространение электромагнитных волн, эмерджентность
Короткий адрес: https://sciup.org/140303726
IDR: 140303726 | УДК: 537.834 | DOI: 10.18469/1810-3189.2024.27.1.9-18
Текст научной статьи Взаимное действие эффектов естественной бианизотропии и искусственной киральности среды на распространение электромагнитных волн
Однородный и изотропный в состоянии покоя диэлектрик при взаимодействии с внешним электромагнитным полем, пребывая в состоянии движения, начинает демонстрировать бианизо-тропные материальные свойства [1; 2]. Этот хорошо известный, описанный во многих трудах факт обладает как теоретической, так и практической значимостью [3–5]. Детектирование слабой бианизотропии суть ряда новых методов бесконтактной дефекто- и структуроскопии, о чем также указывается в приведенных выше материалах.
В подавляющем количестве работ по изучению электромагнитных свойств движущейся диэлектрической изотропной среды, применяется тот или иной эквивалентный переход к статическому случаю, т. е. задача равносильно (или с аппроксимациями) формулируется для частотной области анализа. Так, метод RFT (rest frame theory), применяющийся при решении задач дифракции [6], является неравносильным переходом; дополненная
интерпретационная модель равносильного перехода описана в [7] – в ней необходимо учитывать время установления бианизотропных материальных свойств. Была также отмечена возможность использования метода обобщенного эйконала при решении задач дифракции и распространения электромагнитных волн в движущихся изотропных средах [8–10]. В диссертации [11] доказывается справедливость применения т. н. метода раскручивания, что фактически является обратным переходом от статической задачи к динамической – противоположный переход также возможен.
В контексте данной работы естественная бианизотропия является свойством природных сред, находящихся в особых условиях, тогда как искусственная бианизотропия суть неотъемлемое (и зачастую определяющее) свойство самого синтетического материала [12]. Как указывалось выше, наиболее распространенным методом получения естественной бианизотропии выступает просто инициация движения любой диэлектрической среды. Классическим примером является движе-
[м^^е © Зейде К.М., 2024
ние сплошной среды, например жидкости (чаще всего воды) или газа [5]. Другим распространенным примером природной бианизотропии является дрейфующая плазма [4; 6; 11]. Искусственная бианизотропия объединяет собой множество новых функциональных синтетических материалов: композитные материалы, математериалы, материалы с Ω-частицами и т. д. [12]. В дополнение укажем, что природная бианизотропия во всех случаях будет проявлением движения заряженных частиц в среде. Кроме непосредственного движения самой среды бианизотропия может быть результатом протекания микротоков в неидеальных диэлектриках, диффузии заряженных частиц в нем или механической деформации.
В данной работе рассматривается взаимное действие эффектов естественной и искусственной бианизотропии в контексте их аддитивного влияния и возможной эмерджентности в выбранной системе отсчета (СО). Объектом для настоящего исследования служит движущаяся среда, которая в состоянии покоя уже проявляет бианизотроп-ные свойства. Целью работы стало обобщение уже имеющихся данных и на их основе получение аналитических выражений, которые могут быть затем эффективно использованы для планирования натурного эксперимента, создания новых вычислительных техник для решения прямых и обратных задач дифракции электромагнитных волн.
1. Формулировка проблемы
В [3] приводится классический вывод материальных уравнений для движущейся однородной изотропной среды в лабораторной СО. Алгоритм сводится к записи материальных условий для диэлектрика в движущейся СО, а затем с использованием преобразования Лоренца для полей и источников осуществляется переход к материальным уравнениям Максвелла – Минковского. В простейшем случае в движущейся СО диэлектрик является однородным и изотропным, т. е.
D ' = s E ' , B ' = ц И ' , j ' = o E ' .
Если к (1) применить преобразования Лоренца для полей (линейная скорость движения среды обозначена v ), то:
E '= E, +a ( E 1+ v x B ) , („ v x E )
B = в +a| B i —2 I ,
V c 2 )
. f vx H
D = D + a D +--
II 1 2
V c
H '= Иц +a ( H 1- v x D ) .
И для источников:
a v j
P = ap—-1, c 2
j ' = a j - avp .
С учетом того, что в (2) и (3):
a = , ,
P = -, c получим известную запись:
v x H
D + =s ( E + v x B ) ,
c2
v x E
B - =ц ( И - v x D ) ,
c2
j = vp + 0 ( E + v x B ) . a
В (5) мы учли, что Z|| + a Z i = Z , где Z - произвольный вектор, участвующий в трансформации.
Если в штрихованной системе отсчета покоится анизотропная среда, электродинамические параметры которой определяются через матрицы s и ц , то (5) сохраняет свой вид mutatis mutandis . Более интересный случай рассматривается в работе [13]. Материальные уравнения в штрихованной системе отсчета выглядят следующим образом:
D ' = ( s + ^2 ) E ' + j ц^ И ' , (6) В ' = ц И '- ME' .
Система уравнений (6) есть материальные выражения для киральной биизотропной среды с коэффициентом киральности £ . Применим (2) к (6):
D + v x H = s ( E + v x B ) + (7)
c2
+ ц^(Е + vx B) + j (И -vx d)], b - V^ E = ц(и -vxd)- j ^(e+vx B).
c2
Аналогичным образом может быть получена запись материальных уравнений для бианизо-тропной среды, главным отличием которых от показанных в (6) и (7) является то, что электродинамические параметры среды определяются через матрицы s и ц (см. [13]). В данной статье мы огра- ничимся данным уровнем описания, так как вы- вод этих уравнений не является целью настоящей работы.
Вместе с характерными граничными условиями и микроскопическими уравнениями Максвелла материальные уравнения (7) могут быть использованы для аналитического решения дифракционной задачи, как это было сделано в [14]. В этой работе нас интересуют электродинамические характеристики среды, поэтому мы нацелены в первую очередь на получение постоянной распространения электромагнитных волн в ней. Для простейшего случая (5) это было сделано, например, в [11; 15; 16]. В [9] приведено обобщение для учета действующих в системе сил инерции. Постоянная распространения может быть использована для получения уравнения эйконала [10]. Так, в работе [17] предлагается подход получения индекса рефракции движущейся бианизотропной среды (в частности, плазмы) через вектор поляризуемости среды, включенный в состав уравнений Максвелла.
Имея выражения (7), используем классический подход, описанный в [15]. Применяем уравнения Максвелла – Минковского
V x E = j мВ, (8)
Vx H = - jmD + J,V-D = p,
V-В = 0
к (7):
Vx H = - j м s ( E + v x В ) +
+ P^(E + vx В) + j (H-vx D)]-^ c2
+ J ,
Vx E = j м
ц(н -vx D)-j ц^(Е + vx В j + ^xH c2
Искомое волновое уравнение может быть получено и из системы (9), однако кажется проще применить уравнения (8) сначала к штрихованной системе отсчета (6), найти волновое уравнение в движущейся системе, а затем перейти к лабораторной через преобразования Лоренца (2) и (3). Такой порядок действий был использован, например, в [18]. Вывод уравнения Гельмгольца для рассматриваемого случая приведен в приложении.
-
2. Статическая бианизотропия и эффекты киральности
Бианизотропные материальные уравнения являются наиболее обобщенными для описания эффектов взаимодействия среды с электромагнитным излучением. Детальный обзор всех возникающих в процессе распространения ЭМВ в таких средах эффектов предложен в [19]. В данном разделе мы рассматриваем эффекты в неподвижной СО, таким образом, материал [10] в незначительной степени утрачивает свою общность по части некоторых наблюдаемых нематериальных эффектов. Тем не менее мы выделим ряд явлений, которые находятся в области изучения электродинамики движущихся сред [10]. Таковыми являются: гиротропность, пространственная и временная дисперсии. Ковариантная форма материальных уравнений для бианизотропной среды приведена в [20].
На основе статической гиротропности среды в работе [21] было предложено изучать ее бианизо-тропные свойства. Близкое по смыслу исследование описано в [22], где приведено аналитическое решение дифракционной задачи. Рассеяное от ги-ротропной среды электрическое поле может быть представлено в виде
Esc = eYzE 0 [ xcos (pgz)-y sin (в gz )]. (10)
Выражение (10) описывает рассеянное поле при распространении падающего линейно поляризованного поля с амплитудой E 0 вдоль оси z . Величина в g = ^м . Таким образом, аргументом тригонометрических функций являются угол поворота плоскости поляризации, т. е. магнитуда гиротроп-ного эффекта 9 = в g Z • Очевидно, что угол поворота плоскости поляризации зависит от оптического пути, пройденного волной внутри гиротропной среды. Постоянная распространения здесь и далее обозначена у .
Пространственная дисперсия проявляется в нарушении пространственной локальности поведения электромагнитного излучения в среде. Нарушение локальности обнаруживается на малых масштабах дальности [23] и описывается на уровне составных частиц кирального вещества. Пространственная дисперсия в естественных средах характерна для плазмы [24; 25], которая, как уже было отмечено выше, является классическим примером бианизотропного вещества [17].
Условие нарушения локальности в неподвижной СО может быть получено напрямую из (6), применяя (8) для циркуляции полей:
D = бЕ + Z[sVx E - j ^Vx h], (11) В = цH + Z[pVx H + j ^Vx E],
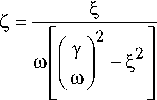
Из (11) видно, что материальные параметры зависят не только от падающих полей, но и от их пространственных производных, что определяет пространственную дисперсию среды [19]. Магнитуда этого эффекта определяется величиной Z , которая зависит от коэффициента киральности среды и циклической частоты распространяющейся волны. С ростом частоты магнитуда эффекта пространственной дисперсии уменьшается, потому что чем меньше длина волны, тем все меньший масштаб элементов среды вовлекается в процессы, описывающие условия ее распространения в ней.
Временная дисперсия более характерное и распространенное явление, в том числе для изотропных сред, особенно при их анализе в широком диапазоне частот. Наиболее часто временная дисперсия описывается функцией зависимости у ( ю ) и объясняется множеством причинностных моделей [26; 27] в рамках выражения Крамерса – Кро-нига [28; 29].
-
3. Взаимное действие эффектов
В данном разделе мы рассматриваем движущуюся среду, которая в состоянии покоя также демонстрирует бианизотропные свойства. Наиболее ярким примером такого объекта исследования является либо жидкий киральный диэлектрик, находящийся в состоянии движения сплошной среды, либо жесткая осесимметричная диэлектрическая матрица с Ω-частицами, находящаяся в состоянии вращательного движения. В обоих случаях граница рассеяния на объекте не изменяется с течением времени.
Вначале рассмотрим эффект гиротропии среды. Запишем уравнение Коши – Гельмгольца линейной скорости малой частицы внутри движущейся сплошной среды:
v„ = v + -rot vx r + Dr, (12) a2
где D ˆ – тензор скорости деформации. Если мы предположим, что линейная скорости движения среды всюду постоянна как по величине, так и по направлению, тогда v a = v . В этом случае эффект естественной гиротропии отсутствует и поворот плоскости поляризации соответствует статическому случаю. Этот факт подтверждается в [8; 30].
Поворот плоскости поляризации электромагнитной волны, распространяющейся в движущемся изотропном диэлектрике, есть [8]:
0 = " 1 cn
1 rot v- srotv ds.
С учетом того, что ^rotv=Q, где ^ есть угловая скорость движения среды, которая в указанном случае по условию равна нулю, из (13) следует, что угол поворота плоскости поляризации также равен нулю. Укажем, что в (13) интегрирование ве- дется по лучевому вектору s, что может соответствовать пройденному оптическому пути в гиро-тропной среде. Можем отметить, что гиротропия проявляется только в том случае, когда движущаяся среда обладает ненулевым вектором ускорения. Это утверждение полностью согласуется с общей теорией относительности [31; 32].
Если же мы рассматриваем реальное движение жидкости в трубах, особенно турбулентное, то, естественно, введенное выше условие не выполняется (Q ^ 0). На основании этого мы можем сде- лать два важных вывода.
-
1. Турбулентно движущаяся сплошная кираль-ная среда проявляет свойства как естественной, так и искусственной гиротропии. С учетом (10) и (13) можем записать результат простого аддитивного взаимного действия:
-
2. Учитывая, что выражение (12) описывает скорость частицы в турбулентном потоке, логично предположить, что при определенных условиях, которые должны быть рассмотрены отдельно, Ω-частица среды может испытывать момент силы в потоке, что приведет к ее вращательному движению с угловой скоростью, пропорциональной Ω, а также к возможной деформации. Эффект вращения и деформации метачастицы на распространяющееся электромагнитное поле в среде требует отдельного изучения. Для такого изучения необходимо применение (вероятно, и разработка) новых численных методик моделирования. Одним из возможных подходов к многомасштабному моделированию динамики отдельных частиц в движущейся среде является метод
П(бц- 1) 0 = z ^ю + —
2 cn
.
Выражение (14) хорошо иллюстрирует аддитивное действие. В скобках у нас имеется непосредственная сумма магнитуд целевого эффекта, вызванного искусственной и естественной бианизотропией.
дискретных элементов. Он уже был применен для анализа электрофизических свойств движущейся жидкости с мелкодисперсионным металлическим порошком в ее потоке [33]. Возможно, такая динамика метачастиц в среде может проявить себя в эмерджентности системы. В данном контексте нас не интересуют эффекты временной области, так как они не связаны с бианизотропными свойствами среды. Тем не менее мы можем прогно- зировать переход среды в принципиально новое состояние, при котором движущаяся киральная среда обладает еще и произвольно вращающими- ся метачастицами.
Если теперь мы будем рассматривать жесткую осесимметричную диэлектрическую матрицу, в которую помещены и зафиксированы в своих положениях метачастицы, тогда мы вновь будем иметь дело с простым аддитивным эффектом. Мы можем с определенной степенью условности и в этом случае применить формулу (12), но уже для общей цели. Так, линейная скорость цели есть произведение ее угловой скорости на радиус цели. Угол поворота плоскости поляризации также может быть получен из (14). Детальные выражения для случая вращения твердого тела приведены в [9; 11; 16].
Следующий эффект, взаимное действие которого мы рассмотрим, это пространственная дисперсия движущейся киральной среды. Аналогично тому, как было получено выражение (11), мы можем получить материальные уравнения в движущейся СО, применяя (8) к (7) для циркуляции полей. Тем не менее более показательно развернуть формулу для магнитуды этого эффекта, приведенную в (11). В нее входит постоянная распространения, которая для случая движущейся киральной среды является результатом решения волнового уравнения, показанного в приложении. Это решение аналогично описанному в [11; 14; 15; 18]. Используя нотацию теории возмущений, можем записать:
z=- to
ГГт ° +
^
-^ 2
Для получения (15) мы приняли, что состояние движения среды является малым возмущением состояния всей системы, таким образом, величина с надстрочным индексом «0» есть величина, определяемая в неподвижной СО, тогда как величина с надстрочным индексом «1» есть величина, определяемая в движущейся СО. Из формулы (15) видно, что пространственная дисперсия обладает аддитивным эффектом в части постоянной распространения электромагнитных волн в движущейся киральной среде.
Здесь оказывается важно разделить масштабы рассмотрения элементов среды. В масштабе рассмотрения динамики отдельной метачастицы ки-ральной среды может быть описан эффект искусственной пространственной дисперсии, тогда как на масштабе рассмотрения динамики отдельного электрона в движущейся среде может быть описан эффект естественной пространственной дисперсии [34]. Моделирование динамики электрона во вращающейся системе отсчета описано в [35]. Аналогичным образом может быть получено решение для динамики Ω-частицы. В настоящем изучении нам важно лишь констатировать факт того, что эффекты пространственной дисперсии в движущемся киральном диэлектрике являются эффектами разных масштабов и требуют проведения многомасштабных исследований.
В работе [36] исследуется возможность описания среды движущегося диэлектрика через его индекс рефракции, что эквивалентно переходу к неподвижной СО, но с измененными параметрами диэлектрической и магнитной проницаемостей объекта (переход такой не может быть осуществлен мгновенно из-за инертности частиц среды [7]). Кроме всех прочих очевидных фактов такого перехода (изменение индекса рефракции среды, изменение оптической траектории, изменение угла между волновым вектором и вектором Пойтинга [37] и т. д.), это означает и изменение причинност-ной модели временной дисперсии среды. Возможной эмерджентностью системы может является возникновение магнитных свойств движущегося диэлектрика ( ц r ^ 1), который в состоянии покоя был немагнитным ( ц r = 1). Здесь не ведется речь о возникновении магнитных полей, продуцируемых направленным движением заряженных частиц в среде. Для эквивалентного перехода в материальных уравнениях от изотропного к бианизотроп-ному диэлектрику, как показано в [7], необходимо пересчитывать как диэлектрическую, так и магнитную проницаемости среды, причем они пропорционально связаны между собой через коэффициент бианизотропной связи.
Заключение
Обозначим далее наиболее значимые выводы настоящего исследования. Во-первых, в статье
Зейде К.М. Взаимное действие эффектов естественной бианизотропии ...
Zeyde K.M. Reciprocal action of natural bianisotropy and artificial chirality ...
было показано, что гиротропность среды обладает не только простым аддитивным эффектом, но и при некоторых специфических условиях может быть связана с эмерджентностью системы. Система может приобрести новые свойства, если метачастицы будут вовлечены в сложное движение вместе с движением самой среды. Во-вторых, взаимное действие пространственной дисперсии движущейся киральной среды в целом имеет разные масштабы по дальности: если искусственная пространственная дисперсия обнаруживается на уровне метачастиц, что может считаться мезоуровнем, то естественная пространственная дисперсия обнаруживается на уровне элементарных частиц – электронов. В этом контексте было предложено использование метода дискретных элементов для проведения многомасштабного вы- числительного эксперимента. Это также означает, что пространственная дисперсия имеет аддитивный эффект только на постоянные распространения электромагнитных волн, а не на магнитуду целевого эффекта. Это связано с тем, что в данном случае может быть успешно применена теория возмущений, в рамках которой движение среды является малым возмущением состояния системы. В-третьих, была исследована временная дисперсия, которая не обладает простым аддитивным свойством, потому что даже изотропная среда при ее движении приобретает принципиально новые материальные свойства бианизотропии. Здесь также можно указать о возможной эмерджентно-сти системы, в частности о появлении магнитных свойств среды, которая в состоянии покоя их не проявляла.
Приложение. Уравнение Гельмгольца для движущейся киральной биизотропной среды
Из первых двух уравнений (8) имеем:
B '=
Vx E ' j to ’
J '-Vx H ' j to
Теперь подставляем выраженные величины в (6):
Vx E ' j to
p H '- j pS E ' ,
J V H = a E ' + j pS H ' .
jto где a = s + pS2 • Выражаем одну полевую величину через другую, например в первом уравнении предыдущей системы:
H ' =
Vx E ' j top
+ jSE
Подставляем выраженную величину во второе уравнение системы:
|
"VxF/ J '-Vx ----+ j S E ' ---j ---- = a E j to |
' + j pS -— + j S E ' . j top J |
Все последующие манипуляции направлены на упрощение волнового уравнения. Порядок действий для левой части может выглядеть следующим образом:
J '-Vx
Vx E '
. j top
+ j S E '
|
J '- |
VxVx E ' +Vx j S E ' . j top J |
J '-
V- ( V- E ' ) -V 2 E '
j top
+ Vx j S E '
j to
j to
j to
•
Для получения однородного уравнения исключим из системы внешние источники, таким образом, окончательная запись левой части есть:
V 2 E ' VxS E ' — to 2 p to
Правая часть:
aE' + /ц^ V-E- + j^E' = aE' + _ jюц _
^-ц^ = E'fa-^ VV-E ю ю
.
Теперь приравниваем правую и левую часть, приводим к однородному виду и применяем (2) для перехода к лабораторной СО:
V2-Ге + a-vx b] V-Ге + a-v- b!^^ - 2^---^^ - (a - ц^2)[E + a ■ v x b] = 0.
Полученное уравнение может быть далее упрощено с использованием (8), что в итоге приводит к окончательной записи однородного волнового уравнения.
Список литературы Взаимное действие эффектов естественной бианизотропии и искусственной киральности среды на распространение электромагнитных волн
- Kong J.A. Image theory for bianisotropic media // IEEE Transactions on Antennas and Propagation. 1971. Vol. 19, no. 3. P. 451–452. DOI: https://doi.org/10.1109/TAP.1971.1139951
- Arnaud J.A., Saleh A.A.M. Theorems for bianisotropic media // Proceedings of the IEEE. 1972. Vol. 60, no. 5. P. 639–640. DOI: https://doi.org/10.1109/PROC.1972.8711
- Van Bladel J. Relativity and Engineering. Vol. 15. Berlin: Springer-Verlag, 1984. 400 p.
- Pastorino M., Raffetto M., Randazzo A. Electromagnetic inverse scattering of axially moving cylindrical targets // IEEE Transactions on Geoscience and Remote Sensing. 2015. Vol. 53, no. 3. P. 1452–1462. DOI: https://doi.org/10.1109/TGRS.2014.2342933
- Zeyde K.M., Sharov V.V., Ronkin M.V. Guided microwaves electromagnetic drag over the sensitivity threshold experimental observation // WSEAS Transactions on Communications. 2019. Vol. 18. P. 191–205.
- Van Bladel J. Electromagnetic fields in the presence of rotating bodies // Proceedings of the IEEE. 1976. Vol. 64, no. 3. P. 301–318. DOI: https://doi.org/10.1109/PROC.1976.10111
- Zeyde K.M. Augmented interpretation model of a moving media for the electrodynamic effects simulation // IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO). 2018. P. 1–4. DOI: https://doi.org/10.1109/NEMO.2018.8503485
- Розанов Н.Н., Сочилин Г.Б. Релятивистские эффекты первого порядка в электродинамике сред с неоднородной скоростью движения // Успехи физических наук. 2006. Т. 176, № 4. С. 421–439. DOI: https://doi.org/10.3367/UFNr.0176.200604f.0421
- Zeyde K.M. The complete form of the propagation constant in a noninertial reference frame for numerical analysis // Zhurnal Radioelektroniki – Journal of Radio Electronics. 2019. № 4. С. 1–15. DOI: https://doi.org/10.30898/1684-1719.2019.4.3
- Zeyde K.M. An Effects set related to the radio signal propagation in a moving reference frame // IEEE 22nd International Conference of Young Professionals in Electron Devices and Materials (EDM). 2021. P. 116–119. DOI: https://doi.org/10.1109/EDM52169.2021.9507609
- Зейде К.М. Дифракция электромагнитных волн на вращающихся осесимметричных телах: дис. … канд. физ.-мат. наук. Воронеж, 2019. 153 с.
- Разработка математической модели кирального метаматериала на основе цилиндрических спиральных элементов с учетом дисперсии и концентрации / И.Ю. Бучнев [и др.] // Физика волновых процессов и радиотехнические системы. 2023. Т. 26, № 2. С. 36–47. DOI: https://doi.org/10.18469/1810-3189.2023.26.2.36-47
- Zarifi D., Soleimani M., Abdolali A. Electromagnetic characterization of biaxial bianisotropic media using the state space approach // IEEE Transactions on Antennas and Propagation. 2014. Vol. 62, no. 3. P. 1538–1542. DOI: https://doi.org/10.1109/TAP.2013.2297166
- Ben-Shimol Y., Censor D. First order propagation in moving chiral media // Proceedings of 19th Convention of Electrical and Electronics Engineers in Israel. 1996. P. 192–195. DOI: https://doi.org/10.1109/EEIS.1996.566927
- Collier J.R., Tai C.T. Propagation of plane waves in lossy moving media // IEEE Transactions on Antennas and Propagation. 1964. Vol. 12, no. 3. P. 375–376. DOI: https://doi.org/10.1109/TAP.1964.1138227
- Zeyde K.M. The coordinate expression of the propagation constant for a moving dielectric medium // Ural Symposium on Biomedical Engineering, Radioelectronics and Information Technology (USBEREIT). 2018. P. 295–298. DOI: https://doi.org/10.1109/USBEREIT.2018.8384608
- Shukla P.K., Singh R.P., Singh R.N. Refractive index of drifting plasma // IEEE Transactions on Antennas and Propagation. 1971. Vol. 19, no. 2. P. 295–296. DOI: https://doi.org/10.1109/TAP.1971.1139924
- Ben-Shimol Y., Censor D. Wave propagation in moving chiral media: Fizeau’s experiment revisited // Radio Science. 1995. Vol. 30, no. 5. P. 1313–1324. DOI: https://doi.org/10.1029/95RS01994
- Caloz C., Sihvola A. Electromagnetic chirality // arXiv. 2019. P. 1–27. URL: https://arxiv.org/abs/1903.09087
- Cheng D.K., Kong J.A. Covariant descriptions of bianisotropic media // Proceedings of the IEEE. 1968. Vol. 56, no. 3. P. 248–251. DOI: https://doi.org/10.1109/PROC.1968.6268
- Zeyde K.M., Hong D., Zhou Yu. Simulation of novel method for material’s weak bianisotropy detection // 3rd International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency (SUMMA). 2021. P. 730–733. DOI: https://doi.org/10.1109/SUMMA53307.2021.9632200
- Бучнев И.Ю., Осипов О.В. Исследование электромагнитных свойств поперечной вставки на основе планарного слоя кирального метаматериала в прямоугольном волноводе // Физика волновых процессов и радиотехнические системы. 2023. Т. 26, № 1. С. 93–105. DOI: https://doi.org/10.18469/1810-3189.2023.26.1.93-105
- Александров Ю.М., Яцышен В.В. Влияние пространственной дисперсии на оптические свойства полупроводников и наноматериалов // Физика волновых процессов и радиотехнические системы. 2017. Т. 20, № 3. С. 60–63. URL: https://journals. ssau.ru/pwp/article/view/7084
- Tsytovich V.N. Spatial dispersion in a relativistic plasma // Journal of Experimental and Theoretical Physics. 1961. Vol. 13, no. 6. P. 1249–1256. URL: http://www.jetp.ras.ru/cgi-bin/e/index/e/13/6/p1249?a=list
- Ryzhov Yu. A., Tamoikin V.V., Tatarskii V.I. Spatial dispersion of inhomogeneous media // Journal of Experimental and Theoretical Physics. 1965. Vol. 21, no. 2. P. 433–438. URL: http://jetp.ras.ru/cgi-bin/e/index/e/21/2/p433?a=list
- Raicu V., Feldman Yu. Dielectric Relaxation in Biological Systems. 1st ed. Oxford: Oxford University Press, 2015. 430 p.
- Causal models of electrically large and lossy dielectric bodies / A. Djordjevic [et al.] // Facta Universitatis. 2014. Vol. 27, no. 2. P. 221–234. DOI: https://doi.org/10.2298/FUEE1402221D
- Джексон Дж. Классическая электродинамика. М.: Мир, 1965. 703 с.
- Dielectric spectroscopy data treatment: I. Frequency domain / N. Axelrod [et al.] // Measurement Science and Technology. 2004. Vol. 15, no. 4. P. 755–764. DOI: https://doi.org/10.1088/0957-0233/15/4/020
- Deck-Léger Z., Zheng X., Caloz C. Electromagnetic wave scattering from a moving medium with stationary interface across the interluminal regime // Photonics. 2021. Vol. 8, no. 202. DOI: https://doi.org/10.3390/photonics8060202
- Скроцкий Г.В. О влиянии силы тяжести на распространение света // Доклады АН СССР. 1957. Т. 114, № 1. С. 73–76.
- Volkov A.M., Izmest’ev A.A., Skrotskii G.V. The propagation of electromagnetic waves in a Riemannian space // Journal of Experimental and Theoretical Physics. 1971. Vol. 32, no. 4. P. 686–689. URL: http://jetp.ras.ru/cgi-bin/e/index/e/32/4/p686?a=list
- Зейде К.М. Применение метода дискретных элементов для изучения рефракционных свойств потока жидкости с мелкодисперсными примесями // Журнал радиоэлектроники. 2018. № 9. С. 1–12. DOI: https://doi.org/10.30898/1684-1719.2018.9.4
- Kong J.A. Charged particles in bianisotropic media // Radio Science. 1971. Vol. 6, no. 11. P. 1015–1019.
- Zeyde K.M. The motion of electrons under the action of inertial forces in the rarefied medium // 3rd URSI Atlantic and Asia Pacific Radio Science Meeting (AT-AP-RASC). 2022. P. 1–4. DOI: https://doi.org/10.23919/AT-AP-RASC54737.2022.9814326
- Zeyde K.M. Fast segmentation of a rotating axisymmetric scatterer medium of an arbitrary form for the first order fields numerical analysis // Ural Radio Engineering Journal. 2018. Vol. 2, no. 2. P. 26–39.
- Saca J.M. Snell’s law for light rays in moving isotropic dielectrics // Proceedings of the IEEE. 1980. Vol. 68, no. 3. P. 409–410. DOI: https://doi.org/10.1109/PROC.1980.11649


