Взаимодействие частиц в неоднородном магнитном поле
Автор: Борискина И.П.
Журнал: Инженерные технологии и системы @vestnik-mrsu
Рубрика: Физико-математические науки
Статья в выпуске: 3-4, 2003 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/14718513
IDR: 14718513
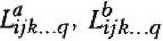
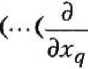
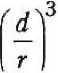
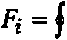
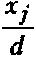
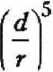
Список литературы Взаимодействие частиц в неоднородном магнитном поле
- Мартынов С. И. Взаимодействие частиц в суспензии. Казань: Изд-во Казан, мат. о-ва, 1998. 135 с.
- Мартынов С. И. Взаимодействие частиц в течении с параболическим профилем скорости//Изв. РАН. Механика жидкости и газа. 2000. Me 1. С. 84 -91.
- Мартынов С. И. Гидродинамическое взаимодействие частиц//Изв. РАН. Механика жидкости и газа. 1998. № 2. С. 112 -119.
Статья
