Взаимодействие гусеничной машины с препятствием

• -    тундра, лесотундра и подтаежная зона;

• -    лесная таежная зона;

• -    зона горных лесов.

Цель исследований . Разработать классификацию лесных препятствий и исследовать взаимодействие пораметров двухгусеничной машины на вертикальную стенку подъёма.

Объект и методы исследований . Двухгусеничная машина, принятые допущения, исследование преодоления лесных препятствий.

В зависимости от преимущественных условий эксплуатации лесная машина может быть выполнена горной, болотоходной, плавающей, а также предназначенной для работы в равниннохолмистой местности. Каждая из модификаций лесной машины, предназначенная для функционирования в определённых зонах, должна иметь соответствующие конструктивные особенности, позволяющие ей безопасно выполнять необходимые технологические операции и иметь достаточно высокую проходимость, позволяющую преодолевать встречающиеся препятствия [1].

К характерным условиям функционирования лесной техники во всех трёх зонах относится пересеченная местность, представляющая собой совокупность различных препятствий естественного и искусственного происхождения, ориентированных в различных направлениях и расположенных в случайном порядке.

Препятствия, которые могут быть встречены лесной машиной, могут быть в виде неровностей опорной поверхности (бугры, ямы искусственного и естественного происхождения, овраги), а также в виде пней, поваленных деревьев, камней, кочек и др. Возможная классификация лесных препятствий применительно к указанным трём зонам представлена на рисунке 1.

Одним из препятствий, которые можно встретить во всех трёх зонах, является пороговое препятствие, имеющее в наиболее сложных случаях вертикальную стенку. Частными случаями порогового препятствия являются бугры, кочки, валёжины и т.д. Они не представляют особой трудности для их преодоления, поскольку характеризуются достаточно плавными изменениями углов наклона опорной поверхности к горизонту.

Теоретические исследования возможности преодоления пороговых препятствий проводились как для отдельного колеса, так и для машины в целом.

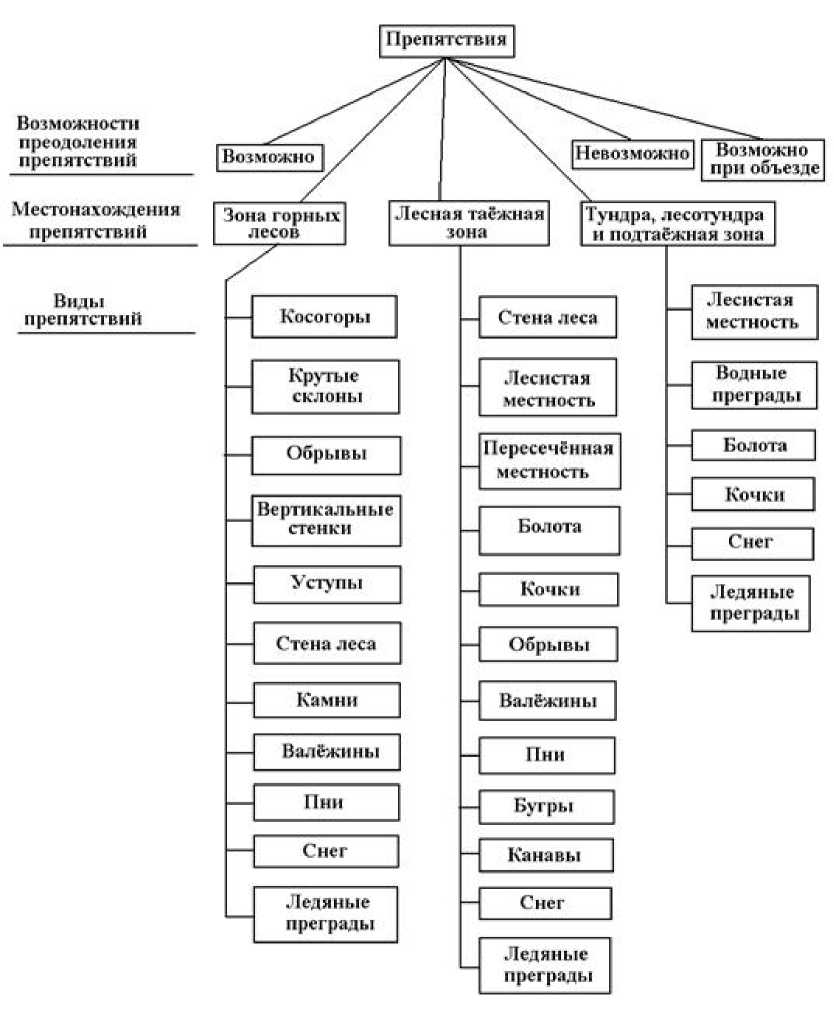
Рис. 1. Классификация лесных препятствий

Изучалось преодоление порогового препятствия неведущим колесом, ведущим колесом, жёстким и эластичным колесом и т.д. При проведении этих исследований полагалось, что колесо и машина находятся на горизонтальной площадке. Было показано, что высота преодолеваемого порогового препятствия зависит от того, ведущее колесо, или ведомое, от того, каков радиус колеса, имеется ли дополнительно приложенная к оси колеса толкающая сила.

Теоретических исследований преодоления пороговых препятствий гусеничной машиной в открытой печати обнаружить не удалось. В известных источниках информации [2–5 и др.] отмечалась лишь технология преодоления такого препятствия, а также рассуждения о влиянии на высоту преодолеваемого порогового препятствия различных конструктивных параметров гусеничной машины и характеристик опорной поверхности. В [5] приведена формула для определения высоты преодолеваемого порогового препятствия танком hэ

2 A - Б

где   А – полная длина танка (без пушки);

Б – полная высота танка.

Формула составлена в предположении, что центр тяжести находится посередине длины танка и отстоит от земли на 0,4 его полной высоты, а сцепление гусениц с гребнем эскарпа достаточное.

Таким образом, конкретное влияние конструктивных параметров машины и связи её гусениц с опорной поверхностью в известных исследованиях не определено.

Определим возможность подъёма двухгусеничной машины на вертикальную стенку. Примем следующие допущения: двухгусеничная машина имеет ведущую звёздочку и натяжной каток, являющиеся одновременно и опорными катками (рис. 2).

Вертикальная стенка

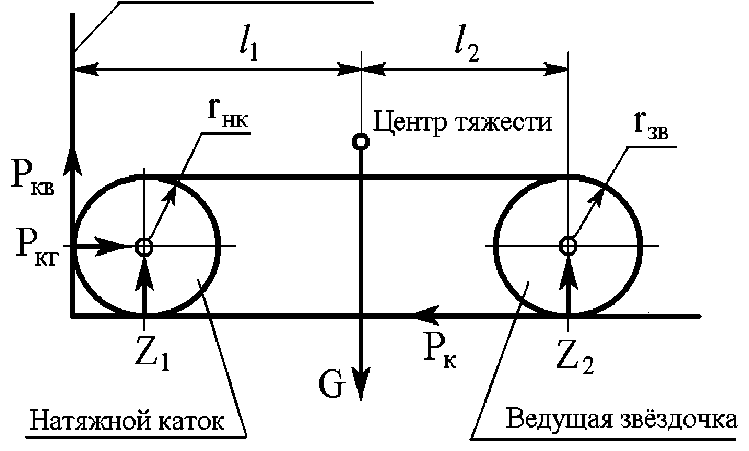
Рис. 2. Схема взаимодействия гусениц двухгусеничной машины с вертикальной стенкой

Составим уравнения равновесия машины.

Сумма моментов действующих сил относительно оси ведущей звёздочки

Ркв (11 + 12 ) + Z1 (l1 + 12 - Гк ) + Ркг (Гк — r.. ) + Рк Гзв — Gl2 = 0.   (2)

Сумма проекций действующих сил на вертикальную ось

Р кв + Z 1 + Z 2 - G = 0 .                           (3)

Сумма проекций на горизонтальную ось

(4) к      кг       .

В этих уравнениях:

сила сцепления гусеницы с вертикальной стенкой;

кв

Z i — нормальная реакция опорной поверхности на натяжной каток;

Z 2 — нормальная реакция опорной поверхности на ведущую звёздочку;

• нормальная реакция вертикальной стенки на натяжной каток;

кг

• тяговое усилие гусеницы относительно опорной поверхности;

к

G — вес машины.

Кроме вышеуказанных, имеют место следующие уравнения:

Р к = Z 2 ф г ;  Р кв = I- ф в ,                         (5)

где % - коэффициент сцепления гусеницы с горизонтальной опорной поверхностью;

• % - коэффициент сцепления гусеницы с вертикальной стенкой.

Начало подъёма машины на вертикальную стенку характеризуется нулевым значением нормальной реакции опорной поверхности на натяжной каток. Уравнение (2) принимает тогда следующий вид:

Ре (li +12 ) + P(r^ — Г в) + Рк r, — Gl2 = 0, кв                кг нк    зв       к зв а уравнение (3)

Ркв + Z2 - G = 0.

С учётом уравнений (4), (5), (7) уравнение (6) после преобразований принимает следующий вид:

l2

Ф в ^{( l} 1 ^{+ 1} 2 ^{)+ Г}нк ^— Ф e^l 2 = ⁰ .

Ф г

Пусть rm = ГзвКнк, где к,. = нК - коэффициент, определяющий соотношение радиусов натяжного катка к. и веду-зв щей звёздочки rзв гусеницы. Тогда l                             (10)

Ф в ^{( l}1 + ¹ 2 ^{)+ Г}зв^Кнк -Ф в¹ 2 = ⁰ ,

Ф г или

ФвФгl1 + ГзвКнкФг - 12 = 0•                 (11)

Коэффициент сцепления гусеницы относительно вертикальной стенки в общем случае не равен коэффициенту сцепления гусеницы с горизонтальной опорной поверхностью. Введём коэффициент      , определяющий соотношение коэффициентов сцепления относительно вертикальной ср стенки и горизонтальной опорной поверхности.

к       ^Ф' в ;

ср Фг '

Ф в = ^Кср Ф г •

Подставим значение коэффициента сцепления относительно вертикальной стенки из (12) в (11).

К сvk Фг + Г₃ КнФг - ^ = 0 • ср 1 г     зв нк г     2

Решим уравнение (13) и определим минимальное значение коэффициента сцепления относительно горизонтальной поверхности, при котором возможен подъём передней части гусеничной машины на вертикальную стенку. Поскольку коэффициент сцепления не может быть отрицательным, решение уравнения имеет вид

Ф г

- ^Гзв^Кнк + 4^Гзв^КНк + ^{4 К}ср^l1¹ 2

2 к _ср l ₁

Разделим числитель и знаменатель на l 1 и получим безразмерное уравнение, определяющее минимальное значение коэффициента сцепления гусеницы с горизонтальной опорной поверхностью, обеспечивающее подъём натяжного катка на вертикальную стенку.

—

Ф г

ГКнк +л !^Гз ² к 2_К + 4 К_с l ₂ , зв нк       зв нк        ср ,

2 к ср

здесь

Г зв

^r зв           ^l 2

I ’ 12 = I • l1                l1

Если коэффициенты к и к равны единице, то

Ф_г = - 0 ,5r„ + 7 0 . 25 r 2 + 4 . г           зв             зв 2

Проанализируем уравнение (15).

График, представленный на рисунке 3 и построенный при к ср = [0,5; 1,0; 1,5], Г зв = 0,1, показывает, что минимально необходимый для подъёма на вертикальную стенку передней части гусеницы (натяжного катка) коэффициент сцепления гусеницы с горизонтальной поверхностью уменьшается при уменьшении отношения расстояния от центра тяжести гусеничной машины до оси ведущей звёздочки к расстоянию от центра тяжести машины до оси натяжного катка. Другими словами, чем ближе расположен центр тяжести машины к оси ведущей звёздочки, тем минимально необходимый коэффициент сцепления гусеницы с горизонтальной поверхностью будет меньше. Необходимый коэффициент сцепления уменьшается и при увеличении радиуса натяжного катка в сравнении с радиусом ведущей звёздочки, другими словами, с увеличением расстояния от оси натяжного катка до горизонтальной опорной поверхности.

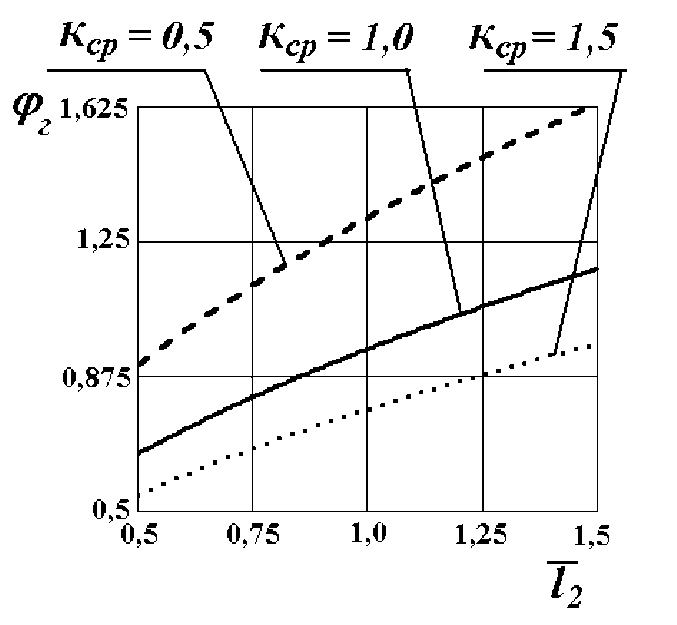
Рис. 3. Зависимости минимального значения коэффициента сцепления гусеничной машины с горизонтальной поверхностью

График, приведенный на рисунке 4 и построенный при к нк = [0,5; 1,0; 1,5], Г зв = 0,1 показывает, что минимально необходимый для подъёма на вертикальную стенку передней части гусеницы (натяжного катка) коэффициент сцепления гусеницы с горизонтальной поверхностью существенно зависит от соотношения коэффициентов сцепления гусеницы с горизонтальной и вертикальной поверхностями. Чем больше коэффициент сцепления гусеницы с вертикальной стенкой к ср > 1, тем минимально необходимый для подъёма на вертикальную стенку натяжного катка коэффициент сцепления с горизонтальной поверхностью будет меньше.

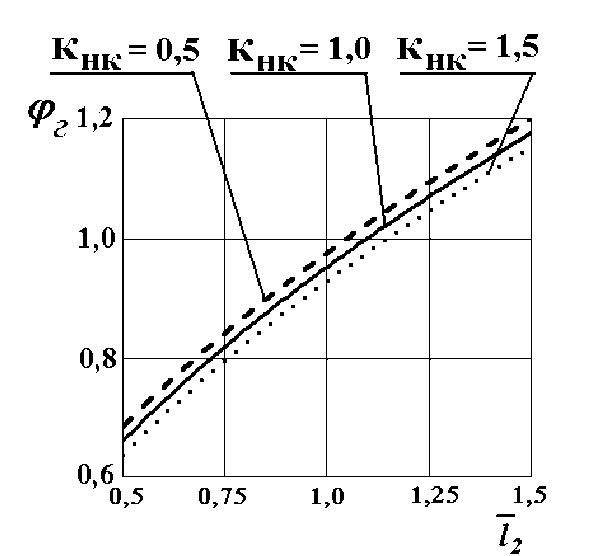
Рис. 4. Зависимости минимального значения коэффициента сцепления гусеничной машины с горизонтальной поверхностью

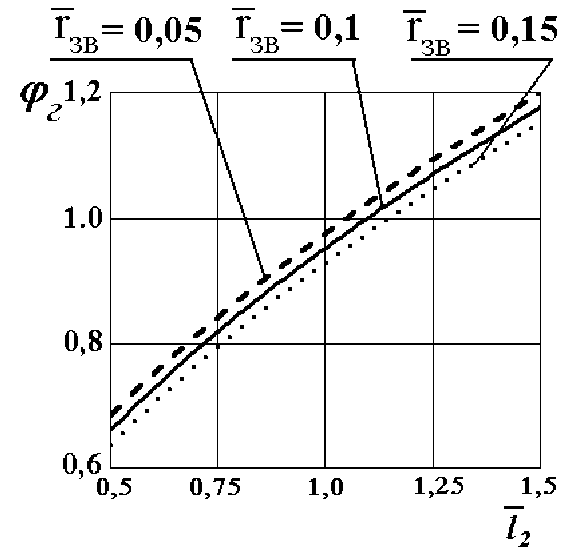
Рис. 5. Зависимости минимального значения коэффициента сцепления гусеничной машины с горизонтальной поверхностью

График, приведенный на рисунке 5 и построенный при Г зв = [0,05; 0,1; 0,15],к ср = 1, к нк = 1 , показывает, что уменьшение минимально необходимого коэффициента сцепления гусеницы с горизонтальной поверхностью обеспечивает увеличение радиуса ведущей звёздочки.

Выводы. С подъёмом передней части гусеничной машины на вертикальную стенку увеличивается угол наклона машины, при этом уменьшаются необходимые для этого подъёма тяговые усилия гусениц.

При определённых конструктивных параметрах гусеничной машины и реальных коэффициентах сцепления гусениц подъём на вертикальную стенку передней части гусениц возможен.