Взаимодействие некоаксиальных цилиндрических поверхностей через заполненный жидкостью зазор между ними

Электронный журнал «Техническая акустика»

Для повышения виброизоляции источника низкочастотных динамических сил могут быть использованы виброизолирующие системы [1, 2], в которых, помимо традиционного упругого (характеризуемого жесткостью C ) канала связи источника вибрации с опорной конструкцией, организуется дополнительный, параллельный первому, инерционный канал, как показано на рис. 1а. На этом рисунке обозначено: £ — амплитуда колебательного смещения источника вибрации, а — круговая частота колебаний, m c — коэффициент с размерностью массы (масса связи); F y , F u — динамические силы, передающиеся соответственно по упругому и инерционному каналам, F o — переменная сила, действующая на опорную конструкцию, равная F o = F y + F_u .

Исследования показали, что такая система виброизоляции действительно обладает повышенной эффективностью в области низких частот по сравнению с традиционной амортизацией, если основной частью ее инерционного канала является жидкостный элемент. В этом случае виброизолирующую систему будем называть упругожидкостной (УЖВИС). Устройство такой системы базируется на принципиальной схеме, предложенной в работе [3]. Жидкостный элемент обеспечивает инерционный характер взаимодействия виброактивного источника с его опорной конструкцией в широком диапазоне низких частот [4]. При этом динамическая связь осуществляется через заполненные жидкостью зазоры между отдельными частями жидкостного элемента.

Вид частотной характеристики эффективности виброизоляции УЖВИС показан на рис. 1б. Представленная кривая имеет максимум в области низких частот. Положение на частотной шкале этого максимума при фиксированной жесткости C зависит от степени передачи динамических сил по инерционному каналу, которая численно определяется величиной массы динамической связи m_c .

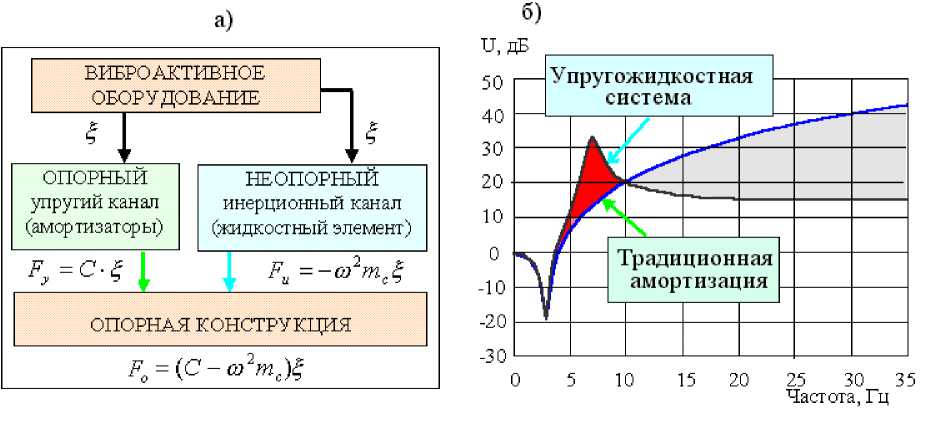
Рис. 1. Принципиальная схема (а) и пример частотной характеристики эффективности виброизоляции (б) упругожидкостной виброизолирующей системы

Рассмотрим возможность конструктивного исполнения жидкостного элемента УЖВИС в виде заполненного жидкостью зазора, ограниченного двумя, в общем случае некоаксиальными, цилиндрическими поверхностями. Схема такого элемента представлена на рис. 2. Внешняя цилиндрическая поверхность радиуса R жестко связана с опорной конструкцией, а внутренняя, радиуса r0 , связана с источником вибрации и совершает осциллирующие колебания по закону υ =υ0 cos(ϕ1 -α). Здесь υ0 — амплитуда скорости осцилляции колеблющейся поверхности, а ϕ1 — угловая координата в связанной с ней цилиндрической координатной системе (r1,ϕ1,z ). Ось внешней неподвижной цилиндрической границы смещена относительно оси внутренней на величину δ , причем угол между направлением колебаний внутренней поверхности и направлением указанного смещения осей равен α. Зазор между цилиндрическими границами заполнен жидкостью. Для удобства решения задачи введем также и вторую систему координат, ось которой совпадает с осью симметрии внешней границы — (r2,ϕ2,z ).

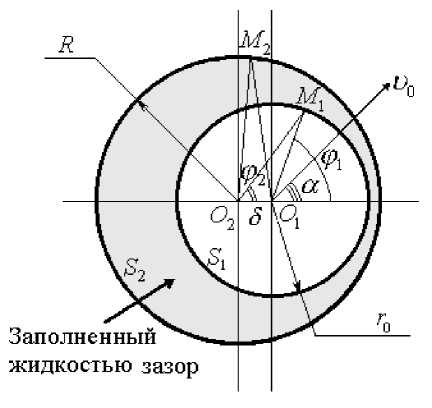
Рис. 2. Схема жидкостного элемента с цилиндрическими границами

• 2.    РАСЧЕТНЫЕ СООТНОШЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ДИНАМИЧЕСКИХ

ХАРАКТЕРИСТИК ЖИДКОСТНОГО ЭЛЕМЕНТА

Если динамическое взаимодействие между неподвижной и колеблющейся границами носит инерционный характер, то это взаимодействие можно описать погонной массой динамической связи погонной силы F , действующей со неподвижную границу, к амплитуде

m_c . Эту массу определим как отношение стороны заполняющей зазор жидкости на ускорения колеблющейся цилиндрической

поверхности в плоскости ее осцилляции, т. е.

m_c = F / j ωυ ₀ ,

в

Чтобы определить указанную силу, нужно найти звуковое давление p заполненном жидкостью зазоре. Тогда искомая сила F определится соотношением F = ∫ p cos( ϕ ₂ - α ) dS ₂ ,

S 2

где ϕ ₂ — угловая координата в цилиндрической системе координат, ось z которой совпадает с осью симметрии поверхности S ₂ (см. рис. 2).

Звуковое давление связано с потенциалом жидкости в зазоре Φ , который, в свою очередь, может быть определен из решения уравнения Гельмгольца

∆Φ - k ² Φ = 0,

где k — волновое число, с соответствующими граничными условиями

∂ Φ

∂ r 1 _S

= υ ₀ cos( ϕ ₁ - α ) ,

ЭФ

Э r ₂

= 0,

S 2

где r1 и r2 радиальные координаты в системах координат, связанных с внутренней и внешней границами соответственно. Таким образом, оказывается, что граничные условия (4) и (5) записаны в различных координатных системах. Будем искать решение поставленной задачи в виде

Ф = Ф 1 + Ф ₂,

где

ж

Ф 1 = A 0 ¹ ) J о⁽ kr i ) + Х J_n ⁽ kr i )( A n ¹’cos ф + B ^sin П 9 1 ),                                 (7)

n = 1

ж

Ф 2 = A 0 ²⁾ N 0^{( kr}2 ) + 1 Nn ^{( k} r 2⁾⁽ A n ²⁾c ^os П ф 2 + ^ П ²⁾ sin ⁿ $ 2 ). (8) n = i

Здесь J_n ( kr₁ ), N_n ( kr ₂) — функции Бесселя и Неймана порядка n от аргументов kr₁ , kr₂. Очевидно, что функции Ф 1 и Ф ₂ также, как и граничные условия, записаны в разных системах координат.

Для того чтобы удовлетворить граничному условию (4), нужно выразить функцию Ф ₂ в системе координат ( r 1 , ф ₁ ) . Это можно сделать, применив теоремы сложения цилиндрических функций [5] к треугольнику O ₂ M ₂ O ₁ . Аналогично, чтобы удовлетворить условию (5), выразим функцию Ф 1 в координатах ( г₂, ф 2 ) , воспользовавшись теоремами сложения для треугольника O ₁ O ₂ M ₁ . Приравнивая коэффициенты при sin п ф и cos п ф в правой и левой частях полученных равенств, приходим к бесконечной системе уравнений для нахождения неизвестных коэффициентов A_n ^{(1), (2)} , B_n ^(1),(2) , которую можно решить численно, ограничившись некоторым числом неизвестных N . В результате выражение для звукового давления в зазоре примет вид

Р = Р1 + Р 2, где

Р 1 = j o>P

N

A 0 ¹ ) J 0 ( kr ) + ^ J_n ( kr )( A n ¹’ cos П Ф 1 + В П ¹’ sin П Ф 1 ) n = 1

-N p2

= j ap A 0 ) N o ( kr 2 ) + ^ N n ( kr) ⁽ A ) cos п ф 2 + В П ) sin п ф 2 ) .

n = 1

Подставим данное выражение в соотношение (2), представив с помощью теорем сложения функцию p 1 в координатах r2, ф2, и вычислим интеграл. В результате для нахождения погонной массы связи (1) рассматриваемого жидкостного элемента получим следующее соотношение mc = -^ ‘ {2 A01 J1 (kR) ‘ J1 (kS) cosa + N1 (kR)(A^2) cosa + B1(2) sin a)

^u 0

■^l1 (kR) - (-1) n [An" (J,+1 (kS) - An-(kS ))cosa - B"'(J,+1 (kS)+J,,-1 (kS ))sin a J n =1

Если у рассматриваемого жидкостного элемента внешняя поверхность связана с источником вибрации и колеблется, а внутренняя, наоборот, жестко связана с опорной конструкцией и может считаться неподвижной, то для вычисления массы связи также можно использовать формулу (9), но со знаком “минус”, т.к. направление внешней нормали к колеблющейся поверхности в данном случае меняется на противоположное.

Если жидкостный элемент состоит из двух или более несообщающихся между собой зазоров, то его масса связи равна сумме масс связи каждого из зазоров, которые также могут быть рассчитаны по формуле (9).

В случае коаксиальных цилиндрических поверхностей ( S = 0 ) и при kR <<  1 формула для массы связи может быть представлена в виде

т c Is=0, kR <<1

= ⁿ Pr \

R ²

-

² r ₀

2 R ²

-

k ² r ₀ ²

. R 3 (R² ln--h —

r ₀

4 ^ r o ²

-

R!

Al

- 1

• 3.    ИССЛЕДОВАНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

Поскольку на практике при изготовлении жидкостного элемента или в процессе его эксплуатации может возникнуть некоаксиальность ограничивающих его поверхностей, далее основное внимание будет уделено влиянию на величину массы связи этого фактора.

На рис. 3а приведена зависимость отношения массы динамической связи, обеспечиваемой жидкостным элементом (mc ), схема которого показана на рис. 2, к массе связи жидкостного элемента с коаксиальными границами тех же радиусов (mc0 ) от относительного смещения оси активного цилиндра S/ R . Расчет выполнен для отношения радиусов внутренней и внешней границ r0 / R = 0,8 и частотного параметра kr0 = 0,2 для двух различных направлений колебаний. Из представленных на рисунке данных следует, что масса связи возрастает с ростом относительного смещения осей. При этом она слабо зависит от направления колебаний внутренней границы. Максимальное значение отношения S/R , представленное на графике, равно (S/R L. = 1 - 41R = 0,2, что соответствует случаю касания внешней и внутренней цилиндрических границ. Однако при практическом использовании жидкостного элемента в УЖВИС следует ограничиться меньшим значением рассматриваемого отношения, чтобы исключить возможность соударений элементов системы. Если минимально допустимое расстояние между границами в соответствии с этим требованием составляет 81 = 0,05R, то максимально возможное значение относительного смещения осей в данном случае будет равно (8/ R )max = 1 - 41R - 81,R = 0,15. При этом максимальное значение массы связи при заданном соотношении радиусов составит примерно 1,2 mc0 . Расчеты показывают, что аналогичные результаты получаются и при других соотношениях радиусов границ.

а)

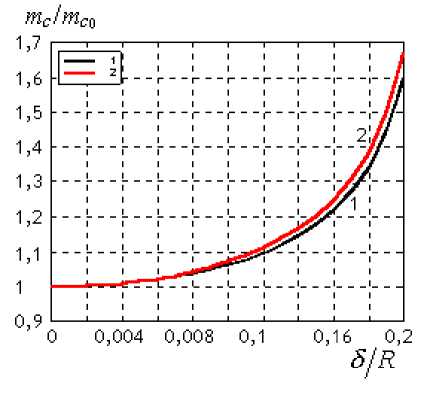
Рис. 3. Зависимости отношения mjm^

а) от относительного смещения оси 8 / R для различных направлений колебаний ( а ) при r ₀ / R = 0,8 ; kr ₀ = 0,2: 1 — а = 0; 2 — а = л/ 2;

б) от угла а при смещении оси 8 / R = 0,8 -(8 / R ) _max и kr₀ = 0,2 для различных r ₀ /R : 1 — r ₀/ R = 0,7; 2 — r ₀ / R = 0,8; 3 — r ₀ / R = 0,9

б)

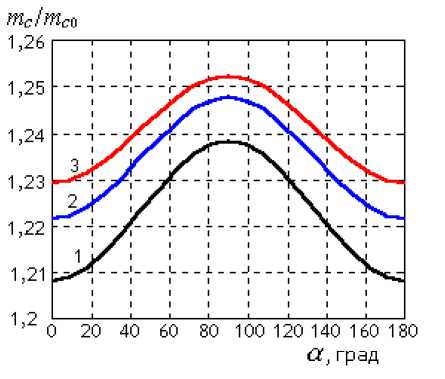
На рис. 3б приведены зависимости массы динамической связи от угла между направлением колебаний активного цилиндра и направлением смещения его оси при различных значениях отношения радиусов цилиндрических границ жидкостного элемента r ₀ R . Здесь масса динамической связи, как и далее, на рис. 4а, нормирована ее значением для жидкостного элемента с коаксиальными границами того же радиуса. Расчет выполнен для одного значения частотного параметра kr₀ = 0,2 при постоянной величине смещения осей 8/R = 0,8 ( 8/R ) _max. По материалам рисунка видно, что масса связи достигает максимального значения при а = л/ 2, т. е. при колебаниях внутренней границы зазора в направлении, перпендикулярном направлению смещения оси. Зависимость от угла а выражена тем сильнее, чем ближе отношение r₀ /R к 1, но даже для достаточно узких зазоров при выбранном значении частотного параметра kr ₀ = 0,2

влияние направления колебаний на величину массы связи можно считать незначительным.

На рис. 4а представлена поверхность, отражающая зависимость отношения m_c m_{c 0} от частотного параметра kr ₀ и направления колебаний внутренней границы жидкостного элемента.

б)

а)

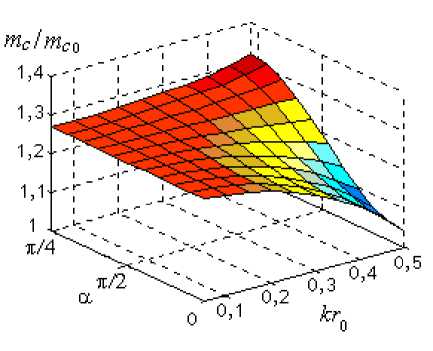
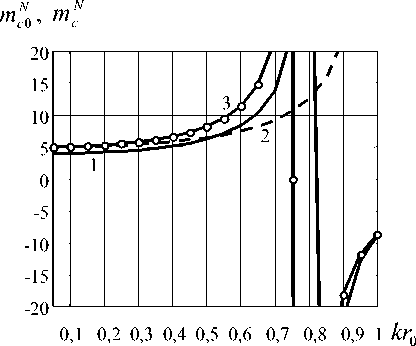
Рис. 4. Зависимость отношения т _& /т^ от частотного параметра kr₀ и угла а (а) и масс связи m_c^N ₀ , m_c^N от kr ₀ (б) при различных значениях α ( r ₀ / R = 0,7) 1 — δ / R = 0; 2 — α = 0, δ / R = 0,25; 3 — α = π /2, δ / R = 0,25

Видно, что в области низких частот, при малых значениях частотного параметра kr ₀ , масса связи практически не зависит от направления колебаний осциллирующей границы, однако с ростом частоты эта зависимость начинает проявляться сильнее. При этом с изменением угла α от 0 до π /2 меняется характер зависимости отношения m_c m_{c 0} от частоты: при α = 0 величина m_c m_{c 0} с ростом частоты уменьшается, а при α = π /2 , наоборот, увеличивается. Такое поведение рассматриваемого параметра поясняется материалами рис. 4б, на котором представлены частотные зависимости погонных, нормированных величиной πρ r ₀² , значений масс m_c^N ₀ (не зависит от α ) и m_c^N (является функцией угла α ) при различных значениях этого угла. Все представленные на рисунке кривые ведут себя примерно одинаково: на низких частотах масса связи остается практически постоянной, затем с ростом частоты она возрастает вплоть до некоторой критической частоты ( kr ₀) _kr . При kr ₀ = ( kr ₀) _kr инерционная реакция жидкостного элемента на колебания поверхности меняется на упругую и масса связи становится отрицательной.

На низких частотах масса связи жидкостного элемента с некоаксиальными границами практически не зависит от направления колебаний и всегда превышает массу связи элемента, ограниченного коаксиальными цилиндрическими поверхностями. С ростом значений параметра kr 0 при а = 0 масса связи жидкостного элемента с некоаксиальными границами растет медленнее массы mc0 и, начиная с некоторой частоты, становится меньше ее. В результате отношение mc mc0 уменьшается и при близких к критическому значениях kr 0 стремится к 0. При а = л/ 2 масса связи жидкостного элемента с некоаксиальными границами растет быстрее, чем mc , поэтому отношение mc mc0 с ростом частоты увеличивается вплоть до критической частоты (kr0)kr .

Таким образом, существенное различие между значениями массы связи m_c и m_{c 0} могут быть получены только при довольно высоких, близких к критическому, значениях частотного параметра. Однако в этом частотном диапазоне применение УЖВИС нецелесообразно из-за резкого снижения их эффективности. В области же низких частот, где упругожидкостные системы обладают повышенной эффективностью по сравнению с классическими, некоаксиальность ограничивающих жидкостный элемент цилиндрических поверхностей мало влияет на величину обеспечиваемой им массы связи.

Все приведенные выше результаты расчетов относятся к случаю осцилляций внутренней границы зазора. Аналогичные результаты получаются и для случая колебаний его внешней границы.

• 4.    ВЛИЯНИЕ НЕКОАКСИАЛЬНОСТИ ГРАНИЦ НА ЭФФЕКТИВНОСТЬ УЖВИС В ЦЕЛОМ.

Эффективность простейшей однокаскадной УЖВИС, принципиальная схема которой показана на рис. 1a, может быть вычислена по формуле

U = 20lg

1 - v²

1 - цу²

где у = f / fa — безразмерная частота, f = т /2л , f = — —

J a 2л} IM

C

— частота амортизации,

+ m c

C — жесткость упругого канала, M — масса виброактивного оборудования, m_c — масса связи, обеспечиваемая жидкостным элементом, ц = m c (( M + m c ) — коэффициент связи по инерционному каналу.

На низких частотах массу связи можно считать постоянной и равной ее значению при kr₀ = 0.

Характеристика эффективности виброизоляции в области низких ча стот имеет минимум на частоте амортизации и максимум на частоте f _max = 1 / 2 π C / m_c или ν max ^{= 1 µ .}

Как было показано в предыдущей части, максимально возможное увеличение массы связи жидкостного элемента путем смещения оси одной из его границ составляет примерно 20% . Если коэффициент связи µ жидкостного элемента с коаксиальными границами был равен 0,2, то такое изменение массы связи вызовет его увеличение до 0,23 . Это в свою очередь приведет к уменьшению максимума эффективности примерно на 2 дБ и снижению его частоты на 9%, как показано на рис. 5.

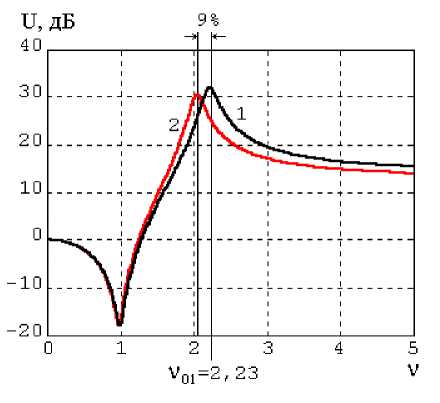
Рис. 5. Изменение частотной характеристики эффективности виброизоляции УЖВИС под влиянием смещения осей ограничивающих жидкостный элемент цилиндрических поверхностей

• 1    — δ = 0, m_c = m_{c 0}, µ = 0,2;

• 2    — δ = δ _max, m_c = 1,2 ⋅ m_{c 0}

Таким образом, несовпадение осей цилиндрических поверхностей жидкостного элемента рассматриваемого типа, исключающее возможность соударений взаимодействующих через жидкость поверхностей, не оказывает существенного влияния на эффективность виброизоляции УЖВИС вследствие малого изменения массы связи. По этой же причине использовать смещение оси для настройки упругожидкостной системы с целью адаптации ее частотной характеристики к спектру источника нецелесообразно. Даже при максимально возможном смещении оси (кривая 2), на частоте ν = ν ₀₁ = 2,23, соответствующей положению максимума эффективности системы с коаксиальными границами (кривая 1), эффективность остается достаточно высокой, а наиболее вероятные малые смещения оси δ / R ≤ 0,05 вообще не вызовут заметных изменений частотной характеристики эффективности системы.

ЗАКЛЮЧЕНИЕ

В результате выполненных расчетов установлено, что малые смещения осей цилиндрических границ жидкостного элемента, которые могут возникнуть при его изготовлении или в процессе эксплуатации виброизолирующей системы, не оказывают заметного влияния на частотную характеристику эффективности виброизоляции. Это связано с тем, что путем смещения оси одной из ограничивающих жидкостный элемент цилиндрических поверхностей невозможно добиться существенного изменения обеспечиваемой им массы связи. По этой же причине этот путь нецелесообразно использовать для управления частотной характеристикой эффективности виброизоляции упругожидкостной системы.