Взаимодействие сферических ударных волн с приповерхностным гетерогенным слоем с химически активной газовой фазой

Интерес к изучению взаимодействия ударных волн (УВ) с механическими и тепловыми неоднородностями связан с анализом возможности применения взрыва в борьбе с природными и техногенными катастрофами. Успешное применение быстропротека-ющих процессов в борьбе с лесными пожарами дало возможность построить ряд математических моделей [1, 2], которые позволили выявить некоторые особенности при взаимодействии УВ с фронтом лесного пожара. Полученные закономерности в полной мере применимы к анализу последствий взаимодействия космических объектов с поверхностью Земли. В связи с тем, что в последнее время увеличилось количество крупных метеоритов, упавших на нашу планету, возникает интерес к математическому моделированию данных явлений [3-9] с учетом всего многообразия присущих данному явлению факторов.

Входя в плотные слои атмосферы космическое тело испытывает резкое торможение, в ударном слое создается высокое давление (порядка тысячи атмосфер), что приводит к образованию больших лучистых и тепловых потоков. Под действием высоких механических и термических напряжений происходит разрушение тела, (как частичное, так и полное) с выделением энергии. В результате этого образуются ударные волны, которые оказывают разрушающее воздействие на наземные объекты, а. часть энергии в виде излучения может привести к возникновению пожаров.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Целью данной работы является исследование влияния возможного химического превращения газообразных продуктов пиролиза лесных горючих материалов в приповерхностном слое на параметры падающей ударной волны.

1.    Постановка задачи

Рассмотрим модельную задачу о взаимодействии сферической УВ с гетерогенным слоем на поверхности Земли, заполненным газообразными продуктами пиролиза. Пусть к некоторому моменту времени в атмосфере на некоторой высоте над поверхностью Земли образовался сферический объем сжатого горячего газа, все параметры внутри этого объема распределены равномерно. Данный объем образовался в результате взрыва в атмосфере Земли, например, некоторого космического тела. При сильном атмосферном взрыве на начальном этапе развития процесса значительную роль может играть излучение, однако в рассматриваемой постановке задачи влиянием излучения пренебрегается. Это объясняется тем, что в рассматриваемой задаче « высвечивание » области энерговыделения уже произошло, и к моменту формирования объема постоянного давления роль излучения несущественна [3]. К поверхности Земли прилегает гетерогенный слой высотой H. Такой слой в данной постановке имитирует лесной массив. Газовая фаза в этом слое представляет продукты пиролиза лесных горючих материалов, образованные от воздействия излучения (вспышки) на лесной массив.

В результате разлета объема сжатого газа формируется сферическая ударная волна, которая взаимодействует с гетерогенным слоем и инициирует в нем химические превращения.

Расчетная область (рис. 1) ограничена слева осью Oz цилиндрической системы координат, которая является осью симметрии. Снизу твердой поверхностью (ось Or цилиндрической системы координат). Верхняя граница также является осью симметрии. Численные расчеты поэтому проводились до моментов времени, пока отраженная от нижней стенки ударная волна не достигла верхней границы. Правая граница области - свободная граница.

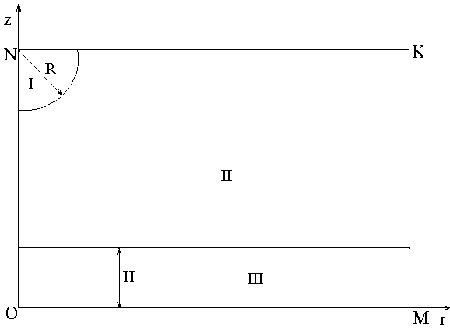
Рис. 1. Схема расчетной области в начальный момент времени

В качестве математической модели гетерогенного слоя рассматривается математическая модель « замороженной » газовзвеси, т.е. недеформированная решетка, заполненная газом [10-12]. Твердые частицы имитируют ее узлы, влиянием связей ре

Н.Л. Клиначева, Ю.М. Ковалев шеток пренебрегаем. Анализ инвариантности относительно преобразования Галилея и возможности использования математической модели «замороженной» газовзвеси был проведен в работах [12, 13].

Математическая модель изучаемого физического процесса представляет собой систему дифференциальных уравнений Эйлера для двумерного осесимметричного нестационарного движения газа в цилиндрических координатах в области чистого газа и модели « замороженной » газовзвеси в области гетерогенного слоя. Система замыкается уравнениями состояния фаз [14] и условиями межфазного взаимодействия [15, 16]:

∂t ∂r         ∂z д (р 1 и 1 r)    д (р 1 и 1 и 1 r)    д (р 1 и 1 v 1 r)            д (ra 1 P)

rF _r α ₁

z

∂t

∂t

Q

∂z

W 2

rQα 1 ,

P

ρ ⁰₁( γ - 1)

E 1 = e 1 +

= 0

^W 1²

2,

_ρ 0_{2 ρ} 0₁

const

где r и z - радиальная и осевая координаты; t - время, и и v - компоненты вектора скорости W; P - давление; e 1, E 1, р ⁰ - удельная внутренняя и полная энергии газа, истинная плотность; y ~ показатель адиабаты газа; a 2 - объемная доля частиц; c _p - удельная теплоемкость при постоянном давлении твердой фазы; F и Q - интенсивности силового и теплового взаимодействия газа с узлами решетки. Уравнения, определяющие силовое и тепловое взаимодействие газа и частиц, аналогичны уравнениям [15, 16]:

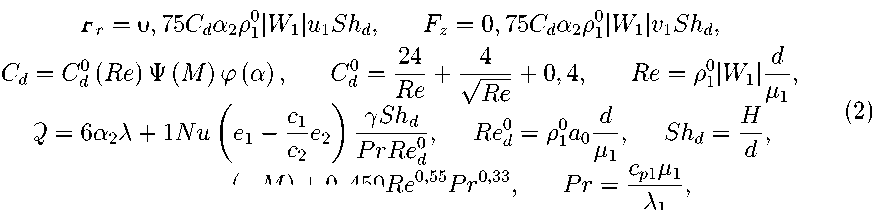
F r = 0 , 75 C d a 2 р 1 |Ж 1 |и i Sh d ,    F z = 0 , 75 C _d a 2 р 0 |Ж 1 |v 1 Sh _d

Re = р 1 |Ж 1 | d,

Re

+      + 0 , 4

Re

C d = C d ( Re ) Ф ( M ) ф ( a ) ,    C d

0 ^d

Re ⁰ d

P rRe0d cp1µ1

λ 1

Nu = 2 exp ( —M ) + 0 , 459 Re ¹ ’ ⁵⁵ Pr ¹ ’ ³³

где C_d - коэффициент аэродинамического сопротивления сферы; C d - коэффициент аэродинамического сопротивления частиц в несжимаемом безграничном потоке газа; М, Re, Nu и Pr - числа Маха, Рейнольдса, Нуссельта и Прандтля; d - диаметр частиц: А ₁. ц ₁. щ - теплопроводность, вязкость п местная скорость звука, газа: а₀ - характерная скорость звука в невозмущенном газе.

Уравнения, описывающие химическую кинетику протекающих процессов в гете-

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ рогенном слое, имеют вид:

д ( р i C i r ) ∂t

+ д ( р i u i C i r ) + д ( р i v i C i r )

∂r          ∂z

J = 52 q j s j ,

= rs i ,

j

52 C i = 1 , e = T^C v iC i + 52 e ⁰ i ^c i ,

i    ii где Ci, evi, e0i - объемные концентрации, молярные массы, теплоемкости и теплоты образования компонентов газа; si - массовая скорость образования (убыли) компонента газовой фазы; qj - тепловой эффект j-ой независимой реакции, sj - скорость j-й независимой реакции, e - внутренняя энергия газовой смеси.

В силу того, что в данной работе рассматривается модель взаимодействия ударной волны с хвойным лесным массивом, где лесной массив представлен набором экранирующих решеток с малой объемной долей лесных горючих материалов, необходимо в формулах, определяющих межфазное взаимодействие [15, 16] перейти к эффективному значению диаметра частиц d _эфф. Его значение можно найти через значение объемной доли и удельной поверхности S лесных горючих материалов [17, 18]. Так как S = nS₃/V, где S₃ - площадь поверхности элемента лесных горючих материалов; n - количество их элементов в объеме смеси V. Сделаем некоторые преобразования:

S = SnV = ^а 2

где V - объем элемента лесных горючих материалов. Для хвойного леса такой элемент имеет цилиндрическую форму с радиусом r и длиной 1. Тогда:

8_Э   2 nrl + 2 nr 2   2

r << l.

V        nr ² 1        1 ’

Подставляя (4) в (5) имеем:

S — — С . 2 .

С другой стороны, объемную долю и удельную поверхность S частиц можно записать через эффективный радиус частиц:

4пг^<1> = r з п nr•

Тогда связь между d _эфф с радиусом хвоинки r будет иметь вид:

Д>Ф <)>

Для хвойного леса d _эфф= 1 , 5 ■ 10 ~ ³ м, а коэффициент аэродинамического сопротивления частиц С ⁰=О,ОЗ [19]. Определим состав газовой фазы в гетерогенном слое. В результате воздействия излучения (вспышки) на лесной массив, происходит прогрев лесных горючих материалов, что приводит к образованию газообразных продуктов пиролиза. В силу того, что процесс взрыва рассматривается с момента образования

Н.Л. Клиначева, Ю.М. Ковалев объема постоянного давления, то предполагается что в слое распределение параметров газовой фазы равномерно. В данной работе, аналогично [18] будем считать, что газовая фаза состоит из следующих компонентов: N2, O2, С О, CO2, H2O, и в ней происходит одна эффективная химическая реакция окисления окиси углерода СО. Это связано с тем, что концентрации остальных компонентов настолько малы, что не могут повлиять на величину энерговыделения смеси газообразных продуктов пиролиза. Для влажных смесей окиси углерода СО с воздухом, скорость реакции окисления окиси углерода имеет вид [20]:

s = -к о с_слл exp(

E a ₎

RT ^{) ,}

где к 0 = 1 , 4 ■ 10¹² с - 1, E a = 96370 Дж/моль - энергия активации, R = 8 , 31 Дж/молыК - универсальная газовая постоянная.

Численное моделирование рассматриваемой модельной задачи проводилось методом крупных частиц [21], а анализ достоверности полученных результатов проверялся путем уменьшения шагов по пространству. Особенностью численного моделирования является разделение расчетов по процессам. Это объясняется разным временем протекания химических и газодинамических процессов. На каждом временном шаге решаются сначала уравнения химической кинетики, а затем производится расчет газодинамических параметров потока.

В начальный момент времени давление в центре взрыва задавалось равным 2500 атм. Радиус объема постоянного давления в начальный момент времени выбирался таким, чтобы при подходе к слою температура на фронте ударной волны была равной около 1500 К. Такой выбор обусловлен возможностью протекания реакции горения угарного газа. Состав газовой фазы в гетерогенном слое представлен в таблице. Определяющими параметрами задачи являются температура газовой фазы и объемная доля частиц в гетерогенном слое. Первый определяет наличие газообразных продуктов пиролиза, способных к химическим превращениям, а второй - сопротивление движущейся ударной волне. Результаты приведены для значения T/T 0=3, где T 0 температура воздуха вне гетерогенного слоя в начальный момент времени и объемной доли твердой фазы а 2=0.005.

Таблица

Состав газовой фазы

Компонент	N2	O2	CO	CO2	H2O
Концентрация	0,6799	0,199	0,0796	0,00961	0,0319

2. Основные результаты

На рис. 2 представлены изолинии давлений. Видно, что учет энергии реакции окисления окиси углерода приводит к увеличению скорости и интенсивности падающей сферической ударной волны в гетерогенном слое. Кроме того, это приводит к большему росту « ножки » Маха, образованной в результате перехода регулярного

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ отражения к нерегулярному, и предвестника, соединяющего головной фронт ударной волны и часть ударной волны, движущейся по гетерогенному слою.

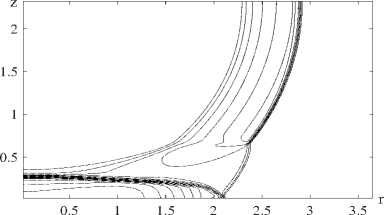
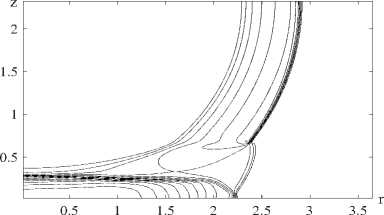
а)

Рис. 2. Изолинии давления: а) без учета химического превращения; б) с учетом химического превращения

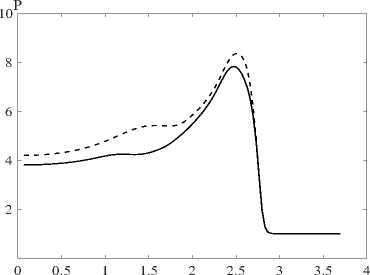
Рис. 3. Распределение давления вдоль поверхности гетерогенного слоя

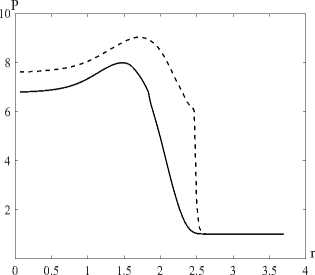
Рис. 4. Распределение давления вдоль стенки

Изменение давления вдоль поверхности гетерогенного слоя и распределение давления вдоль стенки на момент времени t =0,39 показано на рис. 3, 4 (сплошная линия - без учета химического превращения, пунктирная - с учетом химического превращения).

Таким образом, в результате численного исследования показано, что учет химического превращения приводит к увеличению интенсивности и скорости ударной волны, распространяющейся по гетерогенному слою. Следовательно, при рассмотрении задач о воздействии ударных волн, образованных в результате взрыва, на лесные массивы необходимо учитывать энергию химических реакций. Это позволит дать более реальную оценку воздействия взрывной волны на лесной массив.

Н.Л. Клиначева, Ю.М. Ковалев