Взрывной генератор высокоскоростных твердых частиц

Последние десятилетия характеризуются увеличением концентрации техногенных загрязнений околоземного космического пространства, которые негативно влияют на работоспособность элементов конструкций летательных аппаратов.

С целью исследования влияния техногенных частиц на характеристики элементов конструкций космических аппаратов (КА) создаются различные типы ускорителей (электростатических, электромагнитных, взрывных и т. д.).

Наиболее эффективным инструментарием таких исследований является использование метеорологических ракет с установлением на их головных частях научной аппаратуры регистрации потоков высокоскоростных твердых частиц, инициируемых ускорителем взрывного типа [1–4].

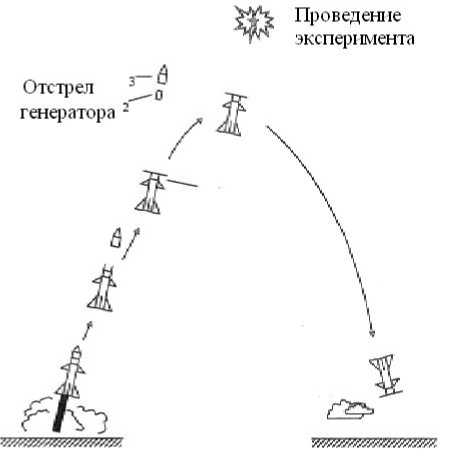
Рис. 1. Схема проведения ракетного эксперимента: 1 – приборный отсек с диагностической аппаратурой; 2 – генератор; 3 – отделяемый модуль

Схема такого эксперимента показана на рис. 1 и включает доставку взрывного генератора частиц и средств диагностики на заданную высоту, отделение и удаление генератора от диагностического отсека ракеты, срабатывание генератора, работу измерительных средств и аппаратуру передачи данных результатов измерений по телеметрическому каналу на Землю.

Указанный метод воздействия потоков частиц на космический аппарат требует изучения характеристик взрывного генератора (распределение частиц в потоке по скоростям и размерам). Исследование характеристик таких генераторов в лабораторных условиях требует использования вакуумной камеры больших размеров специальной конструкции [1].

Из числа возможных способов генерации потоков мелкодисперсных частиц для ракетных экспериментов был выбран наиболее простой взрывной способ, который должен был обеспечивать потоки со скоростями 5–10 км/с, характерными для взаимодействия с КА [2]. Для имитации антропогенного загрязнения использован широко применяющийся дешевый порошок алюминия со средним размером частиц 5–10 мкм. Следует отметить, что алюминий, как и его соединения, в частности окислы, является одним из распространенных компонентов загрязнения околоземного пространства. Были разработаны два типа генераторов. В первом из них порошок замешивался в состав взрывчатого вещества. Скорость частиц, ускоряемых таким генератором, должна была составлять (по результатам лабораторных исследований) в среднем 3–5 км/с. Во втором типе генератора для повышения скорости до ~ 10 км/с использовался принцип метания частиц, при котором упаковка частиц накладывалась на заряд чистого ВВ.

Рассмотрим модель взрывного источника потоков пылевых частиц. Не претендуя на строгую постановку, решим задачу ускорения пылевой частицы в процессе расширения образующегося при взрыве газа. Пусть в момент времени t = t Q имеется сферически симметричный газовый сгусток с плотностью р , радиуса R q , граница которого движется со скоростью U q = const. Для простоты расчетов профиль плотности по сгустку берем постоянным; профиль скорости по сгустку — линейным. Плотность р газа падает по кубическому закону

П — ke ² ^ n ¹² + П = 0                           (2)

с начальными условиями У = 0, n (0) = У о ,

П '^(Q) = ^— У о + V ⁰.

U ₀

Обозначим U = n . Тогда уравнение (2) преобразуется к уравнению Бернулли относительно переменных U и У :

U ' + U — ke ^^У = 0 .

Начальные данные: У = 0, U (0) = — y Q + V 4 q / U q ; делая замену z = 1/ U , получаем линейное уравнение 1-го порядка:

z + z — ke 2 ^У = 0                               (3)

с начальными данными

Р = Ро

t o

t

В момент t = t q частица находится на границе сгустка и имеет начальную радиальную скорость U ₀. Сила давления газа направлена по радиусу, так что частица ускоряется в строго радиальном направлении. Пылевая частица считается сферической. В соответствии с принятой моделью уравнение Ньютона запишется в виде

d2r тЧ —у = Ро dt2

to

t

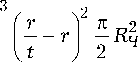
где t – текущее время; r – координата частицы; m_Ч – масса частицы; R_Ч – радиус частицы.

Начальные условия для уравнения (1) таковы: при t = t q r (0) = TQ , r (0) = Vr Q .

Введем переменные: y = r / R q , x = t / t q , где R q = U 0 t o — начальный радиус газового облака ВВ. Тогда уравнение (1) можно записать в виде

"

y

= k

y

x

—

y

где

k =

R ²

2 Р 0 ⁰ t 0 ²       t 0 ²

R ₀ 2 m

n R 4 .

Начальные условия: x = 1, y = y Q , y (1) = V 4 q / U q .

Если учесть, что m = ³р 4 R 4 ( Р Ч — плотность частицы), то

K = 3 ^р о R Q = ³ m о I R 4 | 8 р ч R 4  8 т Ч V R q J

.

Делая замену y = x пУ , У = ln x , получим уравнение

У = о,

z (0) =

^— У о

V Ч 0 .

U 0

Как известно, решение уравнения (3) имеет

вид

z ( У ) = e

где

— F

(

^— У о V

+ V 4 о

U 0

Ч           )

— kJ e—Fe—24 d У о

7

У

F ( У ) = J d У = У . Таким образом, 0

z ( У ) = e ^У

z ( У ) = e ^У

(

^— У о

V Ч 0

U 0

У

— k J e 3^d d У

Г 1

V Ч 0 ^y 0 ⁺

U ₀

— k (1 — e—3)

Так как У = ln x , то

z ( У ) = ee¹

U ( x ) =

Г ¹

V Ч 0

^y Q +ТГ

V ^U о

k

—

—

;

x

Г 1

V_{Ч 0}

^{— y} 0 ⁺

U ₀

—

k

1-

1 x ³

.

dn    dn

Так как —^7 = x —j— ,

d У

то

x

П ( x ) = J

xdx

k

—

3 Г k x

—

.

V Ч 0

^{— y} o ⁺

U ₀

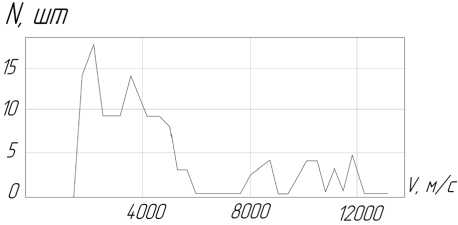
Рис. 2. Экспериментальное распределение скоростей частиц

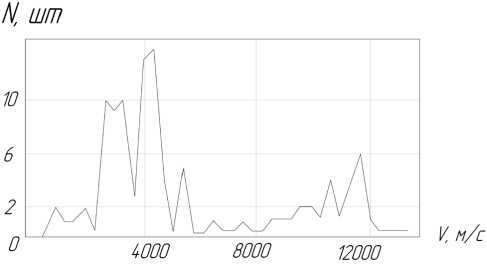
Рис. 3. Расчетное распределение скоростей частиц на расстоянии 30 м от источника

Рис. 4. Многопараметрический преобразователь потоков частиц

Обозначим

к 3

= a , 3

k

_____1_____= c3

V40

— У о + Ч

⁰    U 0

При x ^ да асимптотическое значение скорости пылевой частицы будет равно

'

y да

тогда (4)

П ( x ) = -12- J

можно представить в виде x

xdx

a ³ -

:; ^{+ y} 0 . x ³

c ²

+ -j=-

V 3 a

c

Используя таблицы интегралов, получим:

П ( x ) = "2 c ²

1 ln a 2 ⁺ acx ⁺ ( cx ) ² ^ ( a — c ) ^{2 6} a _к a ² + ac + c ² _? ( a — ac ) ²

+

1ln

6 a

arctg

. 1 f и _U + a 2 cxcx + a + — arctg ^=— arctg -j=—

V3 a к       a V3           a^3

^{+ y}0 .

Таким образом, закон движения частицы имеет

вид

У ⁽ x ) =

= x

1 c ²

1 , ^f a ² + acx + ( cx )² ln

6 a к a² + ac + c² J

^{( a — c ) 2}

( a — ac ) ²

+

. 1 f и _U + a 2 cxcx + a + _r arctg -j= — arctg y=—

V3 a к       a V3           a VS

^{+ y} 0

Скорость частицы определиться из (5):

'              ¹

У ( x ) = -2

c ²

1 ln a ² + acx + ( cx ) ² ^ ( a — c ) ^{2 6 a} _к a ² + ac + c ² _? ( a — ac ) ²

+

. 1 f и _U + a     .2 cx + a

+ ,- I arctg -;=— arctg ;=—

V3 a к        a-J3           a V3

^{+ y} 0 ⁺

a

—

x ³ .

^{( a — c} )

a + ac + c

2 c + a a V3

—

n

+

^{+ y} 0 .

Преобразуем выражение (6):

' 1

y Ю = ^y 0     2

3 ac ²

+ V3

n

2 — arctg

ln

V ( a + c )² — ac

к

c — a

2 c + a k a V3 ^J

При k ^ да (масса пылинки т ч ^ да ) параметры а ^ да , с ^ да . Вычисляя предел в (7), получим у _да ^ 1. При к ^ 0 (масса пылинки т ч ^ да ), а ^ 0, с ^ 0, у _да ^ 0. Таким образом, чем меньше масса, тем больше скорость частицы.

Если в стадии инерционного разлета газообразных продуктов взрывчатого вещества принять R y = 1 м, р = 1 кг / м³, то для пылинки радиуса R 4 = 10⁶ м, плотности р = 1 кг / м³ = 5, параметр к = 375. Тогда a = ( k / 3)³ = 5, с = 5,018

и скорость у _да = 0,98. Для частицы R 4 = 10 м = = 10 мкм скорость у _да = 0,893.

Таким образом, в рамках данной модели ускорения пылевых частиц с использованием ВВ

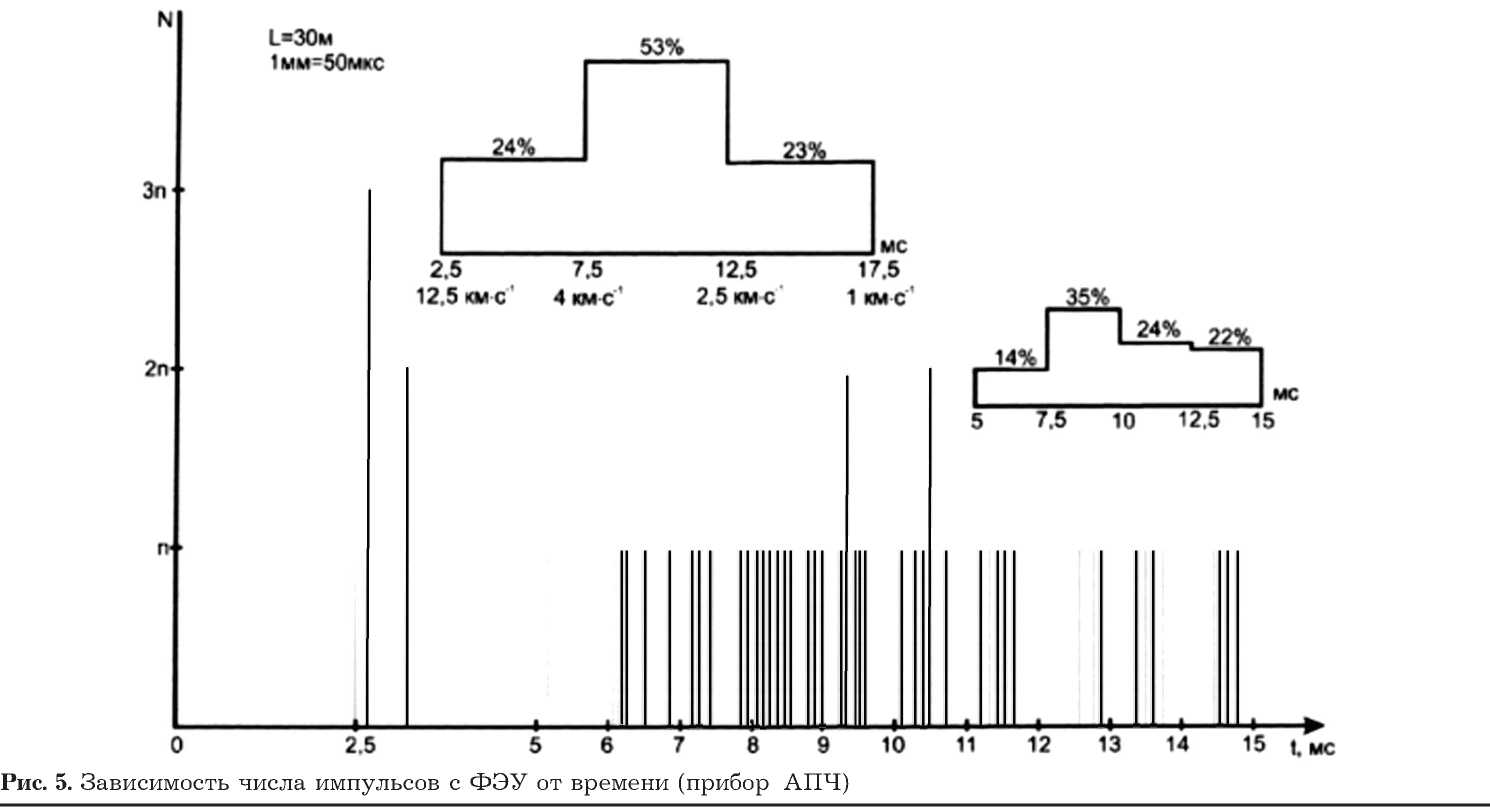
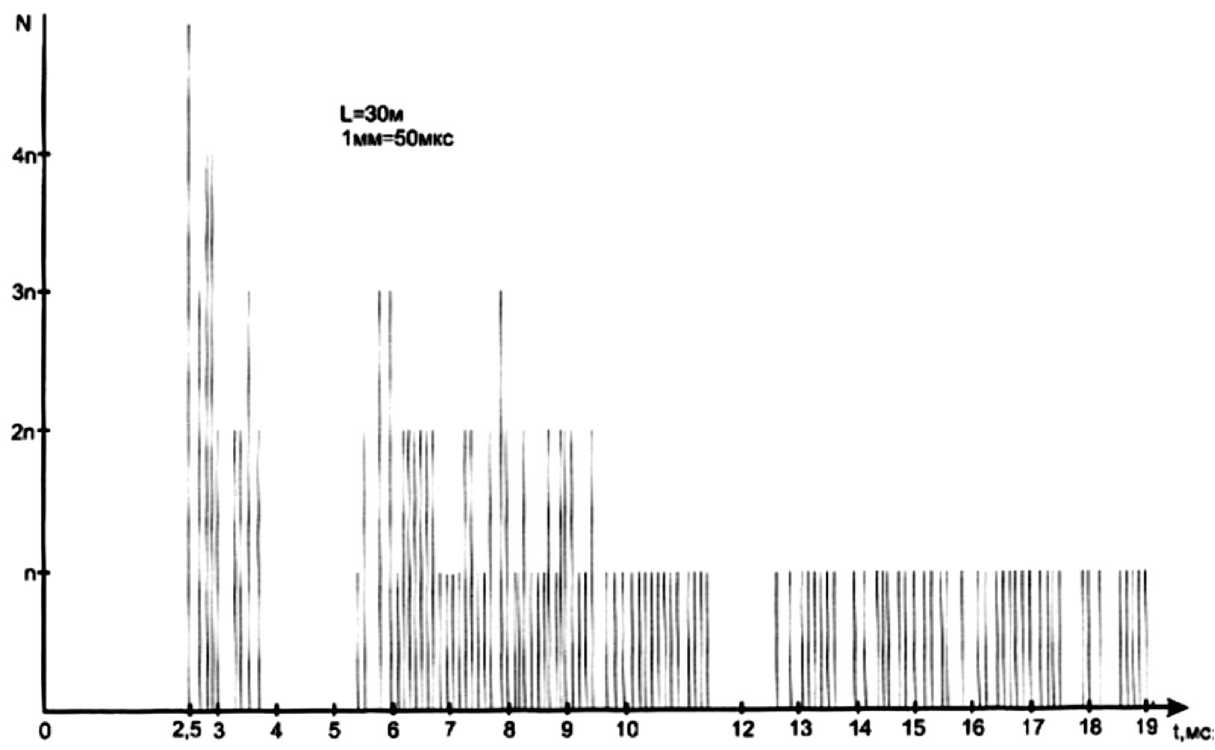
Рис. 6. Зависимость числа импульсов с ВЭУ от времени (прибор АПЧ)

Таблица

R , мкм	Ur 0	a	c	U ∞
	0	5	5,013	0,98
1	0,5	5	5,026	0,982
	0,9	5	5,130	0,987
	0	2,32	2,38	0,87
10	0,5	2,32	2,43	0,893
	0,9	2,32	2,82	0,946
	0	1,077	1,31	0,46
100	0,5	1,077	1,48	0,654
	0,9	1,077	2,24	0,91
	0	0,5	1,04	0,0847
1000	0,5	0,5	1,285	0,522
	0,9	0,5	2,163	0,9009

Т. 19, № 1

скорость пылинки слабо зависит от ее массы. В этом случае следует ожидать компактные потоки пылевых частиц с высокой плотностью потока. Однако скорость частиц сильно зависит от начальных условий при t = t ₀, так как в общем случае в процессе образования взрывного облака частицы могут оказаться в любой точке расширяющегося газового облака. В таблице даны значения скоростей в зависимости от радиуса частицы при различных значениях величин а и с .

На рис. 2 и рис. 3 показаны соответственно расчетное и экспериментальное распределение потока частиц по скоростям. Эксперименты выполнены с помощью ракет, по схеме, показанной на рис. 1, а экспериментальные данные о характеристиках потока частиц получены с помощью разработанного нами многопараметрического прибора АПЧ-1 (рис. 4).

Из рис. 2 и 3 видно, что теоретическое и экспериментальное распределения на качественном уровне совпадают.

Аппаратура АПЧ-1 состояла из люминесцентного, ионизационного и фотоэлектрического датчиков и блока обработки информации [3; 4].

На рис. 5 и 6 соответственно приведены экспериментальные данные гистограмм с фотоэлектронного умножителя люминесцентного датчика и с ионизационного датчика. Из рисунков видно, какой процент частиц соответствует диапазону скоростей.

Потоки частиц получались с помощью специального разработанных генераторов взрывного типа [1], и создаваемые ими частицы воздействовали на элементы конструкций космических аппаратов, установленные на головной части ракеты [3].

Датчики позволяют измерить потоки частиц 10 см ^{- 2} ⋅ с ^{- 1}. Быстродействие аппаратуры обработки информации обеспечивает работу датчиков в счетном режиме.

В реальном масштабе времени отложены частоты появления сигнальных импульсов. В соответствии с временной диаграммой прибор включался через 2,5 мс после светового сигнала, возникающего при подрыве заряда ВВ. Полученная плотность потока частиц соответствует максимальной частоте импульсов 1000 час / (см² ⋅ с) для люминесцентного датчика и 10000 час / (см² ⋅ с) для ионизационного датчика. Такой разброс результатов объясняется более высокой чувствительностью ионизационного датчика по сравнению с люминесцентным.

Наиболее вероятная скорость в исследуемом потоке лежит в интервале от 2,5 до 4 км/с, что соответствует ожидаемым скоростям при моделировании потоков с помощью ВВ. Плотность потока частиц, соответствующая максимальной 4      - 2 - 1

частоте импульсов, не превышает 10 см ⋅ с для люминесцентного датчика и 10⁵ см ^{- 2} ⋅ с ^{- 1} для ионизационного датчика.

Такой разброс результатов по двум датчикам, возможно, объясняется тем, что чувствительность ионизационного датчика на порядок превышает чувствительность люминесцентного, потому что площадь чувствительной поверхности ионизационного датчика в 10 раз меньше площади люминесцентного. Так как скорость пылевых частиц слабо зависит от массы, а импульс с люминесцентного датчика пропорционален кинетической энергии налетающей частицы, то, по-видимому, большая часть мелких пылевых частиц не регистрировалась люминесцентным датчиком. Таким образом, в качестве правдоподобной величины можно принять величину максимальной плотности потока порядка 5     - 2 - 1

• 10 см ⋅ с .

Результаты проведенных исследований с помощью ракет показали, что к настоящему времени информация о взаимодействии потоков высокоскоростных пылевых частиц с веществом малочисленна. Большое количество работ посвящено взаимодействию одиночных частиц с веществом. Физические процессы одиночных частиц и потоков не всегда эквивалентны. В данной работе рассмотрен вопрос формулирования основных характеристик потока пылевых частиц и выведен критерий для величины плотности потоков, при которой неэквивалентность физических процессов носит не только интегральный, но и дифференциальный характер. Для моделирования таких потоков необходимо использование специальных средств. Наиболее эффективным устройством для создания таких потоков пылевых частиц является электромагнитный ускоритель для разгона контейнеров с пылевыми частицами.

Проведенный натурный эксперимент с использованием источников пылевых потоков взрывного типа показал, что разработанный прибор АПЧ-1 позволяет регистрировать потоки частиц в диапазоне j = 10–10⁶ см ^{- 2} ⋅ с ^{- 1} и V = 0,5–15 км/с.

Проведенный эксперимент также показал, что плотность потока в максимуме распределения составила j = 10⁵ см ^{- 2} ⋅ с ^{- 1}, а скорость V = 3 км/с.

Разработанная модель источника потоков пылевых частиц взрывного типа, а также информация, полученная с прибора АПЧ-1, позволят решить задачу перехода от характеристик потока к основным характеристикам источника.

Спроектированный прибор АПЧ-1 с совместным использованием различных эффектов дает возможность определить не только характеристики потоков, но и параметры одиночных частиц (массу, скорость) как в натурных, так и лабораторных условиях.

Выбор и совмещение методов измерения характеристик потоков пылевых частиц являются результатом исследования известных перспективных методов измерения.