Взвешенная вероятностная оценка бизнес-процесса на основе формализмов цепей Маркова

Введение. При управлении и модернизации бизнес-процессов актуальной является задача получения обобщенных характеристик, оценивающих эффективность их функционирования [1; 2]. Единого, сложившегося подхода к решению этой задачи не выработано. В данной работе предлагается подход, основанный на совместном использовании методологии ARIS ЕРС и формализмов цепей Маркова. Метод дополняет и отчасти заменяет процедуры имитационного моделирования бизнес-процессов, предоставляя четкий и однозначный ответ о стоимости и времени выполнения бизнес-процесса на основе его статистических характеристик, а также позволяет оценить изменения временных и стоимостных характеристик процесса в результате совершенствования бизнес-процесса.

Данная работа начинается изложением основных положений формализма конечных цепей Маркова применительно к описанию бизнес-процессов. Затем на примере условного бизнес-процесса излагается методика оценки временных и стоимостных характеристик процесса путем взвешивания вероятностей пребывания в заданных состояниях процесса. И наконец эта же задача решается на основе оценки среднего числа пребываний про цесса в заданных состояниях. Показано, что эти два метода дают близкие результаты.

Формальная модель бизнес-процессов. Представляет собой динамическую систему, находящуюся в каждый из моментов t в одном из п состояний множества S = {/?,,...,5^}, t_k еТ, гдеТ - множество моментов времени, в которые рассматривается система [3; 4; 5]. Переменная t представляет собой шаг выполнения процесса и не обязательно связана с календарным временем.

Состояния изменяются со временем случайным образом. Это изменение определяется матрицей переходных вероятностей

P(/J = k(/J||. (1)

Каждый элемент матрицы р_е Qffi,j = 1,..., п показывает вероятность того, что если система в момент t_k находилась в состоянии S,, то в момент t_k+1 она окажется в состоянии Sj: p_tj Q_k ) = Pr {S' Q_k+1) = S_y IS(t_k) = S,}.

Каждая строчка матрицы P соответствует состоянию, в котором процесс находится на данном шаге, а каждый столбец - состоянию, в которое переходит процесс на следующем шаге. Переходы во все возможные состоя- ния (в том числе в себя) образуют полную группу событий, поэтому Т^Ру О = 1 для всех z = 1,п , tk е Т.

7=1

В данной работе мы предполагаем, что вероятности не зависят от времени, т. е. цепь Маркова однородна, матрица Р является числовой. В отношении бизнес-процес-са с установившейся технологией исполнения это ограничение представляется обоснованным.

Вектор-строка 26(4) = [^ (4), •••’ xn (4)] описывает распределение вероятностей нахождения системы в соответствующих состояниях в момент tk, то есть хр^ - это вероятность того, что в момент t система находится в состоянии S.. При этом 21Л Qk^ = 1, tk е Т. Пересчет распределения вероятностей на следующем шаге производится по формуле

ХМ = Х^Р. (2)

Должно быть также задано начальное условие: X (/₀) = X_Q, которое определяет состояние процесса на начальном шаге выполнения бизнес-процесса.

Вычисляя последовательно X^t), X(t₂), ..., X(t_k ), мы можем получить вероятностный прогноз развития состояний бизнес-системы в процессе ее функционирования.

Множество состояний 5 в рассматриваемом случае подразделяется на множество невозвратных состояний 5¹ и множество поглощающих состояний X. Состояния, относящиеся к множеству S², соответствуют завершению выполнения бизнес-процесса и не влияют на его трудоемкость. Поэтому исключив из матрицы Р строки и столбцы, соответствующие состояниям из S², и обозначив оставшуюся матрицу О. можно вычислить так называемую фундаментальную матрицу цепи Маркова:

N = Q-gy\ (3)

где I - единичная матрица размерности т , где т - количество состояний невозвратного множества.

Каждый элемент п матрицы N представляет собой среднее число пребываний процесса в состоянии 5. при старте из состояния S., причем S. .S^S'.

Описание бизнес-процессов. В данной работе выбрана методология ARIS ЕРС [6; 7; 8], которая, впрочем, безболезненно может быть заменена на IDEF3 или UML StateChart Diagram, словом - на любую нотацию, предназначенную для описания сценариев выполнения бизнес-процессов.

При этом связи модели ЕРС будут соответствовать переходам между состояниями цепи Маркова. В тех случаях, когда связь безальтернативна, вероятность соответствующего перехода будет единичной. Тогда же, когда процесс предполагает ветвление, вероятность перехода сопоставляется с вероятностями срабатывания соответствующих связей. При этом условие равенства единице суммы переходных вероятностей по строке матрицы переходных вероятностей соблюдается, поскольку в ЕРС на вероятность связей также накладывается условие равенства единице суммы вероятностей связей после ветвления.

Рассмотрим сопоставление на примере условного бизнес-процесса производства и сбыта заказных изделий (см. рисунок).

Определим состав элементов модели бизнес-процесса, их характеристики и соответствующие элементам состояния цепи Маркова (табл. 1).

В соответствии с приведенной моделью бизнес-процессов можно построить матрицу переходных вероятностей цепи Маркова.

Полученная матрица переходных вероятностей позволяет получить по формуле (2) распределение вероятностей нахождения системы в различных состояниях на каждом следующем шаге.

Значения вектора АД). задающего распределение вероятностей перед началом функционирования системы, можно определить из следующих соображений:

• -    вероятности состояний, соответствующие стартовым событиям, принимают значения, соответствующие вероятности наступления данного события на старте процесса; по очевидным причинам сумма этих вероятностей должна быть равна единице;

Таблица 1

Состав элементов модели бизнес-процессов и их сопоставление с событиями цепи Маркова

Наименование объекта модели	Тип объекта модели ЕРС	Среднее время выполнения, ч	Средняя стоимость выполнения, руб.	Состояние цепи Маркова
Заказ на нестандартное изделие	Событие	0,00	0,00	51
Заказ на стандартное изделие	Событие	0,00	0,00	52
Проектирование изделия	Процесс	16,00	10 000,00	53
Проект выполнен	Событие	0,00	0,00	54
XOR rale 1	Перекресток	0,00	0,00	Ss
XOR rale 2	Перекресток	0,00	0,00	s6
Изготовление изделия	Процесс	8,00	5 000,00	s-
Изделие некондиционное	Событие	0,00	0,00	S8
XOR rale 3	Перекресток	0,00	0,00	s9
XOR rale 4	Перекресток	0,00	0,00	5io
Клиент потребовал доставить товар на дом	Событие	0,00	0,00	5ii
Доставка клиенту	Процесс	4,00	1 000,00	512
Заказ доставлен	Событие	0,00	0,00	5i3
Клиент решил забрать товар в магазине	Событие	0,00	0,00	514
Передача клиенту в магазине	Процесс	16,00	500,00	515
Заказ получен	Событие	0,00	0,00	5i6

- все остальные вероятности состояний должны быть равны нулю - ни в каком состоянии, кроме стартового, система на старте находиться не может.

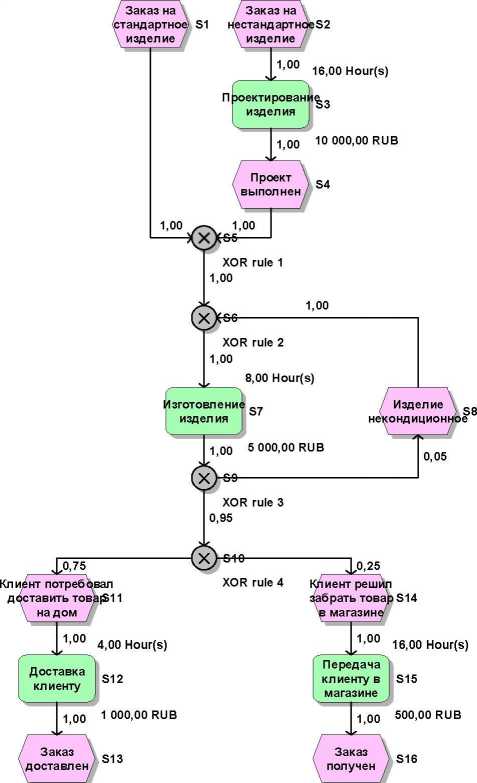
Модель бизнес-процесса в нотацииЛТЖ

В приведенном примере примем вероятность поступления заказа на стандартное изделие равной 0.8. а на нестандартное - 0,2.

Количество шагов определяется по стандартному правилу. когда расчет останавливается после достижения суммой вероятностей нахождения системы в поглощающих состояниях значения 0.95. В приведенном примере это соответствует 11 шагу расчета.

Полученный расчет позволяет получить взвешенную оценку стоимости и времени выполнения процесса.

Для этого введем значения С. и Г., означающие соответственно среднюю стоимость выполнения и среднее время выполнения каждого из состояний (см. табл. 1). Для всех состояний, кроме соответствующих бизнес-про-цессам. они равны нулю. Взвешивание произведем по х" - суммарным значениям вероятности нахождения системы в каждом состоянии, вычисляющимся по формуле:

м

^^^М-(4)

где М- количество шагов расчета.

Далее рассчитываем взвешенное время выполнения Т и взвешенную стоимость выполнения процесса ( '.

Т = ^ф.(5)

с=^Х(

/=1

Полученные формулы позволяют оценить воздействие на бизнес-систему, во-первых, внешних условий -в приведенном примере они моделируются соотношением стандартных и нестандартных заказов; во-вторых -изменения внутреннего качества системы - в приведенном примере это задается как прямой стоимостью и временем выполнения входящих в бизнес-процесс функций, так и изменением соотношения кондиционных и некондиционных изделий, что описывается изменением соответствующих переходных вероятностей.

Подобный подход применяется при оценке инвестиционных рисков [6; 9], поэтому применение стоимостной и временной оценки процесса, взвешенной на вероятность обращения к каждой из функций этого процесса представляется обоснованной.

Для иллюстрации проведем несколько численных экспериментов. Исследуем взвешенную стоимость и взвешенное время выполнения процесса, приведенного в примере при варьировании параметров внешней среды - соотношения стандартных и нестандартных заказов как 50/50, 75/25 и 90/10, а также при варьировании качества работы системы - процент брака 10 %, 20 % и 30 %.

Расчет проведем по формулам (2), (4), (5) и (6) (табл. 2).

Оценка бизнес процесса на основе значений фундаментальной матрицы цепи Маркова. Приведем фундаментальную матрицу для рассматриваемого примера, рассчитанную по формуле (3) (табл. 3).

Таблица 2

Взвешенные оценки процесса Т и С при варьировании параметров внутренней и внешней среды предприятия

Вероятность брака Показатель: Соотношение стандартные/ нестандартные 50/50 75/25 90/10 10% Т 23,495 19,653 17,347 С 11 376,875 8 896,563 7 408,375 20% Т 24,080 20,360 18,128 С 11 970,000 9 505,000 8 026,000 30% Т 24,755 21,123 18,943 С 12 654,375 10 200,313 8 727,875 ipUXXJX XXVXXVj./ "1V11 j_/Vl^C4

формул нету в файле

Поскольку каждый элемент п матрицы N представляет собой среднее число пребываний процесса в состоянии 5. при старте из состояния S., то можно использовать значения этих элементов для получения взвешенной оценки времени и стоимости выполнения процесса. Строка к фундаментальной матрицы позволяет оценить время Т_к и стоимость С_к выполнения процесса при запуска из к-то состояния по следующим формулам:

Т.^п^,            (7)

Z=1

Q=fXQ.           (8)

М

Тогда взвешенное время Т и стоимость С всего бизнес-процесса может быть рассчитана путем взвешивания Т_к и С_к на р_к - вероятность запуска процесса с к-то состояния (процесса, события).

f=ip_tf_k,             (9)

£=1

с = Т,р_кс_к.              (Ю)

В приведенном примере ^соответствует вероятностям стартовых событий («Заказ на стандартное изделие» и «Заказ на нестандартное изделие»). Стартовые вероятности остальных состояний равны нулю.

Для иллюстрации проведем несколько численных экспериментов, аналогично тому, как это было сделано для Т и С. Исследуем взвешенную стоимость и взвешенное время выполнения процесса, приведенного в примере при варьировании параметров внешней среды - соотношения стандартных и нестандартных заказов как 50/50, 75/25 и 90/10, а также при варьировании качества работы системы - процент брака 10 %, 20 % и 30 %.

Расчет проведем по формулам (9), (10) (табл. 4).

Сравнение табл. 4 и 6 показывает, что оба способа оценки взвешенной стоимости и времени процессов дают близкие результаты при одинаковых исходных данных. Оба метода верно отражают тенденцию изменения времени и стоимости процесса при изменении внутренней и внешней среды.

На практике предложенные взвешенные оценки Т и С и Т, С могут быть востребованы для сравнительной оценки аналогичных бизнес-процессов двух предприятий (бенчмакинг), а также для оценки последствий внутренних изменений. Так, в приведенном примере можно оценить в деньгах и затраченном времени эффект от мероприятий по повышению качества продукции.

Мы видим, что предложенная методика позволяет оценить поведение системы, исходя из ее вероятностных

Таблица 3

Фундаментальная матрица цепи Маркова для приведенного примера

	5i	52	5з	54	55	56	Sy	s8	s9	5io	511	5[2	514	515
51	1,00	0,00	0,00	0,00	1,00	1,11	1,11	0,00	1,11	1,00	0,75	0,75	0,25	0,25
52	0,00	1,00	1,00	1,00	1,00	1,11	1,11	0,00	1,11	1,00	0,75	0,75	0,25	0,25
53	0,00	0,00	1,00	1,00	1,00	1,11	1,11	0,00	1,11	1,00	0,75	0,75	0,25	0,25
54	0,00	0,00	0,00	1,00	1,00	1,11	1,11	0,00	1,11	1,00	0,75	0,75	0,25	0,25
s5	0,00	0,00	0,00	0,00	1,00	1,11	1,11	0,00	1,11	1,00	0,75	0,75	0,25	0,25
s6	0,00	0,00	0,00	0,00	0,00	1,11	1,11	0,00	1,11	1,00	0,75	0,75	0,25	0,25
Sy	0,00	0,00	0,00	0,00	0,00	0,11	1,11	0,00	1,11	1,00	0,75	0,75	0,25	0,25
S8	0,00	0,00	0,00	0,00	0,00	0,00	0,00	1,00	0,00	0,00	0,00	0,00	0,00	0,00
s9	0,00	0,00	0,00	0,00	0,00	0,11	0,11	0,00	1,11	1,00	0,75	0,75	0,25	0,25
5io	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	1,00	0,75	0,75	0,25	0,25
5ц	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	1,00	1,00	0,00	0,00
512	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	1,00	0,00	0,00
514	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	1,00	1,00
515	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	1,00

Таблица 4

Взвешенные оценки процесса и при варьировании параметров внутренней и внешней среды предприятия

Вероятность брака Показатель Соотношение стандартные/ Нестандартные заказы 50/50 75/25 90/10 10% 23,889 19,889 17,489 1 1430,556 8 930,556 7 430,556 20% 25,000 21,000 18,600 12 125,000 9 625,000 8 125,000 30% 26,429 22,429 20,029 13 017,857 10 517,857 9 017,857 характеристик. Описание системы формируется в виде формальной модели бизнес-процесса, наполненной статистическими характеристиками - временами и стоимостями выполнения функций, вероятностями развития процесса по вариантам. Расчет изменения вероятности пребывания системы в состояниях по шагам, а также среднего числа пребываний в состояниях невозвратного множества позволяет накопить статистику по каждому состоянию, показывающую общее число пребываний процесса в данном состоянии (среднее количество выполнения каждой функции, наступления каждого события). Сумма времен и стоимостей выполнения функций, взвешенная на накопленные таким образом вероятности, позволяет оценить бизнес-процесс. При этом изменение управляемых параметров позволяет оценить изменение стоимости и времени бизнес-процесса при различных состояниях внутренней и внешней среды предприятия. Развитие предложенных методов может состоять в автоматизации процессов построения цепей Маркова и их исследовании по структурным схемам бизнес-процессов.